Efficient allocations in economies with asymmetric information when the realized frequency of types is common knowledge

Abstract

We consider a general economy, where agents have private information about their types. Types can be multidimensional and potentially interdependent. We show that, if the realized frequency of types (the exact number of agents for each type) is common knowledge, then a mechanism exists, which is consistent with truthful revelation of private information and which implements first-best allocations of resources as the unique equilibrium. The result requires the single-crossing property on utility functions and the anonymity of the Pareto correspondence.

1 Introduction

As first shown by Akerlof (1970), Spence (1973) and Rothschild and Stiglitz (1976), hidden-type (adverse selection) problems can have significant consequences in terms of efficiency on economic outcomes. More specifically, incentive compatibility constraints limit the set of feasible allocations that can be attained (see, e.g., Dréze et al. 2008). How are these restrictions relaxed as more information becomes common knowledge? And what is the minimum additional information required for achieving first-best efficiency? These are some of the questions that have emerged in the attempt to better understand the effects of information aggregation on efficiency. Indeed, some early papers by McAfee (1992), Armstrong (1999) and Casella (2002) already point toward this direction.

In this paper, we claim that if the number of agents with the same type is known for all types in a population (in other words, the realized frequency of types is known), then it is possible, under general conditions, to implement first-best allocations as a unique equilibrium. More precisely, we consider an economy with asymmetric information, where each agent has private information about his type. We also assume that: (i) the realized frequency of types is common knowledge, (ii) preferences satisfy the single-crossing property, and (iii) the social choice rule satisfies anonymity. Given these conditions, we show that it is possible to construct a mechanism which has a unique equilibrium, where all agents reveal their type truthfully and they receive a first-best allocation.

The result is interesting because we examine an asymmetric information problem which is situated in between the problem of Maskin (1999) (in which all agents know the state of the world but the mechanism designer does not know it) and the classic adverse selection (in which each agent knows only his own type and the mechanism designer knows the ex ante distribution of types). The intuition behind the result is that, if the realized frequency of types is known, then one can aggregate the messages that all agents are sending out and uncover any misreport(s), even if the identity of the liar is not known. That is, appropriately designed punishments for lying can induce agents to reveal their information truthfully. We talk about appropriately designed punishments, because one of the features of our mechanism is that punishments must not be too harsh. If the punishment when a lie is detected is too severe, then some agents may deliberately lie about their type in order to force other agents to also do so. The lies cancel out at the aggregate level and the former agents “steal” the allocations of the latter, who are forced to lie under the fear of the extreme punishments. This can lead to coordination failures and multiplicity of equilibria. Therefore, uniqueness of the equilibrium requires a careful construction of the off-the-equilibrium-path allocations when lies are detected. We show that such punishments exist when the indifference curves satisfy the single-crossing property.

Furthermore, our mechanism can be useful in addressing real-world problems when agents’ individual characteristics (types) are privately known, but the central authorities have good knowledge of the relevant aggregate numbers. For example, a government may know the aggregate output (income) and the productivity in each sector but not the productivity of each individual agent. In such a case, the government can employ our mechanism and taxes/subsidies to redistribute income without any losses in terms of efficiency. Another example is the identification of the amount of air pollution by each factory and the imposition of the corresponding penalty without direct inspection. For this result, our mechanism requires knowledge of the aggregate air pollution and the aggregate number of the machines used along with the machine specifications determining the emission of air pollutants.

The most closely related paper to ours is Piketty (1993) which also assumes that the realized distribution of types is common knowledge. Piketty considers the classical taxation problem of Mirrlees (1971) and proposes a mechanism which allows the government to implement any first-best efficient allocation. Our model differs from Piketty in several respects: (i) Piketty considers only two private goods, while we allow for any finite number of goods (some of which could be public). (ii) We consider multidimensional asymmetric information instead of unidimensional. (iii) We allow for a more general feasibility set.

Jackson and Sonnnenschein (2007) consider an economy where agents play multiple copies of the same game at the same time and their types are independently distributed across games. They allow for mechanisms, which “budget” the number of times that an agent claims to be of a certain type. If the number of parallel games becomes very large, then all the Bayes-Nash equilibria of these mechanisms converge to first-best allocations. Our model is different from theirs, because we do not require multiple games to be played at the same time, but we impose a stronger assumption on what is common knowledge.

Sun and Yannelis (2007a, (2008) show how incentive compatibility constraints can be overcome and first-best achieved in economies with private information and atomless agents. This efficiency result requires that the agents’ private signals be conditionally independent (given the true state of nature) and utility functions and endowments be type independent. Also, this result does not hold for economies with asymmetric information and a fixed finite number of agents.

McLean and Postlewaite (2002, (2004) consider efficient mechanisms in economies with interdependent values. The state of the world is unknown to all agents, but each individual receives a noisy private signal about the state. They show that when signals are sufficiently correlated with the state of the world and each agent has small informational size (in the sense that his signal does not contain additional information about the state of the world when the signals of all the other agents are taken into account), then their mechanism implements allocations arbitrarily close to first-best allocations. However, in the model of McLean and Postlewaite, when private signals are perfectly correlated, all agents learn not only their own type but also the type of all other agents. That is, in the limit, the framework of McLean and Postlewaite is one of complete information. In contrast, in our setting agents know, at most, the realized frequency of types.¹

VCG mechanisms (Vickrey 1961; Clarke 1971; Groves 1973) are often reference points in terms of results on efficiency. With respect to these mechanisms, our paper is more general as they assume quasi-linear preferences, while we allow for quasi-concave utility functions. Moreover, these papers show that the respective mechanisms that they examine produce truth-telling equilibria, but they do not examine whether other equilibria, non-truth-telling, exist. In contrast, we consider this possibility and show that the truth-telling equilibrium of our mechanism is unique.

Our paper is also related to the auctions literature with interdependent types. In this context, Crémer and McLean (1985) and Perry and Reny (2002, (2005) show the existence of efficient auctions when types are interdependent. Crémer and McLean, however, require quasi-linear preferences, while we do not. Perry and Reny are closer to our result since they also assume that the single-crossing property holds. Nonetheless, our main focus is the uniqueness of the equilibrium, an issue which, as with the VCG literature, is not studied in these papers.

Rustichini et al. (1994) show that the inefficiency of trade between buyers and sellers of a good, who are privately informed about their preferences, rapidly decreases with the number of agents involved in the two sides of the market and in the limit it reaches zero. Effectively, the paper examines the issue of convergence to the competitive equilibrium as the number of agents increases. However, their model is limited to private values problems and hence it can be seen as a special case of our formulation.

Following this direction of research, subsequent papers have examined the existence and efficiency of equilibria in economies with asymmetric information when: (i) there is a continuum of agents (Sun and Yannelis 2007b), (ii) there are infinitely many commodities (Podczeck and Yannelis 2008), (iii) there is an infinite number of agents and aggregate uncertainty (Qiao et al. 2016), (iv) there is a mix of “small” and “large” agents (Pesce 2010), and (v) there are more private goods than states of nature (Correia-da-Silva and Hervés-Beloso 2014). As in Rustichini et al. (1994), these papers restrict their focus to satisfying incentive compatibility constraints, while we are interested in full implementation.

More recently, the papers by Mezzetti (2004) and Ausubel (2004, (2006) examine the issues of efficient implementation under interdependent valuations and independently distributed types. However, they also assume that agents’ preferences are quasi-linear with respect to the transfers they receive, whereas in our model utility may not be transferable. Moreover, the mechanisms proposed in these papers may generate multiple equilibria (in most of which truth-telling is violated), while we are interested in a mechanism which has a unique truth-telling equilibrium.

Finally, several recent papers examine efficient mechanism design in dynamic settings. The most notable papers in this category are the papers by Battaglini (2005), Athey and Segal (2007), Gershkov and Moldovanu (2009), Bergemann and Välimäki (2010), Pavan et al. (2014), Athey and Segal (2013) and Escobar and Toikka (2013). Our paper differs significantly from these papers. We assume that types are drawn only once and the realized distribution of types becomes common knowledge subsequently, while they assume that agents’ type evolves over time according to a stochastic process which is common knowledge. On the other hand, we also use a multistage mechanism in order to induce truthful reporting. As a result, even though agents’ private information does not change in the various stages, their incentive to report truthfully changes according to the information they learn from the previous stages, similarly to the dynamic mechanism design literature.

2 An example: Spence (1973)

First we demonstrate how the knowledge of the realized frequency of types can be used to implement first-best allocations as a unique equilibrium by applying the main idea to the classic paper by Spence (1973). The economy consists of two types of workers. Type 1 has low productivity $\underline{a}$, and its proportion of the population is $q_1$. Type 2 has high productivity $\overline{a}~,~ (\overline{a}>\underline{a})$, and its proportion of the population is $1-q_1$.² Acquiring y units of education costs $y /\underline{a}$ for type 1 and $y /\overline{a}$ for type 2. Productivity parameters are private information, and firms hire workers according to a wage schedule, based on verifiable educational attainment. The payoff for an individual is the value of his wage minus the educational cost and for a firm the productivity parameter minus the wage.

Spence argues that agents will acquire education (which does not increase productivity in his model) in order to signal their productivity to firms. In equilibrium, the wage schedules are such that high-productivity workers acquire some education and credibly signal their type, while low-productivity workers acquire no education, and firms correctly infer that they are of low productivity. The education acquired by type 2 is a deadweight loss, but necessary for credible signaling.

Fig. 1

Application to Spence (1973)

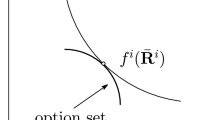
Assume that the total population is N. Then $Nq_1$ is the total number of agents of type 1, and $N(1-q_1)$ is the total number of agents of type 2. Given this, the following mechanism can separate types without any agent incurring educational costs in equilibrium. Let all workers report their type. If the number of agents who report type 1 and 2 is $Nq_1$ and $N(1-q_1)$, respectively, then agents who report type 1 receive wage $w_{1}=\underline{a}$ and zero education (contract $\alpha _1^{FB}$ in Fig. 1) and those who report type 2 receive wage $w_{2}=\overline{a}$ and zero education (contract $\alpha _2^{FB}$ in Fig. 1). In any other case, where the reported number of types does not match their population size, those who report type 1 receive $w_{1} =\underline{a}$ and those who report type 2, are asked to undertake one unit of education and receive $w_{2}=\underline{a}+\epsilon$, with $\frac{1}{\overline{a}} ~<~\epsilon ~<~ \frac{1}{\underline{a}}$ (recall that a unit of education costs $\frac{1}{\overline{a}}$ for high-productivity workers and $\frac{1}{\underline{a}}$ for low-productivity workers).

The above mechanism fully implements the first-best allocations in this economy. First, consider the strategies of type 2. It is clear that, irrespective of the reports of the other agents, it is a strictly dominant strategy for him to report his type truthfully. This is because, when everybody else reports truthfully, type 2 prefers to report truthfully as well (then his payoff is $\overline{a}$) than to misreport his type (then his payoff is $\underline{a}$), given that $\overline{a}>\underline{a}$. Similarly, if someone else lies, type 2 prefers to report truthfully and receive a payoff of $\underline{a}+\epsilon -\frac{1}{\overline{a}}$ than to cover the lie by misreporting and receive $\underline{a}$, given that $\underline{a}+\epsilon -\frac{1}{\overline{a}}>\underline{a}$. Given the dominant strategy of type 2 and $\underline{a}>\underline{a}+\epsilon -\frac{1}{\underline{a}}$, it is a best-response for type 1 to report truthfully as well. Hence, all agents report truthfully in equilibrium and acquire zero education. In Fig. 1, contract $a_0$ denotes the offer to the workers, who report high productivity, when lies are detected.

3 The economy and definitions

The previous example was used to show that it is possible to eliminate asymmetric information problems if the realized frequency is common knowledge. We now proceed to show that this result is general and does not depend on the specifics of the example. First, we introduce the economy and some useful definitions.

3.1 Agents, types and type profiles

The economy consists of a finite set $\mathcal {N}$ of agents. N stands for the aggregate number of agents. $\varvec{\Uptheta }$ is the finite set of potential types with $\vartheta$ denoting a generic element in the set. $\varTheta$ denotes the aggregate number of types. In order to make our problem non-trivial we assume that $N \ge 2$ and $\varTheta \ge 2. \varvec{\omega } \in \varvec{\Uptheta }^N$ is a type profile, i.e., a vector which contains a draw of a type for each of the N agents in the economy. $\varvec{\omega }$ is drawn from $\varvec{\Uptheta }^N$ by a generic probability distribution $f(\varvec{\omega })$, that is $f:\varvec{\Uptheta }^N \rightarrow \varDelta ^{\varvec{\Uptheta }^N}$, where $\varDelta ^{\varvec{\Uptheta }^N}$ is the unit simplex over $\varvec{\Uptheta }^N$, i.e., $\{f \in \varvec{R}_+|\sum _{\varvec{\omega }\in \varvec{\Uptheta }^N} f(\varvec{\omega })=1\}$.

3.2 Information structure and realized frequency of types

It is assumed that each agent has private information about his own type, but does not know the types of the other agents, so that neither the agents nor the mechanism designer knows the realized type profile $\varvec{\omega }$. However, both the agents and the mechanism designer know the realized frequency of types $\varvec{\phi }$, where $\varvec{\phi }$ is a $\varTheta$-length vector with each element $\phi (\vartheta )$ denoting the proportion of agents who have type $\vartheta$ in the realized type profile $\varvec{\omega }$. That is, $\varvec{\phi }$ denotes the relative frequency of each type, which materializes after types are drawn. Thus, $N(\vartheta )=\phi (\vartheta )N$ is the total number of agents with type $\vartheta$. Since there are several type profiles which have the same realized frequency of types, let $\varOmega (\varvec{\phi })$ denote the set of all type profiles consistent with $\varvec{\phi }$.

3.3 Feasible allocations

Suppose that there are L goods in total in the economy which are distributed to and consumed by the agents, with $L \ge 2$. $\mathcal {L}$ denotes the set of goods. At least two of the goods in the economy are transferable and continuously divisible. If any of the goods is non-transferable, then it is a public good, i.e., all agents consume the same quantity of it.

An individual allocation $\varvec{a}_i$ is a L-length vector that specifies a quantity for each good to be distributed to individual i. An allocation $\varvec{a}$ is a $L\times N$-length vector that specifies an individual allocation for each agent.

Let $A(\mathcal {N},\varvec{\phi })$ be the set of all feasible allocations, with elements $\varvec{a} \in A(\varvec{\phi }) \subseteq \varvec{R}_+^{L \times N}$. Note that we allow the feasibility set to depend on $\varvec{\phi }$ but not on $\varvec{\omega }$. That is, we implicitly assume that whenever two type profiles imply the same frequency of realized types, they also imply the same feasibility constraints. In other words, only the types of the agents play a role in determining which allocations are feasible, not their identities. For any subset of agents $J, J \subseteq \mathcal {N}$, we also define $A(J,\varvec{\phi })$ to be the set of feasible allocations for the agents in J conditional on $\varvec{\phi }$, that is $A(J,\varvec{\phi }) \subseteq \varvec{R}_+^{L \times J}$.

Finally, note that later on in our analysis we focus on anonymous allocations that is on allocations where agents of the same type receive the same bundle of goods. Therefore, it is convenient to define individual allocations with respect to types rather than with respect to the agents’ identities. To separate the two, we denote by $\varvec{a}_{\vartheta }$ the type-specific individual allocation of an agent with type $\vartheta$, which is interpreted as the L-length vector of goods which the mechanism designer allocates to all agents of type $\vartheta$.

3.4 Utility functions and contour sets

$u:\varvec{R}^L\times \varvec{\Uptheta } \rightarrow \varvec{R}$ is the Bernoulli utility, which is assumed to be continuous and differentiable with respect to all the L arguments that represent goods. Hence, $u_{i}(\varvec{a}_i;\vartheta )$ denotes the utility of agent i from consuming individual allocation $\varvec{a}_i$, conditional on i’s type being $\vartheta$. In the analysis that follows, however, we simplify the notation to $u_{\vartheta }(\varvec{a}_{\vartheta })$ so that only an agent’s type and her type-specific individual allocation show up.

Furthermore, we assume that the utility functions for all types satisfy the single-crossing condition. Formally, for any pair of types  $\{\vartheta ,\eta \}\in \varvec{\Uptheta }$,  there exists at least one pair of goods  $\{k,l\}\in \mathcal {L}$,  such that $-\frac{\partial u_{\vartheta }/ \partial a_{\vartheta l} }{\partial u_{\vartheta }/ \partial a_{\vartheta k}}<-\frac{\partial u_{\eta }/ \partial a_{\eta l}}{\partial u_{\eta }/ \partial a_{\eta k}}$,  where $a_{\vartheta k}$ is the individual allocation of good k to type $\vartheta$. This condition is intuitive and is often used in the mechanism design literature.

The following definitions of lower and upper contour sets are also useful. $L_{\vartheta }(\varvec{a}_{\vartheta })$ is the lower contour set of an agent with type $\vartheta$ associated with a type-specific individual allocation $\varvec{a}_{\vartheta }$: $L_{\vartheta }(\varvec{a}_{\vartheta })=\{\varvec{c} \in \varvec{R}_+^L :u_{\vartheta }(\varvec{c}) < u_{\vartheta }(\varvec{a}_{\vartheta })\}$, and $V_{\vartheta }(\varvec{a}_{\vartheta })$ is the upper contour set of type $\vartheta$ associated with $\varvec{a}_{\vartheta }$: $V_{\vartheta }(\varvec{a}_{\vartheta })=\{\varvec{c} \in \varvec{R}_+^{L} :u_{\vartheta }(\varvec{c}) > u_{\vartheta }(\varvec{a}_{\vartheta })\}$.

3.5 Allocation rules, efficiency and anonymity

An allocation rule or social choice rule $\rho$ is a mapping from the set of type profiles consistent with $\varvec{\phi }$ to the set of feasible allocations, i.e., $\rho :\varOmega (\varvec{\phi }) \rightarrow A(\mathcal {N}, \varvec{\phi })$.

An allocation $\varvec{a}$ is (Pareto) efficient or first-best if there does not exist any other allocation $\varvec{b} \in A(\mathcal {N}, \varvec{\phi })$ such that $u_i(\varvec{b};\vartheta )>u_i(\varvec{a};\vartheta )$ for at least one agent $i \in \mathcal {N}$ and $u_j(\varvec{b};\eta ) \ge u_j(\varvec{a};\eta )$ for all other agents $j\in \mathcal {N}\!\setminus \! {i}$. Similarly, an allocation rule $\rho$ is (Pareto) efficient or first-best if for every type profile $\varvec{\omega }\in \varOmega (\varvec{\phi })$ it implements an efficient allocation $\varvec{a}(\varvec{\omega })$. In order to differentiate efficient allocations (allocation rules) from non-efficient ones we denote them by $\varvec{a}^* (\rho ^*)$. Thus, the definition of an efficient allocation rule can be formally expressed as $\rho ^*(\varvec{\omega })=\varvec{a}^*(\varvec{\omega }),~\forall \varvec{\omega }\in \varOmega (\varvec{\phi })$.

An allocation rule $\rho$ is anonymous if, for every $\varvec{\omega }\in \varOmega (\varvec{\phi })$, agents with the same type receive the same type-specific individual allocation. That is, every pair of agents $\{i,j\}\in \mathcal {N}$ that share the same type $\vartheta$ receives the same type-specific individual allocation $\varvec{a}_{\vartheta }$. Thus, for allocation rules that satisfy anonymity, an agent’s identity per-se has no impact on the agent’s final individual allocation. Anonymity is a desirable property for a social choice rule. In most cases of interest, economists are concerned with the economic characteristics of agents and not with their identity. Therefore, it is reasonable to assume that, if the distribution of these characteristics remains unchanged, so does the distribution of the economically desirable outcomes. It is also a property satisfied by many commonly used social choice rules, like the Walrasian correspondence and the utilitarian social welfare function.

Note that the definition of the allocation rule implies that anonymity is a property of the final allocation as well. This means that if an allocation is anonymous, then all agents with the same type receive the same individual allocation. A direct consequence of this is that any anonymous allocation $\varvec{a}$ can also be written as a $\varTheta$-length vector of type-specific individual allocations $\varvec{a}_{\vartheta }$. Thus, if an allocation $\varvec{a}^*$ is both efficient and anonymous, then it can be written as a $\varTheta$-length vector of first-best type-specific individual allocations, denoted by $\varvec{a}^*_{\vartheta }$. Since our main results concern efficient and anonymous allocation rules, the use of this notation is very convenient in simplifying their presentation.

More importantly, if the allocations in a set $\{\varvec{a}(\varvec{\omega })\}$ are anonymous and they share the same realized distribution of types $\varvec{\phi }$, then the set of type-specific individual allocations $\{\varvec{a}_{\vartheta }\}$ for the respective types in $\varvec{\Uptheta }$, as well the total number of bundles $\varvec{a}_{\vartheta }$ to be distributed to the agents of each type, are fixed by $\varvec{\phi }$ and they are independent of $\varvec{\omega }$. This has important implications for the implementation of an efficient and anonymous allocation rule $\rho ^*(\varvec{\omega })$. From the perspective of individual agents, each final allocation $\varvec{a}^*(\varvec{\omega })$ is distinct from all the other because agents may receive different bundles to consume depending on their type. But, viewed from the perspective of types, all $\varvec{a}^*(\varvec{\omega })$ contain the same type-specific individual allocations and in the same numbers, they are just reshuffled across different agents. In other words, a mechanism designer who is tasked with implementing an anonymous $\rho ^*(\varvec{\omega })$ with a fixed $\varvec{\phi }$ knows the number of agents of each type, and the bundle of goods each type should consume, but does not know who are the agents belonging to each type. Inducing agents to reveal this information truthfully is the main objective of implementation.

3.6 Mechanisms, incentive compatibility and self-selective sets

A direct mechanism $M_s(J_s, \varvec{m}_s, h_s, g_s)$ is a game form with a sequence $s=\{1,2,\ldots ,S\}$ of stages, $S<+\infty . \mathcal {S}$ denotes the set of all stages. $J_s$ is the set of agents participating at stage $s. \varvec{m}_s$ is a message profile , i.e., a report $m_{is}$ of her type by every agent i in $J_s$. The set of all possible message profiles at stage s is $\mathcal {M}_s$, while $\varvec{m}_{-i,s}$ denotes a type profile for all other agents apart from agent $i. h_s: \mathcal {M}_s\rightarrow J_{s+1}, \,J_{s+1}\subseteq J_s$, is a mapping from the set of message profiles to the set of agents who continue to stage $s+1.\, g_s: \mathcal {M}_s\rightarrow A(J_{s}\setminus J_{s+1},\varvec{\phi })$ is a mapping from the set of message profiles to the set of allocations to the agents who exit the mechanism at stage s. If $J_{s+1}=J_s$, then $g_s=\emptyset$.

A sequence of message profiles $\{\varvec{m}^*_s|s\in \mathcal {S}\}$ constitutes a perfect Bayesian equilibrium of the mechanism $M_s$ if $\sum _{\varvec{m}^*_{-i,s}} v_{is}(m^*_{is},\varvec{m}^*_{-i,s}) d_s(\varvec{m}^*_{-i,s}) \ge \sum _{\varvec{m}^*_{-i,s}} v_{is}(m_{is},\varvec{m}^*_{-i,s}) d_s(\varvec{m}^*_{-i,s}) , \forall m_{is} \in \mathcal {M}_{is}, \forall i\in J_s, and \forall ~s\in \mathcal {S}$, where $v_{is}(\varvec{m}_s)$ is the indirect utility of agent i at stage s under the message profile $\varvec{m}_s$, $d_s(\varvec{m}_{-i,s})$ is the probability that all other agents than i play the message profile $\varvec{m}_{-i,s}$, and $\mathcal {M}_{is}\subseteq \varvec{\Uptheta }$ is agent’s i message set at stage s.³ Similarly, a mechanism $M_s$ is incentive compatible if, for every agent i with type $\vartheta$, $\sum _{\varvec{\theta }_{-i}} v_{is}(\vartheta ,\varvec{\theta }_{-i}) d_s(\varvec{\theta }_{-i}) \ge \sum _{\varvec{\theta }_{-i}} v_{is}(m_{is},\varvec{\theta }_{-i}) d_s(\varvec{\theta }_{-i}) , \forall ~ m_{is} \in \mathcal {M}_{is}, \,\forall i\in J_s, and\, \forall s\in \mathcal {S}$, where $\varvec{\theta }_{-i}$ is the type profile of all agents apart from i. That is, a mechanism is incentive compatible when it is in the self-interest of every agent to report her type truthfully, conditional on the other agents reporting their type truthfully. Apart from the above common definitions, we also provide the following definitions of self-selective type-specific individual allocation and self-selective set of individual allocations, which are useful in proving our main result.

Given a set of types $J\subseteq \varvec{\Uptheta }$, the set $\hat{A}$ of type-specific individual allocations is a self-selective set of type-specific individual allocations or simply a self-selective set, if the set contains as many type-specific individual allocations as the number of types in the set J, and if, for each type $\vartheta \in J$, there exists a type-specific individual allocation $\varvec{\hat{a}}_{\vartheta } \in \hat{A}$ such that $u_{\vartheta }(\varvec{\hat{a}}_{\vartheta }) > u_{\vartheta }(\varvec{a}_{\eta }),~~\forall ~ \eta \in J\setminus \vartheta$. Any individual allocation that belongs to a self-selective set $\hat{A}$ is called a self-selective type-specific individual allocation. Simply put, the notion of self-selectiveness asserts that if a subset of types were left to choose a single type-specific individual allocation from a self-selective set, then each type would strictly prefer one of them over all other. This way agents truthfully reveal their type through their choice. This is useful for us because we use appropriately designed self-selective sets as out-of-equilibrium-path allocations in order to ensure the incentive compatibility of our mechanism.

3.7 Remarks

Overall, the economy is described by the following primitives: $E=\{\mathcal {N}, \varvec{\Uptheta }, A(\mathcal {N},\varvec{\phi }), \varvec{\phi }, u\}$. This modeling of the economy is very flexible and can be easily extended to various dimensions. For example, the model allows for public goods problems, since some elements of the individual allocations can be common. Also, since we impose no restrictions on $\varvec{\phi }$ or the type-generating process that produces $\varvec{\phi }$, types may or may not be independently distributed. Thus, several commonly used type-generating processes, such as Markov chains, are compatible with our formulation.

Furthermore, the model can be easily extended to include inter-dependent valuations for agents. For example, one may write the utility of agents as a function of both their own type and the type of other agents, $u_{i}(\varvec{a}_i;\vartheta ,\varvec{\theta }_{-i})$. Or one may write the utility as a function of the realized distribution of types, $u_{i}(\varvec{a}_i;\vartheta ,\varvec{\phi })$, if agents’ identities do not play a role in other agents’ utilities. In either case, as long as the effect of $\varvec{\theta }_{-i}$ and $\varvec{\phi }$ on u is identical across agents of the same type, so that the notation $u_{\vartheta }(.)$ correctly represents our model, all of the arguments and the results of the following section follow.

Finally, our model can be extended to economies with uncertainty. For example, let $\varvec{\pi }:\varvec{\phi }\rightarrow \varDelta ^{Z}$ be the probability distribution function over states, where Z the finite set of states and $\varDelta ^Z$ is the unit simplex $\{\varvec{\pi }\in \varvec{R}^Z_+|\sum _{z\in Z}\pi _z=1\}$. In this case, $Y=Z\times L$, where L is the finite set of final goods and Y is the set of state-dependent goods. Thus, for a $\vartheta$-type agent, her expected utility function is given by  $u_{\vartheta }(\varvec{a}_{\vartheta };\varvec{\phi })=\sum _{z\in Z}x_{\vartheta }(\varvec{a}_{\vartheta },z)\pi _z(\varvec{\phi })$,  where  $x_{\vartheta }(\varvec{a}_{\vartheta },z)$  is the decision-outcome payoff in state z. This formulation allows one to introduce uncertainty into the primitives of the economy while keeping the main framework unaffected, and thus our results apply equally well to it.

4 Implementation of first-best allocations

The main result of the paper is that any anonymous efficient social choice rule $\rho ^*(\varvec{\omega })$ can be uniquely implemented in perfect Bayesian equilibrium in a finite sequential mechanism, i.e., for each $\varvec{\omega }\in \varOmega ( \varvec{\phi })$, the unique perfect Bayesian equilibrium outcome of the mechanism is $\rho ^*(\varvec{\omega })= \varvec{a}^*(\varvec{\omega })$.

In order to prove this result we proceed as follows. First, we show that Pareto efficiency implies a ranking of types according to envy (Lemma 1). This property is exploited in the design of the out-of-equilibrium-path allocations. Specifically, we show that the combination of the single-crossing condition with the result of Lemma 1 allows one to construct self-selective sets of type-specific individual allocations (Lemma 2). Each set contains type-specific individual allocations which are situated in the neighborhood of one of the first-best type-specific individual allocations $\varvec{a}^*_{\vartheta }$ constituting $\varvec{a}^*(\varvec{\omega })$. The self-selective sets designed according to Lemma 2 are used as out-of-equilibrium-path allocations for each one of the stages of the mechanism. Finally, we combine these two results to prove our main theorem on the implementation of the efficient social choice rule. All proofs are provided in “Appendix.”

We start the analysis with the result that any Pareto efficient and anonymous allocation $\varvec{a}^*$ implies a ranking of types according to envy.

Lemma 1

If $\varvec{a}^*$ is a Pareto efficient and anonymous allocation, then, for any $\varvec{\check{\Uptheta }} \subseteq \varvec{\Uptheta }$ and the corresponding set of type-specific individual allocations $\check{A}=\{\varvec{a}^*_{\vartheta }: \vartheta \in \varvec{\check{\Uptheta }}\}$, there exists at least one type $\vartheta \in \varvec{\check{\Uptheta }}$, who does not envy any of the other type-specific individual allocations in $\check{A}$: $u_{\vartheta }(\varvec{a}^*_{\vartheta }) \ge u_{\vartheta }(\varvec{a}_{\eta }^*), ~\forall ~ \varvec{a}^*_{\eta } \in \check{A}$.

Lemma 1 allows one to construct a complete ranking of types according to envy. In particular, let $\mathcal {K}=\{\vartheta \in \varvec{\Uptheta }: u_{\vartheta }(\varvec{a}^*_{\vartheta }) \ge u_{\eta }(\varvec{a}_{\eta }^*), ~\forall \eta \in \varvec{\Uptheta } \}$ be the set of types who do not envy the type-specific individual allocation of any other type. By Lemma 1, we know that this set is non-empty. Then, by removing set $\mathcal {K}$ from the set of types $\varvec{\Uptheta }$ and applying Lemma 1 again to the remaining set, one obtains the set $\mathcal {K}-1=\{\vartheta \in \varvec{\Uptheta }: u_{\vartheta }(\varvec{a}^*_{\vartheta }) \ge u_{\eta }(\varvec{a}_{\eta }^*), ~\forall \eta \in \varvec{\Uptheta }-\mathcal {K}\}$. By iteration, one may define a total number of K envy sets, $\{\mathcal {K}, \mathcal {K}-1, \mathcal {K}-2,\ldots ,1\}$, $1 \le K \le \varTheta$, ranked according to envy from the “highest” envy set $\mathcal {K}$ to the “lowest” set 1, such that the types in each one of them (say envy set $\mathcal {K}-k$) do not envy any of the types in their own set or lower sets (any $\mathcal {K}-l$, with $l\ge k$), but they envy some type(s) in a higher set (some type in an envy set $\mathcal {K}-l, ~l<k$).⁴

The K envy sets defined above could be used to construct a mechanism which induces all types to reveal their type truthfully. However, such a mechanism would involve tedious case distinctions across envy sets. In order to simplify the required mechanism we rank types within each envy set that contains multiple types so that the mechanism is implemented over a full ranking of types. This can be achieved because the way these envy sets are constructed ensures that there is no envy between types which belong to the same envy set. For the rest of the analysis we assume that the mechanism designer ranks types according to the following simple rules:

• 1. Types who belong to a higher envy set are ranked above types who belong to a lower envy set.

• 2. If two types, $\vartheta$ and $\eta$, belong to the same envy set and $u_{\vartheta }(\varvec{a}^*_{\vartheta })> u_{\vartheta }(\varvec{a}^*_{\eta })$, $u_{\eta }(\varvec{a}^*_{\eta })= u_{\eta }(\varvec{a}^*_{\vartheta })$, then type $\vartheta$ receives higher ranking than type $\eta$.

• 3. If two types, $\vartheta$ and $\eta$, belong to the same envy set and $u_{\vartheta }(\varvec{a}^*_{\vartheta })> u_{\vartheta }(\varvec{a}^*_{\eta })$, $u_{\eta }(\varvec{a}^*_{\eta })> u_{\eta }(\varvec{a}^*_{\vartheta })$, then the ranking between the two types is arbitrarily determined as long as it is compatible with rules 1 and 2 above whenever comparing the rank of types $\vartheta$ and $\eta$ with the rest of the types.

Two notes are worth making at this point. First, in order for the ranking of types to be complete, one should also examine the case where $\vartheta$ and $\eta$ belong to the same envy set and $u_{\vartheta }(\varvec{a}^*_{\vartheta })= u_{\vartheta }(\varvec{a}^*_{\eta })$, $u_{\eta }(\varvec{a}^*_{\eta })= u_{\eta }( \varvec{a}^*_{\vartheta })$. However, this case is incompatible with single-crossing and so it is impossible to occur. Second, the ranking of types implied by rule 2 satisfies transitivity; hence, it is consistent.⁵

Overall, by following the above rules, the mechanism designer ranks all types according to envy from the type with the lowest rank, type 1, to the type with the highest rank, type $\varTheta$. From this point forward we use $\vartheta$ to denote the rank of a type, so that $1 \le \vartheta \le \varTheta$. By the construction of this ranking, type $\varTheta$ does not envy the first-best type-specific individual allocation of any other type. A generic type $\vartheta$ may envy the first-best type-specific individual allocation of a higher type ($\kappa >\vartheta$), but does not envy the first-best type-specific individual allocation of any type with lower rank ($\eta <\vartheta$).⁶

The next step is to exploit the ranking of types and the single-crossing property to construct self-selective sets of type-specific individual allocations in the neighborhood of every first-best type-specific individual allocation contained in any $\varvec{a}^*(\varvec{\omega })$. These self-selective sets are used as out-of-equilibrium-path allocations in the mechanism, and they serve the purpose of “punishments” for misreporting types. To be more precise, given a complete ranking of types created by applying the rules above, for each type $\vartheta$ with respective first-best type-specific individual allocation $\varvec{a}^*_{\vartheta }$, we construct a self-selective set of type-specific individual allocations $\hat{A}(\varvec{a}^*_{\vartheta })$ such that (i) it contains $\varvec{a}^*_{\vartheta }$, and (ii) it contains a self-selective type-specific individual allocation for every type which has higher rank than type $\vartheta$ in an $\epsilon$-neighborhood of $\varvec{a}^*_{\vartheta }$, where $\epsilon$ is an arbitrarily small positive number. This means that any type with rank higher than $\vartheta$ prefers one of the type-specific individual allocations in $\hat{A}(\varvec{a}^*_{\vartheta })$ over all others. Lemma 2 below proves that the single-crossing condition allows one to construct self-selective sets with the above properties in the neighborhood of any $\varvec{a}^*_{\vartheta }$.

Lemma 2

Suppose that the single-crossing condition on utility functions holds and consider a first-best allocation $\varvec{a}^*(\varvec{\omega })$ with type-specific individual allocations $\varvec{a}^*_{\vartheta },~\forall ~\vartheta \in \varvec{\Uptheta }$ and a complete ranking of types according to envy from the type with the lowest rank, type 1, to the type with the highest rank, type $\varTheta$. Then, for every $\varvec{a}^*_{\vartheta }\in \varvec{a}^*(\varvec{\omega })$,  $1\le \vartheta \le \varTheta -1$,  there exists $\epsilon >0$ small enough and a set of self-selective type-specific individual allocations $\hat{A}(\varvec{a}^*_{\vartheta })$ such that:

• (i) $\varvec{a}^*_{\vartheta }\in \hat{A}(\varvec{a}^*_{\vartheta })$

• (ii) there exists $\varvec{\hat{a}}_{\eta }\in \hat{A}(\varvec{a}^*_{\vartheta })$ such that: $u_{\eta }(\varvec{\hat{a}}_{\eta })> u_{\eta }(\varvec{\hat{a}}_{\zeta }),~\forall ~\varvec{\hat{a}}_{\zeta }\in \hat{A}(\varvec{a}^*_{\vartheta }),$ $~\varvec{\hat{a}}_{\zeta }\ne \varvec{\hat{a}}_{\eta }, ~\forall ~\eta :~\vartheta \le \eta \le \varTheta$

• (iii) $\Vert \varvec{a}^*_{\vartheta }-\varvec{\hat{a}}_{\eta } \Vert \le \epsilon ,~\forall ~\varvec{\hat{a}}_{\eta }\in \hat{A}(\varvec{a}^*_{\vartheta })$

• (iv) $u_{\eta }(\varvec{a}^*_{\eta })>u_{\eta }(\varvec{\hat{a}}_{\eta }),~\forall ~\eta :~\vartheta <\eta \le \varTheta$

Recall from Sect. 3 that the set of first-best type-specific individual allocations, $\varvec{a}^*_{\vartheta }$, contained in $\varvec{a}^*(\varvec{\omega })$ is the same across all $\varvec{\omega }\in \varOmega (\varvec{\phi })$. Therefore, any self-selective set with the properties of Lemma 2 is independent of $\varvec{\omega }$, i.e., it retains its properties across all $\varvec{\omega }\in \varOmega (\varvec{\phi })$.

The results in Lemmas 1 and 2 are useful in designing a sequential mechanism which implements the first-best allocation rule as a unique perfect Bayesian equilibrium. The proof of this result is provided in “Appendix.” Here, we provide a verbal presentation of the mechanism and a sketch of the arguments used in the proof.

The mechanism consists of $\varTheta -1$ stages, one less than the total number of types, which is $\varTheta$. Each stage is designed so as to incentivize the agents of a particular type (the “target” type) to report truthfully their type, receive the respective first-best type-specific individual allocation for this type, and exit the mechanism. The first stage of the mechanism is designed for type 1, and each successive stage is designed for the type with rank one level higher than the type of the previous stage. The final stage, stage $\varTheta -1$, is designed for the two types with the highest rank, types $\varTheta -1$ and $\varTheta$.

In particular, at each stage, all agents who participate in it are asked to report their type. If the number of reports for the “target” type equals the realized number of agents with this type (which is known through $\varvec{\phi }$), then the agents who report this type receive the respective first-best type-specific individual allocation of this type and exit the mechanism, while the agents, who report any other type, move to the next stage. If, on the other hand, the number of reports for the “target” type does not equal the realized number of agents with this type, then the mechanism terminates at this stage and all agents receive the self-selective type-specific individual allocation of the type they reported in that stage (i.e., their last report) from a set which has the properties of Lemma 2. Finally, if the mechanism does not terminate in any of the previous stages, the last stage of the mechanism is stage $\varTheta -1$.

The main reason that the above mechanism works is because, at each stage, types of higher rank than the “target” type strictly prefer to report truthfully their type than to report the “target” type, irrespective of the reports of the rest of the agents. In particular, if they expect the mechanism to end at the current stage, they prefer to report truthfully, and thus pick their most preferred type-specific individual allocation from the corresponding self-selective set triggered by the mechanism’s termination, than to report any other type. And if they expect that the mechanism will not terminate at the current stage, then they prefer not to report the “target” type, because the continuation payoff from the mechanism is higher than exiting with the type-specific individual allocation of the “target” type. The last point holds because types of higher rank do not envy the “target” type’s first-best type-specific individual allocation. Since higher rank types do not report this type, the best-response of agents of the “target” type is to report truthfully and by induction the result obtains.

Before the presentation of the theorem, a couple of remarks are noteworthy. First, the sequential nature of the mechanism used in the proof is not a necessary element of the result, i.e., one can find equivalent static mechanisms that implement the efficient allocation rule as a unique Bayesian equilibrium. Even though static mechanisms are less notation-heavy, they involve more case distinctions than our sequential mechanism, which makes the proof longer and more tedious. For the sake of elegance and transparency we opt for the sequential mechanism presented in detail in “Appendix.”

Second, we remark again that, because $\varvec{a}^*(\varvec{\omega })$ is anonymous and $\varvec{\phi }$ is common knowledge, the first-best type-specific individual allocations $\{\varvec{a}^*_{\vartheta }\}$ and the total number of bundles for each type are the same for every $\varvec{a}^*(\varvec{\omega })$. It is only the identity of the agents who belong in each type that it is not known across each $\varvec{\omega } \in \varOmega (\varvec{\phi })$. Therefore, a mechanism implements $\rho ^*(\varvec{\omega })$ if it induces agents to report their type truthfully and if it allocates to them the respective first-best type-specific individual allocation of the type they report.

Theorem 1

If the realized distribution of types is common knowledge and preferences satisfy the single-crossing condition, then there exists a mechanism which implements any Pareto efficient and anonymous allocation rule $\rho ^*(\varvec{\omega })$ as the unique perfect Bayesian equilibrium. In this equilibrium each agent reports her private information truthfully and receives the first-best type-specific individual allocation corresponding to her type.

Before concluding, we would like to briefly comment on the advantages our mechanism presents in comparison with the existing literature on implementation (see, e.g., Jackson (1991), Maskin (1999). First, our mechanism holds even with two agents (or even in the degenerate case of one agent). Second, the required message space is minimal, since agents send messages only about their own type. Third, we do not require any ad hoc game, which has no equilibrium in pure strategies (like an integer game), in order to rule out undesirable equilibria. This is achieved by “enticing” some of the misreporting agents to report truthfully, whenever there are multiple misrepresentations. Finally, even though the domain of preferences we consider is strictly smaller than in many other papers, still our assumptions on utility functions are relatively weak and there are many cases of interest that comply with them.

5 Conclusion

In this paper, we consider a general hidden-type economy and, under relatively weak conditions, we show that it is possible to construct a mechanism which has a unique perfect Bayesian equilibrium, where all agents reveal their type truthfully and they receive a first-best individual allocation. If the realized frequencies of types are known, then one can aggregate the messages that all agents send and uncover any misreport(s), even if the identity of the liar is not known.

Truth-telling, however, requires appropriately designed punishments for lying. If the punishment from detecting a lie is too severe, then some agents may deliberately lie about their type in order to force other agents to also do so. The lies cancel out and the former agents “steal” the individual allocations of the latter, who are forced to lie under the fear of extreme punishments. This can lead to coordination failures and multiplicity of equilibria. Therefore, uniqueness of the equilibrium requires a careful construction of the individual allocations when lies are detected. We show that such punishments exist when the single-crossing condition holds.

Appendix

1.1 Proof of Lemma 1

First note that, by the assumptions made on the nature of the goods in this economy (i.e., either transferable private goods or public goods), it is possible to reallocate individual allocations from one agent to another. For example, it is possible for the mechanism designer to take a type-specific individual allocation $\varvec{a}_{\vartheta }$ from agent i of type $\vartheta$ and give it to agent j of type $\eta$, while j’s type-specific allocation $\varvec{a}_{\eta }$ may be reallocated to agent h and so on.

Then, consider a Pareto efficient and anonymous allocation $\varvec{a}^*$ with type-specific individual allocations $\varvec{a}^*_{\vartheta }$ and suppose that Lemma 1 does not hold for some subset $\check{\varTheta }$ of types, $\varvec{\check{\Uptheta }} \subseteq \varvec{\Uptheta }$, with corresponding set of type-specific individual allocations $\check{A}=\{\varvec{a}^*_{\vartheta }|~\forall ~ \vartheta \in \varvec{\check{\Uptheta }}\}$. This means that all types in $\varvec{\check{\Uptheta }}$ envy the type-specific individual allocation of at least one other type: $\forall ~\varvec{a}^*_{\vartheta }\in \check{A}, ~\exists ~ \eta \in \varvec{\check{\Uptheta }}, \eta \ne \vartheta : u_{\vartheta }(\varvec{a}^*_{\eta }) > u_{\vartheta }(\varvec{a}^*_{\vartheta })$. But, since this holds for all types, then there exists at least one reassignment of the type-specific individual allocations among the agents with types in $\varvec{\check{\Uptheta }}$ such that some of them are made strictly better-off and the rest remain as well-off as under the original allocation $\varvec{a}^*$.

For example, one could create a reassignment cycle by taking one agent from an arbitrary type, reassign to her one of the type-specific individual allocations that she envies, then proceed to the agent from whom the type-specific individual allocation was taken from, reassign to her one of the type-specific individual allocations that she envies, and so on, until the cycle returns back to one of the agents whose type-specific individual allocation has been reassigned. Because the set of agents is finite such a cycle is guaranteed to exist. Agents not involved in the cycle retain the type-specific individual allocations under $\varvec{a}^*$.

However, the existence of such a cycle constitutes a Pareto improvement for a subset of agents in $\mathcal {N}$ and violates the initial assumption that $\varvec{a}^*$ is Pareto efficient. $\square$

1.2 Proof of Lemma 2

The proof is done by the construction of a self-selective set that satisfies the properties of Lemma 2 with respect to an arbitrary type $\vartheta$. For this purpose recall the definitions of upper contour set and lower contour set from Sect. 3, and consider a first-best and anonymous allocation $\varvec{a}^*(\varvec{\omega })$ and the corresponding first-best type-specific individual allocations $\varvec{a}^*_{\vartheta }$, for any $\vartheta \in \varvec{\Uptheta }$. We use the single-crossing condition of utility functions and the complete ranking of types according to envy, which is possible as a result of Lemma 1 and which is assumed to satisfy the ranking rules 1–3 of page 10, to construct the required self-selective set. To show that this is possible, we take a type of an arbitrary rank $\vartheta$, $1\le \vartheta \le \varTheta$ and consider the following algorithm for picking a sequence of type-specific individual allocations $\varvec{\hat{a}}_{\eta }$ to be the elements of the self-selective set $\hat{A}(\varvec{a}^*_{\vartheta })$.

First, take $\varvec{a}^*_{\vartheta }$ itself to be the first element of the set. Then use $\varvec{a}^*_{\vartheta }$ as a starting point and pass the indifference curves of types $\vartheta$ and $\vartheta +1$ from this point. By the single-crossing condition, the set $V_{\vartheta +1}(\varvec{a}^*_{\vartheta }) \cap L_{\vartheta }(\varvec{a}^*_{\vartheta })$ is non-empty. For some $\epsilon >0$ to be defined precisely later in the analysis, pick a type-specific individual allocation $\varvec{\hat{a}}_{\vartheta +1}$ in the set $V_{\vartheta +1}(\varvec{a}^*_{\vartheta }) \cap L_{\vartheta }(\varvec{a}^*_{\vartheta })$, such that $\Vert \varvec{a}^*_{\vartheta }-\varvec{\hat{a}}_{\vartheta +1} \Vert \le \frac{\epsilon }{\varTheta -\vartheta }$, to be the second element in $\hat{A}(\varvec{a}^*_{\vartheta })$. In the last expression, $\varTheta -\vartheta$ is the natural number that represents the difference between the ranks of the type with the highest rank, $\varTheta$, with the rank of type $\vartheta$. Also, because the utility functions are assumed to be continuous with respect to goods, it is always possible to find $\varvec{\hat{a}}_{\vartheta +1}$ in the set $V_{\vartheta +1}(\varvec{a}^*_{\vartheta }) \cap L_{\vartheta }(\varvec{a}^*_{\vartheta })$ such that $\Vert \varvec{a}^*_{\vartheta }-\varvec{\hat{a}}_{\vartheta +1} \Vert \le \frac{\epsilon }{\varTheta -\vartheta }$ for any $\epsilon >0$. Finally, note that, by construction, type $\vartheta$ strictly prefers $\varvec{a}^*_{\vartheta }$ to $\varvec{\hat{a}}_{\vartheta +1}$, while type $\vartheta +1$ strictly prefers $\varvec{\hat{a}}_{\vartheta +1}$ to $\varvec{a}^*_{\vartheta }$.

With $\varvec{\hat{a}}_{\vartheta +1}$ as a new starting point, reiterate the above procedure for types $\vartheta +1$ and $\vartheta +2$ to pick $\varvec{\hat{a}}_{\vartheta +2}$ in the intersection of the lower contour sets of types $\vartheta$ and $\vartheta +1$ with the upper contour sets of types $\vartheta +1$ and $\vartheta +2$, $\left[ V_{\vartheta +1}(\varvec{a}^*_{\vartheta }) \cap L_{\vartheta }(\varvec{a}^*_{\vartheta })\right] \cap \left[ V_{\vartheta +2}(\varvec{\hat{a}}_{\vartheta +1}) \cap L_{\vartheta +1}(\varvec{\hat{a}}_{\vartheta +1})\right]$,  such that $\Vert \varvec{\hat{a}}_{\vartheta +1}- \varvec{\hat{a}}_{\vartheta +2} \Vert \le \frac{\epsilon }{\varTheta -\vartheta }$ . Again, because of the continuity of the utility functions, the intersection $V_{\vartheta +1}(\varvec{a}^*_{\vartheta })\cap L_{\vartheta }(\varvec{a}^*_{\vartheta }) \cap V_{\vartheta +2}(\varvec{\hat{a}}_{\vartheta +1}) \cap L_{\vartheta +1}(\varvec{\hat{a}}_{\vartheta +1})$ is non-empty and a type-specific individual allocation $\varvec{\hat{a}}_{\vartheta +2}$ satisfying the above conditions exists. Note that, because $\varvec{\hat{a}}_{\vartheta +2} \in L_{\vartheta +1}( \varvec{\hat{a}}_{\vartheta +1})$ and $\varvec{\hat{a}}_{\vartheta +1} \in L_{\vartheta }(\varvec{a}^*_{\vartheta })$, then $\varvec{\hat{a}}_{\vartheta +2} \in L_{\vartheta }(\varvec{a}^*_{\vartheta })$, so $\vartheta$ strictly prefers $\varvec{a}^*_{\vartheta }$ to $\varvec{\hat{a}}_{\vartheta +2}$. Similarly, $\varvec{\hat{a}}_{\vartheta +2} \in V_{\vartheta +2}(\varvec{\hat{a}}_{\vartheta })$, so $\vartheta +2$ strictly prefers $\varvec{\hat{a}}_{\vartheta +2}$ to $\varvec{a}^*_{\vartheta }$. Finally, $\vartheta +1$ strictly prefers $\varvec{\hat{a}}_{\vartheta +1}$ to $\varvec{a}^*_{\vartheta }$ by the previous step in selecting $\varvec{\hat{a}}_{\vartheta +1}$, and strictly prefers $\varvec{\hat{a}}_{\vartheta +1}$ to $\varvec{\hat{a}}_{\vartheta +2}$ by the current step in selecting $\varvec{\hat{a}}_{\vartheta +2}$. Thus the sequence of type-specific individual allocations $\{\varvec{a}^*_{\vartheta },\varvec{\hat{a}}_{\vartheta +1},\varvec{\hat{a}}_{\vartheta +2}\}$ constitutes a self-selective set for types $\vartheta , \vartheta +1$ and $\vartheta +2$.

With $\varvec{\hat{a}}_{\vartheta +2}$ as a new starting point and by iterating the above procedure $\varTheta -\vartheta -2$ additional times, one picks a sequence of type-specific individual allocations $\{\varvec{a}^*_{\vartheta },\varvec{\hat{a}}_{\vartheta +1},\ldots ,\varvec{\hat{a}}_{\varTheta }\}$ which satisfies properties (i), (ii) and (iii) of Lemma 2. In particular, note that for any type $\eta$ with rank $\vartheta < \eta \le \varTheta$, we have that $\Vert \varvec{a}^*_{\vartheta } - \varvec{\hat{a}}_{\eta }\Vert \le \Vert \varvec{a}^*_{\vartheta }-\varvec{\hat{a}}_{\vartheta +1}\Vert + \sum \nolimits _{k=1}^{\eta -\vartheta -1} \Vert \varvec{\hat{a}}_{\vartheta +k} - \varvec{\hat{a}}_{\vartheta +k+1} \Vert$ $\le (\eta -\vartheta ) \frac{\epsilon }{\varTheta -\vartheta } \le \epsilon$, so property (iii) is verified (clearly, this property holds for $\varvec{a}^*_{\vartheta }$ too).

It remains to define an appropriate $\epsilon$ such that property (iv) also holds. Define $\delta (\vartheta ,\eta )=\min \{ \Vert \varvec{a}^*_{\vartheta }-\varvec{a}_{\eta }\Vert ~|~\forall ~ \varvec{a}_{\eta } \in I_{\eta }(\varvec{a}^*_{\eta })\}$ to be the minimum distance between $\varvec{a}^*_{\vartheta }$ and the indifference curve $I_{\eta }(\varvec{a}^*_{\eta })$ of type $\eta$ which passes through her first-best type-specific individual allocation. Define $\delta _{\vartheta }^{min}= \min \{\delta (\vartheta ,\eta )~~ | ~~\forall ~\eta ~,~\vartheta <\eta \le \varTheta \}$ to be the minimum distance between $\varvec{a}^*_{\vartheta }$ and the indifference curves of all types with rank higher than $\vartheta$ which pass through their respective first-best type-specific individual allocations. Then for any $\epsilon <\delta _{\vartheta }^{min}$ property (iv) of Lemma 2 holds, because all the type-specific individual allocations in $\hat{A}(\varvec{a}^*_{\vartheta })$ are at most distance $\epsilon$ away from $\varvec{a}^*_{\vartheta }$. Therefore, they belong to $\bigcap \nolimits _{k=1}^{\varTheta -\vartheta } L_{\vartheta +k}(\varvec{a}^*_{\vartheta +k})$, where $L_{\vartheta +k}(\varvec{a}^*_{\vartheta +k})$ is the lower contour of type $\vartheta +k,~k\ge 1,$ that is associated with the first-best type-specific individual allocation $\varvec{a}^*_{\vartheta +k}$.

Overall, the sequence of type-specific individual allocations $\{\varvec{a}^*_{\vartheta },\varvec{\hat{a}}_{\vartheta +1},\ldots ,\varvec{\hat{a}}_{\varTheta }\}$ that constitutes $\hat{A}(\varvec{a}^*_{\vartheta })$ is assumed to be constructed for some $\epsilon <\delta _{\vartheta }^{min}$ and hence properties (i)-(iv) of Lemma 2 hold. $\square$

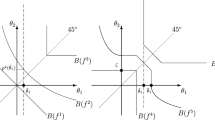
The figure in the next page depicts the construction of a self-selective set that satisfies the properties of Lemma 2 for the case where there are two goods and three types, types 1, 2 and 3, with corresponding ranking, in the economy (Fig. 2).

Fig. 2

A self-selective set for two goods and three types

1.3 Proof of transitivity of rule 2 on the complete ranking of types

Lemma 3

Suppose that types $\vartheta , \eta$, and $\zeta$, with corresponding type-specific individual allocations $\varvec{a}^*_{\vartheta }, \varvec{a}^*_{\eta }$, and $\varvec{a}^*_{\zeta }$, belong to the same envy set and suppose that: (i) $u_{\vartheta }(\varvec{a}^*_{\vartheta })> u_{\vartheta }(\varvec{a}^*_{\eta }), u_{\eta }(\varvec{a}^*_{\vartheta })= u_{\eta }(\varvec{a}^*_{\eta }),~(ii) u_{\eta }(\varvec{a}^*_{\eta })> u_{\eta }(\varvec{a}^*_{\zeta }), u_{\zeta }(\varvec{a}^*_{\eta })= u_{\zeta }(\varvec{a}^*_{\zeta })$. Then $u_{\vartheta }(\varvec{a}^*_{\vartheta })>u_{\vartheta }(\varvec{a}^*_{\zeta })$.

Proof

We prove the result by case elimination. There are two other cases possible, $u_{\vartheta }(\varvec{a}^*_{\vartheta })<u_{\vartheta }(\varvec{a}^*_{\zeta })$ and $u_{\vartheta }(\varvec{a}^*_{\vartheta })=u_{\vartheta }(\varvec{a}^*_{\zeta })$. We show that either of them is in contradiction with the assumption of single-crossing of the utility functions and the assumptions in the statement of Lemma 3.

(a) $u_{\vartheta }(\varvec{a}^*_{\vartheta })<u_{\vartheta }(\varvec{a}^*_{\zeta })$:  This case is impossible to occur because it violates the assumption that all three types belong to the same envy set and therefore $\vartheta$ does not envy $\zeta$.

(b) $u_{\vartheta }(\varvec{a}^*_{\vartheta })=u_{\vartheta }(\varvec{a}^*_{\zeta })$:  This case contains two subcases, (i) $u_{\zeta }(\varvec{a}^*_{\vartheta })=u_{\zeta }(\varvec{a}^*_{\zeta })$ and (ii) $u_{\zeta }(\varvec{a}^*_{\vartheta })<u_{\zeta }(\varvec{a}^*_{\zeta })$. The subcase $u_{\zeta }(\varvec{a}^*_{\vartheta })>u_{\zeta }(\varvec{a}^*_{\zeta })$ is not examined for the same reason as the case $u_{\vartheta }(\varvec{a}^*_{\vartheta })<u_{\vartheta }(\varvec{a}^*_{\zeta })$.

(i) Suppose $u_{\zeta }(\varvec{a}^*_{\vartheta })=u_{\zeta }(\varvec{a}^*_{\zeta })$. But in this case, we have that both types $\vartheta$ and $\zeta$ are indifferent between their two first-best type-specific individual allocations $\varvec{a}^*_{\vartheta }$ and $\varvec{a}^*_{\zeta }$, which violates the single-crossing assumption. Hence this case is impossible to hold.

(ii) Suppose $u_{\zeta }(\varvec{a}^*_{\vartheta })<u_{\zeta }(\varvec{a}^*_{\zeta })$. By $u_{\eta }(\varvec{a}^*_{\vartheta })= u_{\eta }(\varvec{a}^*_{\eta })$ and $u_{\vartheta }(\varvec{a}^*_{\vartheta })> u_{\vartheta }(\varvec{a}^*_{\eta })$, we have that $\varvec{a}^*_{\eta }\in I_{\eta }(\varvec{a}^*_{\vartheta })\cap L_{\vartheta }(\varvec{a}^*_{\vartheta })$, where $I_{\eta }(\varvec{a}^*_{\vartheta })$ is the indifference curve of type $\eta$ that passes though the type-specific individual allocation $\varvec{a}^*_{\vartheta }$ and $L_{\vartheta }(\varvec{a}^*_{\vartheta })$ is the lower contour set of type $\vartheta$ associated with $\varvec{a}^*_{\vartheta }$. Similarly, by $u_{\vartheta }(\varvec{a}^*_{\vartheta })=u_{\vartheta }(\varvec{a}^*_{\zeta })$ and $u_{\eta }(\varvec{a}^*_{\eta })> u_{\eta }(\varvec{a}^*_{\zeta })$, we have that $\varvec{a}^*_{\zeta }\in I_{\vartheta }(\varvec{a}^*_{\vartheta })\cap L_{\eta }(\varvec{a}^*_{\eta })$.

Therefore, by $u_{\zeta }(\varvec{a}^*_{\eta })= u_{\zeta }(\varvec{a}^*_{\zeta })$, we have that $I_{\zeta }(\varvec{a}^*_{\zeta })$ passes through two points, $\varvec{a}^*_{\eta }$ which belongs in the set $I_{\eta }(\varvec{a}^*_{\vartheta })\cap L_{\vartheta }(\varvec{a}^*_{\vartheta })$, and $\varvec{a}^*_{\zeta }$ which belongs to the set $I_{\vartheta }(\varvec{a}^*_{\vartheta })\cap L_{\eta }(\varvec{a}^*_{\eta })$. But any such indifference curve lies below $\varvec{a}^*_{\vartheta }$, which means that $I_{\zeta }(\varvec{a}^*_{\zeta })\in L_{\zeta }(\varvec{a}^*_{\vartheta })$, which implies that $u_{\zeta }(\varvec{a}^*_{\vartheta })>u_{\zeta }(\varvec{a}^*_{\zeta })$ (see figure 3 for an illustration of the argument when $L=2$). This violates the assumption that all three types belong to the same envy set and hence this case is also impossible to hold. Therefore, it must be that $u_{\vartheta }(\varvec{a}^*_{\vartheta })> u_{\vartheta }(\varvec{a}^*_{\zeta })$. $\square$

The result of Lemma 3 means that rule 2 in page 10, which is used in creating the ranking of types, is transitive. This is because, whenever the conditions of Lemma 3 apply to a triplet of types $\{\vartheta ,\eta ,\zeta \}$, then, as we proved $u_{\vartheta }(\varvec{a}^*_{\vartheta })>u_{\vartheta }(\varvec{a}^*_{\zeta })$, and $u_{\vartheta }(\varvec{a}^*_{\vartheta })>u_{\vartheta }(\varvec{a}^*_{\eta })$. As a result, rule 2 gives higher ranking to type $\vartheta$ over $\eta$ and $\zeta$ and higher ranking to $\eta$ over $\zeta$. Thus, the ranking of types is consistent whenever the rules of page 10 are applied.

Fig. 3

The argument in the proof of Lemma 3 for the case of two goods

1.4 Proof of Theorem 1

Because the set of type-specific individual allocations $\{\varvec{a}^*_{\vartheta }| \vartheta \in \varvec{\Uptheta }\}$ and the corresponding number of bundles which constitute $\varvec{a}^*(\varvec{\omega })$ is independent of $\varvec{\omega }$, the implementation of an efficient allocation rule $\varvec{\rho }^*(\varvec{\omega })=\varvec{a}^*(\varvec{\omega })$ is equivalent to inducing agents to report their type truthfully and to receive the $\varvec{a}^*_{\vartheta }$ that corresponds to their type. Thus, to prove Theorem 1, it is sufficient to find a mechanism that induces agents to reveal their type truthfully and which allocates to them the corresponding $\varvec{a}^*_{\vartheta }$. The proof is done by construction. A sequential mechanism is presented and shown to generate this result. To facilitate its presentation, the proof is broken into several steps, which are summarized in Lemmas.

First, we reintroduce some notation used in the main text along with some new definitions, which are needed exclusively for the proof. Then, the mechanism is presented in formal terms. Subsequently, we provide a series of results on the best-responses of different types at different stages of the mechanism. Finally, these results are put together to provide the final result.

The following list contains the notation and definitions used in the proof of the results that follow:

• $\varvec{a}^*(\varvec{\omega })$ is the first-best and anonymous allocation to be implemented for every $\varvec{\omega }\in \varOmega (\varvec{\phi })$

• The sequence of natural numbers $\{1,2,\ldots ,\vartheta ,\ldots ,\varTheta \}$ represents the sequence of types, which are ranked according to envy and by applying the rules of page 10. Note that this sequence is invariant of $\varvec{\omega }$

• After removing element $\varTheta$, the sequence $\{1,2,\ldots ,\vartheta ,\ldots ,\varTheta -1\}$ also represents the stages of the mechanism. Thus, stage $\vartheta$ refers to the $\vartheta$-th stage of the mechanism, and the “target” type of the stage refers to type $\vartheta$, the agents of which are expected to reveal their type truthfully at this stage

• The sequence $\{\varvec{a}^*_{1},\varvec{a}^*_{2},\ldots ,\varvec{a}^*_{\vartheta },\ldots , \varvec{a}^*_{\varTheta }\}$ is the sequence of first-best type-specific individual allocations which corresponds to the sequence of types $\{1,2,\ldots ,\vartheta ,\ldots ,\varTheta \}$. Note that this sequence is invariant of $\varvec{\omega }$ too

• The sequence $\{\hat{A}(\varvec{a}^*_{1}), \hat{A}(\varvec{a}^*_{2}),\ldots , \hat{A}(\varvec{a}^*_{\vartheta }),\ldots , \hat{A}(\varvec{a}^*_{\varTheta })\}$ is the sequence of self-selective sets, which satisfy the properties of Lemma 2, and each one of them contains type-specific individual allocations in an $\epsilon$-neighborhood of the respective first-best type-specific individual allocation

• $\varvec{\hat{a}}_{\eta }(\varvec{a}^*_{\vartheta })$ denotes a generic element in the self-selective set $\hat{A}(\varvec{a}^*_{\vartheta })$, where $\eta$ denotes the type who prefers this type-specific individual allocation over all others in the set, and $\varvec{a}^*_{\vartheta }$ denotes the first-best type-specific individual allocation, in the $\epsilon$-neighborhood of which $\varvec{\hat{a}}_{\eta }(\varvec{a}^*_{\vartheta })$ is located

• Let $\overline{\varvec{a}}_{\eta }(\vartheta )= \{\varvec{\hat{a}}_{\eta }(\varvec{a}^*_{\zeta })~|~~u_{\eta }(\varvec{\hat{a}}_{\eta }(\varvec{a}^*_{\zeta })) \ge u_{\eta }(\varvec{\hat{a}}_{\eta }(\varvec{a}^*_{\iota }))~,~~\forall ~~\iota \in \varvec{\Uptheta },~\iota \le \vartheta ~,~\vartheta \le \eta \}$ be the self-selective type-specific individual allocation which type $\eta$ prefers over all other in the sequence of self-selective sets up to stage $\vartheta$ of the mechanism. If more than one type-specific individual allocations satisfy this definition, then let $\overline{\varvec{a}}_{\eta }(\vartheta )$ be an arbitrary one among them

• Finally, recall the following definitions from Sect. 3.6. $m_{i\vartheta }$ denotes the “message” or “report” that agent i sends to the mechanism designer at stage $\vartheta$ of the mechanism. $\mu (\vartheta )=\{\# i~|~ \mu _{i \vartheta }=\vartheta , i\in \mathcal {N}\}$ is the total number of agents who report type $\vartheta$. $N(\vartheta )$ is the total number of agents in the economy with type $\vartheta$, which is common knowledge since $N(\vartheta )=\phi (\vartheta )N$.  $J_{\vartheta }$ is the set of agent who participate at stage $\vartheta$.  $g_{i\vartheta }(m_{i\vartheta }, \varvec{m}_{-i,\vartheta })$ is the type-specific individual allocation that the mechanism specifies to agent i as a function of the message profile $\varvec{m}_{\vartheta }=\{m_{i\vartheta }, \varvec{m}_{-i,\vartheta }\}$ if i exits the mechanism at stage $\vartheta$.

Lemma 4

The following results are direct implications of the definition of $\overline{a}_{\eta }(\vartheta )$

• (i) $u_{\eta }(\overline{\varvec{a}}_{\eta }(\vartheta ))> u_{\eta }(\varvec{\hat{a}}_{\zeta }(\varvec{a}^*_{\iota }))~,~\forall ~\varvec{\hat{a}}_{\zeta }(\varvec{a}^*_{\iota })\in \hat{A}(\varvec{a}^*_{\iota })~,~~\forall ~\zeta \ne \eta ,$ $~~\forall ~\iota \le \vartheta$

• (ii) $\overline{\varvec{a}}_{\eta }(\eta )=\varvec{a}^*_{\eta }$

• (iii) $u_{\eta }(\overline{\varvec{a}}_{\eta }(\vartheta ))>u_{\eta }(\overline{\varvec{a}}_{\zeta }(\vartheta )),~~\forall ~\{\zeta ,\eta \}\in \varvec{\Uptheta }$ , $\zeta \ge \vartheta ~,~\eta \ge \vartheta ~,~\zeta \ne \eta$

• (iv) $u_{\eta }(\overline{\varvec{a}}_{\eta }(\zeta )) \ge u_{\eta }(\overline{\varvec{a}}_{\eta }(\vartheta )),~~\forall ~\zeta >\vartheta$

Proof

(i) $u_{\eta }(\varvec{\hat{a}}_{\eta }(\varvec{a}^*_{\iota }))>u_{\eta }(\varvec{\hat{a}}_{\zeta }(\varvec{a}^*_{\iota }))$, $~\forall ~\zeta \ne \eta ,$ $~\forall ~\iota \le \vartheta$, by property (ii) of Lemma 2. Moreover, $u_{\eta }(\overline{\varvec{a}}_{\eta }(\vartheta ))\ge u_{\eta }(\varvec{\hat{a}}_{\eta }(\varvec{a}^*_{\iota }))$, $~\forall ~\iota \le \vartheta$, by the definition of $\overline{\varvec{a}}_{\eta }(\vartheta )$. These two inequalities together imply the result.

(ii) By the design of the self-selective set $\hat{A}(\varvec{a}^*_{\eta })$,  $\varvec{a}^*_{\eta }$ is the most preferable type-specific individual allocation for type $\eta$ among all other elements in this set. In addition, for $\vartheta <\eta$, property (iv) of Lemma 2 and the definition of $\varvec{\hat{a}}_{\eta }(\varvec{a}^*_{\vartheta })$ mean that $\varvec{a}^*_{\eta }$ is strictly preferred to any other element of any self-selective set $\hat{A}(\varvec{a}^*_{\vartheta })$. These two facts together imply the result.

(iii) By construction, $\overline{\varvec{a}}_{\zeta }(\vartheta )$ is one of the type-specific individual allocations in the sequence $\{\varvec{\hat{a}}_{\zeta }(\varvec{a}^*_1), \varvec{\hat{a}}_{\zeta }(\varvec{a}^*_2),\ldots ,\varvec{\hat{a}}_{\zeta }(\varvec{a}^*_{\vartheta })\}$. Suppose it is the $\iota$-th element in this sequence, with $1 \le \iota \le \vartheta$. Then, by property (ii) of Lemma 2 and the definition of $\overline{\varvec{a}}_{\eta }(\vartheta )$, we have that,  $u_{\eta }(\overline{\varvec{a}}_{\zeta }(\vartheta )) = u_{\eta } (\varvec{\hat{a}}_{\zeta }(\varvec{a}^*_{\iota }))<u_{\eta }(\varvec{\hat{a}}_{\eta }(\varvec{a}^*_{\iota })) \le u_{\eta }( \overline{\varvec{a}}_{\eta }(\vartheta ))$.

(iv):

$\overline{\varvec{a}}_{\eta }(\vartheta )= argmax\{ u_{\eta }(\varvec{a}_{\iota }) ~|~ \varvec{a}_{\iota } \in \{\varvec{\hat{a}}_{\eta }(\varvec{a}^*_1), \varvec{\hat{a}}_{\eta }(\varvec{a}^*_2),\ldots ,\varvec{\hat{a}}_{\eta }(\varvec{a}^*_{\vartheta })\} ~\}$ $\overline{\varvec{a}}_{\eta }(\zeta )= argmax\{ u_{\eta }(\varvec{a}_{\iota }) ~|~ \varvec{a}_{\iota } \in \{\varvec{\hat{a}}_{\eta }(\varvec{a}^*_1), \varvec{\hat{a}}_{\eta }(\varvec{a}^*_2),\ldots ,\varvec{\hat{a}}_{\eta }(\varvec{a}^*_{\zeta })\} ~\}$ $\{\varvec{\hat{a}}_{\eta }(\varvec{a}^*_1), \varvec{\hat{a}}_{\eta }(\varvec{a}^*_2),\ldots ,\varvec{\hat{a}}_{\eta }(\varvec{a}^*_{\vartheta })\} \subseteq \{\varvec{\hat{a}}_{\eta }(\varvec{a}^*_1), \varvec{\hat{a}}_{\eta }(\varvec{a}^*_2),\ldots ,\varvec{\hat{a}}_{\eta }(\varvec{a}^*_{\zeta })\}$

therefore $u_{\eta }(\overline{\varvec{a}}_{\eta }(\zeta )) \ge u_{\eta }(\overline{\varvec{a}}_{\eta }(\vartheta ))$. $\square$

The mechanism $\varvec{M^*}$ We denote the mechanism by $M^*$ to separate it from all other possible mechanisms. It consists of $\varTheta -1$ stages. In each stage $\vartheta$, $1\le \vartheta \le \varTheta -1$ each agent i who participates in the stage sends a report $m_{i\vartheta }\in \{\vartheta , \vartheta +1,\ldots ,\varTheta \}$. That is, the strategy space of each agent is a report of a type at least as large in terms of ranking as the stage of the mechanism.

At an arbitrary stage $\vartheta$,  $1\le \vartheta \le \varTheta -2$,  if $~\mu (\vartheta )=N(\vartheta )~$, then agents with $m_{i \vartheta }=\vartheta$ receive the first-best type-specific individual allocation $\varvec{a}^*_{\vartheta }$ and exit the mechanism that is they consume $\varvec{a}^*_{\vartheta }$ immediately and they do not play in the remaining stages of the mechanism. The remaining agents, that is agents with $m_{i \vartheta }\ne \vartheta$, move to stage $\vartheta +1$ of the mechanism. If $\mu (\vartheta )\ne N(\vartheta )$, then the mechanism ends at stage $\vartheta$ and each agent with $m_{i \vartheta }=\eta$, $\vartheta \le \eta \le \varTheta$, receives and consumes the type-specific individual allocation $\overline{\varvec{a}}_{\eta }(\vartheta )$.

If the mechanism reaches stage $\varTheta -1$, the last stage possible, then, if $\mu (\varTheta -1)=N(\varTheta -1)$ agents with $m_{i, \varTheta -1}=\varTheta -1$ receive and consume type-specific individual allocation $\varvec{a}^*_{\varTheta -1}$, agents with $m_{i, \varTheta -1}=\varTheta$ receive and consume type-specific individual allocation $\varvec{a}^*_{\varTheta }$, and the mechanism ends. If $\mu (\varTheta -1)\ne N(\varTheta -1)$, then agents with $m_{i, \varTheta -1}=\varTheta -1$ receive and consume type-specific individual allocation $\varvec{a}^*_{\varTheta -1}$, agents with $m_{i, \varTheta -1}=\varTheta$ receive and consume type-specific individual allocation $\overline{\varvec{a}}_{\varTheta }(\varTheta -1)$, and the mechanism ends. Formally, we have the following description of the mechanism $M^*$.

• For all $\vartheta$ such that $1\le \vartheta \le \varTheta -2$:

  • If $\mu (\vartheta )=N(\vartheta )$, then for all $i\in \{m_{i\vartheta }=\vartheta \}:~ g_{i\vartheta }(\vartheta ,\varvec{m}_{-i,\vartheta })=\varvec{a}^*_{\vartheta }~,~i\notin J_{\vartheta +1}$ , and for all $i\in \{m_{i\vartheta }=\eta \ne \vartheta \}:~ g_{i\vartheta }(\eta ,\varvec{m}_{-i,\vartheta })=\emptyset ~,~i\in J_{\vartheta +1}$

  • If $\mu (\vartheta )\ne N(\vartheta )$, then for all $i\in \{m_{i\vartheta }=\eta \}:~ g_{i\vartheta }(\eta ,\varvec{m}_{-i,\vartheta })=\overline{\varvec{a}}_{\eta }(\vartheta )$, for all $\eta \in \{\vartheta , \vartheta +1,\ldots ,\varTheta \}$, and $J_{\vartheta +1}=\emptyset$,

• For $\vartheta =\varTheta -1$:

  • If $\mu (\varTheta -1)=N(\varTheta -1)$, then for all $i\in \{m_{i,\varTheta -1}=\varTheta -1\}:~ g_{i,\varTheta -1}(\varTheta -1,\varvec{m}_{-i,\varTheta -1})=\varvec{a}^*_{\varTheta -1}$ , for all $i\in \{m_{i,\varTheta -1}= \varTheta \}:~ g_{i,\varTheta -1}(\varTheta ,\varvec{m}_{-i,\varTheta -1})=\varvec{a}^*_{\varTheta }$, and $J_{\varTheta }=\emptyset$

  • If $\mu (\varTheta -1)\ne N(\varTheta -1)$, then for all $i\in \{m_{i,\varTheta -1}=\eta \}:~ g_{i,\varTheta -1}(\eta ,\varvec{m}_{-i,\varTheta -1})=\overline{\varvec{a}}_{\eta }(\varTheta -1)$, for all $\eta \in \{\varTheta -1,\varTheta \}$, and $J_{\varTheta }=\emptyset$

Lemma 5

Under $M^*$, at any stage $\vartheta , 1\le \vartheta \le \varTheta -1$, it is a strictly dominated strategy for any agent of type $\eta$, with $\eta >\vartheta$, to report type $\vartheta$.

Proof

Consider a generic stage $\vartheta , 1\le \vartheta \le \varTheta -1$, and an agent i with a generic type $\eta , \vartheta <\eta \le \varTheta$. We show that the strategy $m_{i\vartheta }=\vartheta$ is strictly dominated by the strategy $m_{i\vartheta }=\eta$, which is the truth-telling strategy, irrespective of i’s beliefs whether the mechanism ends in stage $\vartheta$ or not.

In terms of how i’s strategy affects the probability that the mechanism terminates at stage $\vartheta$, there are three cases to consider. These three cases correspond to all the possible ways that the other agents’ messages affect i’s payoff.

• (a) When all other agents reports, excluding i’s report, are such $\mu (\vartheta )=N(\vartheta )$

• (b) When all other agents reports, excluding i’s report, are such $\mu (\vartheta )\ge N(\vartheta )+1$ or $\mu (\vartheta )< N(\vartheta )-1$

• (c) When all other agents reports, excluding i’s report, are such $\mu (\vartheta )= N(\vartheta )-1$

(a) In this case i believes that the reports of the remaining agents are such that the number of agents who report type $\vartheta$ is exactly equal to the number of agents with type $\vartheta$, given by the realized distribution of types $\varvec{\phi }$. i is pivotal for the outcome of the mechanism in this case. If i reports type $\vartheta$, then she increases $\mu (\vartheta )$ by one, so that, after including i’s report, $\mu (\vartheta )=N(\vartheta )+1 \ne N(\vartheta )$, which induces the mechanism to end at stage $\vartheta$. If, on the other hand, i reports truthfully her type $\eta$, then $\mu (\vartheta )$ remains unchanged after including her report. The mechanism proceeds to stage $\vartheta +1$, and i along with it, since only agents with strategies $m_{j\vartheta }=\vartheta , j\ne i$, exit the mechanism at stage $\vartheta$.

From the above two outcomes, i strictly prefers the second, which corresponds to the strategy $m_{i\vartheta }=\eta$, over the first, which corresponds to the strategy $m_{i\vartheta }=\vartheta$. To reach this conclusion, we first note that if i plays $m_{i\vartheta }=\vartheta$, then the mechanism terminates at stage $\vartheta$ and, by its rules, i receives and consumes $\overline{\varvec{a}}_{\vartheta }(\vartheta )$, which is equal to $\varvec{a}^*_{\vartheta }$ by Lemma 4(ii). If, on the other hand, i plays $m_{i\vartheta }=\eta$, her continuation payoff is at least as large $u_{\eta }(\overline{\varvec{a}}_{\eta }(\vartheta ))$. The last argument is true because, by Lemma 4(iv), $u_{\eta }(\overline{\varvec{a}}_{\eta }(\zeta ))\ge u_{\eta }(\overline{\varvec{a}}_{\eta }(\vartheta )),~~\forall ~\zeta >\vartheta$. Finally, because $u_{\eta }(\overline{\varvec{a}}_{\eta }(\vartheta ))>u_{\eta }(\overline{\varvec{a}}_{\vartheta }(\vartheta ))= u_{\eta }(\varvec{a}^*_{\vartheta })$ by Lemma 4(iii), reporting truthfully and proceeding to stage $\vartheta +1$ is strictly preferable to i than terminating the mechanism at stage $\vartheta$.

(b) In the second case i believes that the reports of the remaining agents are such that the number of agents who report type $\vartheta$ does not equal the number of agents with type $\vartheta$, irrespective of her own report. That is, i expects that $\mu (\vartheta )\ne N(\vartheta )$ for all her strategies $m_{i\vartheta }$, and, therefore, she believes that the mechanism terminates at stage $\vartheta$ and she cannot affect this outcome. Under this belief, i expects to receive and consume $\overline{\varvec{a}}_{\eta }(\vartheta )$ if she reports $\eta$ and she expects to receive and consume $\overline{\varvec{a}}_{\vartheta }(\vartheta )$ if she reports $\vartheta$. By Lemma 4, $u_{\eta }(\overline{\varvec{a}}_{\eta }(\vartheta ))>u_{\eta }(\overline{\varvec{a}}_{\vartheta }(\vartheta ))= u_{\eta }(\varvec{a}^*_{\vartheta })$, and therefore, i strictly prefers to report truthfully than to report type $\vartheta$.

(c) In the last case i believes that the reports of the remaining agents are such that the number of agents who report type $\vartheta$ does not equal the number of agents with type $\vartheta$ by only one. If i reports $\vartheta$, then, including her report, $\mu (\vartheta )= N(\vartheta )$ and so the mechanism does not terminate at stage $\vartheta$. If i reports $\eta$, then $\mu (\vartheta )\ne N(\vartheta )$ and the mechanism terminates at stage $\vartheta$. Therefore i’s report is pivotal in determining the outcome of the mechanism for the other agents. For i, however, the comparison of payoffs is the same as in case (b). If i reports $\vartheta$, then she receives and consumes $\varvec{a}^*_{\vartheta }$ and exits the mechanism. If, on the other hand, she reports $\eta$ the mechanism terminates at stage $\vartheta$ and she receives and consumes $\overline{\varvec{a}}_{\eta }(\vartheta )$. As in case (b), $u_{\eta }(\overline{\varvec{a}}_{\eta }(\vartheta ))>u_{\eta }(\varvec{a}^*_{\vartheta })$, by Lemma 4, and therefore i strictly prefers to report truthfully.

Overall, under all possible beliefs regarding the outcomes of the mechanism, i strictly prefers reporting her type truthfully over reporting type $\vartheta$, and, therefore, the last strategy is strictly dominated for her and will never be played in any equilibrium of the mechanism. $\square$

Lemma 6

If stage $\vartheta$ of $M^*$ is reached, $\vartheta >1$, then all agents with types of rank lower than type $\vartheta$ have exited the mechanism at previous stages, and all agents with types of rank equal or higher than $\vartheta$ participate in stage $\vartheta$.

Proof

The proof is done by induction. Consider stage 1 of $M^*$. By the design of $M^*$, moving from stage 1 to stage 2 happens only if $\mu (1)=N(1)$. Since, by Lemma 5, all agent with types $\{2,3,\ldots \varTheta \}$ do not report type 1 at stage 1, the requirement for proceeding to stage 2 is met only if all agents with type 1 report their type truthfully and exit the mechanism at stage 1. Therefore, if stage 2 is reached, all the agents of type 2 or higher participate, but no agent of type 1 participates.

Similarly, stage 3 is reached only if $\mu (2)=N(2)$ at stage 2. By Lemma 5, no agent of type 3 or of higher type reports type 2 so stage 3 is reached only if all agents of type 2 report their type truthfully. Thus, if stage 3 is reached, then all agents of type 2 have exited at stage 2 and all agents of type 3 or higher participate in stage 3. By applying the same reasoning to each successive stage, the result obtains. $\square$

Lemma 7

Under $M^*$, the unique best-response of any agent with type $\vartheta$ when she participates in stage $\vartheta$ is to report her type truthfully.

Proof

By Lemma 6, in stage $\vartheta$ participate all agents of type $\vartheta$ or higher and no agent of rank lower than $\vartheta$. By Lemma 5, all agents of type $\vartheta +1$ or higher do not report type $\vartheta$. Therefore, for an agent i of type $\vartheta$ there are two distinct sets of beliefs consistent with the equilibrium behavior of other types.

• (a) When all other agents of type $\vartheta$ report truthfully

• (b) When one or more agents of type $\vartheta$ do not report truthfully

(a) In this case, excluding i’s report, $\mu (\vartheta )=N(\vartheta )-1$. If i reports $m_{i\vartheta }=\vartheta$, then, after including her report, $\mu (\vartheta )$ increases by one so that $\mu (\vartheta )=N(\vartheta )$, the mechanism proceeds to stage $\vartheta +1$ if $\vartheta <\varTheta -1$ or terminates if $\vartheta =\varTheta -1$, and i receives and consumes $\varvec{a}^*_{\vartheta }$. If i reports $m_{i\vartheta }=\eta \ne \vartheta$, then, after including her report, $\mu (\vartheta )<N(\vartheta )$, the mechanism terminates at stage $\vartheta$, and i receives and consumes $\overline{\varvec{a}}_{\eta }(\vartheta )$. By Lemma 4, $u_{\vartheta }(\varvec{a}^*_{\vartheta })=u_{\vartheta }(\overline{\varvec{a}}_{\vartheta }(\vartheta )) >u_{\vartheta }(\overline{\varvec{a}}_{\eta }(\vartheta )$, therefore, i strictly prefers to report truthfully than to report any other type.

(b) In this case, excluding i’s report, $\mu (\vartheta ) \le N(\vartheta )-2$, and, therefore, irrespective of i’s report, the mechanism terminates at stage $\vartheta$. If i reports $m_{i\vartheta }=\vartheta$ she receives and consumes $\overline{\varvec{a}}_{\vartheta }(\vartheta )=\varvec{a}^*_{\vartheta }$ and if she reports $m_{i\vartheta }=\eta \ne \vartheta$, then she receives and consumes $\overline{\varvec{a}}_{\eta }(\vartheta )$. As with case (a) above, $u_{\vartheta }(\overline{\varvec{a}}_{\vartheta }(\vartheta )) >u_{\vartheta }(\overline{\varvec{a}}_{\eta }(\vartheta )$, and, therefore, i strictly prefers to report truthfully than to report any other type.

Overall, under any set of beliefs regarding the possible strategies of the other agents with type $\vartheta , i$ strictly prefers to report truthfully than report any other type and the result of the Lemma obtains. $\square$

Together, the construction of $M^*$ along with the results of Lemmas 5, 6 and 7, implies the result of Theorem 1 in page 12. To be precise, at any stage $\vartheta$ of $M^*$,  $1\le \vartheta \le \varTheta -1$,  agents of type with rank higher than $\vartheta$ do not report type $\vartheta$, by Lemma 5, agents of type with rank lower than $\vartheta$ have exited the mechanism at earlier stages, by Lemma 6, and the unique best-response of agents with type $\vartheta$ is to report their type truthfully, receive $\varvec{a}^*_{\vartheta }$ and exit the mechanism, by Lemma 7.

The result of Lemma 7 also implies that, since $\mu (\vartheta )=N(\vartheta )$, $1\le \vartheta \le \varTheta -1$, on the equilibrium path, all stages of the mechanism are reached. Moreover, since Lemmas 5 and 7 apply to the last stage as well, stage $\varTheta -1$, then $\mu (\varTheta -1)=N(\varTheta -1)$. Therefore, by the design of $M^*$, all agents of type $\varTheta -1$ receive and consume $\varvec{a}^*_{\varTheta -1}$, all agents of type $\varTheta$ receive and consume $\varvec{a}^*_{\varTheta }$ and the mechanism terminates. Thus, the unique perfect Bayesian equilibrium outcome of $M^*$ is for all agents to report their type truthfully and to receive the first-best type-specific individual allocation corresponding to their type, as Theorem 1 requires. $\square$