Abstract
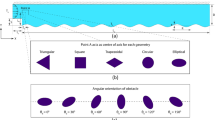
Shock-wave propagation through different arrays of solid obstacles and its attenuation are analyzed by means of numerical simulations. The two-dimensional compressible Navier–Stokes equations are solved using a fifth-order weighted essentially non-oscillatory scheme, in conjunction with an immersed-boundary method to treat the embedded solids within a cartesian grid. The present study focuses on the geometrical aspects of the solid obstacles, particularly at lower effective flow area, where the frictional forces are expected to be important. The main objective is to analyze the controlling mechanism for shock propagation and attenuation in complex inhomogeneous and porous medium. Different parameters are investigated such as the geometry of the obstacles, their orientation in space as well as the relaxation lengths between two consecutive columns. The study highlights a number of interesting phenomena such as compressible vortices and shock–vortex interactions that are produced in the post-shock region. This also includes shock interactions, hydrodynamic instabilities and non-linear growth of the mixing. Ultimately, the Kelvin–Helmholtz instability invokes transition to a turbulent mixing region across the matrix columns and eddies of different length scales are generated in the wake region downstream of the solid blocks. The power spectrum of instantaneous dynamic pressure shows the existence of a wide range of frequencies which scales nearly with f −5/3. In terms of shock attenuation, the results indicate that the staggered matrix of reversed triangular prism (where the base of the triangular prism is facing the incoming shock) is the most efficient arrangement. In this case, both static and dynamic pressure impulses show significant reduction compared to the other studied configurations, which confirms the effectiveness of this type of barrier configuration. Furthermore, the use of combination of reverse–reverse arrangement of triangular prism obstacle maze is found more effective compared to the forward–reverse or forward–forward arrangements.
Similar content being viewed by others
References
Vasilev E.I., Mitichkin S.Yu., Testov V.G., Haibo H.: Pressure dynamics during shock loading of aqueous foams. Tech. Phys. 43(7), 761–765 (1998)
Ball G.J., East R.A.: Shock and blast attenuation by aqueous foam barriers: influences of barrier geometry. Shock Waves 9, 37–47 (1999)
Surov V.S.: Reflection of an air shock wave from a foam layer. High Temp. 38(1), 97–105 (2000)
Britan A., Ben-Dor G., Shapiro H., Liverts M., Shreiber I.: Drainage effects on shock wave propagating through aqueous foams. Colloids Surf. A Physicochem. Eng. Aspects 309, 137150 (2007)
Jourdan G., Biamino L., Mariani C., Blanchot C., Daniel E., Massoni J., Houas L., Tosello R., Praguine D.: Attenuation of a shock wave passing through a cloud of water droplets. Shock Waves 20, 285296 (2010)
Hattingh T.S., Skews B.W.: Experimental investigation of the interaction of shock waves with textiles. Shock Waves 11, 115–123 (2001)
Gubaidullin A.A., Dudko D.N., Urmancheev S.F.: Modeling of the interaction between an air shock wave and a porous screen. Combust. Explos. Shock Waves 36(4), 496–505 (2000)
Gubaidullin A.A., Britan A., Dudko D.N.: Air shock wave interaction with an obstacle covered by porous material. Shock Waves 13, 41–48 (2003)
Boldyreva O.Yu., Gubaidullin A.A., Dudko D.N., Kutushev A.G.: Numerical study of the transfer of shock-wave loading to a screened flat wall through a layer of a powdered medium and a subsequent air gap. Combust. Explos. Shock Waves 43(1), 114–123 (2007)
Britan A., Ben-Dor G., Igra O., Shapiro H.: Shock waves attenuation by granular filters. Int. J. Multiph. Flow 27, 617–634 (2001)
Bakken J., Slungaard T., Engebretsen T., Christensen S.O.: Attenuation of shock waves by granular filters. Shock Waves 13, 33–40 (2003)
Andreopoulos Y., Xanthos S., Subramaniam K.: Moving shocks through metallic grids: their interaction and potential for blast wave mitigation. Shock Waves 16, 455–466 (2007)
Sasoh A., Matsuoka K., Nakashio K., Timofeev E., Takayama K., Voinovich P., Saito T., Hirano S., Ono S., Makino Y.: Attenuation of weak shock waves along pseudo-perforated walls. Shock Waves 8, 149–159 (1998)
Britan A., Karpov A.V., Vasiev E.I., Igra O., Ben-Dor G., Shapiro E.: Experimental and numerical study of shock wave interaction with perforated plates. J. Fluids Eng. 126, 399–409 (2004)
Britan A., Igra O., Ben-Dor G., Shock H.: wave attenuation by grids and orifice plates. Shock Waves 16, 1–15 (2006)
Seeraj S., Skews B.W.: Dual-element directional shock wave attenuators. Exp. Thermal Fluid Sci. 33, 503–516 (2009)
Rogg B., hermann D., Adomeit G.: Shock-induced flow in regular arrays of cylinders and packed beds. Int. J. Heat Mass Transf. 28(12), 2285–2298 (1985)
Skews B.W., Draxl M.A., Felthun L., Seitz M.W.: Shock wave trapping. Shock Waves 8, 23–28 (1998)
Suzuki, K., Himeki, H., Watanuki, T., Abe, T.: Experimental studies on characteristics of shock wave propagation through cylinder array, The ISAS Report No. 676, March (2000)
Abe, A., Takayama, K.: Attenuation of shock waves propagating over arrayed spheres. In: Takayama, K., Saito, T., Kleine, H., Timofeev, E. (eds.) Proceedings of 24th International Congress High-Speed Photography and Photonic, Sendai, Japan: SPIE The international Society for Optical Engineering 582588 (2000)
Honghui, S., Yamamura, K.: The interaction between shock waves and solid spheres arrays in a shock tube. Acta Mech. Sinica 20, 3 (2004)
Friend, W.H.: The interaction of a plane shock with an inclined perforated plate. UTIA Technical Note 25 (1958)
Wilson, J., Chima, R.V., Skews, B.W.: Transmission and incidence losses for a slotted plate, NASA/TM1998-207420
Berger S., Sadot O., Ben-Dor G.: Experimental investigation on the shock-wave load attenuation by geometrical means. Shock waves 20(1), 29–40 (2010)
Naiman H., Knight D.D.: The effect of porosity on interaction with a rigid, porous barrier. Shock Waves 16, 321–337 (2007)
Chaudhuri A., Hadjadj A., Chinnayya A.: On the use of immersed boundary methods for shock/obstacle interactions. J. Comput. Phys. 230, 1731–1748 (2011)
Glazer E., Sadot O., Hadjadj A., Chaudhuri A.: Velocity scaling of a shock wave reflected off a circular cylinder. Phys. Rev. E 83, 066317 (2011)
Chaudhuri, A., Hadjadj, A., Sadot, O., Glazer, E.: Computational study of shock-wave interaction with solid obstacles using immersed boundary methods. Int. J. Num. Method Eng. doi:10.1002/nme.3271 (2011)
Jiang G., Shu C.W.: Efficient implementation of weighted ENO schemes. J. Comput. Phys. 126, 202–228 (1996)
Peskin, C.S.: Flow patterns around heart valves: a digital computer method for solving the equations of motion, PhD thesis, Physiol., Albert Einstein Coll. Med., vol. 378, pp. 72–30, Univ. Microfilms (1972)
Mittal R., Iaccarino G.: Immersed boundary methods. Annu. Rev. Fluid Mech. 37, 239–261 (2005)
Iaccarino G., Verzicco R.: Immersed boundary technique for turbulent flow simulations. Appl. Mech. Rev. 56, 331–347 (2003)
Tseng Y., Ferziger J.H.: A ghost-cell immersed boundary method for flow in complex geometry. J. Comput. Phys. 192, 593–623 (2003)
Gao T., Tseng Y., Lu X.: An improved hybrid cartesian/immersed boundary method for fluid-solid flows. Int. J. Numer. Meth. Fluids 55, 1189–1211 (2007)
Dadone A., Grossman B.: Ghost-cell method for inviscid two-dimensional flows on cartesian grids. AIAA J. 42(12), 2499–2507 (2004)
Chaudhuri A., Hadjadj A., Chinnayya A., Palerm S.: Numerical study of compressible mixing layers using high-order WENO schemes. J. Sci. Comput. 47(2), 170–197 (2011). doi:10.1007/s10915-010-9429-3
Whitham G.B.: A new approach to problems of shock dynamics. Part I: two-dimensional problems. J. Fluid Mech. 2, 145–171 (1957)
Schardin H.: High frequency cinematography in the shock tube. J. Photo Sci. 5, 19–26 (1957)
Bryson A.E., Gross R.W.F.: Diffraction of strong shocks by cones, cylinders, and spheres. J. Fluid Mech. 10, 1–16 (1961)
Skews B.W.: The shape of diffraction shock wave. J. Fluid Mech. 29, 297–304 (1967)
Yang J.Y., Liu Y., Lomax H.: Computation of shock wave reflection by circular cylinders. AIAA J. 25(5), 683–689 (1987)
Kaca, J.: An interferometric investigation of the diffraction of a planar shock wave over a semicircular cylinder (UTIAS Technical Note), vol. 269 (1988)
Hillier R.: Computation of shock wave diffraction at a ninety degree convex edge. Shock waves 1, 89–98 (1991)
Sivier S., Loth E., Baum J., Lohner R.: Vorticity produced by shoch wave diffraction. Shock waves 2, 31–41 (1992)
Reichenbach H.: In the footsteps of Ernst Mach—a historical review of shock wave research at the Ernst-MAch-Institut. Shock waves 2, 65–79 (1992)
Zoltak J., Drikakis D.: Hybrid upwind methods fir the simulation of unsteady shock-wave diffraction over a cylinder. Comput. Methods Appl. Mech. Eng. 162, 165–185 (1998)
Chang S., Chang K.: On the shock–vortex interaction in Schardin’s problem. Shock Waves 10, 333–343 (2000)
Rikanati, A., Sadot, O., Ben-Dor, G., Shvarts, D., Kuribayashi, T., Takayama, K.: Shock-Wave Mach-reflection slip-stream instability. Phys Rev Lett. 96, 174503 (2006)
Ripley R.C., Lien F.S., Yovanovich M.M.: Numerical simulation of shock diffraction on unstructured meshes. Comput. Fluids 35, 1420–1431 (2006)
Tseng T.-I., Yang R.-J.: Numerical simulation of vorticity production in shock diffraction. AIAA J. 44(5), 1040–1047 (2006)
Ben-Dor G.: Shock Wave Reflection Phenomena, 2nd edn. Springer, Berlin (2007)
Suzuki, K., Himeki, H., Watanuki, T., Abe, T.: Experimental studies on characteristics of shock wave propagation through cylinder array, The Institute of Space and Astronautical Science Report No. 676, March (2000)
Anderson J.D.: Modern Compressible Flow with Historical Perspective. McGraw-Hill, New York (1982)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by C. Needham.
This paper was presented in part at the 28th International Symposium on Shock Waves, Manchester, UK, 17–22 July 2011.
Rights and permissions
About this article
Cite this article
Chaudhuri, A., Hadjadj, A., Sadot, O. et al. Numerical study of shock-wave mitigation through matrices of solid obstacles. Shock Waves 23, 91–101 (2013). https://doi.org/10.1007/s00193-012-0362-2
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00193-012-0362-2