Abstract
We develop a model in which a strategic complementarity in saving decisions arises due to a minimum investment requirement and financial market imperfection. We explore the role of self-fulling beliefs in determining the long run dynamics. The model exhibits a wide range of dynamic phenomena such as a poverty trap, a big push and a sunspot equilibrium, depending on the level of financial market imperfection. They account for excessive volatility and a sudden change in the saving rate and its macroeconomic consequences without any shocks to fundamentals.











Similar content being viewed by others
Notes
The theory predicts that higher income growth causes higher saving rates since consumption reacts slowly to income growth.
The data are obtained from the World Bank Development Indicators. See Appendix C for details.
In contrast, Schmidt-Hebbel et al. (2001) estimates that most of the saving rate movement is unaccounted and only up to 12.2% of the increase in the national saving rate can be attributed to the pension reform. Samwick (2000) provides empirical evidence that the saving rate did not increase in other OECD countries such as Switzerland and Australia, which also reformed their pension systems. Even more, Samwick (2000) concludes, based on cross-country regressions of 94 reforming countries, that pension reforms have significant negative effects on the saving rate. These studies show that pension reforms in different countries have mixed effects.
This is a typical case of a sunspot equilibrium—sunspots coordinate individual decisions—where extrinsic uncertainty matters even in the long run. The technique to use sunspots as coordination devices to choose one equilibrium out of many is presented in Matsuyama (2002). We make use of the theory of the so called random iterated function systems to obtain well defined forward orbits when multiple equilibria exist (e.g. Mitra, Montrucchio and Privileggi 2004, Mitra and Privileggi 2004, Gardini et al. 2009, Mitra and Privileggi 2009), and derive the stationary probability distribution over all possible states.
Matsuyama (2004) analyzes a world economy that consists of identical small open economies, which differ only in their levels of capital stock. In the small open economy, the interest rate does not adjust to equate domestic savings to domestic investment. The financial market imperfection then generates multiple steady states.
See Levine (2005) for discussions on financial development and income distribution.
Capital depreciates fully between periods, so capital stock in the following period is equal to current investment.
The model can be generalized to allow agents to run more than one project. The project size would then expand until the borrowing constraint binds. Critical is the minimum project size of one unit of consumption goods. If this assumption is relaxed, competition would force agents to reduce the project size until the borrowing constraint is not binding.
This can be confirmed by changing λ for a fixed R ∈ (0, R +) in Fig. 3.
If s ∗ > 1 − λ, then λ > ψ 2(R) ensures that the borrowing constraint is not binding in s ∗.
Any stochastic process ensuring a positive probability to each equilibrium at all times t would define a proper IFS. The i.i.d assumption is made only to derive the stationary probability distribution over all the possible states in Section 4.2.
Remember that \(H(s,\lambda ,R)=\frac {\lambda \alpha R^{\alpha }s^{\alpha -1}}{1-s}\), \(s^{c}=\frac {1-\alpha }{2-\alpha }\), and \(s^{*}=[(1-\alpha )R^{\alpha }]^{\frac {1}{1-\alpha }}\).
Notice that α < 1/2 is sufficient to ensure (a).
In Murphy et al. (1989), it is sufficient for firms to expect that there will be demand for their products and to decide to invest in the modern production technology, making their expectation a self-fulling prophecy.
We note that s L is increasing in λ while s M is decreasing in λ. This implies that higher financial market imperfection leads to higher volatility of the saving rates as well as greater inequality in s L but smaller inequality in s M .
The steady state aggregate saving rate \(\frac {s}{f(sR)}\) is increasing in s because f is concave.
Existence of multiple steady states also requires that \(\beta \in (0, \overline {\beta }(\alpha ))\) for any α ∈ (0, 1).
See Benhabib and Farmer (1999) for a survey on econometrics of multiple equilibria in macroeconomics.
Detailed descriptions of the measurement of the data is given in the appendix. Other measures of volatility such as \(\sqrt {\frac {1}{T}{\sum }_{t=0}^{T}(s_{it}-s_{it-1})^{2}}\) equally generate statistically significant results.
Country codes presented in Fig. 10 are: AUS - Australia, AUT - Austria, BEL - Belgium, CAN - Canada, CHL - Chile, CZE - Czech Republic, DNK - Denmark, EST - Estonia, FIN - Finland, FRA - France, DEU - Germany, GRC - Greece, HUN - Hungary, ISL - Iceland, IRL - Ireland, ISR - Israel, ITA - Italy, JPN - Japan, KOR - Korea, Republic, MEX - Mexico, NLD - Netherlands, NZL - New Zealand, NOR - Norway, POL - Poland, PRT - Portugal, SVK - Slovak Republic, SVN - Slovenia, ESP - Spain, SWE - Sweden, CHE - Switzerland, GBR - United Kingdom. The above regression omits Luxembourg as an outlier because σ i takes by far the largest value during the sample period. The quadratic regression remains statistically significant even when including Luxembourg.
Note that our theoretical model does not predict that all countries with an intermediate level of the financial market imperfection necessarily have a high volatility, as the dynamics still depends on the probability attached to each state.
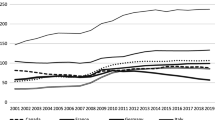
We have dropped Ireland for this example as the saving rate in Ireland shows a clear downward trend during this period.
We have not used the sample average of financial market imperfection during the period 2006 and 2010 as there are too many countries with missing data. This may not be too much of concern as we do not look at the variation within a country but across countries. No clear time trend in financial market imperfection was observed for the selected countries.
References
Acemoglu D, Zilibotti F (1997) Was prometheus unbound by chance? Risk, diversification, and growth. J Policital Econ 105:709–751
Aghion P, Bolton P (1997) A trickle-down theory of growth and development with debt overhang. Rev Econ Stud 64:151–172
Banerjee A, Newman A (1993) Occupational choice and the process of development. J Polictical Econ 101:274–298
Beck T, Demirgüç-Kunt A, Levine R (2007) Finance, inequality and the poor. J Econ Growth 12:27–49
Benhabib J, Farmer R (1999) Indeterminacy and sunspots in macroeconomics. In: Taylor J.B., Woodford M. (eds) Handbook of Macroeconomics, vol 1, pp 387–448
Bulow J, Geanakoplos J, Klemperer P (1985) Multimarket oligopoly: strategic subsitutes and complements. J Polictical Econ 95:488–511
Brueckner M, Kikuchi T, Vachadze G (2017) Economic growth, domestic saving rates and borrowing contraints, mimeo
Cooper R, John A (1988) Coordinating coordination failures in keynesian models. Q J Econ 103:441–463
Galor O, Zeira J (1993) Income distribution and macroeconomics. Rev Econ Stud 60:35–52
Gardini L, Hommes C, Tramontana F, De Vilder R (2009) Forward and backward dynamics in implicitly defined overlapping generations models. J Econ Behav Organ 71:110–129
Gimet C, Lagoarde-Sego T (2011) A closer look at financial development and income distribution. J Bank Finan 37:1698–1713
Guidolin M, La Jeunesse E (2007) The decline in the us personal saving rate: is it real and is it a puzzle? Fed Reserve Bank St. Louis Rev 89:491–514
Iwaisako T, Okada K (2012) Understanding the decline in Japan’s saving rate in the new millennium. Jpn World Econ 24:163–173
Krugman P (1991) History versus expectations. Q J Econ 106:651–667
Levine R (2005) Finance and growth: theory and evidence. In: Aghion P, Durlauf S (eds) Handbook of Economic Growth. 1st edn. Ch. 12, pp 865–934
Li H, Squire L, Zou H (1998) Explaining international and intertemporal variations in income inequality. Econ J 108:26–43
Matsuyama K (1991) Increasing returns, industrialization, and indeterminacy of equilibrium. Q J Econ 106:617–650
Matsuyama K (2002) Explaining diversity: symmetry-breaking in complementarity games. Amerx Econ Rev 92:241–246
Matsuyama K (2004) Financial market globalization, symmetry-breaking, and endogenous inequality of nations. Econometrica 72:853–884
Mitra T, Montrucchio L, Privileggi F (2004) The nature of the steady state in models of optimal growth with uncertainty. Econ Theory 23:39–72
Mitra T, Privileggi F (2004) Cantor type invariant distributions in the theory of optimal growth under uncertainty. J Differ Equ Appl 10:489–500
Mitra T, Privileggi F (2009) On lipschitz continuity of the iterated function system in a stochastic optimal growth model. J Math Econ 45:185–198
Mody A, Ohnsorge F, Sandri D (2012) Precautionary savings in the great recession. IMF Econ Rev 60:114–138
Mookherjee D, Ray D (2003) Persistent inequality. Rev Econ Stud 70:369–393
Moranfeè F (1998) Savings in chile: what went right?. J Dev Econ 57:201–228
Murphy K, Shleifer K, Vishny A (1989) Indtustrilaization and the big push. J Polit Econ 97:1003–1026
Park D, Rhee C (2005) Saving, growth, and demographic change in korea. J Japan Int Econ 19:394–413
Piketty T (1997) The dynamics of the wealth distribution and the interest rate with credit rationing. Rev Econ Stud 64:173–189
Samwick A (2000) Is pension reform conducive to higher saving?. Rev Econ Stat 82:264–272
Schmidt-Hebbel K, Börsch-Supan A, Miegel M (2001) Chile’s pension revolution coming of age Pension Reform in Six Countries: What Can We Learn from Each Other?. Springer-Verlag, Berlin, pp 139–170
Acknowledgments
We thank Costas Azariadis, Yannis Ioannides, Tatsushi Oka, Kwanho Shin, Enrico Spolaore, Yong Wang for their helpful suggestions and comments as well as Wang Zi for excellent research assistance. The financial support of Singapore Ministry of Education, Academic Research Fund Tier 1 R-122-000-112-112, City University of New York, PSC-CUNY Research Award 60030-40 41, and College of Staten Island Provost’s Research Scholarship Award is gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Alternative specifications
We have assumed a fixed investment size and a linear utility function in our model above. These assumptions reduced the notational burden, made the model analytically tractable and helped to represent ideas by simple graphs and formulas. This section shows that our key results remain robust under a log utility function and as long as there is a minimum investment requirement.
1.1 A.1 Log utility function
One might think that the existence of multiple equilibria depends on the assumption of a linear utility function, which implies an infinitely elastic saving function. This section demonstrates that our results on multiple equilibria and thus the strategic complementarity are robust even when \(u(c)=\log c\).
If s t ≥ 1 − λ, then, from Eqs. 2 and 5, the young agent’s optimal saving is
If s t < 1 − λ, then, from Eqs. 3 and 5, the young agent’s optimal saving must satisfy
imply that the equilibrium pair (w t , s t ) satisfies
where
One can easily verify that s ↦ Γ(s, λ) is a continuous function satisfying boundary conditions Γ(0, λ) = 0, \({\Gamma }(1-\lambda ,\lambda )=\frac {(1+\beta )(1-\lambda )}{\beta }\) and \({\Gamma }(1,\lambda )=\frac {1+\beta }{\beta }\).
Lemma A.1
If \(\lambda <\frac {1}{2+\beta }\), then there exists a unique \(\hat {s} \in (0, 1-\lambda )\) which solves Γ1(s, λ) = 0.
Proof
It follows from Eq. 25that
Onecan easily verify that
Since\(x \mapsto \frac {(1+x)^{2}}{\lambda x^{2}+1-\lambda }\)and\(x\mapsto \frac {\lambda x^{2}-1+\lambda }{\lambda x^{2}+1-\lambda }\)are both increasingfunctions for \(x \in (0,\frac {1-\lambda }{\lambda })\),\({\Gamma }_{1}\left (\frac {x}{1+x},\lambda \right )=0\)admits a unique solution.Since \(x \mapsto \frac {x}{1+x}\)is a monotonictransformation, \({\Gamma }_{1}\left (s,\lambda \right )=0\)also admits at most a unique solution. Since
aunique solution exists if and only if
□
Figure 12a shows the equilibrium pair (w t , s t ) when the utility function is logarithmic and \(\lambda <\frac {1}{2+\beta }\). The figure indicates that there exist multiple equilibria s t for \(w_{t} \in [{\Gamma }(1-\lambda ,\lambda ),{\Gamma }(\hat {s},\lambda )]\).
Proposition A.1
If \(\lambda <\frac {1}{2+\beta }\), then there exists multiple equilibria for \(w(Rs_{t-1}) \in ({\Gamma }(1-\lambda ,\lambda ),{\Gamma }(\hat {s},\lambda ))\) and a unique equilibrium for \(w(Rs_{t-1}) \in (0,{\Gamma }(1-\lambda ,\lambda )) \cup ({\Gamma }(\hat {s},\lambda ),\infty )\).
Proof
The proof of the proposition is a direct consequence of Lemma A.1. If λ (2 + β) < 1, then s ↦ Γ(s, λ) is a non-monotonic function achieving its local maximum at \(s=\hat {s}\) and a local minimum at s = 1 − λ. If λ (2 + β) ≥ 1 then s ↦ Γ(s, λ) is a monotonically increasing function. This impliesthat there exist multiple equilibria if and only if λ (2 + β) < 1 and \(w(Rs_{t-1}) \in ({\Gamma }(1-\lambda ,\lambda ),{\Gamma }(\hat {s},\lambda ))\). Otherwise there always exists a unique equilibrium. □
Let us now compare the linear utility case and the logarithmic utility case. When the utility is logarithmic, then the pair (w t , s t ) solves (24) and (25). Figure 12(b) shows the equilibrium pair (w t , s t ) when the utility function is linear and λ ∈ (ψ 1 (R), ψ 2 (R)).
1.2 A.2 CES production function
This section demonstrates that our results on multiple equilibria and thus the strategic complementarity are robust even when the production function is the following CES function
where α ∈ (0, 1) and σ ∈ (0, ∞) denotes the elasticity of substitution between capital and labor. When σ = 1, we obtain the Cobb-Douglas case.
When the utility function is logarithmic and the production function is CES, then the equilibrium pair (s t−1, s t ) satisfies w(R s t−1) = Γ(s t , λ) where
is the wage function.
Figure 13 plots the the equilibrium pair (s t−1, s t ) satisfying w(R s t−1) = Γ(s t , λ) for different values of σ. The figure shows that multiple equilibria remain a robust phenomenon.
1.3 A.3 The role of minimum investment requirement
We have assumed that the young agents can run at most one project, which required one unit of consumption goods. This section demonstrates that the model remains essentially the same as long as there is a minimum investment requirement. Suppose investment technology is described by
where i t is the investment of the consumption goods, F(i t ) is the produced amount of capital, and I is the minimum investment requirement.
It follows from Eq. 5 that the equilibrium interest rate is
This with Eq. 6 implies that
If I = 0, then \(r_{t+1}=Rf^{\prime }(Rs_{t})\) and the model reduces to a standard OLG model. If I > 0, then, from Eq. 29, we can see that the property of the investment curve H(., λ, R) remains essentially unchanged with respect to s t .
Appendix B: Remaining proofs
Proof of Lemma 3.1
Differentiating both sides of \(H(s,\lambda ,R)=\frac {\lambda \alpha R^{\alpha }s^{\alpha -1}}{1-s}\)with respect to s we obtain that s csolves H s (s, λ, R) = 0 ⇔ \(s^{c}=\frac {1-\alpha }{2-\alpha }\). Since \(\lim _{s \downarrow 0}H(s,\lambda ,R)=\infty \) and \(\lim _{s \uparrow 1}H(s,\lambda ,R)=\infty \), it follows that H (., λ, R)obtains its minimum at s = s c. □
Lemma B.1
The two functions ψ 1 : (0, R +] → [0, 1) and \(\psi _{2}:(0,R^{+}] \to \mathbb R_{++}\) defined in Eq. 10 satisfy
-
(a) ψ 1 is strictly decreasing with \(\lim _{R \downarrow 0}\psi _{1}(R)=1\) and ψ 1 (R +) = 0.
-
(b) ψ 2 is strictly decreasing.
-
(c) ψ 1 and ψ 2 are tangent to each other at R c ∈ (0, R +) and ψ 1 (R) < ψ 2 (R) for any R ≠ R c.
Proof of Lemma B.1
(a) The monotonicity and boundary behavior follow directly from the definition of \(\psi _{1}(R):=1-(\alpha \beta R^{\alpha })^{\frac {1}{1-\alpha }}\) and \(R^{+}:=(\frac {1}{\alpha \beta })^{\frac {1}{\alpha }}\).
(b) The monotonicity and boundary behavior follow directly from the definition of \(\psi _{2}(R):=\frac {1}{\alpha \beta R^{\alpha }}\frac {(1-\alpha )^{1-\alpha }}{(2-\alpha )^{2-\alpha }}\) and \(R^{+}:=(\frac {1}{\alpha \beta })^{\frac {1}{\alpha }}\).
(c) We observe that
if and onlyif 1 − ψ 1 (R)≠s c. Because H(s,⋅, R)is increasing forany given (s, R), thisimplies that ψ 1 (R) < ψ 2(R)if 1 − ψ 1 (R)≠s c, and ψ 1 (R) = ψ 2 (R)if 1 − ψ 1 (R) = s c. Thus solving ψ 1 (R) = ψ 2 (R)is equivalentto solving 1 − ψ 1 (R) = s cor
Since
it follows that ψ 1 and ψ 2 tangenteach other at R = R c. □
Proof of Proposition 3.1
The proposition follows directly from Lemma B.1. □
Proof of Proposition 3.2
The proposition follows directly from Proposition 3.1. □
Lemma B.2
\(\psi _{3}:(0,R^{+}]\to \mathbb R_{++}\) defined in Eq. 14 satisfy
-
(a) ψ 3 is strictly decreasing.
-
(b) ψ 2 and ψ 3 are tangent to each other at R = R cc and ψ 3 (R) < ψ 2 (R) for any R≠R cc.
Proof of Lemma B.2
(a) It directly follows from \(\psi _{3}(R):=\frac {1-\alpha }{\alpha \beta }(1-[(1-\alpha )R^{\alpha }]^{\frac {1}{1-\alpha }})\).
(b) We observe that
if and only if s ∗ ≠ s c. Since H(s,⋅, R) is increasing for any given (s, R), ψ 3 (R) < ψ 2 (R) if s ∗ ≠ s c, and ψ 3 (R) = ψ 2 (R) if s ∗ = s c. Thus, solving ψ 3 (R) = ψ 2 (R)is equivalentto solving s ∗ = s c or
Since \(\psi _{2}^{\prime }(R^{c})=\psi _{3}^{\prime }(R^{c})\), ψ 2 and ψ 3 are tangent toeach other at R = R cc. □
Proof of Proposition 4.1
It can be easily verified that, if \((\beta ,\lambda , R)\in {\mathcal E}\)and either R < R ccor λ < ψ 3 (R),then there exists a unique steady state \(\min \{s_{L},s^{*}\}\). The necessary and sufficient condition for existence of multiple steady states is s M < s ∗.Note that \(\beta <\underline {\beta }(\alpha )\Leftrightarrow s_{H}<s^{*}\). Lemma B.2 establishes that \((\beta ,\lambda , R)\in {\mathcal E}_{1}\) and \((\beta ,\lambda , R)\in {\mathcal E}_{2}\) are necessary and sufficient conditions for s M < s ∗. □
Proof of Lemma 4.1
If \((\beta ,\lambda , R)\in {\mathcal E}_{1}\cup {\mathcal E}_{2}\),then s L < s c < s M < s ∗.If λ is sufficiently close to ψ 2 (R),then s L is sufficiently close to s M , s L ≈ s M .This implies that s L ≈ s c ≈ s M < Ψ(s L ) since s L < s ∗.Hence, s M < Ψ(s L ). Continuity of both s L and s M in parameters ensures the claim. □
Proof
of Proposition 4.3 First, we consider the parameter set\({\mathcal E}_{1}\) corresponding to Proposition 4.1 (b), where \(s_{H}<s^{*}\Leftrightarrow \beta <\underline {\beta }(\alpha )\).As all possible equilibria have positive probability, for any initial condition s 0 ∈ (0, 1),the trajectory will end up in a few iterations in one of the two constants s L or s M and, from that point on, the possible states are only those of the finite set given by Eq.17. The assumption of i.i.d for the stochastic process easily guarantees existence anduniqueness of the stationary distribution. Since the probability of returning to states s L , s M and s H is p L , p M and p H ,respectively, it follows that the stationary probability distribution overall possible states is given by Eq. 18. In this case, the interval [s L , s H ] is a forward invariant set.
Second, we consider the parameter set \({\mathcal E}_{2}\) corresponding to Proposition 4.1 (c), where \(s_{H} \geq s^{*}\Leftrightarrow \beta \geq \underline {\beta }(\alpha )\). For any initial condition s 0 ∈ (0, 1),the trajectory will end up in a few iterations in one of two constants s L or s M and, from that point on, the possible states are only those ofthe countable set given by Eq. 19. It is worthwhile to note that s ∗ does not belong to the above set but belongs toits closure. Since the probability of returning to state s L and s M is p L and p M ,respectively, and both p L and p M are independent of the current state, it follows that the stationary probabilitydistribution over all possible states is given by Eq. 20. In this case, the interval [s L , s ∗)is a forward invariant set. □
Appendix C: Data
Let λ i t = DRate i t /LRate i t where DRate i t and LRate i t are the deposit rate and the lending rate in country i at time t and λ i be the sample average of λ i t . We consider two alternative measures of the saving rate volatility σ i , namely, \(\sqrt {\frac {1}{T}{\sum }_{t=0}^{T}(s_{it}-s_{it-1})^{2}}\) and \(\frac {1}{T}{\sum }_{t=0}^{T}\left | s_{it}-s_{it-1}\right | \) where s i t is the gross saving rate as a percentage of GDP in country i at time t. The data are obtained from the World Bank Development Indicators for the period 1960-2015. First, we calculate the sample average standard deviation of the time series of the saving rate for all 34 OECD countries (Table 1). Second, we calculate the sample average of the deposit to lending rate ratio for 32 countries (Table 2). The deposit rate data are missing for the United States and the lending rate data are missing for Turkey. The deposit rate is measured as the rate at which commercial banks pay on demand, time or savings deposits, while the lending rate is measured as the rate commercial banks charge on loans to prime customers.
The two time series data might not perfectly match for some countries. For example, France has the saving rate from 1975 to 2014 (40 observations) and the lending rate to deposit rate ratio from 1966 to 2004 (39 observations). In this case, 1975-2004 is the overlapping time period (30 observations) and we define the overlap coefficient as 30/40=75%. Among 32 countries, which are included in the sample, the overlap coefficient is 100% for Japan. Table 3 shows that the overlap coefficient is at least 50% for 29 countries, which is 91% of all counties included in the sample.
Rights and permissions
About this article
Cite this article
Kikuchi, T., Vachadze, G. Minimum investment requirement, financial market imperfection and self-fulfilling belief. J Evol Econ 28, 305–332 (2018). https://doi.org/10.1007/s00191-017-0510-z
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00191-017-0510-z
Keywords
- Financial market imperfection
- Strategic complementarity
- Saving rate
- Self-fulfilling belief
- Sunspot
- multiple equilibria