Skip to main content

Rock around the clock: An agent-based model of low- and high-frequency trading

Journal of Evolutionary Economics volume 26, pages 49–76 (2016)Cite this article

Abstract

We build an agent-based model to study how the interplay between low- and high-frequency trading affects asset price dynamics. Our main goal is to investigate whether high-frequency trading exacerbates market volatility and generates flash crashes. In the model, low-frequency agents adopt trading rules based on chronological time and can switch between fundamentalist and chartist strategies. By contrast, high-frequency traders activation is event-driven and depends on price fluctuations. High-frequency traders use directional strategies to exploit market information produced by low-frequency traders. Monte-Carlo simulations reveal that the model replicates the main stylized facts of financial markets. Furthermore, we find that the presence of high-frequency traders increases market volatility and plays a fundamental role in the generation of flash crashes. The emergence of flash crashes is explained by two salient characteristics of high-frequency traders, i.e., their ability to i. generate high bid-ask spreads and ii. synchronize on the sell side of the limit order book. Finally, we find that higher rates of order cancellation by high-frequency traders increase the incidence of flash crashes but reduce their duration.

This is a preview of subscription content, access via your institution.

Access options

Buy single article

Instant access to the full article PDF.

USD 39.95

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Notes

  1. The most famous example of a flash crash occurred on May 6th 2010, when the Dow Jones Industrial Average nosedived by more than 5 % in a few minutes. Financial markets are also characterized by an increasing number of mini flash crashes, a scaled down version of the “May 6th 2010” crash (Golub et al. 2012; Johnson et al. 2012).

  2. Figures vary greatly across studies depending on the market, the definition of HFT considered and the data available. See, for instance, Kirilenko et al. (2011), Aldridge (2013), Gomber and Haferkorn (2013), and SEC (2014).

  3. The uncertainty in the debate about the overall effect of HFT is probably explained by the fact that, so far, no single and concrete definition of HFT prevails (Aldridge 2013; SEC 2014). In addition, the term HFT may apply to a wide variety of trading strategies such as market making, statistical arbitrage, directional trading, electronic liquidity detection (e.g., pinging, sniffing, sniping. See, for instance, Chlistalla et al. 2011; Aldridge 2013; Gomber and Haferkorn 2013; Jones 2013; MacIntosh 2013, and further references therein).

  4. See, for instance, Farmer et al. (2005), Slanina (2008) and Pellizzari and Westerhoff (2009) for detailed studies of the effect of limit-order book models on market dynamics.

  5. See also extensive surveys on HFT in AMF (2010), Chlistalla et al. (2011), Aldridge (2013), Chordia et al. (2013), Gomber and Haferkorn (2013), Jones (2013), and MacIntosh (2013).

  6. As noted by Easley et al. (2012), HFT requires the adoption of algorithmic trading implemented through computers that natively operate on internal event-based clocks. Hence, the study of HFT cannot be reduced to its higher speed only, but it should take into account also the associated new trading paradigm. See also Aloud et al. (2013) for a modeling attempt in the same direction.

  7. For a detailed study of the statistical properties of the limit order book, cf. Bouchaud et al. (2002), Luckock (2003), and Smith et al. (2003).

  8. The price of an executed contract is the average between the matched bid and ask quotes. Note that when both an LF and HF agents send a buy (sell) order with the same price, the order of the LF agent is executed first. The simulation results discussed below do not substantially change when we assume that, in such a limit case, HF agents’ orders have priority over LF traders’ ones. See Appendix 2 for further detail.

  9. The results presented in Section 3 also hold when the market price is defined as the highest or average price of executed transactions in the trading session.

  10. See also Alfarano et al. (2010) for a model with different time horizons.

  11. We assume that N H <N L . The proportion of HF agents vis-à-vis LF ones is in line with empirical evidence (Kirilenko et al. 2011; Paddrik et al. 2011).

  12. On the case for moving away from chronological time in modeling financial series, see Mandelbrot and Taylor (1967), Clark (1973), and Ané and Geman (2000).

  13. In the computation of the mean of the Poisson distribution, the relevant market volumes are weighted by the parameter 0<λ<1.

  14. 14 Simulation exercises in the baseline scenario reveal that the strategies adopted by HF traders are able to generate positive profits, thus justifying their adoption by HF agents in the model. In addition, simulation results indicate that HF traders’ average profits are significantly higher than those of LF traders.

  15. See Windrum et al. (2007) for a discussion of this approach.

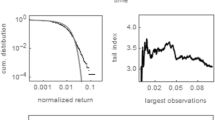
  16. The power-law exponent was estimated using the freely available “power-law package” and based on the procedure developed in Clauset et al. (2009).

  17. Interestingly, our model is also able to generate flash peaks, defined as spikes in asset price of at least 5 % followed by a phase of return to pre-peak price levels of 30 periods at maximum. See, for instance, Johnson et al. (2013) for empirical evidence on the number and duration of flash peaks as well as flash crashes in financial data. The model also reproduces another relevant and recent stylized fact observed during flash crashes, namely the negative correlation between price and volumes (see, e.g., Kirilenko et al. 2011).

  18. See Farmer et al. (2004) for empirical evidence on the relation between liquidity fluctuations and large price changes.

  19. Notice that the concentration of LF orders on the buy side may occur irrespectively of the particular distribution of strategies within this group of agents.

  20. See Haldane (2014) for a discussion of the different proposed explanations of flash crashes.

  21. We also carried out simulations for γ H>20. The above patterns are confirmed. Interestingly, flash crashes completely disappear when the order cancellation rate is very low.

  22. Haldane (2014) also emphasizes that there is a trade-off when deciding whether to impose resting rules (market efficiency versus stability).

  23. Because of space constraints, we do not provide the figures concerning the whole set of stylized facts reproduced by the model. These figures are, however, available from the authors upon request

References

  • Ait-Sahalia Y, Saglam M (2013) High-frequency traders: taking advantage of speed. NBER Working Papers 19531, National Bureau of Economic Research

  • Aldridge I (2013) High-frequency trading: a practical guide to algorithmic strategies and trading systems. Wiley

  • Alfarano S, Lux T, Wagner F (2010) Excess volatility and herding in an artificial financial market: analytical approach and estimation. Paper No. 24719, MPRA

  • Aloud M, Tsang E, Olsen R, Dupuis A (2012) A directional-change event approach for studying financial time series. Economics: The Open-Access, Open-Assessment E-Journa 6:2012–36

    Google Scholar 

  • Aloud M, Tsang E, Olsen R (2013) Modeling the fx market traders’ behavior: an agent-based approach. In: Alexandrova-Kabadjova B, Martinez-Jaramillo S, Garcia-Almanza A, Tsang E (eds) Simulation in computational finance and economics: tools and emerging applications. Hershey PA: Business Science Reference

  • AMF (2010) High frequency trading: the application of advanced trading technology in the european marketplace. Tech. rep., Authority for the Financial Markets (AFM), available at: http://www.afm.nl/layouts/afm/default.aspx/media/files/rapport/2010/hft-report-engels.ashx

  • Ané T, Geman H (2000) Order flow, transaction clock and normality of asset returns. J Finance 55:2259–2284

    Article  Google Scholar 

  • Angel JJ, Harris LE, Spatt CS (2011) Equity trading in the 21st century. The Quart Journ of Fin 1(01):1–53

    Article  Google Scholar 

  • Avellaneda M, Stoikov S (2008) High-frequency trading in a limit order book. Quant Finance 8(3):217–224

    Article  Google Scholar 

  • Baron M, Brogaard J, Kirilenko A (2014) Risk and return in high frequency trading. Working paper, SSRN

  • Bartolozzi M (2010) A multi agent model for the limit order book dynamics. Eur Phys J B 78(2):265–273

    Article  Google Scholar 

  • Bershova N, Rakhlin D (2013) High-frequency trading and long-term investors: a view from the buy-side. J of Inv Strat 2(2):25–69

    Google Scholar 

  • Bouchaud JP, Mézard M, Potters M, et al. (2002) Statistical properties of stock order books: empirical results and models. Quant Finance 2(4):251–256

    Article  Google Scholar 

  • Breckenfelder JH (2013) Competition between high-frequency traders, and market quality. NYU Stern Microstructure Meeting. 2013

  • Brock W, Hommes C (1998) Heterogeneous beliefs and routes to chaos in a simple asset pricing model. J Econ Dynam Control 22(8–9):1235–1274

    Article  Google Scholar 

  • Brogaard J (2010) High frequency trading and its impact on market quality. Northwestern University Kellogg School of Management Working Paper

  • Brogaard J, Hendershott T, Riordan R (2014) High-frequency trading and price discovery. Rev Finan Stud. doi:10.1093/rfs/hhu032

    Google Scholar 

  • Brundsen J (2012) Traders may face nordic-style eu fees for canceled orders. Bloomberg News, 23rd March 2012

  • Carrion A (2013) Very fast money: high-frequency trading on the nasdaq. J Financ Mark 16(4):680–711

    Article  Google Scholar 

  • Cartea Á, Penalva J (2012) Where is the value in high frequency trading? The Quart Journ of Fin 2(03):125004

    Article  Google Scholar 

  • CFTC, SEC (2010) Findings regarding the market events of May 6, 2010. Report of the Staffs of the CFTC and SEC to the Joint Advisory Committee on Emerging Regulatory Issues

  • Chakraborti A, Toke IM, Patriarca M, Abergel F (2011) Econophysics review: I. empirical facts. Quant Finance 11(7):991–1012

    Article  Google Scholar 

  • Chiarella C, He X (2003) Heterogeneous beliefs, risk, and learning in a simple asset-pricing model with a market maker. Macroecon Dyn 7(4):503–536

    Article  Google Scholar 

  • Chlistalla M, Speyer B, Kaiser S, Mayer T (2011) High-frequency trading. Deutsche Bank Research, pp 1–19

  • Chordia T, Goyal A, Lehmann BN, Saar G (2013) High-frequency trading. J Financ Mark 16(4):637–645

    Article  Google Scholar 

  • Clark PK (1973) A subordinated stochastic process model with finite variance for speculative prices. Econometrica 41:135–155

    Article  Google Scholar 

  • Clauset A, Shalizi CR, Newman ME (2009) Power-law distributions in empirical data. SIAM Rev 51(4):661–703

    Article  Google Scholar 

  • Cont R (2001) Empirical properties of asset returns: stylized facts and statistical issues. Quant Finance 1(2):223–236

    Article  Google Scholar 

  • Cont R, Potters M, Bouchaud JP (1997) Scaling in stock market data: stable laws and beyond. Papers arXiv:cond-mat/9705087

  • De Long BJ, Shleifer A, Summers LH, Waldmann RJ (1990) Noise trade risk in financial markets. J Polit Econ 98:703–738

    Article  Google Scholar 

  • Easley D, De Prado ML, O’Hara M (2011) The microstructure of the flash crash: flow toxicity, liquidity crashes and the probability of informed trading. J Portf Manag 37(2):118–128

    Article  Google Scholar 

  • Easley D, López de Prado M, O’Hara M (2012) The volume clock: insights into the high frequency paradigm. J Portf Manag 39(1):19–29

    Article  Google Scholar 

  • Economist T (2012) The fast and the furious. The Economist, 25th February 2012

  • Egginton JF, Van Ness BF, Van Ness RA (2013) Quote stuffing. Available at SSRN 1958281

  • Fama E (1970) Efficient capital markets: a review of theory and empirical work. J Financ 25(2):383–417

    Article  Google Scholar 

  • Farmer JD (2002) Market force, ecology and evolution. Ind Corp Chang 11 (5):895–953

    Article  Google Scholar 

  • Farmer JD, Gillemot L, Lillo F, Szabolcs M, Sen A (2004) What really causes large price changes? Quant Finance 4(4):383–397

    Article  Google Scholar 

  • Farmer JD, Patelli P, Zovko II (2005) The predictive power of zero intelligence in financial markets. PNAS 102(6):2254–2259

    Article  Google Scholar 

  • Franke R, Westerhoff F (2012) Structural stochastic volatility in asset pricing dynamics: estimation and model contest. J Econ Dyn Control 36:1193–1211

    Article  Google Scholar 

  • Golub A, Keane J, Poon SH (2012). High frequency trading and mini flash crashes. Tech. Rep. arXiv:1212.6667

  • Gomber P, Haferkorn M (2013) High-frequency-trading. Business & Information Systems Engineering 5(2):97–99

    Article  Google Scholar 

  • Hagströmer B, Nordén L (2013) The diversity of high-frequency traders. J Financ Mark 16(4):741–770

    Article  Google Scholar 

  • Haldane A (2014) The race to zero. Speech, Bank of England

  • Hanson TA (2011) The effects of high frequency traders in a simulated market. Available at SSRN 1918570

  • Hasbrouck J, Saar G (2009) Technology and liquidity provision: the blurring of traditional definitions. J Financ Mark 12(2):143–172

    Article  Google Scholar 

  • Hasbrouck J, Saar G (2013) Low-latency trading. J Financ Mark 16 (4):646–679

    Article  Google Scholar 

  • Hirschey N (2013) Do high-frequency traders anticipate buying and selling pressure? Available at SSRN 2238516

  • Hoffmann P (2014) A dynamic limit order market with fast and slow traders. J Financ Econ 113(1):156–169

    Article  Google Scholar 

  • Hommes C, Huang H, Wang D (2005) A robust rational route to randomness in a simple asset pricing model. J Econ Dyn Control 29(6):1043–1072

    Article  Google Scholar 

  • Jarrow RA, Protter P (2012) A dysfunctional role of high frequency trading in electronic markets. Int J Theoretical Appl Finance 15(03)

  • Johnson N, Zhao G, Hunsader E, Meng J, Ravindar A, Carran S, Tivnan B (2012) Financial black swans driven by ultrafast machine ecology. Tech. Rep. arXiv:1202.1448

  • Johnson N, Zhao G, Hunsader E, Qi H, Johnson N, Meng J, Tivnan B (2013) Abrupt rise of new machine ecology beyond human response time. Scientific reports 3

  • Jones C (2013) What do we know about high-frequency trading. Research Paper (13–11)

  • Jovanovic B, Menkveld AJ (2012) Middlemen in limit-order markets. Working paper

  • Kirilenko A, Kyle A, Samadi M, Tuzun T (2011) The flash crash: the impact of high frequency trading on an electronic market. Available at SSRN 1686004

  • Kirilenko AA, Lo AW (2013) Moore’s law versus murphy’s law: algorithmic trading and its discontents. The Jour of Ec Persp. pp 51–72

  • Kirman A, Teyssiere G (2002) Microeconomic models for long memory in the volatility of financial time series. Studies in Nonlinear Dynamics & Econometrics 5(4)

  • Lin TC (2012) The new investor. UCLA L Rev 60:678

    Google Scholar 

  • Lo AW, MacKinlay AC (1999) A non-random walk down wall street. Princeton University Press

  • Luckock H (2003) A steady-state model of the continuous double auction. Quant Finance 3(5):385–404

    Article  Google Scholar 

  • Lux T (2006) Financial power laws: Empirical evidence, models, and mechanism. Economics Working Papers 2006,12, Christian-Albrechts-University of Kiel, Department of Economics

  • Lux T, Marchesi M (2000) Volatility clustering in financial markets: a microsimulation of interacting agents. Int J Theoretical Appl Finance 3(4):675–702

    Article  Google Scholar 

  • MacIntosh JG (2013) High frequency traders: angels or devils. CD Howe Institute

  • Madhavan A (2012) Exchange-traded funds, market structure, and the flash crash. Fin Anal J 68(4):20–35

    Article  Google Scholar 

  • Mandelbrot B (1963) The variation of certain speculative prices. J Bus 36 (4):394–419

    Article  Google Scholar 

  • Mandelbrot B, Taylor M (1967) On the distribution of stock price differences. Oper Res 15:1057–162

    Article  Google Scholar 

  • Maslov S (2000) Simple model of a limit order-driven market. Phys A 278 (3):571–578

    Article  Google Scholar 

  • Menkveld AJ (2013) High frequency trading and the new-market makers. Quart J Econ 128(1):249–85

    Article  Google Scholar 

  • Menkveld AJ, Yueshen BZ (2013) Anatomy of the flash crash. Available at SSRN 2243520

  • Paddrik ME, Hayes RL, Todd A, Yang SY, Scherer W, Beling P (2011) An agent based model of the e-mini s&p 500 and the flash crash. Available at SSRN 1932152

  • Pagan A (1996) The econometrics of financial markets. J Empirical Finance 3 (1):15–102

    Article  Google Scholar 

  • Patterson S, Ackerman A (2012) Sec may ticket speeding traders. Wall Street Journal, 23rd February 2012

  • Pellizzari P, Westerhoff F (2009) Some effects of transaction taxes under different microstructures. J Econ Behav Organ 72(3):850–863

    Article  Google Scholar 

  • SEC (2010) Concept release on equity market structure. Release No. 34-61358, 14 January 2010. Available at: http://www.sec.gov/rules/concept/2010/34-61358.pdf

  • SEC (2014) Equity market structure literature review. part ii: high frequency trading. White Paper, 18 March 2014

  • Slanina F (2008) Critical comparison of several order-book models for stock-market fluctuations. Eur Phys J B 61(2):225–240

    Article  Google Scholar 

  • Smith E, Farmer JD, Gillemot L, Krishnamurthy S (2003) Statistical theory of the continuous double auction. Quant Finance 3(6):481–514

    Article  Google Scholar 

  • Sornette D, Von der Becke S (2011) Crashes and high frequency trading. Swiss Finance Institute Research Paper (11–63)

  • Van Kervel V (2014) Market fragmentation and smart order routing technology. Available at SSRN 2021988

  • Wah E, Wellman MP (2013) Latency arbitrage, market fragmentation, and efficiency: a two-market model. In: Proceedings of the 14th ACM conference on electronic commerce. ACM, pp 855–872

  • Westerhoff FH (2008) The use of agent-based financial market models to test the effectiveness of regulatory policies. Jahr Nationaloekon Statist 228(2):195

    Google Scholar 

  • Windrum P, Fagiolo G, Moneta A (2007) Empirical validation of agent-based models: alternatives and prospects. J Artif Soc Soc Simulat 10(2):8

    Google Scholar 

  • Zovko I, Farmer JD (2002) The power of patience: a behavioural regularity in limit-order placement. Quant Finance 2(5):387–392

    Article  Google Scholar 

Download references

Acknowledgments

We are grateful to Sylvain Barde, Francesca Chiaromonte, Jean-Luc Gaffard, Nobi Hanaki, Alan Kirman, Fabrizio Lillo, Frank Westerhoff, and two anonymous referees for stimulating comments and fruitful discussions. We also thank the participants of the Workshop on Heterogeneity and Networks in (Financial) Markets in Marseille, March 2013, of the EMAEE conference in Sophia Antipolis, May 2013, of the WEHIA conference in Reykiavik, June 2013, of the 2013 CEF conference in Vancouver, July 2013 and of the SFC workshop in Limerick, August 2013 where earlier versions of this paper were presented. All usual disclaimers apply. The authors gratefully acknowledge the financial support of the Institute for New Economic Thinking (INET) grants #220, “The Evolutionary Paths Toward the Financial Abyss and the Endogenous Spread of Financial Shocks into the Real Economy”.

Author information

Authors and Affiliations

  1. CEREFIGE - ICN Business School, 13 Rue Michel Ney, 54000, Nancy, France

    Sandrine Jacob Leal

  2. OFCE, SKEMA Business School, 60 Rue Dostoïevski, 06902, Sophia Antipolis Cedex, France

    Mauro Napoletano

  3. Istituto di Economia Scuola Superiore Sant’Anna, Piazza Martiri della Libertá 33, 56127, Pisa, Italy

    Mauro Napoletano, Andrea Roventini & Giorgio Fagiolo

  4. OFCE, Sophia-Antipolis, France

    Andrea Roventini

Authors
  1. Sandrine Jacob Leal
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mauro Napoletano
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Andrea Roventini
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Giorgio Fagiolo
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Sandrine Jacob Leal.

Appendices

Appendix 1: Parameters

Table 4 Parameters values in the baseline scenario
Full size table

Appendix 2: Model results under alternative time-order priority

In the paper, we assume that HF orders are inserted in the book after LF ones and before the actual matching takes place. As discussed in Section 2.1, this allows us to account for the low-latency feature of high-frequency trading strategies. Accordingly, when both an LF and HF agents send a buy (sell) order with the same price, the order of the LF agent is executed first (see footnote 8). In order to check the sensitivity of our results to the latter assumption, we have also performed simulations assuming that time priority was instead given to HF orders. The results of these simulations show first that all the properties of the model are robust to this alternative assumption. For instance, Fig. 11 shows that zero-autocorrelation of returns is reproduced by the model also in this alternative scenario. The same holds for the presence of volatility clustering (see Fig. 12).Footnote 23 Finally, Tables 5 and 6 report, respectively, the results on market statistics and agents’ order aggressiveness. The figures in both tables confirm, as explained in footnote 8, that these model’s results do not substantially change when we assume that where two orders have the same price, HF agents’ orders have priority over LF traders’ ones.

Fig. 11
figure 11

Baseline scenario with time-order priority given to HF orders. Price-returns sample autocorrelation function (solid line) together with 95 % confidence bands (dashed lines). Values are averages across 50 independent Monte-Carlo runs

Full size image
Fig. 12
figure 12

Baseline scenario with time-order priority given to HF orders. Sample autocorrelation functions of absolute price returns (solid line) together 95 % confidence bands (dashed lines). Values are averages across 50 independent Monte-Carlo runs

Full size image
Table 5 Market statistics for baseline scenario with time-order priority given to HF orders
Full size table
Table 6 Orders’ aggressiveness ratios for different categories of traders and different market phases
Full size table

Rights and permissions

Reprints and Permissions

About this article

Verify currency and authenticity via CrossMark

Cite this article

Jacob Leal, S., Napoletano, M., Roventini, A. et al. Rock around the clock: An agent-based model of low- and high-frequency trading. J Evol Econ 26, 49–76 (2016). https://doi.org/10.1007/s00191-015-0418-4

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00191-015-0418-4

Keywords

  • Agent-based models
  • Limit order book
  • High-frequency trading
  • Low-frequency trading
  • Flash crashes
  • Market volatility

JEL Classification

  • G12
  • G01
  • G14
  • C63