Modeling the gravitational field by using CFD techniques

Abstract

A harmonic scalar field has a Laplacian (i.e., both source-free and curl-free) gradient vector field and vice versa. Despite the good performance of spherical harmonic series on modeling the gravitational field generated by spheroidal bodies (e.g., the Earth), the series may diverge inside the Brillouin sphere enclosing all field-generating mass. Divergence may realistically occur when determining the gravitational fields of asteroids or comets that have complex shapes, which is known as the complex-boundary value problem (CBVP). To overcome this weakness, we propose a new spatial-domain numerical method based on the equivalence transformation which is well known in the fluid dynamics community: a potential-flow velocity field and a gravitational force vector field are equivalent in a mathematical sense, both referring to a Laplacian vector field. The new method abandons the perturbation theory based on the Laplace equation, and, instead, derives the governing equation and the boundary condition of the potential flow from the conservation laws of mass, momentum and energy. Correspondingly, computational fluid dynamics (CFD) techniques are introduced as a numerical solving scheme. We apply this novel approach to the gravitational field of the comet 67P/Churyumov–Gerasimenko which has an irregular shape. The method is validated in a closed-loop simulation by comparing the result with a direct integration of Newton’s formula. Both methods are consistent with a relative magnitude discrepancy at the percentage level and with a small directional difference root-mean-square value of $0.78^{\circ }$. Moreover, the Laplacian property of the potential flow’s velocity field is proved mathematically. From both theoretical and practical points of view, the new numerical method is able to overcome the divergence problem and, hence, has a good potential for solving CBVPs.

1 Introduction

A gravitational field is the influence that a mass body extends into the space around itself, producing a force on another mass body (Feynman et al. 2011). The external gravitational field is curl-free, i.e., it is conservative, and it is divergence-free, i.e., it has no sources or sinks. The main objective of physical geodesy is to establish a gravitational model, on the Earth’s surface and in outer space, to the extent made possible by existing data, mathematical analytical tools and numerical computational tools (Sansò et al. 2012).

Fig. 1

Mass distributions with increasing complexity. a Mass point; b mass ball with homogeneous density; c mass ball with inhomogeneous density; d spheroidal mass body; e and f irregular shaped mass bodies. Red dashed spheres denote Brillouin spheres, i.e., the minimum spheres encompassing the mass bodies

By far, the external gravitational field modeling methods, in terms of boundary value problem solutions, can be classified into two categories: analytical ones and numerical ones.

The analytical methods mainly refer to harmonic series expansions in different coordinate systems, e.g., spherical harmonic series (e.g., Heiskanen and Moritz 1967; Sneeuw 1994; Sansò and Sideris 2013 and references therein), spheroidal harmonic series (e.g., Jekeli 1988; Thong and Grafarend 1989; Fukushima 2014), ellipsoidal harmonic series (e.g., Garmier and Barriot 2001; Garmier et al. 2002; Hu and Jekeli 2015; Park et al. 2014), rectangular harmonic series (Alldredge 1981, 1982) and bispherical harmonic series (Andert et al. 2015). Among them, spherical harmonic series are the common tool of choice for building advanced geopotential models. For example, the Earth Gravitational Model 2008 (EGM2008; Pavlis et al. 2012) is such a potential model developed from a comprehensive set of terrestrial measurements, satellite altimetry, airborne gravimetry and topographic data. Spherical harmonics are widely used in Earth gravitational field modeling due to the consistency between the shapes of the coordinate sphere and the Earth. In general, applications of harmonic series depend on the shape of a mass body, aiming at narrowing possible divergence regions, i.e., the free space between the mass surface and the Brillouin surface (i.e., sphere, spheroid or ellipsoid enclosing the field-generating mass in cases of corresponding coordinates; Hu and Jekeli 2015). For example, the convergence of spherical harmonics is guaranteed outside Brillouin sphere. However, when it comes to irregularly shaped mass bodies such as asteroids or comets, the series at points near the surface of the body might diverge due to the discrepancy between the shape of the body and the Brillouin sphere (Fig. 1d, e, f). This indicates that spherical harmonics are adequate for representing gravitational fields of sphere-like bodies, rather than those of irregular shaped bodies (Reimond and Baur 2016). Recently, the divergence behavior of harmonic series expansions of gravitational field functionals has been intensively studied for irregularly shaped bodies (e.g., Takahashi et al. 2013; Takahashi and Scheeres 2014; Hu and Jekeli 2015; Hirt and Kuhn 2018). These studies reveal a great challenge to completely overcome the divergence of analytical series, because for most cases a realistic mass surface seldom coincides with its corresponding Brillouin surface. This open problem can be briefly summarized as the modeling of gravitational fields generated by irregularly shaped bodies (corresponding to the cases in Fig. 1e, f). In this study, it is denoted as complex-boundary value problem (CBVP), which has not been well solved so far compared to other boundary value problems, e.g., those solvable by Newton’s formula (Fig. 1a, b), Stokes’s integral (Fig. 1c) and Molodensky’s series (Fig. 1d).

Complementary to analytical methods, numerical approaches are characterized by the powerful capacity of solving nonlinear problems. They subdivide a large problem into smaller and simpler parts (i.e., it is a way of linearization), each one corresponding to a set of linear algebraic equations. This advantage makes numerical schemes widely used in solving nonlinear problems, and consequently, they play important roles in different fields. For example, the finite element method is able to analyze strain/stress distributions of highly complex engineering structures, which is usually impossible for analytical solutions. Similarly, geodetic researchers appeal to numerical schemes for solving the CBVPs, in view of the high-degree nonlinearity of gravitational fields with complex mass distributions. However, this has not been realized up to now, despite various attempts applying various numerical methods, e.g., the finite element method (FEM; Meissl 1981; Bian and Chao 1991; Fašková et al. 2010), the boundary element method (BEM; Klees 1995; Lehmann and Klees 1999; Čunderlík et al. 2008) and the finite volume method (FVM; Macák et al. 2012, 2015; Medl’a et al. 2018).

Historically, the state of the art of gravitational field determination seems to experience a bottleneck, blocked by the CBVP. The tremendous efforts on addressing this open problem versus the somewhat unsatisfactory advancement implies a possible lack of information within the scope of geodesy on solving this problem, which may need to draw on knowledge from other research fields. Computational fluid dynamics (CFD) offers such a chance. CFD is the analysis of systems involving fluid flow, heat transfer and associated phenomena by means of computer-based simulation (Versteeg and Malalasekera 1995). Benefiting from the increasing computer power, CFD techniques developed rapidly in the past decades. The fundamental basis of almost all CFD problems is the Navier–Stokes equations defining single-phase (gas or liquid) fluid flows. Imposed with specific constraints (e.g., setting parameters or removing terms), the fundamental equations of a general flow can be simplified to formulate various fluid flows, among which the potential flow is an idealized one that occurs in the case of incompressible, inviscid and irrotational fluid particles. In particular, the velocity field of potential flow is Laplacian, i.e., source-free and curl-free.

The above analysis shows that the gravitational vector field and the potential flow velocity field are equivalent in the sense that both are Laplacian vector fields. For this reason, we propose to utilize potential flow theory as well as the CFD technique to model gravitational fields, especially the CBVPs. The governing equation of the potential flow is adopted as an alternative to the Laplace equation when modeling the gravitational field.

This paper has two objectives: (1) to illustrate the principle and workflow of the new gravitational field modeling method; (2) to give a proof-of-concept by applying the new method to the very irregularly shaped comet 67P/Churyumov–Gerasimenko (hereafter referred to as comet 67P). The two parts are arranged in Sects. 2 and 3, respectively. In Sect. 2, first, the principle of the equivalence transformation is outlined (Sect. 2.1), involving the issues of the three-dimensional potential flow, the CFD techniques and the pipe transformation; then, the three issues are addressed in Sect. 2.2–2.4, respectively. In Sect. 3, a computational workflow is devised to model the gravitational field of the comet 67P and the result is validated in a closed-loop simulation. The advantages and potential applications of the new method are discussed in Sect. 4, and a conclusion is given in Sect. 5.

2 Methodology

2.1 Equivalence transformation

The main idea of our method is based on the equivalence transformation between the gravitational vector field and the potential flow velocity field. Table 1 compares the two physical objects regarding their common and different points. Although belonging to different research areas, both vector fields are Laplacian and thereby mutually equivalent. The gravitational potential, the gravitational vector and the plumb line correspond to the potential flow velocity potential, the potential flow velocity vector and the stream line, respectively. The gravitational vector ${\varvec{g}}$ and the potential flow velocity vector ${\varvec{v}}$ are interchangeable when formulating either vector field. For example, the governing equations and boundary condition of the potential flow can be used for the gravitational field modeling, with the velocity ${\varvec{v}}$ replaced by the gravitational vector ${\varvec{g}}$. In Sects.  2.2–2.4, we first derive the mathematical expressions (i.e., the governing equations and the boundary condition) of the potential flow, then introduce the principle of the CFD techniques exemplified with a pipe flow, and then transform the potential-flow pipe to make it suitable for gravitational field modeling. Finally, after substituting the velocity term ${\varvec{v}}$ with the gravitational term ${\varvec{g}}$ in the derived equations, the framework of our new method is established.

Table 1 Equivalence and difference between the gravitational vector field and the potential flow velocity field

2.2 Three-dimensional potential flow

Potential flow is an idealized flow of steady, irrotational, inviscid and incompressible fluid particles. The velocity field of the potential flow is Laplacian for two reasons. On the one hand, there is no loss or gain of either mass or kinetic energy for the entire flow system, making the velocity field source-free. On the other hand, the smooth interfaces between fluid particles make the particles torque-free and thereby the velocity field curl-free. In the following content, we first give the mathematical description of the three-dimensional Newtonian flow and then impose it with the constraints listed in Table 2, to build the fundamental equations of the potential flow.

2.2.1 Governing equation

The governing equations of Newtonian flow include:

• Continuity equation:

  $$\begin{aligned} \frac{\partial \rho }{\partial t}+\nabla \cdot \left( \rho \varvec{v} \right) =0 \end{aligned}$$

  (1)

• Momentum equations (Navier–Stokes equations):

  $$\begin{aligned} \frac{\partial \left( \rho \varvec{v} \right) }{\partial t}+\nabla \cdot \left( \rho \varvec{v} \otimes \varvec{v} \right) =\nabla \cdot \varvec{\tau } +\varvec{B}-\nabla p \end{aligned}$$

  (2)

where $\varvec{\tau }$ is the stress tensor

$$\begin{aligned} \varvec{\tau } = \mu \left( {\nabla \varvec{v} + {{\left( {\nabla \varvec{v}} \right) }^T}} \right) + \lambda \left( {\nabla \cdot \varvec{v}} \right) \varvec{I} \end{aligned}$$

(3)

Equations (1) and (2), respectively, state the conservation laws of mass and momentum under Eulerian description. The variables involved in the two equations are functions of space and time: $\varvec{v}$ denotes the velocity vector comprising three components ${v_1}$, ${v_2}$ and ${v_3}$; $\rho$ is density; p is pressure; the dynamic viscosity $\mu$ and the bulk viscosity $\lambda$ are the Lamé parameters which control the flow behavior due to friction; $\varvec{B}$ is a body force (e.g., gravitation, Coriolis force or electromagnetic force). Among these variables, the three velocity components ${v_1}$, ${v_2}$ and ${v_3}$ and the pressure p are the unknowns to solve for (see the SIMPLE algorithm in Sect. 2.3.2). In Eq. (2), the operator $\otimes$ denotes the outer product, and the outer product of two vectors $\varvec{u}$ and $\varvec{v}$ is a matrix $\varvec{w}$ given by ${{w_{ij}} = {u_i}{u_j}}$. With this definition, the second term on the left hand side of Eq. (2) can be expanded as follows:

$$\begin{aligned} \nabla \cdot \left( \rho \varvec{v}\otimes \varvec{v} \right) =\rho \left( \nabla \cdot \varvec{v} \right) \varvec{v}+\rho \varvec{v}\cdot \nabla \varvec{v} \end{aligned}$$

(4)

Inserting the above term into Eq. (2), one obtains

$$\begin{aligned} \frac{{\partial \left( {\rho {\varvec{v}}} \right) }}{{\partial t}} + \rho \left( {\nabla \cdot {\varvec{v}}} \right) {\varvec{v}} + \rho {\varvec{v}} \cdot \nabla {\varvec{v}} = \nabla \cdot \varvec{\tau } + {\varvec{B}} - \nabla p \end{aligned}$$

(5)

Then, applying the first two constraints listed in Table 2 (i.e., $\rho =1.0\,\mathrm {kg/m^3}$ and $\frac{\partial }{{\partial t}}\left( \cdot \right) = 0$), Eqs. (1) and (5), respectively, transform into

$$\begin{aligned} \nabla \cdot \varvec{v}=0 \end{aligned}$$

(6)

Table 2 Constraints imposed on Newtonian flow and the corresponding functions

and

$$\begin{aligned} {\varvec{v}} \cdot \nabla {\varvec{v}} = \nabla \cdot \varvec{\tau } + {\varvec{B}} - \nabla p \end{aligned}$$

(7)

Note that, on account of Eq. (6), the second term of the left hand side of Eq. (5), $\rho \left( {\nabla \cdot {\varvec{v}}} \right) {\varvec{v}}$, does not exist in Eq. (7) anymore. Further, imposing on Eq. (7) as well as Eq. (3) the other two constraints given in Table 2 (i.e., $\mu =\lambda =0\,\mathrm {Pa \cdot s}$ and $\varvec{B} = \varvec{0}$) yields

$$\begin{aligned} \varvec{v}\cdot \nabla \varvec{v}=-\nabla p \end{aligned}$$

(8)

Taken together, the combination of Eqs. (6) and (8) serve as the governing equations of the three-dimensional potential flow as follows:

$$\begin{aligned} \left\{ \begin{matrix} \nabla \cdot \varvec{v}=0 \\ \varvec{v}\cdot \nabla \varvec{v}=-\nabla p \\ \end{matrix} \right. \end{aligned}$$

(9)

2.2.2 Boundary condition

The Bernoulli equation is a statement of the conservation of energy for an inviscid flow, which implies an increase in the speed of a fluid simultaneously with a decrease in pressure. The Bernoulli equation for unsteady inviscid flows has the following form:

$$\begin{aligned} -\frac{\partial \phi }{\partial t}+\frac{{{v}^{2}}}{2}+\frac{p}{\rho }+ \Psi =C \end{aligned}$$

(10)

where $\phi$ is the velocity potential, C is a constant number, and $\Psi$ is the conservative body force potential defined as $\nabla \Psi = \varvec{B}$. Because the body force is not considered in this study (i.e., $\varvec{B}=\varvec{0}$), the body force potential is a constant as well (i.e., $\Psi =const.$). Applying the constraints given in Table 2, Eq. (10) transforms into the following formula:

$$\begin{aligned} p=-\frac{1}{2}{{v}^{2}} \end{aligned}$$

(11)

which holds throughout the potential flow and is particularly used for calculating the boundary condition in our method. Note that the constants involved in Eq. (10) have been set to zero, i.e., $\Psi =C=0$, and such treatment has no influence on the final solution in a vector form.

2.3 CFD techniques

CFD is an interdisciplinary research field involving numerical analysis, fluid mechanics and computer science. As shown in Fig. 2, it mainly includes four modules: problem identification, preprocessing, solving and post-processing. The goal of the first step is to analyze the feasibility of the three subsequent steps. In CFD the finite volume method is a method for representing and evaluating partial differential equations in the form of algebraic equations (LeVeque 2002; Toro 1999). This section mainly focuses on the basic steps of the finite volume method, illustrated with a three-dimensional pipe flow (see Fig. 3a). On account of brevity and clarity, the control volumes for the illustration purpose are hexahedrons.

Fig. 2

Workflow of the CFD techniques

Fig. 3

Illustration of the finite volume method. a Discretization of a pipe flow domain. b Notations of a finite control volume

2.3.1 Step 1: Grid generation

The first step in the finite volume method is to divide the computation domain into discrete control volumes (a.k.a. cells, elements) where the variable of interest (i.e., velocities and pressure) is located at the nodal point (i.e., the centroid of the control volume). Assume that a number of nodal points are located inside the domain, that the faces of control volumes are positioned mid-way between adjacent nodes, and that each node is surrounded by a control volume.

A system of notation is established as follows. Figure 3b shows a general nodal point identified by P with six neighboring nodes in a three-dimensional geometry identified as west, east, south, north, bottom and top nodes (W, E, S, N, B, T). The lowercase notation, w, e, s, n, b and t is used to refer to cell faces in the corresponding directions. The ${x_1}$-, ${x_2}$- and ${x_3}$-components of the coordinate system are aligned with the directions of WE, SN and BT, respectively. The distances between two geometrical elements are denoted as $\delta x_1^{ \square \square }$, $\delta x_2^{ \square \square }$ and $\delta x_3^{ \square \square }$, with the superscripts $\square \square$ occupied by the node or face notations. For example, the distances between the nodes P and T, between the node P and the face t and between the faces b and t, are identified by $\delta x_3^{PT}$, $\delta x_3^{Pt}$ and $\delta x_3^{bt}$, respectively. By contrast, the area A of a given face t can be denoted as ${A^t}$.

2.3.2 Step 2: Discretization

A critical operation of the finite volume method is the integration of the governing equation set (9) over a control volume to yield a discretized equation at its nodal point P. For the control volume defined in Fig. 3b, this gives

$$\begin{aligned} \left\{ \begin{array}{lc} \int \limits _{\Delta V}{\nabla \cdot \varvec{v}\mathrm{d}V}=0\text { } &{} {} \\ \int \limits _{\Delta V}{\nabla \cdot \left( \varvec{v}{{v}_{i}} \right) \mathrm{d}V}=\int \limits _{\Delta V}{\left( -\frac{\partial p}{\partial {{x}_{i}}} \right) \mathrm{d}V,} &{} (i=1,2,3) \\ \end{array} \right. \end{aligned}$$

(12)

where $\Delta V$ is the integral volume of each cell. Note that the integrand in the above second equation, $\nabla \cdot \left( {{\varvec{v}}{v_i}} \right)$, is equal to the left hand side of the potential flow’s momentum equation (i.e., the second constituent of equation set (9)), ${\varvec{v}} \cdot \nabla {\varvec{v}}$, by jointly considering the identity, $\nabla \cdot \left( {{\varvec{v}}{v_i}} \right) = {\varvec{v}} \cdot \nabla {v_i} + \left( {\nabla \cdot {\varvec{v}}} \right) {v_i}$, and the potential flow’s continuity equation (i.e., the first constituent of equation set (9)), $\nabla \cdot {\varvec{v}} = 0$. The equation set (12) represents the flux balances of the mass and the momentum for potential flows through a control volume. The left hand side gives the net convective flux of the property (mass or momentum), and the right hand side contains the generation or destruction of the corresponding property within the control volume.

Applying Gauss’ theorem to the left hand side terms of equation set (12), one can obtain

$$\begin{aligned} \left\{ \begin{array}{lc} \int \limits _{A}{\varvec{n}\cdot \varvec{v}\mathrm{d}A}=0\text { } &{} {} \\ \int \limits _{A}{\varvec{n}\cdot \left( \varvec{v}{{v}_{i}} \right) \mathrm{d}A}=\int \limits _{\Delta V}{\left( -\frac{\partial p}{\partial {{x}_{i}}} \right) \mathrm{d}{{x}_{1}}\mathrm{d}{{x}_{2}}\mathrm{d}{{x}_{3}}}, &{} (i=1,2,3) \\ \end{array}\right. \end{aligned}$$

(13)

where $\varvec{n}$ is the unit normal vector of the control volume face element dA, and the terms relating to the volume integration are defined as follows:

$$\begin{aligned} \left\{ {\begin{array}{*{20}{c}} {A_1^P = d{x_2}d{x_3}},&{}{\Delta p_1^P = {p^e} - {p^w}}\\ {A_2^P = d{x_1}d{x_3}},&{}{\Delta p_2^P = {p^n} - {p^s}}\\ {A_3^P = d{x_1}d{x_2}},&{}{\Delta p_3^P = {p^t} - {p^b}} \end{array}} \right. \qquad \end{aligned}$$

(14)

Expanding equation set (13) with the help of Eq. (14) yields

$$\begin{aligned} \left( {{A^e}v_1^e - {A^w}v_1^w} \right) + \left( {{A^n}v_2^n - {A^s}v_2^s} \right) + \left( {{A^t}v_3^t - {A^b}v_3^b} \right) = 0 \nonumber \\ \end{aligned}$$

(15)

and

$$\begin{aligned} \begin{array}{l} \left( {{A^e}v_1^ev_i^e - {A^w}v_1^wv_i^w} \right) + \left( {{A^n}v_2^nv_i^n - {A^s}v_2^sv_i^s} \right) \\ + \left( {{A^t}v_3^tv_i^t - {A^b}v_3^bv_i^b} \right) = - A_i^P\Delta p_i^P\mathrm{{ , }}\left( {i = 1,2,3} \right) \end{array} \end{aligned}$$

(16)

Note that in Eq. (16) the unknowns of velocity components with lowercase superscripts are defined at the control volume faces, rather than at the nodal points where the final solution should be defined. Therefore, the velocity components at the control volume faces must be expressed by those at the nodal points with a specific interpolation scheme. Taking the central differencing scheme for example, the interpolated values at the faces are given by

$$\begin{aligned} \left\{ \begin{array}{ccc} v_{i}^{w}=\frac{1}{2}\left( v_{i}^{W}+v_{i}^{P} \right) ,\text { }v_{i}^{e}=\frac{1}{2}\left( v_{i}^{P}+v_{i}^{E} \right) \\ v_{i}^{s}=\frac{1}{2}\left( v_{i}^{S}+v_{i}^{P} \right) ,\text { }v_{i}^{n}=\frac{1}{2}\left( v_{i}^{P}+v_{i}^{N} \right) &{} , &{} \left( i=1,2,3 \right) \\ v_{i}^{b}=\frac{1}{2}\left( v_{i}^{B}+v_{i}^{P} \right) ,\text { }v_{i}^{t}=\frac{1}{2}\left( v_{i}^{P}+v_{i}^{T} \right) \\ \end{array} \right. \nonumber \\ \end{aligned}$$

(17)

Inserting Eq. (17) into Eq. (16) followed by reorganization yields the linear form that is solvable by matrix inversion:

$$\begin{aligned}&{{a}^{P}}v_{i}^{P}-{{a}^{W}}v_{i}^{W}-{{a}^{E}}v_{i}^{E}-{{a}^{S}}v_{i}^{S} -{{a}^{N}}v_{i}^{N}-{{a}^{B}}v_{i}^{B}-{{a}^{T}}v_{i}^{T}\nonumber \\&\qquad =-A_{i}^{P}\Delta p_{i}^{P}\text { , }\left( i=1,2,3 \right) \end{aligned}$$

(18)

where

$$\begin{aligned} \left\{ \begin{aligned}&\begin{matrix} {{a}^{W}}=\frac{1}{2}{{A}^{w}}{{{v}}^{w}_{1}}, &{}\quad {{a}^{E}}=-\frac{1}{2} {{A}^{e}}{{{v}}^{e}_{1}} \\ \end{matrix} \\&\begin{matrix} {{a}^{S}}=\frac{1}{2}{{A}^{s}}{{{v}}^{s}_{2}}, &{}\quad {{a}^{N}} =-\frac{1}{2}{{A}^{n}}{{{v}}^{n}_{2}} \\ \end{matrix} \\&\begin{matrix} {{a}^{B}}=\frac{1}{2}{{A}^{b}}{{{v}}^{b}_{3}}, &{}\quad {{a}^{T}} =-\frac{1}{2}{{A}^{t}}{{{v}}^{t}_{3}} \\ \end{matrix} \\&{{a}^{P}}=-\left( {{a}^{W}}+{{a}^{E}}+{{a}^{S}}+{{a}^{N}}+{{a}^{B}} +{{a}^{T}} \right) \\ \end{aligned} \right. \end{aligned}$$

(19)

Note that for different interpolation schemes the form of Eq. (19) varies. Since the coefficients of the linear equation (18) still contain the unknown variables (i.e., velocities; refer to Eq. (19)), an iterative algorithm is needed to solve this equation system, which is the main topic of Sect. 2.3.3.

2.3.3 Step 3: Solution of equations

The aim of the finite volume method is to solve for the velocities and the pressure based on the discretized governing equations (15) and (18). Specifically, the discretized equation (18) must be set up at each nodal point in the flow domain; for the nodal points adjacent to the domain boundaries, boundary conditions can be incorporated. After constituting the discretized momentum equations (18) for all the control volumes, one can solve for the velocities $v_i^P\left( {i = 1,2,3} \right)$ and the pressure p at the nodal points. At the same time, the continuity equation (15) needs to be satisfied as well.

However, the algebraic equation system (15) and (18) is not easy to solve due to the following two reasons:

• (1) The momentum equations contain nonlinear quantities. For example, the coefficients of the momentum equations, Eq. (19), involve the velocities on cell faces, which, however, are quantities estimated from the unknowns.

• (2) There is no transport equation for the pressure which is also one unknown variable in the flow problem. The pressure is coupled with the velocities in the momentum equations (18) while not in the continuity equation (15).

In CFD, the SIMPLE algorithm developed by Patankar and Spalding (1972) is a widely used numerical method of solving the Navier–Stokes equations. SIMPLE is an acronym for semi-implicit method for pressure linked equations. It is essentially based on a guess-and-correct procedure. Figure 4 shows the basic steps of the SIMPLE algorithm. The principle is introduced as follows.

Fig. 4

Workflow of the SIMPLE algorithm

Starting with the rewritten form of the momentum equations (18) as follows:

$$\begin{aligned} {{a}^{P}}v_{i}^{P*}-\sum {{{a}^{nb}}v_{i}^{nb*}}=-A_{i}^{P}\Delta p_{i}^{P*}, \left( i=1,2,3 \right) \end{aligned}$$

(20)

where the superscript * marks the guessed quantities and the superscript nb denotes the neighboring nodes of the node P, e.g., those marked by E, W, N, S, B, and T, in Fig. 3b. The coefficients of Eq. (20), depending on the interpolation type, can be calculated with the guessed quantities and with formulae similar to equation set (19). For the pressure field and the velocity field, the differences between the corrected and the guessed quantities are, respectively, defined as

$$\begin{aligned} \delta p=p-{{p}^{*}} \end{aligned}$$

(21)

and

$$\begin{aligned} \delta {{v}_{i}}={{v}_{i}}-v_{i}^{*}, \left( i=1,2,3 \right) \end{aligned}$$

(22)

Due to the linearity, the pressure and the velocity terms in Eq. (20) can be substituted, respectively, with their corrections, yielding

$$\begin{aligned} {{a}^{P}}\delta v_{i}^{P}-\sum {{{a}^{nb}}\delta v_{i}^{nb}}=-A_{i}^{P}\Delta \left( \delta p_{i}^{P} \right) ,\quad \left( i=1,2,3 \right) \nonumber \\ \end{aligned}$$

(23)

in which the coefficient matrix of the velocities is diagonal dominant. In order to improve the computational efficiency, the non-diagonal terms are omitted, which is the main approximation of the SIMPLE algorithm (Versteeg and Malalasekera 1995). Then, one obtains

$$\begin{aligned} \delta v_{i}^{P}=d_{i}^{P}\Delta \left( \delta p_{i}^{P} \right) , \left( i=1,2,3 \right) \end{aligned}$$

(24)

where

$$\begin{aligned} d_{i}^{P}=-\frac{A_{i}^{P}}{a_{i}^{P}} \end{aligned}$$

(25)

Inserting Eq. (24) into Eq. (22) and rearranging gives the corrected velocities:

$$\begin{aligned} {{v}_{i}}=v_{i}^{*}\text {+}\delta {{v}_{i}}, \left( i=1,2,3 \right) \end{aligned}$$

(26)

In order to ensure the continuity of the solution, the continuity equation is incorporated by inserting Eq. (26) into Eq. (15), together taking into consideration Eqs. (14) and (24). This generates

$$\begin{aligned}&{{a}^{P}}\delta {{p}^{P}}-{{a}^{E}}\delta {{p}^{E}}-{{a}^{W}}\delta {{p}^{W}} -{{a}^{N}}\delta {{p}^{N}}-{{a}^{S}}\delta {{p}^{S}}\nonumber \\&\quad -{{a}^{T}}\delta {{p}^{T}}-{{a}^{B}}\delta {{p}^{B}}=\delta {{b}^{P}} \end{aligned}$$

(27)

where

$$\begin{aligned} \left\{ \begin{aligned}&\begin{matrix} {{a}^{E}}={{\left( Ad \right) }^{e}}, &{}\quad {{a}^{W}}={{\left( Ad \right) }^{w}} \\ \end{matrix} \\&\begin{matrix} {{a}^{N}}={{\left( Ad \right) }^{n}}, &{}\quad {{a}^{S}}={{\left( Ad \right) }^{s}} \\ \end{matrix} \\&\begin{matrix} {{a}^{T}}={{\left( Ad \right) }^{t}}, &{}\quad {{a}^{B}}={{\left( Ad \right) }^{b}} \\ \end{matrix} \\&{{a}^{P}}={{a}^{E}}+{{a}^{W}}+{{a}^{N}}+{{a}^{S}}+{{a}^{T}}+{{a}^{B}} \\&\delta {{b}^{P}}={{\left( {{v}^{*}}A \right) }^{w}}-{{\left( {{v}^{*}}A \right) }^{e}}\\&\quad +{{\left( {{v}^{*}}A \right) }^{s}}-{{\left( {{v}^{*}}A \right) }^{n}} +{{\left( {{v}^{*}}A \right) }^{b}}-{{\left( {{v}^{*}}A \right) }^{t}} \\ \end{aligned} \right. \qquad . \end{aligned}$$

(28)

Once the pressure corrections at all nodes are obtained by solving the linear equations (27) built for all control volumes, the corrected pressure can be calculated by

$$\begin{aligned} p={{p}^{*}}\text {+}\delta p \end{aligned}$$

(29)

After that, with the corrected velocities from Eq. (26) and the corrected pressure from Eq. (29), the algorithm is able to enter into the next step: either the next iteration or termination, as shown in Fig. 4. The SIMPLE algorithm does not stop until the balances of mass and the momentums of the three velocity components are satisfied.

Fig. 5

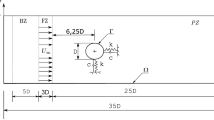
Geometrical transformation of a pipe containing potential flows. a and g are the initial and end shapes, respectively. The potential flow velocities in g are equivalent to the gravitational vector field of a mass body whose surface is the outlet. In g, the center of the outer sphere (i.e., the inlet) is identical with the center of the mass, and the scalar gravitation on the outer sphere is calculated with a point mass assumption, in which the mass is condensed at the center as a mass point, when the radius is large enough, e.g., ten times the average size of the mass body in this study

Fig. 6

Shape model of the comet 67P/Churyumov–Gerasimenko

2.4 Pipe transformation

Up to this point, the Laplacian velocity field of a three-dimensional pipe flow can be solved with the CFD techniques. To model the gravitational field of one mass body, the pipe needs to be transformed following the procedure shown in Fig. 5. In this way, one can obtain a special pipe that only contains one inlet and one outlet (Fig. 5g). The inlet is a sphere with the center located at the center of mass (hereafter referred to as outer sphere), and the outlet is the mass surface. Due to the interchangeability of the gravitational vector $\varvec{g}$ and the potential flow velocity $\varvec{v}$, the fundamental equations of the gravitational field determination problem are given by Eqs. (9) and (11)

• Governing equations:

  $$\begin{aligned} \left\{ \begin{matrix} \nabla \cdot \varvec{g}=0 \\ \varvec{g}\cdot \nabla \varvec{g}=-\nabla p \\ \end{matrix} \right. \end{aligned}$$

  (30)

• Boundary condition:

  $$\begin{aligned} p=-\frac{1}{2}{{g}^{2}} \end{aligned}$$

  (31)

Note that to calculate the boundary value p, only the scalar gravitation, $g=\left| {\varvec{g}} \right|$, is needed. The scalar gravitation on the outer sphere, whose radius is set to be ten times the average size of the mass body, is assumed to be homogeneous and calculated with Newton’s formula, $\frac{{GM}}{{{r^2}}}$ , by viewing the mass body as a condensed point with the total mass M. The outer sphere as well as the homogeneous boundary value is a boundary condition more practical than the regularity condition at infinity, and they are consistent to each other when the radius of the outer sphere approaches infinity. For the proof and explanation on this issue, see “Appendix A”. In parallel, the scalar gravitation on the mass body surface can be obtained through two ways, either by direct measurement or by integration from an assumed density distribution.

3 Example: Comet 67P/Churyumov–Gerasimenko

There are two goals for the case study. One is to derive a fully convergent gravitational field solution of the comet 67P with the CFD techniques, and the other is to validate the performance of the new method in solving the CBVPs. The comet 67P is chosen as the case study, because few previous CBVP-solving methods are able to solve the gravitational field of such a complex-shaped mass body for its fully convergent solution, and demonstrating the validity of the CFD technique in such a highly challenging environment should create trust in the methodology.

3.1 Data

The comet 67P has an irregularly shaped body like a “rubber duck” and has been the target of ESA’s comet-chasing Rosetta mission. The Rosetta spacecraft obtained spectacular images with the narrow angle camera (NAC) and the wide angle camera (WAC)

Table 3 Basic information of the comet 67P/Churyumov–Gerasimenko (ESA 2016)

(Sierks et al. 2015), in order to build the shape model of the comet 67P. The shape model we adopt is developed by ESA’s Rosetta archive team, consisting of 104 207 faces, matching NVC image data gathered up to October 2016, and released under the Creative Commons licence of ESA/Rosetta/NAVCAM -CC BY-SA IGO 3.0. Figure 6 shows the double-lobed comet model, and Table 3 gives the basic information of the two-lobe nucleus. The shape model can be downloaded from https://imagearchives.esac.esa.int/index.php?/page/navcam_3d_models. Additionally, since gravitational measurements do not exist on the comet surface, observations are simulated on the basis of an assumed constant density $\rho =533.0\,\mathrm {kg/m^3}$ (Paetzold et al. 2016).

Fig. 7

Workflow of the comparison between the CFD solution and the Newton integration. Both branches are simulated from two input data: the shape and the density models. The interior and the exterior meshes are generated separately. The mass of each interior tetrahedron is assumed to be condensed as a point mass at the centroid for the subsequent Newton integration

3.2 Scheme

The case study is conducted in a closed-loop simulation. As shown in Fig. 7, two solutions (i.e., one obtained from the new method and the other a benchmark) are derived through two branches, starting from the common input (i.e., the shape and the density models) and finally compared to each other. For the branch of the CFD method, firstly the scalar surface gravitation, $g = \left| {\varvec{g}} \right|$, is simulated by integrating the assumed density, $\rho =533.0\,\mathrm {kg/m^3}$, and then the boundary value (i.e., pressure) is calculated with Eq. (31), $p =-\frac{1}{2}{{g}^2}$, and finally the gravitational solution is derived with the CFD techniques (see Sect. 2). Note that the radius of the outer sphere is taken to be ten times the average size of the comet, and the scalar gravitation on it is generated homogeneously with Newton’s formula, $\frac{{GM}}{{{r^2}}}$, by viewing the comet as a point with the total mass of M. The reason for the radius determination is explained in “Appendix A”. For the benchmark solution, a direct integration is performed with Newton’s formula, in which the interior region of the comet is meshed into 261 628 control volumes, each with an average size of $\sim$ 100 m, and the exterior region is meshed into 457 793 control volumes, with an increasing size from the comet’s surface to the outer sphere. Figure 8b shows an example of the interior mesh with large size for the illustration purpose. Both the interior and the exterior meshes adopt unstructured tetrahedrons in the case study, due to their better performance on meshing irregular bodies (Fig. 8a), compared to the structured ones as illustrated in Sect. 2.3. The mesh generator and the numerical solver used in this study are ICEM CFD 18.2 and ANSYS FLUENT 18.2, respectively.

Fig. 8

Unstructured mesh configuration for the purpose of result comparison between the new method and the Newton integration. a The exterior mesh and b the interior mesh of the comet 67P. In b, the interior region of the comet is meshed with large cells for demonstration; the actual number of the interior mesh cells used in the case study is 261 628

The benchmark solution in this study is not the true gravitational field but an approximated one of the comet 67P, with the errors coming from three sources: the geometrical model, the homogeneous density assumption and the integration scheme. The former two are data/model errors, while the last one is due to the inherent property of the numerical integration. That is, the benchmark gravitational field (defined at the exterior centroids of the tetrahedrons as shown in Fig. 8a) is generated by integrating the attractions of the integral interior mass elements, each condensed at its centroid as a mass point. Only if all integral mass volumes tend to become infinitesimal, the overall benchmark gravitational field would approach the true value. However, the approximated gravitational field is a valid benchmark example in this case study for three reasons. First, the benchmark keeps the main feature of the true gravitational field and has little influence on the investigation goal of the case study. Second, the benchmark is analytical, albeit in an integral form, so that it is easy to be calculated. Third, the benchmark is generated in a closed-loop validation scheme, and the workflow has no relation to the true gravitational field (Fig. 7).

3.3 Results

With the input data and a proper CFD configuration, the SIMPLE algorithm takes $\sim$ 10 min (corresponding to  600 iterations) to converge to an optimal solution. We then plot the three-dimensional gravitational vector field (Fig. 9) together with its four cross sections (Fig. 10), the plumb line distribution (Fig. 11) and the surface scalar gravitation (Fig. 12). Note that the boundary information of the comet 67P (e.g., the scalar gravitation) remains unchanged before and after the CFD calculation.

Fig. 9

Gravitational field of the comet 67P. In a to d, the vectors are potential-flow velocities in the fluid domain. The velocities are solved for with the CFD techniques and are equivalent to the gravitational vectors of the comet 67P in value

Fig. 10

Gravitational cross sections of the comet 67P. In a to d, the colored arrows indicate the gravitational vectors located in each cross-section plane, as determined by three clockwise numbers 1–3 in the sketch inset for each panel

Fig. 11

Plumb lines of the comet 67P. In a to d, each colored line represents one fluid particle’s path, as well as a stream line, derived with the CFD techniques. According to the conceptual mapping listed in Table 1, the stream lines of the potential flow are equivalent to the plumb lines of the gravitational field

Fig. 12

Scalar gravitation of the comet 67P. In a to d, the colored surface is the distribution of the scalar velocity of the potential flow which is equivalent to the scalar gravitation on the surface of the comet 67P. In this study, the scalar gravitation of the comet surface is obtained with the Newton integration, assuming the comet has a homogeneous density of 533.0 ${\mathrm {kg/}\mathrm {m}^3}$

The resulting gravitational field is qualitatively consistent with the real-world experience. For example, the vector magnitudes decrease with increasing distance from the mass surface, with an approximately reciprocal relation, while not as simple as that revealed by the Newtonian gravitational inverse square law (see Fig. 10). The complexity of the gravitational field can be observed from the plumb-line distribution (Fig. 11), showing a prominent curvature near the body’s surface. The realization of such a complex gravitational field, especially the gravitational structure close to the body surface, may have several applications in the future, e.g., the landing trajectory determination for a deep-space probe. Refer to Sect. 4.2 for a detailed discussion on this topic. Further interesting and natural characteristics of the comet’s gravitational field are the locations of maximum and minimum gravitation. The points of maximum gravitations are located at both ends of the comet (in the long dimension of the mass; see Figs. 10c, d, and 12a, d), because for either face all the masses are located on one side thereby maximizing the attraction thereon; the minimum gravitation is located at the neck between the two lobes (see Figs. 10c, d and 12b, c), because the gravitational forces caused by the two lobes cancel out to a maximum extent compared to other parts. These features are consistent with the qualitative analysis based on Newton’s law.

In order to compare the CFD solution (velocity vectors denoted as $\varvec{v}$) and the integration benchmark (gravitational vectors denoted as $\varvec{g}$), we use the following three indicators:

• Absolute magnitude error

  $$\begin{aligned} \Delta g =\left| {\left| {\varvec{v}} \right| - \left| {\varvec{g}} \right| } \right| \end{aligned}$$

  (32)

• Relative magnitude error

  $$\begin{aligned} \Delta e = \left| {\frac{{\left| {\varvec{v}} \right| - \left| {\varvec{g}} \right| }}{{\left| {\varvec{g}} \right| }}} \right| \end{aligned}$$

  (33)

• Angular difference

  $$\begin{aligned} \Delta \theta = \arccos \frac{{{\varvec{v}} \cdot {\varvec{g}}}}{{\left| {\varvec{v}} \right| \left| {\varvec{g}} \right| }} \end{aligned}$$

  (34)

The above three indices evaluate the differences of absolute magnitude, relative magnitude and relative direction between the CFD solution and the benchmark example, with smaller values indicating a better consistence of them. Figure 13 shows the histograms for a total of 457 793 checking points as defined at the centroids of the exterior finite volume elements (see Fig. 8a). As shown in Fig. 13, the gravitational magnitude of the comet 67P ranges between 0 and $\sim$ 25 mGal, with a mean value of 8.03 mGal (Fig. 13a), and the root-mean-square (RMS) of the absolute magnitude differences is merely 0.19 mGal (Fig. 13b), indicative of the consistence of the two solutions. The consistence can also be observed from the histograms of the relative magnitude error and the directional difference. As shown in Fig. 13c, d, the overall magnitude of the relative errors is smaller than 0.10, i.e., at a few percent level, and the angular difference is within $5^{\circ }$. Their RMS values are 0.02 and $0.78^{\circ }$, respectively.

Fig. 13

Histograms of a the gravitational field magnitude, b the absolute magnitude error, c the relative magnitude error and d the directional difference between the CFD solution and the Newton integration. Red lines mark their mean/RMS values. For the mathematical expressions of the four indicators, refer to Eqs. (32)–(34)

4 Discussion

The new method of this study established an equivalence between the gravitational field and the potential flow, implying that the gravitational field can be viewed as a stationary potential flow. Interestingly, in the CFD community, such an ideal fluid flow is thought impossible to occur in the real world, because realistic fluid flows are more or less viscous; however, the potential flow model is a great concept for solving the challenging CBVPs in geodesy. To support this viewpoint, we discuss two aspects of the new method: key success factors for solving CBVPs and its potential applications in asteroid exploration.

4.1 Key success factors for solving CBVPs

This study derives a new mathematical formulation for gravitational field modeling, i.e., the governing equation (30) and the boundary condition (31). They serve as a new theoretical basis for the gravitational field modeling problems, instead of the regular ones, i.e., the Laplace equation and the fundamental equation of physical geodesy. The governing equation of the new method has a mathematical form more complex than that of the Laplace equation, while the expression of the boundary condition is simpler than that of the fundamental equation of physical geodesy, only containing scalar gravitation. The observability of scalar gravitation allows the new method to be free of perturbation theory and is a critical success factor for solving the CBVPs. The reason is illustrated as follows.

As shown in Fig. 14, all of the solvable gravitational fields form a solution space (denoted as S), with each interior point representing a gravitational field. A specific gravitational field modeling method corresponds to a subsolution space, which covers the optimal point ${{\varvec{{\tilde{g}}}}_ \bot }$ (i.e., the projection point of the true gravitational field ${{\varvec{{\tilde{g}}}}}$) if it is able to derive the optimal solution. Perturbation methods need a reference gravitational field, ${{\varvec{g}}_{\varvec{0}}}$, of an analytical form, such as the gravitational field of a ball, a revolution ellipsoid or a triaxial ellipsoid with a homogeneous density. Exemplified with the spherical harmonics inversion method (see Table 1), during the series convergence process, an estimated spherical harmonic solution ${{\varvec{{\hat{g}}}}}$ initiates from the reference gravitational field ${{\varvec{g}}_{\varvec{0}}}$ and approaches the optimal solution ${{\varvec{{\tilde{g}}}}_ \bot }$. In general, the complexity of the true gravitational field ${{\varvec{{\tilde{g}}}}}$ is arbitrary, indicated by the difference between the optimal gravitational solution and the reference gravitational field, $\left| {{{{\varvec{{\tilde{g}}}}}_ \bot } - {{\varvec{g}}_{\varvec{0}}}} \right|$. The hyperball with the center point of ${{\varvec{g}}_{\varvec{0}}}$ and the radius of ${r_0}$ represents the linearity valid region of the perturbation method. Any point (denoting a gravitational field) within the hyperball can be linearly expanded from the reference point (i.e., the reference gravitational field ${{\varvec{g}}_{\varvec{0}}}$). In other words, a specific perturbation method is only applicable to the gravitational fields within its solution space (i.e., a hyperball like that in Fig. 14). Under this framework, the gravitational field determination problem can be understood as to find an estimated solution ${{\varvec{{\hat{g}}}}}$, as close as possible to its optimal value ${{{\varvec{{\tilde{g}}}}}_ \bot }$. Depending on the complexity of the unknown (true) gravitational field ${{\varvec{{\tilde{g}}}}}$, the location of the optimal gravitational field ${{{\varvec{{\tilde{g}}}}}_ \bot }$, with respect to the reference model ${{\varvec{g}}_{\varvec{0}}}$, has two possibilities: $\left| {{{{\varvec{{\tilde{g}}}}}_ \bot } - {{\varvec{g}}_{\varvec{0}}}} \right| \le {r_0}$ or $\left| {{{{\varvec{{\tilde{g}}}}}_ \bot } - {{\varvec{g}}_{\varvec{0}}}} \right| > {r_0}$. The former corresponds to cases applicable with the perturbation theory, while the latter does not. Figure 14 shows that the interior region of the hyperball occupies a small portion of the solution space, indicating a limited power of perturbation methods in solving CBVPs, although they are widely used in current geodetic methodology.

Fig. 14

The convergence process of an estimated gravitational field starting from the reference gravitational field to an optimal solution. The grey disk corresponds to a hyperball whose inner points represent the gravitational fields that can be solved only with the perturbation theory. By contrast, the new method of this study is able to break the limit of perturbation methods and solves more complex gravitational fields, i.e., those outside the hyperball

The limited capability of solving CBVPs is an obstacle met by the existing gravitational field modeling methods, especially those based on the Laplace equation. In fact, the gravitational field modeling methods founded on the Laplace equation, in both analytical and numerical forms, are in a dilemma currently, regarding whether or not to abandon the perturbation theory when dealing with CBVPs. On the one hand, as analyzed above, the perturbation theory limits the ability of solving CBVPs. To overcome this weakness, it seems one needs to abandon the perturbation theory. On the other hand, the perturbation theory serves as a hinge of the gravitational field modeling workflow, because it helps to incorporate gravitation observations by constructing gravity disturbance $\delta g$ or gravity anomaly $\Delta g$ as the boundary value. From this point, it seems one needs to insist on the perturbation theory. Without better choices to solve the CBVPs, the dilemma pushes geodetic researchers to make efforts in modifying or improving the Laplace equation based methods, albeit built on the perturbation theory. We consider this as an important reason for the current unsatisfying state of addressing the CBVPs. Hopefully, the new method has a potential to break the dilemma due to the following reasons.

From the theoretical perspective, the new method is not a perturbation method and is able to solve the CBVPs. The continuity, momentum and energy equations of the potential flow are derived as the fundamental equations of the new method, employing the gravitational vector ${{\varvec{g}}}$, instead of gravity disturbance $\delta g$ or gravity anomaly $\Delta g$, as the unknown, which frees the new method from the perturbation theory. Then, applying the SIMPLE algorithm to the potential flow problem, one can obtain a Laplacian velocity field, i.e., the equivalent solution of the gravitational vector field. As illustrated in Fig. 14, when solving the potential flow problem with the SIMPLE algorithm, the estimated solution ${{\varvec{{\hat{g}}}}}$ is able to get out of the hyperball (perturbation theory valid region) to approach the optimal solution ${{{\varvec{{\tilde{g}}}}}_ \bot }$, for the CBVP cases, i.e., $\left| {{{{\varvec{{\tilde{g}}}}}_ \bot } - {{\varvec{g}}_{\varvec{0}}}} \right| > {r_0}$. For the proof of the Laplacian property of the potential flow velocity field, refer to “Appendix B”.

From the technical point of view, two factors are thought to be critical. First, the numerical scheme (i.e., the CFD techniques) is adopted, which facilitates not only the definition of the computational domain (i.e., the exterior space of a complex shaped mass body) but also the assignment of the boundary value. Additionally, as pointed out in Sect. 1, numerical methods are better at solving highly nonlinear problems compared to analytical methods, and, in this study, the CFD techniques demonstrate a powerful capability in solving the CBVPs. Second, an intuitive figure of the gravitational field is constructed with the concepts of the potential flow. This is realized by building the conceptual equivalence between the potential flow and the gravitational field. With this idea, the abstract gravitational field can be better understood and the theories (e.g., Bernoulli’s theorem) and tools (e.g., the SIMPLE algorithm) from the CFD community can be introduced for solving the CBVPs of the gravitational research field. It is worth mentioning that the relevant theories and tools have cost great efforts of the CFD research community and it is fortunate to introduce them into geodesy. The discovery of the link between the two seemly unrelated research fields may be one important contribution of this study.

4.2 Potential applications in asteroid exploration

It is the first time to derive a fully convergent gravitational field for the complex-shaped comet 67P, in terms of a boundary value problem solution, which is different from those integration schemes in either spatial or spectral domains (e.g., Andert et al. 2015; Reimond and Baur 2016; Fukushima 2017, 2018; Hirt and Kuhn 2018; Wu et al. 2019, etc.). In theory, the new CBVP solving method can be applied to asteroid exploration missions, in which the target mass bodies usually have irregular shapes.

Asteroid exploration is an activity that represents the state of the art of deep space technology. In the past two decades, several advanced spacecraft have been launched to investigate small celestial bodies (including asteroids and comets). For example, European Space Agency (ESA) and Japan Aerospace Exploration Agency (JAXA) have successfully performed exploration missions for a comet (target: the comet 67P; spacecraft: Rosetta; project duration: 2004–2016) and an asteroid (target: the asteroid Itokawa; spacecraft: Hayabusa; project duration: 2003–2010), respectively. Currently, two asteroid exploration programs are ongoing: Hayabusa2 from JAXA (target: the asteroid Ryugu; project duration: 2014–2020) and OSIRIS-REx from National Aeronautics and Space Administration (NASA) (target: the asteroid Bennu; project duration: 2016–2023). The small celestial bodies have irregular shapes and generate gravitational fields that are weak and complex. A gravitational field model with a high precision plays an important role in an asteroid exploration mission, e.g., it can be used to determine hovering orbits or landing tracks of a probe. However, the geometrical information of the asteroid to be investigated is usually unknown until a spacecraft reaches it, making it a challenge to model a timely gravitational field during an asteroid exploration. Hopefully, the new method of this study has the potential to be applied in future asteroid exploration missions, for its two advantages:

(1) High computational efficiency

For the sake of explanation, the spherical harmonic (SH) inversion method is taken for a comparison analysis. The SH function has an analytical form and is computationally efficient when modeling gravitational fields of sphere-like bodies. However, when dealing with the gravitational field of a complex-shaped asteroid (i.e., solving the CBVP), the new method of this study, although as a numerical solving scheme, is superior to the SH inversion method in computational efficiency. This can be understood in the following way.

Taking the comet 67P for illustration, imagine that its two-lobe shaped mass body (see Fig. 1f for a schematic profile) can be transformed continuously from a ball (Fig. 1c). If the gravitational fields shown in Fig. 1c–f are applied with the SH inversion method, the truncation orders of the SH harmonics are expected to increase, because of the increasing complexity of the mass shape. Correspondingly, the calculation amounts increase as well. For example, the gravitational field of an inhomogeneous ball (Fig. 1c) only has a few number of harmonic components; however, for the comet 67P (Fig. 1f), it approaches infinity for the truncation order as well as the calculation amount, because the SH function is divergent. The SH series divergence implies that the comet 67P has a gravitational field whose complexity is already beyond the solving power of the SH inversion method. By contrast, our new method is not only able to model the gravitational field of the complex-shaped comet 67P, it also takes limited time, specifically, $\sim$ 10 min on a PC with the configuration of Windows 10 OS, Intel Core i7 and 64 GB RAM. In this sense, the new method has a high computational efficiency in solving the CBVPs and thus has a good application potential for asteroid exploration.

(2) Intuitive geometrical meaning

This study provides an intuitive perspective to view the gravitational field. With the conceptual mapping listed in Table 1, the abstract gravitational field can be visualized as a stationary potential flow, e.g., in terms of vectors or plumb lines (see Figs. 9, 10, 11). These geometrical elements are complementary to the equipotential surfaces as widely used in the Laplace equation based methods. The intuitive visualization of the gravitational field is expected to facilitate some tasks involved in an asteroid exploration mission, such as the design of a probe’s orbits around the body or landing tracks, the determination of an asteroid height system, the gravitational field modeling for multi-bodies, etc. The three potential applications are briefly outlined below.

• Design of a probe’s orbits or landing tracks

  Designing precise orbits or landing tracks of a probe is critical for the activities in an asteroid exploration mission, such as surface mapping, geometrical modeling and rock sampling, etc. The new method deals with the gravitational field modeling problem in spatial domain, thereby enabling a visual devise of a probe’s orbits or landing tracks. It is more convenient to design orbits or tracks in the spatial domain than in the spectral domain, due to two reasons. First, the convergence and accuracy of a gravitational field solution can be assessed directly in the spatial domain, which is usually hard for spectral-domain methods (e.g., the SH inversion method). Second, the spatial gravitational field solution, in either vectorial or plumb-line form, enables a convenient analysis of the probe’s force state at transient positions, followed by the determination of its moving paths.

• Determination of an asteroid height system

  Determining a precise asteroid height system is expected to benefit exploration activities. In general, a height system consists of two key factors: (1) a reference surface (i.e., the zero-level equipotential surface) and (2) height continuation paths. For conventional height systems, the reference surface usually adopts a geoid, which is mostly beneath the body surface (e.g., the Earth), and the relevant continuation algorithms are of upward type.

  The geoid determination problem for a spheroid mass body (e.g., the Earth) is already rather challenging in physical geodesy, and building height systems for irregularly shaped asteroids should be even more difficult. We believe that the new method provides a possible solving scheme, for example, to take the outer sphere (see Fig. 5) and the plumb lines (see Fig. 11) as the reference (equipotential) surface and the downward continuation paths, respectively. However, the realization of this idea needs far more analysis.

• Gravitational field modeling for multi-bodies

  Prior to this study, modeling the gravitational field caused by one complex-shaped mass body (i.e., the single-body CBVP) is already tricky enough, not to speak of the multi-body CBVP. In theory, the multi-body CBVP can be solved with our new method, because, from the perspective of the potential flow, the single- and multi-body CBVPs are fundamentally the same except for the number of outlets, each representing one mass body surface. Solving the multi-body CBVP may contribute to deep-space exploration missions in the future.

5 Conclusion and outlook

A new gravitational field modeling method is proposed in this research, elaborated in both theoretical and application aspects:

• A new mathematical formulation for modeling gravitational fields is derived from potential flow theory, including the governing equations (30) and the boundary condition (31). The new fundamental equation set is equivalent to the Laplace equation when expressing a gravitational field, both referring to harmonic potential fields or Laplacian vector fields. The Laplacian property of the potential flow’s velocity field is mathematically proved. The new formulation is analytical, and the way of solving the BVP is numerical. It has the great advantage of circumventing perturbation theory which is the theoretical basis of conventional methods.

• CFD techniques are introduced as numerical tools to solve the new fundamental equation set, and a CFD workflow is devised for the gravitational field modeling. To validate the new method, the challenging gravitational field of comet 67P is taken as example. It is the first time to solve a gravitational field with the complexity level of comet 67P and without any divergence problem. A CFD solution is derived based on our method, and a direct integration of Newton’s formula is generated as a benchmark. Their comparison shows a magnitude difference at the level of a few percent and the directional difference RMS value of $0.78^{\circ }$.

It should be emphasized that a conceptual bridge (i.e., a conceptual mapping) between the gravitational field and the potential flow is proposed in this study, and the proof-of-concept, from both theory and application aspects, is provided. To realize a relatively quick proof-of-concept, the commercial (academic) version of the CFD software ANSYS FLUENT is used in this study. However, it limits the mesh number up to 512 000, almost reached in the case study. Hence, the gravitational field of the comet 67P derived in this study still can be improved in terms of accuracy. To break the mesh number limit, one promising scheme is to develop an open-source code with the free CFD software OpenFOAM. In that way, the new method can be studied in flexible ways and on various aspects, such as precision improvement, spatial resolution optimization, and computational efficiency enhancement. In addition, the integration of measurements from other boundaries (e.g., the observations from satellite gravimetry) may also be a necessary improvement for the new method.

In summary, this study derives a new CBVP solving method, and, from both theoretical and practical points of view, it has a good performance on solving the CBVPs, overcoming the divergence problem of conventional approaches. Moreover, a large number of follow-on studies can be defined for the perfection of the new method and we have a confident outlook on its future applications.

Appendices

Appendix A

1.1 Proof of the regularity condition at infinity

Conventional gravitational field modeling methods are usually formulated in terms of an exterior boundary value problem. The Laplace equation is solved in a perturbative approach, in which the unknown disturbing potential satisfies two boundary conditions: (1) the fundamental equation of physical geodesy on an approximative surface (e.g., a geoid or a mass body surface, respectively, involved in the Stokes and the Molodensky solutions) and (2) the regularity at infinity. By contrast, the CFD method of this study treats the exterior space of a mass body as the interior region of a pipe and manipulates the potential flow problem with the CFD techniques. In the potential flow problem, there are two boundaries, i.e., the body surface and the outer sphere (see Fig. 5), both subject to the boundary condition defined in Eq. (31).

Comparing conventional methods with the one of this study, a common point is that the near-body surface is taken as one boundary, while the distant boundaries of them are different. For conventional methods, the distant boundary refers to an infinite surface on which the gravitational potential is zero, but for the new method, the distant boundary is the outer sphere with the boundary value of Eq. (31). In fact, as the radius of the outer sphere approaches infinity, the scalar gravitation g as well as the boundary value $- \frac{1}{2}{{g}^{2}}$ on it tends to be zero, indicating that the gravitational field solved with the new method satisfies the regularity condition at infinity as well. However, it should be noticed that the variables involved in the two regularity conditions are different (i.e., the gravitational potential and the scalar gravitation) and they govern different aspects of a gravitational field.

From a theoretical point of view, the new method should adopt an outer sphere with an infinitely large radius, which, however, is impractical because of the unrealistic amount of meshes as well as computation. Instead, an outer sphere with a limited radius is constructed in the new method, with the gravitation thereon calculated with Newton’s formula, $\frac{{GM}}{{{r^2}}}$, which is actually the zero-degree radial gravitation of a gravitational field:

$$\begin{aligned} g\left( {r,\theta ,\lambda } \right) = \frac{{GM}}{{{r^2}}} + \sum \limits _{n = 2}^\infty {\frac{{n + 1}}{R}{{\left( {\frac{R}{r}} \right) }^{n + 2}}{V_n}\left( {\theta ,\lambda } \right) } \end{aligned}$$

(A.1)

where $V\left( {r,\theta ,\lambda } \right)$ and $g\left( {r,\theta ,\lambda } \right)$ denote the gravitational potential and the radial gravitation, respectively, defined at points in spherical coordinates $( {r,\theta ,\lambda })$, and R is the radius of a reference sphere, which is taken to be the average size of the mass body in this study. Note that the first-degree harmonic component (i.e., $n=1$) does not exist in Eq. (A.1) because the origin of the coordinate system is already placed at the center of mass.

In this study, the setup of the outer sphere as well as its boundary value is essentially a substitute of the regularity condition at infinity, although an approximation is involved, i.e., the sum of the high-degree gravitational components (see Eq. (A.1)) is omitted as if it is an error. The approximation effect can be suppressed with a large enough radius of the outer sphere, because, as the radius increases, the high-degree components decrease faster than the zero-degree one, each with a decay depending on the factor ${\left( {\frac{R}{r}} \right) ^{n + 2}}$.

As can be seen from the above analysis, the radius of the outer sphere can be neither too large nor too small, on account of the balance between the computational amount and the approximation influence. Therefore, determining a proper radius for the outer sphere is critical, and in this study we set it to be ten times the average size of the mass body (i.e., $r = 10R$; see Fig. 7) for the following two reasons.

First, from the theoretical side, we draw on Saint-Venant’s principle to determine the minimum value of the radius. In elastic theory, the Saint-Venant principle states that high-order moments of mechanical load (i.e., moments with orders higher than torque) decay so fast that they never need to be considered for regions far from the short boundary. The Saint-Venant principle can be applied to gravitational problems in theory, because a gravitational field is equivalent to a potential flow, and potential fluids can be regarded as an extreme case of elastic material (i.e., it is incompressible and frictionless). In terms of Saint-Venant’s principle, the inhomogeneous effect of a gravitational field only concentrates near a mass body, and the distant observations are like those generated by a mass point. Empirically, in elastic theory, one often takes for the large distance three times the average size of the mechanical load. Therefore, for gravitational problems, the radius of the outer sphere should be at least three times the average size of the mass body.

Second, from the practical side, tests have been conducted for validating the chosen radius. We take the radius of the outer sphere as ten times the average size of the mass body and calculate two sets of boundary values. One is inhomogeneous, based on the gravitational integration, and the other is homogeneous, calculated with Newton’s formula. The two sets of boundary values show a good consistency and only differ from the third valid digit, which is thought to be acceptable for the concept-of-proof goal.

In summary, it is a robust strategy to set the radius of the outer sphere to be ten times the average size of the mass body. However, it is also worth noticing that a very large outer sphere radius may cause the testing indices (33) and (34) to become artificially small, due to the inclusion of similar gravitational vectors in distant regions. Therefore, the determination of a more rigorous radius for the outer sphere needs further investigations in the future.

Appendix B

1.1 Proof of the Laplacian property of the potential-flow velocity field

In Sect. 2.2 of the main text, imposing the constraints listed in Table 2 on Newtonian flow yields the fundamental equations of the potential flow, and the Laplacian property (i.e., source-free and curl-free) of the potential flow velocity field is analyzed from the physical perspective. In this part, we will give a rigorous mathematical proof of the statement that the velocity solution of the potential-flow fundamental equation, solved with the SIMPLE algorithm, is Laplacian. Mathematically, one needs to prove the following relation:

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {\nabla \cdot {\varvec{v}} = 0}\\ {{\varvec{v}} \cdot \nabla {\varvec{v}} = - \nabla p}\\ {p = - \frac{1}{2}{v^2}} \end{array}} \right. \mathrm{{ }} \Rightarrow \mathrm{{ }}\left\{ {\begin{array}{*{20}{c}} {\nabla \cdot {\varvec{v}} = 0}\\ {\nabla \times {\varvec{v}} = {\varvec{0}}} \end{array}} \right. \end{aligned}$$

(B.1)

in which the former equation set contains the fundamental equations of the potential flow, to be solved with the SIMPLE algorithm in this study, and the latter one defines Laplacian vector fields.

Proof

First of all, it is necessary to make clear the proof logic.

A regular way of proving relation (B.1) is to prove the set inclusion relation, ${S_\mathrm {PF}} \subset {S_\mathrm {L}}$, where $S_\mathrm {PF}$ is the potential-flow solution set and $S_\mathrm {L}$ is the Laplacian vector set, respectively, corresponding to the two equation sets in relation (B.1). As will be seen later, the set relation, ${S_\mathrm {PF}} \subset {S_\mathrm {L}}$, is not satisfied, but the opposite one, ${S_\mathrm {L}} \subset {S_\mathrm {PF}}$, holds. Hence, if relation (B.1) is correct, additional constraints should be considered, and consequently the following three facts need to be proved.

• 1) The research objects to be solved (i.e., gravitational vector fields) exist and be Laplacian;

• 2) The Laplacian vector space belongs to the potential-flow solution space, i.e., ${S_\mathrm {L}} \subset {S_\mathrm {PF}}$;

• 3) The potential flow solution derived with the SIMPLE algorithm is unique.

The proof logic is explained in Fig. 15, in which if the above three facts are true, the unique potential-flow velocity solution, derived with the SIMPLE algorithm, has to be the gravitational vector solution which is Laplacian.

Fig. 15

Illustration of the Laplacian property (i.e., source-free and curl-free) of the potential-flow velocity field derived with the SIMPLE algorithm

The fact of the first item is evident because the research objects of this study are existing gravitational fields and they can be projected into the Laplacian vector space. The statement of the third item is true, on account of the well-posedness of the SIMPLE algorithm, as well as the fact that no additional artificial constraints are introduced, when solving the potential flow problem.

As for the second item, the set inclusion relation, ${S_\mathrm {L}} \subset {S_\mathrm {PF}}$, holds because of the identity (Schey 1973)

$$\begin{aligned} {\varvec{v}} \cdot \nabla {\varvec{v}} - \nabla \left( {\frac{1}{2}{v^2}} \right) \equiv - {\varvec{v}} \times \left( {\nabla \times {\varvec{v}}} \right) = \varvec{0} \end{aligned}$$

(B.2)

to which the curl-free property of Laplacian vector fields, $\nabla \times \varvec{v} = \varvec{0}$, is applied. Note that the derived identity, ${\varvec{v}} \cdot \nabla {\varvec{v}} = \nabla \left( {\frac{1}{2}{v^2}} \right)$, is a combination of the momentum equation, ${{\varvec{v}} \cdot \nabla {\varvec{v}} = - \nabla p}$, and the boundary condition, $p = - \frac{1}{2}{v^2}$, of the potential flow.

Up to this point, the three facts have been proved, and hence, the Laplacian property of the potential flow’s vector field solved with the SIMPLE algorithm has been proved as well.

Before ending this appendix, an explicit form of the potential-flow solution space, $S_\mathrm {PF}$, is given below by solving the fundamental equation set of the potential flow (i.e., the first equation set in relation (B.1)). To achieve this goal, one needs to solve the following equation

$$\begin{aligned} {\varvec{v}} \times \left( {\nabla \times {\varvec{v}}} \right) = \varvec{0} \end{aligned}$$

(B.3)

The above equation is correct because of Eq. (B.2), to which the identity, ${\varvec{v}} \cdot \nabla {\varvec{v}} = \nabla \left( {\frac{1}{2}{v^2}} \right)$, of the potential flow is applied. Then, according to the calculation rule of cross products, Eq. (B.3) can be rewritten as

$$\begin{aligned} \left| \varvec{v} \right| \left| {\nabla \times \varvec{v}} \right| \sin \theta = 0 \end{aligned}$$

(B.4)

where $\theta$ is the angle between the velocity ${\varvec{v}}$ and its curl ${\nabla \times \varvec{v}}$. Solving Eq. (B.4) yields

$$\begin{aligned} {S} = S_{1} \cup S_{2} \cup S_{3} \end{aligned}$$

(B.5)

where ${S_1} = \left\{ {\left. {\varvec{v}} \right| {\varvec{v}} = {\varvec{0}}} \right\}$, ${S_2} = \left\{ {\left. {\varvec{v}} \right| \nabla \times {\varvec{v}} = {\varvec{0}}} \right\}$ and ${S_3} = \left\{ {\left. {\varvec{v}} \right| {\varvec{v}}\parallel \nabla \times {\varvec{v}}} \right\}$. Redividing the above solution space and taking into account the continuity equation, ${S_\mathrm {C}} = \mathrm{{\{ }}\left. {\varvec{v}} \right| \nabla \cdot {\varvec{v}} = 0\mathrm{{\} }}$, generates the potential-flow solution space as follows:

$$\begin{aligned} {S_\mathrm {PF}} = S_\mathrm {PF}^1 \cup S_\mathrm {PF}^2 = \left[ {{S_\mathrm {C}} \cap \left( {{S_1} \cup {S_2}} \right) } \right] \cup \left[ {{S_\mathrm {C}} \cap {S_\mathrm {3}}} \right] \end{aligned}$$

(B.6)

where $S_\mathrm {PF}^1\mathrm{{ = \{ }}\left. {\varvec{v}} \right| \nabla \cdot {\varvec{v}} = 0 \ ;\ \nabla \times {\varvec{v}} = \varvec{0}\mathrm{{\} }}$ and $S_\mathrm {PF}^2\mathrm{{ = \{ }}\left. {\varvec{v}} \right| \nabla \cdot {\varvec{v}} = 0\ ;\ {\varvec{v}}\parallel \nabla \times {\varvec{v}}\mathrm{{\} }}$. Figure 15 shows the potential-flow solution space, $S_\mathrm {PF}$, and its relation to other solution spaces. It is worth noticing that one subsolution space of the potential flow is actually the Laplacian vector space, i.e., $S_\mathrm {PF}^1 = S_\mathrm {L}$, so that ${S_\mathrm {L}} \subset {S_\mathrm {PF}}$, which is consistent to the second fact aforementioned. $\square$