Abstract
We derive an empirical model of the sub-daily polar motion (PM) based on the multi-GNSS processing incorporating GPS, GLONASS, and Galileo observations. The sub-daily PM model is based on 3-year multi-GNSS solutions with a 2 h temporal resolution. Firstly, we discuss differences in sub-daily PM estimates delivered from individual GNSS constellations, including GPS, GLONASS, Galileo, and the combined multi-GNSS solutions. Secondly, we evaluate the consistency between the GNSS-based estimates of the sub-daily PM with three independent models, i.e., the model recommended in the International Earth Rotation and Reference Systems Service (IERS) 2010 Conventions, the Desai–Sibois model, and the Gipson model. The sub-daily PM estimates, which are derived from system-specific solutions, are inherently affected by artificial non-tidal signals. These signals arise mainly from the resonance between the Earth rotation period and the satellite revolution period. We found strong spurious signals in GLONASS-based and Galileo-based results with amplitudes up to 30 µas. The combined multi-GNSS solution delivers the best estimates and the best consistency of the sub-daily PM with external geophysical and empirical models. Moreover, the impact of the non-tidal spurious signals in the frequency domain diminishes in the multi-GNSS combination. After the recovery of the tidal coefficients for 38 tides, we infer better consistency of the GNSS-based empirical models with the new Desai–Sibois model than the model recommended in the IERS 2010 Conventions. The consistency with the Desai–Sibois model, in terms of the inter-quartile ranges of tidal amplitude differences, reaches the level of 1.6, 5.7, 6.3, 2.2 µas for the prograde diurnal tidal terms and 1.2/2.1, 2.3/6.0, 2.6/5.5, 2.1/5.1 µas for prograde/retrograde semi-diurnal tidal terms, for the combined multi-GNSS, GPS, GLONASS, and Galileo solutions, respectively.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Polar motion (PM) is a wobble of the spin axis of the Earth about its figure axis. In space geodesy, PM is observed as a variation in the true pole at the surface of the Earth, represented by the pole coordinates, around the mean pole. The International Earth Rotation and Reference Systems Service (IERS) Conventions (Petit and Luzum 2010) classify the pole coordinates together with the Universal Time (UT1) as Earth rotation parameters (ERPs). The multi-scale variations in Earth rotation can be separated into nearly sub-daily signals (periods < 2 days), which used to be described as ultra-rapid variations in PM (Sibois et al. 2017), and longer-period fluctuations. The sub-daily variations in Earth rotation originate mainly from the redistribution and motion of masses of geophysical fluids, including the impact of solid Earth, hydrosphere (Gross et al. 2003; Ray et al. 1994), and atmosphere (Bizouard and Seoane 2010; Böhm et al. 2012; Brzeziński et al. 2002, 2004; de Viron et al. 2005).
The sub-daily ERP models are typically derived from ocean tide models based on altimetry data and supported by selected atmospheric tides (Petit and Luzum 2010; Desai and Sibois 2016; Madzak et al. 2016). The sub-daily ERPs can also be derived empirically using satellite and space geodetic techniques. All the space geodetic techniques including Global Navigation Satellite Systems (GNSS), Satellite Laser Ranging (SLR), Very Long Baseline Interferometry (VLBI), and Doppler Orbitography and Radiopositioning Integrated by Satellite (DORIS) are theoretically able to observe the PM. However, not all of them can deliver valuable information about its sub-daily variations, because of the technique-specific characteristics. The differences in the technique-specific estimates of sub-daily PM originate from different temporal resolution and abundance of observations, tracking data quality and susceptibility to biases, the complexity of data processing and separability of the estimated parameters, availability of well-distributed geometry of observations and reachable level of precision (Sibois 2011). Watkins and Eanes (1994) presented the sub-daily ERPs from SLR using a dataset from LAGEOS. VLBI has been used more extensively by Artz et al. (2010), Gipson (1996) and Haas and Wünsch (2006). The sub-daily ERPs from GPS were published by different groups (Hefty et al. 2000; Rothacher et al. 2001; Sibois et al. 2017; Steigenberger et al. 2006). Finally, some groups brought together the qualities of both VLBI and GPS techniques and provided results from combined solutions (Artz et al. 2012; Thaller et al. 2007). One of the main messages that the mentioned studies give is as follows: there is a non-trivial disagreement between the models based on different satellite or space geodetic techniques (Desai and Sibois 2016; Griffiths and Ray 2013). The inconsistency between the IERS2010 model and GNSS observations has been identified at the level of even 20% (Griffiths and Ray 2013; King et al. 2008). Furthermore, in the case of GNSS-based analysis, most of the recent studies refer to GPS-only solutions, whereas the analogous studies, which would cover other GNSS, such as GLONASS and Galileo, are not yet well described (Wei et al. 2015). Galileo and GLONASS have different revolution periods, thus, their sensitivity to sub-daily tides is different than that of GPS satellites, which additionally are affected by a deep resonance between the Earth rotation and the satellite revolution period. Moreover, owing to the increasing number of GNSS satellites, continuous observations, global coverage of stations, and increasing precision of the GNSS-based solutions, GNSS has the potential to outperform all other geodetic techniques in the estimation of high-frequency variations in PM.
Most studies focus on the sub-daily signals which are known from the theory of tides. On the other hand, the accuracy of the empirical models strongly depends on the identification of technique-specific errors and signals, which can affect the geophysical interpretation of the results. The empirically derived sub-daily ERP series include the total effect of both geophysical signals and technique-specific artifacts. For example, the GPS orbital period is close to the K2 tide; thus, the technique-specific error may almost completely be absorbed by the coupled tidal parameter (Hefty et al. 2000; Sibois et al. 2017). Since 2018, Galileo consists of 24 usable satellites in space (Hadas et al. 2019). With the constellation of 24 satellites, Galileo can be considered as nearly fully operational together with the legacy GPS (32 satellites) and GLONASS (24 satellites) systems (Table 1). Besides different revolution periods of various GNSS satellites, two Galileo satellites have an eccentric orbit, which may help to decorrelate tidal constituents from orbit parameters and reveal the GPS-based errors in sub-daily ERP estimates. The differences in global geodetic parameters delivered by different GNSS constellations have been already shown in the example of geocenter coordinates and daily ERPs (Meindl 2011; Scaramuzza et al. 2018; Zajdel et al. 2020, 2021). However, the aspect of sub-daily ERPs is barely discussed. The GNSS-related orbital signals, such as the systematic errors at harmonics of the GNSS draconitic periods, i.e., the repeat period of the satellite constellation w.r.t. the Sun, and satellite revolution periods, are expected to alias into the sub-daily ERPs (Abraha et al. 2018). That is mainly caused by the difficulties in precise orbit determination for different multi-GNSS satellites (Arnold et al. 2015; Prange et al. 2017; Bury et al. 2019; Dach et al. 2019; Rodriguez-Solano et al. 2014; Montenbruck et al. 2017). Hefty et al. (2000) already pointed out that several signals in the GPS-based time series could not be assigned to tidal signals, but are more likely caused by orbit modeling issues, especially solar radiation pressure (SRP) modeling.
This work focuses on both tidal and spurious non-tidal signals, which can be identified in the time series of sub-daily estimates of PM delivered from the GNSS processing. The main emphasis of this contribution is to evaluate the suitability of different GNSS constellations, including GPS, GLONASS, and Galileo, to the estimation of sub-daily PM and the reliability of the PM models based thereon. Additionally, we investigate the impact of different aspects of GNSS processing on the quality of sub-daily PM estimates, including different approaches of SRP modeling for Galileo orbits and the length of the orbital arcs: 1 day or 3 days. Finally, we assess the consistency of our empirical GNSS sub-daily PM models w.r.t. external models of sub-daily PM, including the IERS 2010 Conventions model (Petit and Luzum 2010), the Desai–Sibois model based on the altimetric ocean tide TPXO.8 model (Desai and Sibois 2016), and the Gipson model derived from VLBI data (Gipson 2017).
2 Methodology
In the following subsections, we introduce the methodology of the estimation of sub-daily PM from GNSS observations and outline the description of the solutions.
2.1 Processing strategy
The time series of sub-daily pole coordinates have been generated from multi-GNSS processing based on the observations collected by globally distributed networks of about 100 stations. All the stations track GPS, GLONASS, and Galileo; thus, we should not expect any differences in the results due to network effects (Zajdel et al. 2019). Background models used in the processing are summarized in Table 2. The processing strategy corresponds to the multi-GNSS processing as described by Prange et al. (2017) with a higher temporal resolution for the derived ERPs (Rothacher et al. 2001). We used the most recent version of Bernese GNSS Software (Dach et al. 2015), additionally modified to the purposes of multi-GNSS processing. The datum was realized using No-Net-Rotation and No-Net-Translation constraints w.r.t. IGS14 reference frame. The following parameters are set up and then estimated in the normal equation system: station coordinates, orbits, troposphere gradients, geocenter coordinates with 1-day resolution, ERPs, including X and Y pole coordinates and UT1-UTC, with 2 h resolution, and zenith troposphere delays with 2 h resolution. The ERPs were estimated adopting piece-wise linear parametrization. The UT1-UTC values are calculated in the processing; however, the first UT1-UTC parameters in the processing window are always highly constrained to the a priori values from the IERS-C04-14 series (Bizouard et al. 2018).
The sub-daily ERPs are estimated as precorrected series, thus with respect to the a priori model of sub-daily variations in ERPs including the effects of the oceans and libration consistently to the recommendations in IERS 2010 Conventions (Petit and Luzum 2010). Libration is a direct tidal torque that affects the Earth’s rotation and is caused by the tri-axial shape of the Earth, i.e., the deviation of the equator from a circle or the difference in the moments of inertia of the Earth (Mathews and Bretagnon 2003). As the libration is included a priori in the background model, the resulted estimates only account for the remaining effects. On the other hand, atmospheric effects, as well as high-frequency nutation, are neither modeled nor estimated in the solutions. Sibois et al. (2017) concluded that the estimation of the sub-daily ERPs in reference to the background model is recommended for GNSS processing, as it yields better estimates of the tidal constituents than the solution with no a priori ERP model. The official IERS-C04-14 series is also applied as a nominal model for the variations in ERPs with periods longer than 2 days. However, we should also be aware that IERS-C04-14 partly accumulates the errors of the IERS2010 model, as the IERS2010 model was presumably applied by most of the contributors to the IERS-C04 products (Desai and Sibois 2016).
Based on the conventional definition of the PM, the sub-daily retrograde PM variations with periods between − 1.5 and − 0.5 cycles per sidereal day, should be reflected as nutation, whereas all other variations are assigned to PM (Petit and Luzum 2010; Ray et al. 2017). The retrograde diurnal band of PM is then reflected by the IAU2006A nutation model (Mathews et al. 2002; Mathews and Bretagnon 2003), whereas retrograde and prograde semi-diurnal are always assigned to PM. When dealing with sub-daily ERP estimation using GNSS, one has to be aware of the correlation between the retrograde diurnal terms of PM and the orbit parameters. Every attempt to solve for sub-daily pole coordinates and Keplerian orbit parameters leads to a quasi-singularity of the normal equation systems (NEQs) due to the correlation between daily retrograde PM and orbital parameters including the inclination and the right ascension of the ascending node. Therefore, the retrograde diurnal polar motion is blocked at the NEQ level using a numerical filter and a zero-mean constraint (Hefty et al. 2000; Thaller et al. 2007).
2.2 Description of the solutions
Table 3 gives an overview of the analyzed solutions. In total, ten solutions have been derived. The preprocessing of observations with the residual screening has been made only once to maintain the consistency between all the solutions. Therefore, the differences between the solutions should reflect only the effect of a single change in the processing. The GRE solution stands for the multi-GNSS solution. The individual solutions have been made for GPS, GLONASS, and Galileo, to evaluate the quality of the sub-daily PM variations as seen by different GNSS constellations. These are called GPS, GLO and GAL for GPS, GLONASS and Galileo, respectively. The system-specific solutions are based on the same NEQs as described by Scaramuzza et al. (2018) and Zajdel et al. (2019). The ERPs, which are estimated in such a methodology directly, cast the system-specific signals, which arise from the changes in orbit quality and observational geometry for different GNSS constellations. On the other hand, the ERPs may also include some of the deficiencies, which would be transferred into other parameters, e.g., station coordinates, in the case of independent single-GNSS processing (Zajdel et al. 2020). Each of the mentioned solutions is calculated in the 1-day arc and 3-day arc processing regime to evaluate the impact of the arc-length on the sub-daily PM estimates. For the 3-day arc solutions, we use PM estimates from the middle day only, while the outer days were excluded from the analyses. The standard empirical approach for SRP modeling is employed using the extended Empirical CODE Orbit Model (ECOM2, Arnold et al. 2015), as it is handled by most of the Multi-GNSS Pilot Project (MGEX) Analysis Centers for their multi-GNSS products (Montenbruck et al. 2017). In all the ECOM2 solutions, three constant accelerations along three main satellite axes are estimated, D0, Y0, B0, together with once-per revolution sine and cosine parameters BS1, BC1, and twice-per-revolution parameters DS2, DC2. Additionally, we prepared one more Galileo-only solution labeled as GAB, to assess the impact of the change in SRP modeling on the sub-daily PM estimates (Table 3). The GAB solution employs the hybrid model for the SRP modeling, which combines the merits of both the empirical model and the analytical, simplified, macromodel of Galileo satellites. A box-wing macromodel for Galileo satellites can be generated since 2017 when the European GNSS Agency (GSA) released metadata (GSA 2017). The box-wing model for the GPS and GLONASS satellites can be also composed based on the selectively published GPS metadata (Fliegel and Gallini 1996) or empirically derived properties of the satellites (Rodriguez-Solano et al. 2012). The most recent and coherent information about the properties of the GPS and GLONASS satellites is provided in the frame of the IGS repro3 activities (http://acc.igs.org/repro3/PROPBOXW.f). However, we narrowed the analyzed set of hybrid SRP solutions to the Galileo system as a representative example, which as the only global constellation provides the official and publicly available metadata for the full constellation. The box-wing model absorbs up to 97% of direct SRP and allows for reducing the number of estimated empirical parameters (Bury et al. 2019). As a result, the set of periodic empirical parameters that are correlated with geodetic parameters can be reduced (Meindl et al. 2013). The selection of the set of empirical parameters, which should be chosen in the hybrid solution, is extensively studied by Bury et al. (2020). We deliberately decided to use the box-wing model with the classic set of ECOM parameters (Table 3) as it yields the best results for the orbits and daily ERPs (Zajdel et al. 2020).
3 Formal errors of PM estimates
Here, we compare formal errors of sub-daily PM estimates. The formal errors of the sub-daily pole coordinates are derived from the variance–covariance matrix as the indicators of the parameter precision and independence. Moreover, the formal errors of the system-specific series, i.e., GPS, GLO, and GAL, should indicate the mutual contribution of each satellite constellation to the combined solution (GRE). The general statistics of the formal errors for the X and Y components are summarized in Table 4. The statistics for both X and Y pole coordinates roughly correspond to each other. Thus, we focus on X pole coordinate only. For the 1-day arc, the lowest standard deviation of the formal errors is obtained for the combined multi-GNSS solutions. The mean formal errors equal 22, 26, 43, 37, 31 µas, for GRE, GPS, GLO, GAL, and GAB solutions, respectively. In the case of the uncorrelated contributions of GPS, GLONASS, and Galileo, one would expect the formal errors of the combined solution at the level of 19 µas. However, we cannot say that the contributions are independent, because of the common processing and the parameters, which are estimated, e.g., station coordinates. The formal errors should reflect the contributions of the individual subsystems into the combined solution. Thus, GRE products are mostly influenced by GPS-based results because of the lowest errors.
When cross-referencing GAL and GAB solution, the mean and standard deviation of the formal errors decreases approximately by 15% and 10%, respectively. This improvement should be attributed to the reduction in the correlations between the parameters, as we decreased the number of the estimated empirical parameters of the ECOM model from 7 to 5 (Table 3).
While using 3-day arcs, we theoretically expect an observed improvement factor of the mean formal errors at the level of \( \sqrt 3 \approx 1.73 \), when compared to the 1-day arc solutions. That is because approximately three times more observations are used, whereas the number of estimated parameters increases only slightly as the most important parameters, such as station coordinates and orbits, are common for the 3-day arc solutions. The improvement in formal errors was even more prominent in the case of the GNSS-based daily ERP estimates as reported by Zajdel et al. (2020) and Lutz et al. (2016) because of the continuity of orbits and ERPs over the orbital arc as well as the decorrelation between ERPs estimated with 1-day intervals and the station coordinates and orbit parameters. However, in the analyzed case, the observed magnitude of improvement is lower than expected and equals 1.3, 1.4, 1.5, 1.6, and 1.4 for GRE, GPS, GLO, GAL, and GAB solutions, respectively. Therefore, one may say that the lengthening of the orbital arc is actually more beneficial in the case of the daily sampled parameters than for the sub-daily sampled parameters, for which the existing correlations remain.
There are two patterns of variations visible in the formal errors of PM: (1) low-frequency fluctuations with a period longer than 24 h, and (2) high-frequency variations within the 24 h band. The low-frequency variation is mostly visible for the system-specific solutions and originates from the changes in the mutual orientation of the orbital planes in the constellation (see Fig. 1). In the case of GPS, GLO, GAL, and GAB solutions, the increase in formal errors is visible when pairs of orbital planes have the same orientation with respect to the position of the Sun, i.e., the same Sun elevation angle above the orbital plane − β. The exception is a configuration when the similar low values of β for the orbital plane pairs coexist with an extreme value of β for the remaining plane. Furthermore, such a pattern is almost entirely reduced in the combined GRE series. Hence, the abundance of the GNSS constellations and observational geometries improve the theoretical separability of the estimated parameters. The characteristic patterns are also reduced in the GAB solution when compared to the GAL solution. The leading cause of the reduced pattern for the GAB solution is the reduced correlations that are β dependent (Zajdel et al. 2021). The standard deviation of formal errors decreases by about 11% comparing 1-day GAB and GAL solutions. The estimation of extra empirical orbit parameters makes the solution more prone to systematic errors in the estimated parameters if those are correlated with the other parameters in the solution. Thus, the estimation of extra periodic empirical acceleration parameters, as it is done in GAL, GLO, and GPS solutions, may subject the estimated PM to orbit-related errors, especially in the particular epochs, when the formal errors are the highest.
Time series of formal errors of the X pole coordinate from the combined multi-GNSS solution and system-specific solutions (dots). The solid line represents the median values within the moving window of 3 days. β angles for the particular orbital planes of the constellation are marked with gray lines (right axis). The colored lines refer to the 1-day solutions, while black lines refer to the corresponding 3-day solutions
Figure 2 shows the amplitude spectra of the formal errors in the band up to 24 h. For the 1-day solutions, the pronounced peaks are visible at the harmonics of 24 h, i.e., for 24, 12, 8, 6, 4.8, and 4 h. The amplitudes of the most prominent signal with a period of 24 h equal 2.3, 2.9, 8.4, 4.8, and 6.3 µas, for GRE, GPS, GLO, GAL, and GAB solutions, respectively. The signal is damped by approximately 5–6 times when the 3-day processing is applied for all the solutions.
Figure 3 illustrates formal errors for the pole coordinates estimated at the particular hours of a day. In the case of 1-day processing, the formal errors are higher for the boundary values than for the estimates in the middle of the processing window. The median of the formal errors is reduced for the estimates which are assigned to the noon when compared to the estimates from the midnight by approximately 30% for GRE, GPS, and GAL solutions and even 40% for GLO and GAB solutions. Most of the other parameters in the processing such as station coordinates or orbit initial state vectors are also best determined for the middle epochs. Moreover, in the case of the 1-day arc, the midnight estimates coincide with the boundary epoch of the arc. The edge of the arc is naturally the weakest point due to the lack of preceding or following observations. Thus, the increased formal errors for the PM estimates at the midnight epochs should also be directly attributed to both these issues. In the case of the 3-day arc solutions, the formal errors are roughly equal for all particular 2-h estimates extracted from the middle day of the arc. Thus, the strategy of using only the sub-daily estimates corresponding to the middle day of the 3-day arc stabilizes the precision of the sub-daily PM estimation, which agree well with the conclusions given by Lutz et al. (2016) for ERPs estimated with 24 h time resolution.
Formal errors of sub-daily X-pole coordinates at the particular hours of estimation. The colored whiskers refer to 1-day solutions, while black whiskers refer to the corresponding values from the middle day of the 3-day solutions. Horizontal lines refer to the median values; the error bars range from 5 to 95 percentile. The 24-h epoch has been removed because it is redundant with respect to the estimates at the 0-h epoch
4 Characteristic of GNSS-based sub-daily PM
We assess the overall quality of the particular solutions w.r.t. the reference solution. Table 5 shows differences between the estimated series of pole coordinates and the a priori series of IERS EOP-C04-14 supplemented by a sub-daily variation in PM from the model recommended in the IERS2010 conventions. For the 1-day arc solutions, systematic offsets are visible for the particular series which equal 41, 32, 97, 30, and 27 µas for GRE, GPS, GLO, GAL, and GAB solutions, respectively. We see that the GAL and GPS solutions fit better to the a priori model than the GLO solution, which is mostly responsible for the large mean offset in the combined solution. The larger offset for GLONASS-based solutions than for the other solutions may be caused by issues of the precise orbit determination (Dach et al. 2019). Another source of the offset in PM may also be found in the lack of the most up-to-date antenna calibrations for Galileo satellites and ground antennas applied in the processing. We decided not to use them because of the inconsistencies between the Galileo-based scale and IGS14 scale as reported by Villiger et al. (2020). Whether the change of this processing feature would improve or not the estimates of ERPs should be further investigated. Moreover, the systematic shifts in geocenter may cause translations in PM offset (Ray et al. 2017) because some systematic offsets are visible in the orbit origin seen by different GNSS constellations (Zajdel et al. 2019). The standard deviation of ERP residuals equals 106, 120, 207, 190, 159 µas for GRE, GPS, GLO, GAL, and GAB solutions, respectively. Thus, the combined multi-GNSS solution is the least scattered. When using 3-day arcs, the statistics do not improve significantly (Table 5). The standard deviation of PM residuals reflects both inconsistencies between the estimates and the a priori models of low- and high-frequency variations. The small differences between the metrics of 1-day and 3-day arc solutions indicate that the magnitude of agreement with the a priori models depends rather on satellite systems than the arc-length. However, a clear improvement is visible when the approach for SRP modeling is changed for Galileo satellites from the empirical ECOM2 model to the hybrid SRP approach. The improvement for the standard deviation of PM residuals reaches 17%, and 19% for X and Y coordinates, respectively, when comparing GAB to GAL solutions.
5 Non-tidal signals in GNSS-based PM
Polar motion, as observed by the geodetic techniques, can be defined as the location of the rotation axis in the direction of the Greenwich and 90° W meridians for the X and Y directions, respectively. For the frequency analysis of the PM, we decomposed the time series of both the X and Y pole coordinates to complete prograde and retrograde motion. The time series of pole coordinates can be described as a Fourier series:
where \( C_{k,x} \), \( C_{k,y} \), \( S_{k,x} \), \( S_{k,y} \) represent the amplitudes for cosine and sine terms of the \( k \) element for the x and y pole coordinates. In the case of the tidally driven variations in PM, the angular variable \( \varphi_{k(t)} \) denotes the astronomical fundamental argument for the \( k \) tide at the epoch \( t \) (Petit and Luzum 2010). \( X_{p} \) and \( Y_{p} \) are the estimated X and Y pole coordinates, respectively. Then, based on the Fourier coefficients of pole coordinates, prograde and retrograde amplitudes and phases of PM can be determined as:
where \( p(t) \) denotes PM and \( A_{\text{pro}} , \phi_{\text{pro}} , A_{\text{retro}} ,\phi_{\text{retro}} \) are the amplitude and phase components for the prograde and retrograde parts, respectively.
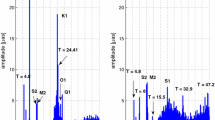
Figure 4 illustrates the spectra of PM differences w.r.t. the model recommended by the IERS 2010 Conventions in prograde and retrograde directions based on the 1-day arc solutions. We evaluated the overall level of the variability of the particular solutions using the root mean square (RMS) of the amplitudes in the frequency domain. According to Parseval’s theorem (Buttkus 2000), the total energy of the signal is preserved in both time and frequency domains. The RMS for the PM spectra up to 48-h periods is at the level of 1.2, 1.5, 2.5, and 2.4 µas in prograde and 1.0, 1.2, 2.2, 1.8 µas in retrograde for GRE, GPS, GLO, and GAL solutions, respectively. Therefore, we may consider the amplitudes above this level as meaningful. The largest discrepancies for PM occur in the diurnal and semi-diurnal bands close to the tidal constituents. The evaluation of the consistency between each series at the tidal frequencies is conducted in Sect. 8. The peaks in the retrograde diurnal PM spectrum are artifacts, which may originate from both imperfections in the numerical filter on blocking retrograde diurnal motion (Hefty et al. 2000; Thaller et al. 2007) and aliasing of the errors in the a priori nutation model, which has been used in the processing (Table 2). The residual signal at diurnal retrograde frequency equals 5.3, 6.3, 11.7, 7.2 µas for GRE, GPS, GLO, and GAL solutions, respectively. Thus, the signal for GLONASS is almost two times larger than for the other constellations.
Amplitude spectra of PM residuals w.r.t. the IERS2010 sub-daily model, decomposed into prograde (a) and retrograde (b) parts for GAL, GLO, GPS, and GRE 1-day arc solutions. The cyan vertical lines mark the theoretical orbital periods. The orange vertical lines mark the main tidal periods. The magenta vertical lines mark the harmonics of 24 h
Moreover, some artificial signals are visible at the frequencies which are not related to any tidal terms. The estimation of sub-daily ERPs using GNSS is limited as the variations in Earth rotation are observed by the dynamic system of satellites, which also rotates in conjunction with the Earth. Therefore, we may expect spurious signals at the frequencies which stem from the combination of both the frequency of Earth revolution (sidereal day) and the revolution period of the constellations (11 h 58 min for GPS, 11 h 16 min for GLONASS, and 14 h 05 min for Galileo, see Table 1). This dependency shall be described as follows:
where \( P_{o} \) is a period for which we may expect the orbit-related artificial signal. We call it orbital periods in the next parts of this article. \( f_{S} , f_{E} \) are the frequencies of the Earth revolution and the revolution period of the particular satellite constellation, respectively, whereas \( n,m \) are small integer numbers. Tables 12, 13, and 14 from “Appendix” provide a list of the most important periods which alias with GPS, GLONASS, and Galileo solutions and thus may be expected in the series of GNSS-based geodetic parameters.
Figure 4 shows the spectra of the prograde and retrograde parts of the PM separately. The theoretical orbital periods are marked for particular solutions using vertical, cyan lines. At first sight, we may clearly notice that theoretical expectations are met quite well for all the considered solutions. Three groups of spurious signals can be distinguished: (1) the signals at the harmonics of satellite revolution period (m = 0), (2) the signals at the harmonics of the Earth revolution period (n = 0), and (3) the signals at the combined frequencies of both aforementioned periods (n and m ≠ 0). The second group of periods is also close to the harmonics of 24 h.
In the first group, the amplitudes in prograde motion for both GAL and GLO solutions reach approximately 7 and 5 µas at the first and second harmonic of the satellite revolution period, respectively. The corresponding signal is also visible in the retrograde direction. None of these signals is visible in the combined multi-GNSS solution.
The second group comprises the signals which manifest at the periods that are close to the harmonics of 24 h, i.e., 4.0, 4.8, 6, 8, 12, and 24 h. Sibois et al. (2017) assigned these artifacts to the discontinuities between daily solutions. However, some parts of differences at the periods of 6, 8, 12, and 24 h could be explained by atmospheric tides and non-tidal atmosphere (AAM), dynamic ocean (OAM), and continental hydrosphere (HAM) angular momenta. The IERS2010 model contains only the effects of ocean tides and libration, whereas space geodetic techniques measure the sum of motions which may induce variations in PM. Moreover, it is also of paramount importance that the tidal displacements affect the GNSS tracking network, which may also manifest as the residual signals. The signal is visible in both prograde and retrograde parts, for each system-specific solution. However, all the amplitudes significantly decrease in the combined multi-GNSS solution. Therefore, one may conclude that this artifact is inherent to the single-constellation GNSS processing. In the GRE solution, the amplitudes equal 7.9, 5.1, 3.2 µas in prograde and 3.9, 3.9, 5.6 µas in retrograde at the periods of 4.8, 6, and 8 h, respectively. The amplitude at the frequency of 4.8 h is the most pronounced non-tidal signal in the GPS series. Because of the high impact of the GPS on the combined solution, the signal of 4.8 h is also clearly visible in the amplitude spectrum of the GRE solution. The 6-h period corresponds to S4 tide; however, the amplitude, which is visible in the GNSS seems to be largely overestimated, and further investigations are required to evaluate its theoretical power. The amplitude of the S3 (8-h period) spectral line can be explained by the atmospheric tide with thermal origin (Brzeziński et al. 2002; Sibois et al. 2017), which may justify the amplitudes of 0.46 and 0.57 µas in prograde and retrograde directions, respectively (de Viron et al. 2005). However, the observed amplitude is still approximately three times larger than theoretically considered by de Viron et al. (2005). The residual amplitudes at the diurnal and semi-diurnal bands will be extensively analyzed in the next sections.
The third group is formed by the cluster of signals with no geophysical interpretation, as they arise from the resonance between the Earth rotation period and satellite revolution period. The most pronounced peaks are visible for the periods, which arise from Eq. 8 with a ratio of n = 1 and m = − 1. The period equals ~ 34 h, ~ 21 h, and ~ 24 h for the Galileo, GLONASS, and GPS constellation, respectively. The amplitudes of these signals equal approximately 30 and 21 µas, for GAL and GLO solutions, respectively. In the case of the GPS constellation, it is difficult to extract this effect because the orbital period lines up with the K1 tide. Thus, one can conclude that the estimation of K1 tide, as well as the other tidal terms in the diurnal band, is somehow affected by the exact 2:1 resonance between the GPS revolution period and Earth rotation. The reader is referred to “Appendix” section to investigate a full range of theoretical orbital periods, which can be calculated for the particular satellite systems in different configurations of n and m variables in the range between − 9 and 9. To give an impression on the magnitude of this effect, for the GAL solution the amplitudes at the most pronounced peaks amount to 11.2 µas at − 8.87 h, 8.7 µas at − 14.95 h, 5.2 µas at 8.87 h, 4.4 µas at 4.35 h, and 4.0 µas at 7.72 h. For GLO solution, the peaks are considerably higher and reach the amplitude of 16.3 µas at − 4.56 h, 12.1 µas at − 7.66 h, 8.1 at − 5.32 h, 21.3 µas at 7.37 h, 10.7 µas at 19.17 h, 7.2 µas at 10.64 h.
As opposed to the particular system-specific solutions, the combined solution is not affected by most of the system-specific orbital periods. Except for the periods at the harmonics of 24 h, only three orbital peaks can be distinguished for the GRE solution. The amplitudes are 6.7, 4.8, and 4.7 µas at the periods of 7.37 h, − 7.66 h, and − 4.56 h, respectively. Apparently, all of them originate from the GLONASS orbital periods. The spurious amplitudes at the orbital periods are generally larger for the GLO solution than for the GAL solution. This might be related to GLONASS-specific problems such as inter-frequency biases or the difficulties in ambiguity fixing for GLONASS (Teunissen and Khodabandeh 2019). Moreover, the Galileo constellation consists not only of nominal satellites with a revolution period of 14 h 05 min but also of two satellites on the highly eccentric orbits with a shortened revolution period of ~ 12 h 56 min (see Table 1). Conceivably, the same as for the GRE solution, a combination of satellites with different orbital characteristics may diminish the impact of orbital periods.
6 Impact of SRP modeling on sub-daily PM estimates
Figure 5 shows the comparison of the spectra of PM for two Galileo-only solutions, which differ in the SRP modeling (Table 3). The occurrence of non-tidal orbital signals described in the previous section is independent of the changes in the SRP modeling. All three groups of signals are visible in the frequency domain of the PM. The spurious peak at the orbital period of ~ 34 h is still dominant, while the decrease in the amplitude is at the negligible level of few µas, which may correspond with a decrease in the noise floor, especially for the prograde part for periods longer than 19 h. When comparing GAB to GAL solutions, the RMS of the noise floor decreased by approximately 33% for the amplitudes at the periods between 19 and 48 h in the prograde part. Consequently, the amplitudes of the signals are sharper for GAB, especially for the diurnal tidal band. More noise floor and energy are visible in the diurnal band for the GAL solution; thus, it stresses the challenging aspect of the recovery of diurnal tidal signals in this solution. The improvement for the other spurious peaks at different orbital periods is at the level below 10%. Interestingly, the amplitudes of the peaks at the harmonics of 24 h, i.e., 4, 4.8, 6, and 8 h could be reduced by approximately 15% and 30% for the prograde and retrograde part, respectively, if there are no periodic ECOM parameters estimated in the solution. However, because of the other issues found in the estimated orbital parameters, geocenter coordinates, and daily ERPs in a processing strategy without any periodic ECOM parameters, we excluded this test case from the analyses (Bury et al. 2019; Zajdel et al. 2020). Nevertheless, one can conclude that the reduction in the empirical periodic terms in the orbit model improves the amplitudes of the spurious signals at the harmonics of 24 h. Thus, deficiencies in the SRP modeling contribute not only to the spurious signals at the orbit-harmonic frequencies but also to the daily signals. The GAB-like box-wing model, which is uniform in quality for the whole constellation, can be constructed for Galileo. In the case of the remaining GNSS constellations, there is only a limited set of the official and detailed metadata for the different types of satellites. However, we might expect a similar kind of improvement when using satellite metadata for the particular satellites (Fliegel and Gallini 1996) and complete this set with the approximated or estimated properties of satellites as proposed by Rodriguez-Solano et al. (2014).
Amplitude spectra of PM residuals w.r.t. the IERS2010 sub-daily model, decomposed into prograde (a) and retrograde (b) parts for GAL, GAB 1-day arc solutions. The cyan vertical lines mark the theoretical orbital periods. The orange vertical lines mark the main tidal periods. The magenta vertical lines mark the harmonics of 24 h
7 Impact of the arc-length on sub-daily PM estimates
To gain insight into some of the potential error sources or systematic effects affecting the solutions, we have also compared the sub-daily PM delivered from 1-day and 3-day processing. The 1-day processing window of GNSS solutions couples with the Earth rotation period. This may potentially affect both tidal and non-tidal signals in the sub-daily estimates of PM. Lutz et al. (2016) explicitly recognized that the quality of PM rates increases dramatically when comparing 1-day with 3-day solutions. Figure 6 illustrates the comparison between the spectra of PM for 1-day and 3-day solutions for the GAB, GAL, GLO, GPS, and GRE solutions. An interesting feature that emerges from this comparison is that the change in the solution length only marginally affects the amplitudes at the periods of the 24 h harmonics. However, this is not in line with the findings given by Sibois et al. (2017). The residual signals at diurnal retrograde frequency decreased by a factor of two between 3-day and 1-day solutions; however, these signals are still visible in the results above the level of the noise floor. The improvement in the noise floor is visible for the GAB, GAL, and GLO solutions, while in the case of the GPS solution, the change in the solution length has an imperceptible impact on the results. For the GAB, GAL, and GLO solutions, there are more non-tidal signals visible in the 1-day solutions than in the corresponding 3-day solution. The amplitude for most of the orbital periods decreased almost to the level of the noise floor for the GLO and GPS solutions. On the other hand, the amplitudes for the most pronounced orbital periods, which are listed in Sect. 5, decreased by approximately 20–30%. It means that non-tidal signals, which are visible in the frequency domain at the orbital periods, depend on the combination of (1) the revolution period of particular satellite constellation, (2) rotation period of the Earth, and (3) the length of the orbital arc.
8 Variations in tidal coefficients
The frequencies to be expected in the sub-daily ERPs are induced by tides; thus, they are known from theory. As there are hundreds of tidal frequencies and it is neither practical nor mathematically feasible to comprise all the possible constituents in the analysis, it is essential to choose the set of tidal terms which can be fitted into the considered dataset. With a time series of 3 years, it is inappropriate to include in the harmonic analysis all 71 tidal terms, which have been considered in the IERS2010 model. The short time range and close frequencies of the estimated tidal terms may result in an ill-conditioned normal equation system. Thus, only 38 main tidal terms have been chosen, including 25 diurnal and 13 semi-diurnal terms. According to the Rayleigh’s criteria (Gipson 1996; Godin 1972), 3 years of data is sufficient to determine the tidal constituents which differ by 78.8 s in a diurnal band and 19.7 s in a semi-diurnal band (Thaller et al. 2007).
The tidally driven variations in PM can be described using Eqs. 1 and 2. Then, we estimate Cx, Cy, Sx, Sy in constrained least squares adjustment using the pole coordinate estimates as observations weighted by their formal errors. Additionally, we removed the offset and drift for both PM components over the entire series to eliminate the systematic errors in the results of estimation (Rothacher et al. 2001). As previously mentioned, the sub-daily PM was estimated w.r.t. the a priori sub-daily model. Thus, the model values had to be reapplied to the series. As demonstrated in the previous sections, the results, which come from the 3-day arc solutions are slightly better compared to the 1-day arc results. Thus, we decided to limit the discussion in this section to the 3-day arc results only.
To properly estimate the coefficients of the major tidal terms, we constrain the ratio of the coefficients of the sideband terms and the terms of the major tides according to Gipson (1996) and Rothacher et al. (2001). Hence, eight additional tides can be estimated: Q1′, O1′, K1′, K1″, OO1′, υ1′, M2′, K2′ compared to the set of 30 main tides. Because of the conventional distinction between PM and nutation, we should not expect any signal in the retrograde PM. However, as it is pointed out in Sect. 7, some of the residual signals appear in the considered series. In an aim to remove the spurious contribution of retrograde diurnal PM, additional constraints had to be added to the normal equation system for the 25 diurnal tidal terms using Eq. 9.
The estimation method of least squares allows precision estimation of the adjusted quantities. The sum of the squares of the residuals divided by the degrees of freedom is at the level of 6, 5, 6, 7, 6 µas for GRE, GPS, GLO, GAL and GAB solutions, respectively. The formal errors of the adjusted quantities of the sine and cosine coefficients equal approximately 1.5 µas based on the covariance matrix as delivered in the least square adjustment. The reader is referred to “Appendix” section to investigate the estimated models, which consist of 38 tidal terms based on all the GNSS-based solutions.
Finally, we may compare the estimated empirical models with independent models. The deficiencies in the model of sub-daily variations in PM so far recommended by the IERS conventions 2010 led the scientific community to the need for the development of a new model (Artz et al. 2010; Desai and Sibois 2016). In recent years the ‘IERS Working Group on Diurnal and Subdiurnal Earth Orientation Variation’ (IERS HF-EOP WG) has been working on the potential alternative to the currently recommended model in the frame of the future efforts on the reprocessing campaigns for the next International Terrestrial Reference Frame (ITRF) realizations (Altamimi et al. 2016; Desai and Sibois 2016; Madzak et al. 2016). For the purpose of the independent validation of our GNSS-based models, we chose three, alternative models for diurnal and semi-diurnal tidal variations as described by Desai–SiboisFootnote 1 (Desai and Sibois 2016) and GipsonFootnote 2 (Gipson 2017). In the next two subsections, we provide the direct comparison of the external models as well as the conformity assessment of our results with respect to these three models.
8.1 Comparison of external models for sub-daily variations in PM
Some significant deficiencies were visible in previous sections between the estimated sub-daily ERP series and the IERS2010 model in the diurnal and semi-diurnal bands. To distinguish which part of the differences is due to the deficiencies of the reference model and which part is due to the issues of the GNSS analysis, we provide the comparison of different reference models. The model recommended in the IERS 2010 Conventions was deduced from a combination of an ocean tide forward model with the TOPEX/Poseidon satellite altimetry measurements (TPXO.2, Egbert et al. 1994). The Desai–Sibois model is based on an updated altimetry-constrained ocean tide atlas TPXO.8 (Egbert et al. 1994). As the Desai–Sibois model is a pure geophysical model based on the ocean tide atlas, it solely accounts for the variations in the Earth rotation induced by the oceans. The Gipson model is a purely empirical model based on VLBI data, which have been collected up to 2017. There are two models provided by Gipson in the frame of IERS HF-EOP WG, which vary in the way how libration is handled: (1) the model which includes the libration in the a priori model and (2) the model which does not include libration in the a priori model. We chose the model (1), which is consistent in output with our approach and the Desai–Sibois model.
The model discrepancies can be evaluated using the approach proposed by Desai and Sibois (2016). Each individual model is described by the sine and cosine coefficients of the tidal frequencies. The difference between models can be split into the differences in the amplitudes of the particular tidal lines in the prograde and retrograde direction of PM using Eqs. 4 and 6.
Figure 7 illustrates the differences between the 71 tidal components, which are common for all the three considered models. In the case of the difference between the IERS2010 and Desai–Sibois models, the RMS of differences equals 6.1, 1.5, and 2.4 µas for prograde diurnal, prograde semi-diurnal, and retrograde semi-diurnal components, respectively. On the other hand, the RMS of differences between the IERS2010 and Gipson model is 5.4, 2.5, and 4.7 µas. Most of the differences between the IERS2010 and Desai–Sibois models do not exceed 2 µas. The most significant differences are visible only for the main tidal components including the terms O1, M1, P1, K1, OO1, N2, M2, S2, and K2 terms. The largest differences equal 30.6 and 20.5, 10.0, 9.4 µas for O1 (pro.), K1 (pro.), S2 (retro.), and P1 (pro.) terms, respectively. In the case of the comparison between the IERS2010 and Gipson models, the differences are more spread over the whole set of tidal terms. Almost 80% of the presented differences exceed 1 µas. However, the differences in the main tidal terms in the Gipson model are lower than in the case of the Desai–Sibois model. The largest differences reach 24.0, 13.3, 12.6, 10.4 and 10.3 µas for O1 (pro.), M2 (retro.), S2 (retro.), K1 (pro.), and S1 (pro.), respectively. The consistency between the Desai–Siboi and Gipson models is at the level of 5.3, 2.4, and 3.8 µas for prograde diurnal, prograde semi-diurnal, and retrograde semi-diurnal components, respectively.
8.2 Comparison of the results with the external models
Figure 8 illustrates the residuals of the estimated amplitudes and phases w.r.t. the reference values from the Desai–Sibois model, for the 9 most dominant tides labeled as N2, M2, S2, K2, Q1, O1, P1, S1, and K1. We decided to use the Desai–Sibois model as the reference for this comparison in accordance with the recommendation of the IERS HF-EOP WG, whose members recommended the Desai–Sibois model for the reprocessing activities on the road to the ITRF2020Footnote 3. The GNSS-based solutions are consistent with each other as the amplitude differences are coherent up to approximately 10 µas. The calculated phases are also consistent within a few degrees. The difference in the phase lag is visible mainly for the S1 tidal term for the empirical solutions. As we demonstrated in the previous sections, each of the system-specific solutions is partly affected by the impact of the artificial signals at the orbital periods, which may lead to inconsistencies at the particular tidal lines. The combined multi-GNSS solution is most immune to the influence of system-specific spurious artifacts. Therefore, the estimated amplitudes from the GRE solution are most consistent with the reference values based on tidal models. The largest differences between the GNSS-based solutions and the Desai–Sibois model are visible for the M2, O1, S1 and K1 terms with the differences at the level of 5.2 (prograde)/3.8 (retrograde), 10, 6.8, and 14 µas, respectively. The differences at the K1 tidal term between the GRE and Desai–Sibois models are approximately two times lower compared with the IERS2010 model (Fig. 8). In the case of the O1 tidal term, the adjusted amplitudes differ by approximately 10 µas comparing to the Desai–Sibois and IERS2010 models. However, the GNSS-based results are consistent with the VLBI model (Gipson). The reason for that may be found in the inconsistency in the libration model as the same is applied a priori in all these empirical models (Desai and Sibois 2016). The differences at the level of 8–15 µas depending on the solution are also visible for the amplitudes of the S1 tidal term for all the empirical models. Most of the other parameters in the processing, such as station coordinates or orbit parameters, are calculated with a 24 h interval, which coincides with the period of the S1 tide. Moreover, several other sources, beside the ocean tides, contribute to the signal with a period of 24 h. The expected magnitude of these signals may reach 7.1, 7.8, and 17 µas for the atmospheric tides, non-tidal AAM, and non-tidal OAM, respectively (Brzeziński et al. 2004). GNSS can only measure the sum of these effects. This fact could explain the differences in the amplitude and phases between the empirical models and the geophysical/ocean-based models such as the Desai–Sibois model or the model recommended in the IERS Conventions 2010.
Figure 9 illustrates the overall consistency between the amplitudes of 38 tidal terms, which have been recovered through our adjusted tidal coefficients, and three external models of sub-daily variations in PM. Table 6 summarizes the inter-quartile ranges (IQR) of the amplitude differences as the indicator of consistency between the solutions. The IQRs of the amplitudes and the medians do not exceed 7 µas (Fig. 9). The consistency between the GNSS-based empirical models and the IERS2010 model is at the level of 3.8, 6.7, 6.5, 3.2 µas for prograde diurnal tidal terms, 1.6, 2.6, 3.3, 1.6 µas for the semi-diurnal prograde tidal terms, and 4.2, 6.8, 5.6, 4.5 for retrograde semi-diurnal tidal terms, for the combined GRE, GPS, GLO, and GAB solutions, respectively. The consistency of GPS-based diurnal tidal terms with the external models is worse than in the case of the Galileo solutions. Therefore, it may confirm the presumption that the resonance between the GPS revolution period and the Earth rotation affects the estimated diurnal tidal lines. The approximately 40% of the improvement in the consistency with external models for the prograde diurnal tidal terms is achieved for the Galileo solution when the hybrid approach for SRP modeling is applied compared to the empirical GAL solution (see Table 6). The GAB solution is fairly comparable regarding the consistency with the other models to the multi-GNSS GRE solution. However, the single-system GAB solution is still prone to the system-specific orbital periods; thus, we are inclined to the GRE solution as the best solution of today. If we take the GRE solution as the most reliable GNSS-based estimates of sub-daily PM, we may quantitatively evaluate the consistency of the GNSS-based results w.r.t. the independent models. The consistency is at the level of 1.6, 2.8, and 3.8 µas for diurnal prograde tidal terms, 1.2, 1.4, 1.6 µas for semi-diurnal prograde tidal terms, and 2.1, 2.6, and 4.2 µas for semi-diurnal retrograde tidal terms, for the Desai–Sibois, Gipson, and IERS2010 models, respectively. We see that the GNSS-based estimates are more consistent with the Gipson and Desai–Sibois models than with the IERS2010 model. This statement is also in line with the current recommendations of the IERS HF-EOP WG for using the Desai–Sibois model instead of the model so far recommended in the IERS 2010 Conventions.
9 Conclusions
The GNSS technique is sensitive to the sub-daily variations in PM and can be used for the recovery of the pole coordinates with a sub-daily resolution. Nonetheless, we see non-trivial differences between the PM estimates, delivered by different GNSS constellations including GPS, GLONASS, Galileo, and the combined multi-GNSS solutions. For the first time, the system-specific signals in the sub-daily PM from Galileo have been described. The overall consistency between the individual GNSS-based solutions w.r.t. the reference series PM variations is at the level of 100, 110, 160, 135 µas for GRE, GPS, GLO, GAB solutions, respectively. The increased level of the standard deviation for the GLONASS-only and Galileo-only solutions can be justified by (1) the imperfections in SRP modeling for GLONASS and Galileo satellites, (2) influence of the non-tidal signals which seem to be inherent for the GNSS-based system-specific solutions, (3) other system-specific issues including, e.g., the lack of precise antenna phase center offsets and variations for Galileo frequencies applied in the processing, inter-frequency biases or the difficulties in ambiguity fixing for GLONASS (Teunissen and Khodabandeh 2019), and the number of orbital planes, which results in the different impact of β-dependent orbit modeling issues affecting the other estimated parameters (Scaramuzza et al. 2018).
Three groups of spurious signals can be distinguished: (1) the signals at the harmonics of satellite revolution periods, (2) the signals at the harmonics of the Earth rotation period, and (3) the signals at the combined frequencies of both aforementioned periods. We called this group of non-tidal signals as orbital periods.
First, we found that the pronounced peaks are visible at the harmonics of 24 h, i.e., 24, 12, 8, 6, 4.8, 4 h. The GNSS technique measures the sum of the effects caused by the oceans and those coming from other sources, which are not modeled in the processing, i.e., atmospheric tides (S1, S2, S3, S4 tidal terms), non-tidal AAM and OAM (S1 tidal term). However, the observed amplitudes are approximately three times larger than it could be expected from theory (Brzeziński et al. 2002; de Viron et al. 2005). This aspect needs thus further investigations. We also found that the amplitudes of the peaks at the harmonics of 24 h would have been weakened if we could reduce the number of estimated periodic parameters in the orbit model. Despite the development of the analytical models of the satellites, the estimation of the empirical periodic terms in the orbit model seems to be still irresistible and a further improvement in the orbit model based on the metadata is required.
Moreover, we identified that we can expect strong spurious signals at the periods of ~ 34 h, ~ 21 h, 24 h for the Galileo, GLONASS, and GPS, respectively, because of the combination of the satellite revolution periods and the Earth rotation period. The amplitudes of these signals equal approximately 30 and 21 µas, for GAL and GLO solutions, respectively. In the case of the GPS constellation, it is difficult to extract the quantitative impact of this effect as the GPS orbital period lines up with the K1 tide. Thus, one can conclude that the estimation of K1 tide, as well as the other tidal terms in the diurnal band, is directly affected in the GPS-based solution.
On the other hand, the estimates of sub-daily PM are also influenced by the arc-length of the orbit. If we extend the standard 24 h orbit arc to 72 h, the amplitudes for the most pronounced orbital periods for GLO and GAL solution decrease by approximately 20–30%. It means that non-tidal signals, which are visible in the frequency domain at the orbital periods, depend on the combination of (1) the revolution period of the particular satellite constellation, (2) rotational period of the Earth, and (3) the length of the orbit arc.
As opposed to the particular system-specific solutions, the combined solution is not affected by most of the system-specific orbital periods. Thus, we claim that the processing of the combined multi-GNSS observations is beneficial for the estimation of sub-daily PM.
We showed that the improved SRP modeling for Galileo satellites, which comprises the box-wing model, can reduce the impact of the particular non-tidal signals even by 30%. Moreover, the level of the noise floor of the amplitudes in the diurnal frequency band can be reduced by the factor of two when cross-referencing GAB and GAL solutions. The multi-GNSS solution incorporating the detailed box-wing models for GPS, GLONASS, and Galileo satellites would lead to even better results than the current GRE solution. Furthermore, the time series of sub-daily PM may contribute to the validation of GNSS orbit models, as the change in SRP modeling highly influences the signal and the noise floor level in the high-frequency ERP estimates.
Finally, we adjusted the sine and cosine coefficients for 38 tidal frequencies based on the sub-daily PM estimates. We assessed that the GNSS-based results are in overall consistent with the model proposed by Desai–Sibois to the level of a few µas. The Desai–Sibois model is also more consistent with GNSS results for the main tidal terms than the currently recommended model in the IERS 2010 Conventions. The results which are delivered by different GNSS constellations are also consistent with each other at the level of a few µas, especially in the prograde part. The GNSS-based empirical sub-daily PM models may contribute to the evaluation of the other models. On the other hand, further studies have to be carried out to evaluate the impact of the a priori model of sub-daily variations in PM change on the other parameters, which are estimated in the multi-GNSS processing, including orbits, daily ERPs, and station coordinates. Similar consideration has been done by Panafidina et al. (2019) based on the artificial amplification imposed on the K1 tidal term.
The appendices contain the complete empirical sub-daily PM models based on GPS, GLONASS, Galileo employing empirical and hybrid orbit models, and the combined multi-GNSS solution.
References
Abraha KE, Teferle FN, Hunegaw A, Dach R (2018) Effects of unmodelled tidal displacements in GPS and GLONASS coordinate time-series. Geophys J Int 214(3):2195–2206. https://doi.org/10.1093/gji/ggy254
Altamimi Z, Rebischung P, Métivier L, Collilieux X (2016) ITRF2014: a new release of the International Terrestrial Reference Frame modeling nonlinear station motions. J Geophys Res Solid Earth 121(8):6109–6131. https://doi.org/10.1002/2016JB013098
Arnold D, Meindl M, Beutler G, Dach R, Schaer S, Lutz S, Prange L, Sośnica K, Mervart L, Jäggi A (2015) CODE’s new solar radiation pressure model for GNSS orbit determination. J Geod 89:775–791. https://doi.org/10.1007/s00190-015-0814-4
Artz T, Böckmann S, Nothnagel A, Steigenberger P (2010) Subdiurnal variations in the Earth’s rotation from continuous Very Long Baseline Interferometry campaigns. J Geod Res 115(B5):B05404. https://doi.org/10.1029/2009JB006834
Artz T, Bernhard L, Nothnagel A, Steigenberger P, Tesmer S (2012) Methodology for the combination of sub-daily Earth rotation from GPS and VLBI observations. J Geod 86(3):221–239. https://doi.org/10.1007/s00190-011-0512-9
Beutler G, Brockmann E, Gurtner W, Hugentobler U, Mervart L, Rothacher M (1994) Extended orbit modeling techniques at the CODE processing center of the international GPS service for geodynamics (IGS): theory and initial results. Manuscr Geod 19:367–386
Bizouard C, Seoane L (2010) Atmospheric and oceanic forcing of the rapid polar motion. J Geod 84:19–30. https://doi.org/10.1007/s00190-009-0341-2
Bizouard C, Lambert S, Gattano C, Becker O, Richard J-Y (2018) The IERS EOP 14C04 solution for Earth orientation parameters consistent with ITRF 2014. J Geod 93:621–633. https://doi.org/10.1007/s00190-018-1186-3
Böhm S, Nilsson T, Schindelegger M, Schuh H (2012) High-frequency signals of oceans and atmosphere in Earth rotation. EGU General Assembly 2012, 22–27 April, Vienna, Austria
Brzeziński A, Bizouard C, Petrov SD (2002) Influence Of the atmosphere on earth rotation: what new can be learned from the recent atmospheric angular momentum estimates? Surv in Geophys 23(1):33–69. https://doi.org/10.1023/A:1014847319391
Brzeziński A, Ponte RM, Ali AH (2004) Non-tidal oceanic excitation of nutation and diurnal/semi-diurnal polar motion revisited. J Geophys Res Solid Earth. https://doi.org/10.1029/2004JB003054
Bury G, Zajdel R, Sośnica K (2019) Accounting for perturbing forces acting on Galileo using a box-wing model. GPS Solut 23(3):74. https://doi.org/10.1007/s10291-019-0860-0
Bury G, Sośnica K, Zajdel R (2020) Toward the 1-cm Galileo orbits: challenges in modeling of perturbing forces. J Geod 94:16. https://doi.org/10.1007/s00190-020-01342-2
Buttkus B (2000) Spectral representation of nonperiodic processes. In: Buttkus B (ed) Spectral analysis and filter theory in applied geophysics. Springer, Berlin, pp 13–40. https://doi.org/10.1007/978-3-642-57016-2_3
Dach R, Fridez P, Lutz S, Walser P (2015) Bernese GNSS Software version 5.2. https://doi.org/10.7892/boris.72297
Dach R, Sušnik A, Grahsl A, Villiger A, Schaer S, Arnold D, Prange L, Jäggi A (2019) Improving GLONASS orbit quality by re-estimating satellite antenna offsets. Adv Space Res 63(12):3835–3847. https://doi.org/10.1016/J.ASR.2019.02.031
de Viron O, Schwarzbaum G, Lott F, Dehant V (2005) Diurnal and subdiurnal effects of the atmosphere on the Earth rotation and geocenter motion. J Geophys Res Solid Earth. https://doi.org/10.1029/2005JB003761
Desai SD, Sibois AE (2016) Evaluating predicted diurnal and semi-diurnal tidal variations in polar motion with GPS-based observations. J Geophys Res Solid Earth 121(7):5237–5256. https://doi.org/10.1002/2016JB013125
Dilssner F, Springer T, Gienger G, Dow J (2011) The GLONASS-M satellite yaw-attitude model. Adv Space Res 47:160–171. https://doi.org/10.1016/j.asr.2010.09.007
Egbert GD, Bennett AF, Foreman MGG (1994) TOPEX/POSEIDON tides estimated using a global inverse model. J Geophys Res 99(C12):24821. https://doi.org/10.1029/94JC01894
Fliegel HF, Gallini TE (1996) Solar force modeling of block IIR Global Positioning Satellites. J Spacecraft Rockets 33:863–866. https://doi.org/10.2514/3.26851
Gipson JM (1996) Very long baseline interferometry determination of neglected tidal terms in high-frequency Earth orientation variation. J Geophys Res Solid Earth 101(B12):28051–28064. https://doi.org/10.1029/96JB02292
Gipson JM (2017) Ad hoc working group on HF-EOP Memo. https://ivscc.gsfc.nasa.gov/hfeop_wg/memos/HF_EOP_models_v2017Dec03.pdf. Accessed 12 Oct 2020
Godin G (1972) The analysis of tides. University of Toronto Press, Toronto
Griffiths J, Ray JR (2013) Sub-daily alias and draconitic errors in the IGS orbits. GPS Solut 17(3):413–422. https://doi.org/10.1007/s10291-012-0289-1
Gross RS, Fukumori I, Menemenlis D (2003) Atmospheric and oceanic excitation of the Earth’s wobbles during 1980–2000. J Geophys Res 108(B8):2370. https://doi.org/10.1029/2002JB002143
GSA (2017) Galileo satellite metadata. https://www.gsc-europa.eu/support-to-developers/galileo-satellite-metadata. Accessed 12 Oct 2020
Haas R, Wünsch J (2006) Sub-diurnal earth rotation variations from the VLBI CONT02 campaign. J Geodyn 41(1–3):94–99. https://doi.org/10.1016/J.JOG.2005.08.025
Hadas T, Kazmierski K, Sośnica K (2019) Performance of Galileo-only dual-frequency absolute positioning using the fully serviceable Galileo constellation. GPS Solut 23(4):108. https://doi.org/10.1007/s10291-019-0900-9
Hefty J, Rothacher M, Springer T, Weber R, Beutler G (2000) Analysis of the first year of Earth rotation parameters with a sub-daily resolution gained at the CODE processing center of the IGS. J Geod 74(6):479–487. https://doi.org/10.1007/s001900000108
Johnston G, Riddell A, Hausler G (2017) The International GNSS Service. In: Springer handbook of global navigation satellite systems. Springer, Cham, pp 967–982. https://doi.org/10.1007/978-3-319-42928-1_33
King MA, Watson CS, Penna NT, Clarke PJ (2008) Subdaily signals in GPS observations and their effect at semiannual and annual periods. Geophys Res Lett 35(3):L03302. https://doi.org/10.1029/2007GL032252
Kouba J (2009) A simplified yaw-attitude model for eclipsing GPS satellites. GPS Solut 13:1–12. https://doi.org/10.1007/s10291-008-0092-1
Lutz S, Meindl M, Steigenberger P, Beutler G, Sośnica K, Schaer S, Dach D, Arnold D, Thaller D, Jäggi A (2016) Impact of the arc length on GNSS analysis results. J Geod 90(4):365–378. https://doi.org/10.1007/s00190-015-0878-1
Lyard F, Lefevre F, Letellier T, Francis O (2006) Modelling the global ocean tides: modern insights from FES2004. Ocean Dyn 56:394–415. https://doi.org/10.1007/s10236-006-0086-x
Madzak M, Schindelegger M, Böhm J, Bosch W, Hagedoorn J (2016) High-frequency Earth rotation variations deduced from altimetry-based ocean tides. J Geod 90(11):1237–1253. https://doi.org/10.1007/s00190-016-0919-4
Mathews PM, Bretagnon P (2003) Polar motions equivalent to high frequency nutations for a nonrigid Earth with anelastic mantle. Astron Astrophys 400(3):1113–1128. https://doi.org/10.1051/0004-6361:20021795
Mathews PM, Herring TA, Buffett BA (2002) Modeling of nutation and precession: new nutation series for nonrigid Earth and insights into the Earth’s interior. J Geophys Res Solid Earth 107(B4):ETG 3-1–ETG 3-26. https://doi.org/10.1029/2001JB000390
Meindl M (2011) Combined analysis of observations from different global navigation satellite systems. PhD thesis. University of Bern, Bern. Geodätisch-geophysikalische Arbeiten in der Schweizm vol. 83, Schweizerische Geodätische Kommission
Meindl M, Beutler G, Thaller D, Dach R, Jäggi A (2013) Geocenter coordinates estimated from GNSS data as viewed by perturbation theory. Adv Space Res 51:1047–1064. https://doi.org/10.1016/j.asr.2012.10.026
Montenbruck O et al (2017) The multi-GNSS experiment (MGEX) of the international GNSS service (IGS)—achievements, prospects and challenges. Adv Space Res 59(7):1671–1697. https://doi.org/10.1016/J.ASR.2017.01.011
Noll CE (2010) The crustal dynamics data information system: a resource to support scientific analysis using space geodesy. Adv Space Res 45(12):1421–1440. https://doi.org/10.1016/J.ASR.2010.01.018
Panafidina N, Hugentobler U, Seitz M (2019) Influence of subdaily model for polar motion on the estimated GPS satellite orbits. J Geod 93:229–240. https://doi.org/10.1007/s00190-018-1153-z
Petit G, Luzum B (2010) IERS Technical Note No. 36—IERS Conventions (2010). Frankfurt am Main. https://www.iers.org/IERS/EN/Publications/TechnicalNotes/tn36.html. Accessed 12 Oct 2020
Prange L, Orliac E, Dach R, Arnold D, Beutler G, Schaer S, Jäggi A (2017) CODE’s five-system orbit and clock solution—the challenges of multi-GNSS data analysis. J Geod 91(4):345–360. https://doi.org/10.1007/s00190-016-0968-8
Ray RD, Steinberg DJ, Chao BF, Cartwright DE (1994) Diurnal and semi-diurnal variations in the Earth’s rotation rate induced by oceanic tides. Science (New York, N.Y.) 264(5160):830–832. https://doi.org/10.1126/science.264.5160.830
Ray J, Rebischung P, Griffiths J (2017) IGS polar motion measurement accuracy. Geod Geodyn 8(6):413–420. https://doi.org/10.1016/J.GEOG.2017.01.008
Rebischung P, Schmid R (2016) IGS14/igs14.atx: a new framework for the IGS Products. American geophysical union fall meeting 2016, abstract nr G41A-0998, 12–16 December 2016, San Francisco, USA
Rodriguez-Solano CJ, Hugentobler U, Steigenberger P, Lutz S (2012) Impact of earth radiation pressure on GPS position estimates. J Geod 86:309–317. https://doi.org/10.1007/s00190-011-0517-4
Rodriguez-Solano CJ, Hugentobler U, Steigenberger P, Bloßfeld M, Fritsche M (2014) Reducing the draconitic errors in GNSS geodetic products. J Geod 88(6):559–574. https://doi.org/10.1007/s00190-014-0704-1
Rothacher M, Beutler G, Weber R, Hefty J (2001) High-frequency variations in Earth rotation from Global Positioning System data. J Geophys Res Solid Earth 106(B7):13711–13738. https://doi.org/10.1029/2000JB900393
Scaramuzza S, Dach R, Beutler G, Arnold D, Sušnik A, Jäggi A (2018) Dependency of geodynamic parameters on the GNSS constellation. J Geod 92(1):93–104. https://doi.org/10.1007/s00190-017-1047-5
Sibois A (2011) GPS-based sub-hourly polar motion estimates: strategies and applications. University of Colorado, Boulder
Sibois AE, Desai SD, Bertiger W, Haines BJ (2017) Analysis of decade-long time series of GPS-based polar motion estimates at 15-min temporal resolution. J Geod 91(8):965–983. https://doi.org/10.1007/s00190-017-1001-6
Steigenberger P, Rothacher M, Dietrich R, Fritsche M, Rülke A, Vey S (2006) Reprocessing of a global GPS network. J Geophys Res Solid Earth. https://doi.org/10.1029/2005JB003747
Steigenberger P, Fritsche M, Dach R, Schmid R, Montenbruck O, Uhlemann M, Prange L (2016) Estimation of satellite antenna phase center offsets for Galileo. J Geod 90:773–785. https://doi.org/10.1007/s00190-016-0909-6
Teunissen PJG, Khodabandeh A (2019) GLONASS ambiguity resolution. GPS Solut. https://doi.org/10.1007/s10291-019-0890-7
Thaller D, Krügel M, Rothacher M, Tesmer V, Schmid R, Angermann D (2007) Combined Earth orientation parameters based on homogeneous and continuous VLBI and GPS data. J Geod 81(6–8):529–541. https://doi.org/10.1007/s00190-006-0115-z
Villiger A, Dach R, Schaer S, Prange L, Zimmermann F, Kuhlmann H, Wübbena G, Schmitz M, Beutler G, Jäggi A (2020) GNSS scale determination using calibrated receiver and Galileo satellite antenna patterns. J Geod 94:93. https://doi.org/10.1007/s00190-020-01417-0
Watkins MM, Eanes RJ (1994) Diurnal and semi-diurnal variations in Earth orientation determined from LAGEOS laser ranging. J Geophys Res Solid Earth 99(B9):18073–18079. https://doi.org/10.1029/94JB00805
Wei E, Jin S, Wan L, Liu W, Yang Y, Hu Z (2015) High frequency variations of Earth rotation parameters from GPS and GLONASS observations. Sensors 15(2):2944–2963. https://doi.org/10.3390/s150202944
Zajdel R, Sośnica K, Dach R, Bury G, Prange L, Jäggi A (2019) Network effects and handling of the geocenter motion in multi-GNSS processing. J Geophys Res Solid Earth 124(6):5970–5989. https://doi.org/10.1029/2019jb017443
Zajdel R, Sośnica K, Bury G, Dach R, Prange L (2020) System-specific systematic errors in earth rotation parameters derived from GPS, GLONASS, and Galileo. GPS Solut 24:74. https://doi.org/10.1007/s10291-020-00989-w
Zajdel R, Sośnica K, Bury G (2021) Geocenter coordinates derived from multi-GNSS: a look into the role of solar radiation pressure modeling. GPS Solut 25:1. https://doi.org/10.1007/s10291-020-01037-3
Acknowledgements
The International GNSS Service (Johnston et al. 2017) is acknowledged for providing multi-GNSS data. The International Earth Rotation and Reference Systems Service Working Group on Diurnal and Semi-diurnal EOP Variations is acknowledged for providing models of sub-daily Earth Orientation Parameters for comparisons and open source software to properly handle the models. The GNSS observations have been obtained from the Crustal Dynamics Data Information System (Noll 2010). Finally, we thank Prof. Urs Hugentobler and the anonymous reviewers for the thorough review and constructive comments that led to the manuscript's improved quality.
Funding
R. Zajdel, K. Sośnica, and G. Bury are supported by the Polish National Science Centre (NCN), Grant UMO-2018/29/B/ST10/00382. K. Kazmierski and G. Bury are supported by the Foundation for Polish Science (FNP).
Author information
Authors and Affiliations
Contributions
All the authors contributed to the design of the study. RZ and KS came up with the idea of the study. RZ carried out the experiments and drafted the manuscript. GB and KK performed some of the experimental analyses. RD and LP provided additional implementations to the Bernese GNSS Software. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no competing interests.
Appendix
Appendix
See Tables 7, 8, 9, 10, 11, 12, 13 and 14.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zajdel, R., Sośnica, K., Bury, G. et al. Sub-daily polar motion from GPS, GLONASS, and Galileo. J Geod 95, 3 (2021). https://doi.org/10.1007/s00190-020-01453-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00190-020-01453-w