1 Introduction

The races toward autonomous driving are stimulating innovations in high-precision global navigation satellite system (GNSS). European GNSS Agency (2017) projected a rapid growth of requirement for decimeter-level or better positioning accuracy by autonomous driving. They further stressed that, due to stringent safety standards, in all scenarios which implicate “anywhere, anytime and under any condition” does autonomous driving demand “100% position availability at decimeter level or less”. While this goal is only achievable through fusions of varieties of navigation devices and techniques, GNSS among them plays a unique and indispensable role in providing absolute positions referenced to a global coordinate frame. Due to the great and serious safety concern on self-driving vehicles, the strictest rules of navigating them, such as instantaneous decimeter- or even centimeter-level positioning, should be imposed to assure consumers of the vehicle manufacturers’ safety commitments.

Instantaneous, or single-epoch, high-precision GNSS is resistant to satellite signal interruptions which take place frequently in urban and other GNSS-difficult areas and thus is valued in time- and safety-critical applications. Single-epoch decimeter-level or better positioning is premised on ambiguity-fixed carrier-phase data and is thus mostly promised for ultra-short-baseline solutions (e.g., preferably < 10 km) (e.g., Odolinski et al. 2015; Prochniewicz et al. 2016; Teunissen et al. 2014). This is because precise enough ambiguity estimates for both successful integer-cycle resolution and high-precision positioning are hardly achievable in case of single epochs of data. The exception is that, in case of ultra-short baselines, various predominant spatially correlated GNSS errors (e.g., orbit anomalies, atmosphere refractions, etc.) cancel nearly completely, thus minimizing their contamination on ambiguity estimates. The major drawback of short-baseline solutions is that a very dense network of reference stations has to be pre-established, which is costly and unrealistic in remote areas. Precise point positioning (PPP), in contrast, is able to provide subdecimeter- to centimeter-level positions of global coverage without any nearby reference network (Zumberge et al. 1997). However, it is well known that a long initialization time of up to tens of minutes is required before high-precision positions can be achieved, rendering PPP almost useless in time-critical applications (e.g., Geng et al. 2010; Abd Rabbou and El-Rabbany 2016).

The turning point to enabling wide-area single-epoch high-precision positioning is the advent of multi-frequency GNSS signals. For example, Feng and Li (2010) formulated a strategy where two wide-lane combination GNSS observables, whose ambiguities could be resolved near instantaneously, were used to mitigate double-difference ionosphere delays. Single-epoch decimeter-level relative positioning was then implemented through a third ambiguity-fixed wide-lane observable. Tests through simulated triple-frequency GPS data showed that on average about 30 cm positioning accuracy for the horizontal components and 100 cm for the vertical could be attained epoch by epoch. Later, He et al. (2016) used real triple-frequency BeiDou data on medium baselines (e.g., 50–100 km) to realize the idea of Feng and Li (2010), but did not parameterize atmosphere delays in wide-lane positioning with the assumption that they were minimal overall. A success rate of over 98% was achieved for wide-lane ambiguity resolution using a single epoch of BeiDou data; an instantaneous positioning accuracy of better than 20 cm in the horizontal directions and better than 60 cm in the vertical was reached over a 24-h data span. However, if slant ionosphere delays were estimated in addition to positions and ambiguities, Li et al. (2017) showed that the single-epoch position estimates from medium BeiDou baselines could depart from the truth on average by about 50 cm in the horizontal components and 100 cm in the vertical.

In case of PPP, analogously, Geng and Bock (2013) used simulated triple-frequency GPS data to form an ionosphere-free ambiguity-fixed wide-lane observable of decimeter-level noise, through the aid of an extra-wide-lane observable. This strategy resembles that by Feng and Li (2010) in nature, but is formulated using undifferenced observables. The resulting near instantaneous positions reached an accuracy of a few decimeters (i.e., 20–60 cm) for all three components. Gu et al. (2015), alternatively, commenced from raw triple-frequency BeiDou observables, but later still mapped raw ambiguities into two wide-lane counterparts with the goal of speeding up narrow-lane ambiguity resolution. Due to the poor BeiDou satellite geometry, neither wide-lane ambiguity resolution could be accomplished within a few epochs. Rather, both required tens to hundreds of seconds of data.

In this study, we first integrate GPS, BeiDou, Galileo and Quazi-Zenith Satellite System (QZSS) triple-frequency data to enhance satellite geometry and further tightly couple them to achieve instantaneous decimeter-level positioning on a global scale, especially for the horizontal components. Since the multi-frequency satellite constellations of GPS, Galileo and QZSS are incomplete, a tight coupling by sharing a common reference satellite among all GNSS will improve the availability of resolvable ambiguities and also high-precision positions (e.g., Geng and Shi 2017; Geng et al. 2018; Odijk et al. 2017a). This paper is outlined as follows. Section 2 details the methods we developed to realize tightly coupled multi-GNSS instantaneous decimeter-level PPP. Section 3 exhibits the data and processing strategies. Results on ambiguity resolution achievement and single-epoch positioning performance at static stations and on a mobile vehicle are presented in Sect. 4, which will be followed by a discussion in Sect. 5 about high-dimensional ambiguity resolution. Conclusions and outlook are drawn in Sect. 6.

2 Methods

The undifferenced triple-frequency GNSS observation equations between station \(i\) and satellite \(k\) can be written as

$$\begin{aligned} \left\{ \begin{array}{l} \begin{aligned} P_{i,1}^{k}&{}=\rho _i^k+\gamma _i^k+d_{i,1}^{\mathrm {s}}-d_1^k\\ P_{i,2}^{k}&{}=\rho _i^k+g_{\mathrm {s},2}^2\gamma _i^k+d_{i,2}^{\mathrm {s}}-d_2^k\\ P_{i,3}^{k}&{}=\rho _i^k+g_{\mathrm {s},3}^2\gamma _i^k+d_{i,3}^{\mathrm {s}}-d_3^k \end{aligned} \end{array}\right. \end{aligned}$$
(1)

which is for pseudorange, and

$$\begin{aligned} \left\{ \begin{array}{l} \begin{aligned} L_{i,1}^{k}&{}=\rho _i^k-\gamma _i^k+\lambda _{\mathrm {s},1}N_{i,1}^k+b_{i,1}^{\mathrm {s}}-b_1^k\\ L_{i,2}^{k}&{}=\rho _i^k-g_{\mathrm {s},2}^2\gamma _i^k+\lambda _{\mathrm {s},2}N_{i,2}^k+b_{i,2}^{\mathrm {s}}-b_2^k\\ L_{i,3}^{k}&{}=\rho _i^k-g_{\mathrm {s},3}^2\gamma _i^k+\lambda _{\mathrm {s},3}N_{i,3}^k+b_{i,3}^{\mathrm {s}}-b_3^k \end{aligned} \end{array}\right. \end{aligned}$$
(2)

which is for carrier phase in the unit of length where “\(\mathrm {s}\)” represents “G” for GPS, “C” for BeiDou, “E” for Galileo or “J” for QZSS; \(\rho _i^k\) denotes non-dispersive delay between station i and satellite k including their geometric distance, the clock errors and the troposphere delay; \(\gamma _i^k\) is the first-order slant ionosphere delay on L1; \(g_{\mathrm {s},2}=\dfrac{f_{\mathrm {s},1}}{f_{\mathrm {s},2}}\) and \(g_{\mathrm {s},3}=\dfrac{f_{\mathrm {s},1}}{f_{\mathrm {s},3}}\) where \(f_{\mathrm {s},1}\), \(f_{\mathrm {s},2}\) and \(f_{\mathrm {s},3}\) are the frequencies of L1, L2 and L3 signals from GNSS “s”, respectively; \(N_{i,1}^k\), \(N_{i,2}^k\) and \(N_{i,3}^k\) denote the integer ambiguities; \(\lambda _{\mathrm {s},1}=\dfrac{c}{f_{\mathrm {s},1}}\), \(\lambda _{\mathrm {s},2}=\dfrac{c}{f_{\mathrm {s},2}}\) and \(\lambda _{\mathrm {s},3}=\dfrac{c}{f_{\mathrm {s},3}}\) where c is the speed of light in vacuum; \(d_{i,1}^{\mathrm {s}}\), \(d_{i,2}^{\mathrm {s}}\) and \(d_{i,3}^{\mathrm {s}}\) are GNSS-specific station hardware biases on pseudorange, while \(b_{i,1}^{\mathrm {s}}\), \(b_{i,2}^{\mathrm {s}}\) and \(b_{i,3}^{\mathrm {s}}\) are those on carrier phase; \(d_1^k\), \(d_2^k\) and \(d_3^k\) are satellite hardware biases on pseudorange, while \(b_1^k\), \(b_2^k\) and \(b_3^k\) are those on carrier phase; remaining error terms such as multi-path and higher-order ionosphere delays are ignored for brevity. Throughout this study, we use “L1”, “L2” and “L3” to generally represent L1, L2 and L5 signals from GPS and QZSS, B1, B2 and B3 from BeiDou, or E1, E5a and E5b from Galileo, respectively.

Equations 1 and 2 are the raw observation equations we directly employ in the Kalman filter of PPP, where, however, no station or satellite hardware biases (\(d_{i,1}^{\mathrm {s}}\), \(d_1^k\), \(b_{i,1}^{\mathrm {s}}\), \(b_1^k\), etc.) are parameterized due to their linear dependency on the clock and ambiguity parameters. As a result, they have to be combined with other parameters to be estimated (Odijk et al. 2017b; Zhang et al. 2012). Geng and Bock (2016) exemplified that these hardware biases, if time-invariable, could be assimilated entirely, without any residual fractions, into clocks, ionosphere delays and ambiguities in case of dual-frequency CDMA (code-division multiple access) signals. However, this situation deteriorates on the occasion of involving a third frequency signal. Montenbruck et al. (2011) reported that there existed time-varying inter-frequency clock biases (IFCBs) of up to 40 cm between the L1/L2 and L1/L5 GPS clocks, which was also observed for BeiDou, though much smaller (4 cm only) (e.g., Montenbruck et al. 2013). Guo and Geng (2018) later demonstrated in both theory and practice the connections between the satellite hardware biases and the IFCBs. Due largely to these IFCBs, station and satellite hardware biases cannot be absorbed perfectly into other parameters anymore if we insist on common clocks among the three frequencies in undifferenced data processing. Guo and Geng (2018) therefore proposed to estimate a second satellite clock parameter and a constant receiver clock bias for the third frequency signals. Specifically, the legacy L1/L2 carrier phases from a particular satellite share one satellite clock parameter, while the L3 carrier phase monopolizes the second which is intended to absorb the time-varying IFCBs; meanwhile, a station-specific constant unknown is estimated using the L3 pseudorange to address its differing code bias from those within L1/L2 pseudorange. In this case, we can reconcile all hardware biases when assimilating them into the other parameters to be estimated for the three frequencies. In this paper, however, we do not expand Eqs. 1 or 2 to illustrate how the second satellite clock is parameterized, and interested readers can refer to Guo and Geng (2018) for more mathematics.

2.1 Inter-system phase bias (ISPB) estimation

ISPBs can be taken as the station-specific biases that prevent the formation of resolvable inter-GNSS ambiguities (Odijk and Teunissen 2013). They will be quite useful when there are few satellites available within each GNSS, since inter-GNSS ambiguities can be composed in addition to the few intra-GNSS counterparts. This means that the number of resolvable ambiguities is increased, and the availability of ambiguity-fixed solutions is improved consequently (Odijk et al. 2017a). We can hence exploit all carrier-phase data for the highest efficiency of ambiguity resolution. This scenario is especially true regarding the minority of triple-frequency GNSS satellites at the moment. Therefore, for this study, we apply the method developed by Geng et al. (2018) to calculate ISPBs across GNSS.

From the PPP processing based on Eqs. 1 and 2, we can obtain undifferenced ambiguity estimates on all three frequencies (i.e., \(\hat{N}_{i,1}^k\), \(\hat{N}_{i,2}^k\) and \(\hat{N}_{i,3}^k\)) and then derive

$$\begin{aligned} \left\{ \begin{array}{l} \hat{N}_{i,\mathrm {ew}}^k=\hat{N}_{i,2}^k-\hat{N}_{i,3}^k=\breve{N}_{i,\mathrm {ew}}^k+{\bar{\beta }}_{i,\mathrm {ew}}^{\mathrm {s}}-{\bar{\beta }}_\mathrm {ew}^k\\ \hat{N}_{i,\mathrm {w}}^k=\hat{N}_{i,1}^k-\hat{N}_{i,2}^k=\breve{N}_{i,\mathrm {w}}^k+{\bar{\beta }}_{i,\mathrm {w}}^{\mathrm {s}}-{\bar{\beta }}_\mathrm {w}^k \end{array}\right. \end{aligned}$$
(3)

where \(\hat{N}_{i,\mathrm {ew}}^k\) and \(\hat{N}_{i,\mathrm {w}}^k\) are the extra-wide-lane and wide-lane ambiguity estimates (or often abbreviated as “the two wide-lane” hereafter for brevity), which are not integers because of the contamination of hardware biases (or uncalibrated phase delay, UPD, by Ge et al. 2008); \(\breve{N}_{i,\mathrm {ew}}^k\) and \(\breve{N}_{i,\mathrm {w}}^k\) are nominal integer ambiguities since they absorb the integer parts of hardware biases; \({\bar{\beta }}_{i,\mathrm {ew}}^{\mathrm {s}}\) and \({\bar{\beta }}_{i,\mathrm {w}}^{\mathrm {s}}\) denote the fractional parts of station hardware biases, whereas \({\bar{\beta }}_\mathrm {ew}^k\) and \({\bar{\beta }}_\mathrm {w}^k\) are the fractional parts of satellite hardware biases. We hereafter define these “\({\bar{\beta }}\)” quantities as fractional-cycle biases (FCBs).

We then form double-difference ambiguities between stations i and j and satellites k and q using the estimates in Eq. 3 to eliminate satellite FCBs, that is

$$\begin{aligned} \left\{ \begin{array}{l} \hat{N}_{ij,\mathrm {ew}}^{kq}=\breve{N}_{ij,\mathrm {ew}}^{kq}+{\bar{\beta }}_{i,\mathrm {ew}}^{\mathrm {s_1s_2}}-{\bar{\beta }}_{j,\mathrm {ew}}^{\mathrm {s_1s_2}}\\ \hat{N}_{ij,\mathrm {w}}^{kq}=\breve{N}_{ij,\mathrm {w}}^{kq}+{\bar{\beta }}_{i,\mathrm {w}}^{\mathrm {s_1s_2}}-{\bar{\beta }}_{j,\mathrm {w}}^{\mathrm {s_1s_2}} \end{array}\right. \end{aligned}$$
(4)

where

$$\begin{aligned} \left\{ \begin{array}{l} \hat{N}_{ij,*}^{kq}=\hat{N}_{i,*}^k-\hat{N}_{i,*}^q-\hat{N}_{j,*}^k+\hat{N}_{j,*}^q\\ \breve{N}_{ij,*}^{kq}=\breve{N}_{i,*}^k-\breve{N}_{i,*}^q-\breve{N}_{j,*}^k+\hat{N}_{j,*}^q\\ {\bar{\beta }}_{i,*}^{\mathrm {s_1s_2}}={\bar{\beta }}_{i,*}^{\mathrm {s_1}}-{\bar{\beta }}_{i,*}^{\mathrm {s_2}}\\ {\bar{\beta }}_{j,*}^{\mathrm {s_1s_2}}={\bar{\beta }}_{j,*}^{\mathrm {s_1}}-{\bar{\beta }}_{j,*}^{\mathrm {s_2}} \end{array}\right. \end{aligned}$$

and “\(*\)” is a wildcard representing “ew” or “w”; satellite k belongs to GNSS “\(\mathrm {s_1}\),” while satellite q to “\(\mathrm {s_2}\)”; \({\bar{\beta }}_{i,\mathrm {ew}}^{\mathrm {s_1s_2}}\) and \({\bar{\beta }}_{j,\mathrm {ew}}^{\mathrm {s_1s_2}}\) are the extra-wide-lane ISPBs at stations i and j, respectively, whereas \({\bar{\beta }}_{i,\mathrm {w}}^{\mathrm {s_1s_2}}\) and \({\bar{\beta }}_{j,\mathrm {w}}^{\mathrm {s_1s_2}}\) are the wide-lane ISPBs. Note that these ISPBs will equate zero if “\(\mathrm {s_1}\)” is the same as “\(\mathrm {s_2}\)”, or in other words satellites k and q come from the same GNSS.

For simplicity, we presume that the differential ISPBs \(\left( {\bar{\beta }}_{i,\mathrm {ew}}^{\mathrm {s_1s_2}}-{\bar{\beta }}_{j,\mathrm {ew}}^{\mathrm {s_1s_2}}\right) \) and \(\left( {\bar{\beta }}_{i,\mathrm {w}}^{\mathrm {s_1s_2}}-{\bar{\beta }}_{j,\mathrm {w}}^{\mathrm {s_1s_2}}\right) \) between stations i and j are still fractional. Then we can apply integer rounding to Eq. 4 to separate differential ISPBs from the nominal integer ambiguities (Geng et al. 2018), that is

$$\begin{aligned} \left\{ \begin{array}{l} {\hat{\beta }}_{i,\mathrm {ew}}^{\mathrm {s_1s_2}}-{\hat{\beta }}_{j,\mathrm {ew}}^{\mathrm {s_1s_2}}=\hat{N}_{ij,\mathrm {ew}}^{kq}-\left[ \hat{N}_{ij,\mathrm {ew}}^{kq}\right] \\ {\hat{\beta }}_{i,\mathrm {w}}^{\mathrm {s_1s_2}}-{\hat{\beta }}_{j,\mathrm {w}}^{\mathrm {s_1s_2}}=\hat{N}_{ij,\mathrm {w}}^{kq}-\left[ \hat{N}_{ij,\mathrm {w}}^{kq}\right] \end{array}\right. \end{aligned}$$
(5)

where \(\left[ \cdot \right] \) denotes an integer rounding operation. Differential ISPB estimates can then to converted into undifferenced (pseudo-absolute) values by assigning a reference ISPB. The ISPB computation process is illustrated in Fig. 1.

2.2 Inter-system fractional-cycle bias (FCB) estimation

FCBs are crucial to the recovery of the integer properties of PPP ambiguities (Ge et al. 2008). The satellite FCB estimation is straightforward for intra-system ambiguities (Geng and Bock 2013). However, inter-system satellite FCB estimation requires a pre-calibration of station ISPBs. From Eq. 3, we can form single-difference (extra-)wide-lane ambiguities at station i between a pair of satellites (k and q) belonging to different GNSS, that is

$$\begin{aligned} \left\{ \begin{array}{l} \hat{N}_{i,\mathrm {ew}}^{kq}=\breve{N}_{i,\mathrm {ew}}^{kq}+{\bar{\beta }}_{i,\mathrm {ew}}^{\mathrm {s_1s_2}}-{\bar{\beta }}_\mathrm {ew}^{kq}\\ \hat{N}_{i,\mathrm {w}}^{kq}=\breve{N}_{i,\mathrm {w}}^{kq}+{\bar{\beta }}_{i,\mathrm {w}}^{\mathrm {s_1s_2}}-{\bar{\beta }}_\mathrm {w}^{kq} \end{array}\right. \end{aligned}$$
(6)

where

$$\begin{aligned} \left\{ \begin{array}{l} \hat{N}_{i,*}^{kq}=\hat{N}_{i,*}^k-\hat{N}_{i,*}^q\\ \breve{N}_{i,*}^{kq}=\breve{N}_{i,*}^k-\breve{N}_{i,*}^q \end{array}\right. \end{aligned}$$

and \({\bar{\beta }}_*^{kq}={\bar{\beta }}_*^k-{\bar{\beta }}_*^q\) which is the inter-system (between GNSS “\(\mathrm {s_1}\)” and “\(\mathrm {s_2}\)”) satellite FCBs. We can subsequently correct for ISPBs derived from Eq. 5 and obtain

$$\begin{aligned} \left\{ \begin{array}{l} \hat{N}_{i,\mathrm {ew}}^{kq}-{\hat{\beta }}_{i,\mathrm {ew}}^{\mathrm {s_1s_2}}=\breve{N}_{i,\mathrm {ew}}^{kq}-{\bar{\beta }}_\mathrm {ew}^{kq}\\ \hat{N}_{i,\mathrm {w}}^{kq}-{\hat{\beta }}_{i,\mathrm {w}}^{\mathrm {s_1s_2}}=\breve{N}_{i,\mathrm {w}}^{kq}-{\bar{\beta }}_\mathrm {w}^{kq} \end{array}\right. \end{aligned}$$
(7)

Similar to Eq. 5, we can further compute satellite pair FCBs

$$\begin{aligned} \left\{ \begin{array}{l} {\hat{\beta }}_\mathrm {ew}^{kq}=\left[ \hat{N}_{i,\mathrm {ew}}^{kq}-{\hat{\beta }}_{i,\mathrm {ew}}^{\mathrm {s_1s_2}}\right] -\left( \hat{N}_{i,\mathrm {ew}}^{kq}-{\hat{\beta }}_{i,\mathrm {ew}}^{\mathrm {s_1s_2}}\right) \\ {\hat{\beta }}_\mathrm {w}^{kq}=\left[ \hat{N}_{i,\mathrm {w}}^{kq}-{\hat{\beta }}_{i,\mathrm {w}}^{\mathrm {s_1s_2}}\right] -\left( \hat{N}_{i,\mathrm {w}}^{kq}-{\hat{\beta }}_{i,\mathrm {w}}^{\mathrm {s_1s_2}}\right) \end{array}\right. \end{aligned}$$
(8)

which can also be converted into undifferenced values given a zero reference satellite FCB. Similarly, the FCB computation is described in Fig. 1.

Fig. 1
figure 1

Flowchart of inter-system ISPB and FCB computations. “DD” and “SD” denote double- and single-difference, respectively. “Rounding” indicates separating fractional parts of those DD and SD ambiguities. Note that inter-system SD ambiguities can only be formed after ISPBs are corrected. “Averaging” indicates calculating the mean of those fractional parts; for ISPBs, this averaging is carried out over all inter-system satellite pairs at a station; for FCBs, this averaging is performed over all stations observing an inter-system satellite pair. Equation labels from Sects. 2.1 and 2.2 are also plotted inside the panels

Full size image

2.3 Instantaneous PPP wide-lane ambiguity resolution (PPP-WAR)

ISPBs and FCBs are computed at the server end. At the user end for inter-system PPP-WAR, station ISPBs and satellite FCBs have to be calibrated in order to retrieve resolvable ambiguities that have integer nature. Here we commence from Eqs. 1 and 2 again. For any epoch of data at a particular station, we need to choose a reference GPS satellite to form single-difference ambiguities with respect to the remaining satellites to remove station-specific FCBs. We can afterward map the single-difference ambiguities and their variance–covariance matrix into (extra-)wide-lane counterparts (Dong and Bock 1989). The mapping matrix takes the form of

$$\begin{aligned} \left( \begin{array}{c} \hat{N}_{i,\mathrm {ew}}^{kq} \\ \hat{N}_{i,\mathrm {w}}^{kq} \\ \hat{N}_{i,1}^{kq} \end{array}\right) =\left( \begin{array}{rrr} 0 &{}\quad 1 &{}\quad -\,1 \\ 1 &{}\quad -\,1 &{}\quad 0 \\ 1 &{}\quad 0 &{}\quad 0 \end{array}\right) \left( \begin{array}{c} \hat{N}_{i,1}^{kq} \\ \hat{N}_{i,2}^{kq} \\ \hat{N}_{i,3}^{kq} \end{array}\right) \end{aligned}$$
(9)

where satellite k belongs to GPS and satellite q to GPS, BeiDou, Galileo or QZSS. We then obtain the (extra-)wide-lane ambiguity estimates again (Eq. 6) and they need to be corrected for ISPBs and FCBs, that is

$$\begin{aligned} \left\{ \begin{array}{l} \breve{N}_{i,\mathrm {ew}}^{kq}=\hat{N}_{i,\mathrm {ew}}^{kq}-{\hat{\beta }}_{i,\mathrm {ew}}^\mathrm {Gs_2}+{\hat{\beta }}_\mathrm {ew}^{kq}\\ \breve{N}_{i,\mathrm {w}}^{kq}=\hat{N}_{i,\mathrm {w}}^{kq}-{\hat{\beta }}_{i,\mathrm {w}}^\mathrm {Gs_2}+{\hat{\beta }}_\mathrm {w}^{kq} \end{array}\right. \end{aligned}$$
(10)

where “\(\mathrm {s_2}\)” can be GPS, BeiDou, Galileo or QZSS. We note that \(\breve{N}_{i,\mathrm {ew}}^{kq}\) and \(\breve{N}_{i,\mathrm {w}}^{kq}\) are now resolvable (extra-)wide-lane ambiguities in PPP. To explain more clearly, we obtained \(\breve{N}_{i,\mathrm {ew}}^{kq}\) and \(\breve{N}_{i,\mathrm {w}}^{kq}\) by simply deducting ISPBs \({\hat{\beta }}_{i,\mathrm {ew}}^\mathrm {Gs_2}\) and \({\hat{\beta }}_{i,\mathrm {w}}^\mathrm {Gs_2}\), and FCBs \({\hat{\beta }}_\mathrm {ew}^{kq}\) and \({\hat{\beta }}_\mathrm {w}^{kq}\) from the PPP ambiguity estimates \(\hat{N}_{i,\mathrm {ew}}^{kq}\) and \(\hat{N}_{i,\mathrm {w}}^{kq}\); of particular note, \(\breve{N}_{i,\mathrm {ew}}^{kq}\) and \(\breve{N}_{i,\mathrm {w}}^{kq}\) still share the variance–covariance matrix of \(\hat{N}_{i,\mathrm {ew}}^{kq}\) and \(\hat{N}_{i,\mathrm {w}}^{kq}\); it is then this variance–covariance matrix and \(\breve{N}_{i,\mathrm {ew}}^{kq}\) and \(\breve{N}_{i,\mathrm {w}}^{kq}\) that are injected into the least-squares ambiguity decorrelation adjustment (LAMBDA) engine to search for their integer candidates (Teunissen 1995).

One important point worthy of attention is that we should leverage the easily resolved extra-wide-lane ambiguities to improve the resolvability of their wide-lane counterparts. To be specific, after fixing extra-wide-lane ambiguities to integers, we should apply these integers as hard constraints to the normal matrix and hence update the wide-lane ambiguity estimates and their variance–covariance matrix (refer to Dong and Bock 1989). The resulting wide-lane ambiguities are then corrected for wide-lane ISPBs and FCBs preceding their integer-cycle resolution. A successful wide-lane ambiguity resolution afterward using a single epoch of data completes PPP-WAR for instantaneous decimeter-level positioning. We note that here extra-wide-lane and wide-lane ambiguity resolution can also be accomplished in one LAMBDA search where the former has to be resolved first in the bootstrapping.

3 Data processing

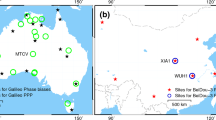
We collected 30-s triple-frequency multi-GNSS data spanning days 335–365 in 2017 at 107 stations from International GNSS Service—Multi-GNSS Experiment (IGS-MGEX) and Australian Regional GNSS Network (ARGN) (Fig. 2). These stations consisted of 49 Trimble, 14 Leica, 8 Javad and 36 Septentrio receivers. We employed the predicted orbits and Earth rotation parameters (ERPs) updated every 3 h by GFZ (German Research Centre for Geosciences). Pseudorange and carrier-phase data on GPS/QZSS L1/L2/L5, BeiDou Inclined Geosynchronous Orbiter/Medium Earth orbiter (IGSO/MEO) B1/B2/B3 and Galileo E1/E5a/E5b were processed in undifferenced mode and weighted according to elevation-scaled a priori precisions of 0.2 m and 2 mm, respectively. A cutoff angle of 10\(^\circ \) was used to rule out low-elevation observations. We applied the Differential Code Bias (DCB) corrections provided by Center for Orbit Determination in Europe (CODE) and the elevation-dependent bias corrections for BeiDou IGSO/MEO (Wanninger and Beer 2015). Residual zenith troposphere delays (ZTDs) after the a priori Saastamoinen modeling were computed every 1 h as random-walk parameters with a process noise of 2 cm/\(\sqrt{\mathrm {hour}}\), and projected onto slant directions using the global mapping functions (Boehm et al. 2006; Saastamoinen 1973). Likewise, slant ionosphere delays were modeled as random-walk parameters with a loose constraint of 25 m/\(\sqrt{\mathrm {epoch}}\). IGS absolute antenna phase center offsets and variations (PCO/PCV) were applied (igs14_1986.atx). We presumed that GPS L5 signals shared the PCO/PCV of L2 at the satellite end, while at the station end all BeiDou, Galileo and QZSS signals shared the PCO/PCV of GPS and the third frequency signals had the same corrections as those for L2. Based on these settings, satellite clocks were estimated in a simulated real-time mode using the 70 globally distributed stations denoted as open circles in Fig. 2. Subsequently, by fixing satellite orbits, clocks and ERPs, we computed daily differential (extra-)wide-lane ISPBs for BeiDou, Galileo and QZSS with respect to GPS between all pairs of stations distanced by less than 4000 km. After corrections for ISPBs at the 70 reference stations, daily differential FCBs were estimated between a GPS satellite and all other remaining satellites. In addition, we have to acknowledge that, in this study for proof of concept, we did not consider all possible latencies of the clock, ISPB or FCB products before enabling a true real-time PPP-WAR. However, we believe that such latency problems can be resolved at a high confidence level, if we know well the temporal properties of those products (see Sects. 4.1, 4.2) and have an appropriate functional and stochastic model to predict them over time, as prominently demonstrated by Wang et al. (2017).

Fig. 2
figure 2

Distribution of International GNSS Service (IGS) and Australian Regional GNSS Network (ARGN) stations recording multi-constellation and multi-frequency GNSS data. Seventy stations denoted as open circles are used to estimate satellite clock and FCB (fractional-cycle bias) products, while the other 37 as crosses to test PPP. “G”, “C”, “E” and “J” represent GPS, BeiDou, Galileo and QZSS, respectively

Full size image

In Fig. 2, we chose 37 globally distributed stations denoted as crosses to test PPP-WAR. Owing to the sparsity of triple-frequency GNSS stations in America, Africa and Asia, most PPP stations were located in Europe and Australia. Most data processing settings at these PPP stations were the same as those at the 70 reference stations. However, we did not estimate residual ZTDs in instantaneous positioning; ionosphere delays were estimated as white noise parameters. Here we should reiterate that only a single epoch of data was used to compute positions in our “instantaneous” PPP-WAR, suggesting that neither atmosphere nor ambiguity parameters were smoothed over multiple epochs. Furthermore, only ambiguities corresponding to elevations of larger than 10\(^\circ \) were allowed to enter the process of integer-cycle resolution; we searched for their integer candidates using the LAMBDA method; the resulting integer (extra-)wide-lane candidates were then validated using the ratio test with a threshold of 2.0 (Euler and Schaffrin 1990). We also enabled partial ambiguity resolution to exclude possibly biased ambiguities. It was mandated that at most four ambiguities could be precluded, while at least five must be reserved for a LAMBDA search. Of particular note, if partial ambiguity resolution still failed ultimately, we chose to fix the ambiguities to the candidate integers corresponding to the largest ratio value we had found, rather than keep a float epoch. In this case, we could always achieve an ambiguity-fixed solution at each epoch, albeit risking identifying incorrect integers.

More interestingly, we also carried out a PPP-WAR test on a vehicle on April 17, 2018, in Wuhan city (near station JFNG in Fig. 2). We drove the vehicle along a quasi-square route escorted by a number of structures and trees, one tunnel and two crossovers (Fig. 3). The length of the route totaled about 6 km which took about 12 min of driving; we drove four laps from about 9:00 until 10:00 UTC (Coordinated Universal Time). We had one Trimble NetR9 receiver at the reference station placed at the northeastern corner with an open sky view, while another fixed on top of the vehicle collecting GPS/BeiDou/Galileo/QZSS triple-frequency observations at a 10 Hz sampling rate. Both receivers were connected with Zephyr Geodetic 2 antennas. We first calculated the precise position of the reference station relative to IGS station JFNG located about 4.6 km away (Fig. 2). The benchmark positions of the vehicle trajectory were afterward computed with respect to this reference station. The fixing rate of double-difference ambiguities was over 99%, suggesting a high-quality truth benchmark. Moreover, for the PPP-WAR solution of the vehicle trajectory, we used the same reference network shown in Fig. 2 to estimate the station ISPB, satellite clock and FCB products. The vehicle-borne GNSS data were processed according to the same strategy as that for the static stations in Fig. 2.

Fig. 3
figure 3

Vehicle trajectory denoted as yellow lines. The length of the quasi-square route totals about 6 km, and the vehicle drove four laps clockwise. The green solid circle at the top right corner denotes the position of the reference station. Three red solid bars along the route represent one tunnel and two crossovers. The inset shows the number of satellites and the position dilution of precision (PDOP) values during the kinematic experiment. This map is thankfully from Google Earth

Full size image

4 Results

4.1 Inter-system phase biases (ISPBs)

Station-specific ISPBs are the key to tightly coupling multi-GNSS carrier-phase data. Collecting the (extra-)wide-lane ambiguity estimates from all 107 stations in Fig. 2, we formed double-difference ambiguities between GPS and non-GPS satellites for all eligible station pairs on each day. Their fractional parts were then separated from all these double-difference ambiguities and afterward averaged for each day with respect to each station pair to estimate differential ISPBs between GPS and BeiDou, GPS and Galileo, and GPS and QZSS. Here we can sense that ISPB uncertainties are subject to the agreement among all involved fractional parts of double-difference ambiguities. In fact, more than 98% of such extra-wide-lane and over 83% of wide-lane fractional parts agreed well within ± 0.15 cycles on average over all stations. The mean RMS of all extra-wide-lane and wide-lane fractional parts after removal of ISPBs was around 0.04 cycles and 0.11 cycles, respectively. These statistics demonstrate that extra-wide-lane ISPBs have been quite precisely determined, while wide-lane ISPBs may have been less but still satisfactory to ensure highly efficient ambiguity resolution.

Moreover, as stressed in Sect. 3, in case of real-time scenarios, we are especially concerned about the temporal stability of ISPBs. In the top panels of Fig. 4, we show a typical ISPB time series for baseline MEDO–KARR over the 31 days. At a first glance, the extra-wide-lane ISPBs are indeed nonzero and differ among GNSS pairs, but are quite stable over time with negligible variations of less than 0.05 cycles most of the time. In contrast, the wide-lane ISPBs can behave less steadily and sometimes reveal sudden jumps, such as those for GPS–BeiDou in the top-left panel. This observation echoes that presented by Geng et al. (2018) where the irregular subdaily signatures of ISPBs degrade their temporal stability. Furthermore, the bottom three panels of Fig. 4 illustrate the distribution of ISPB variations for GPS–BeiDou, GPS–Galileo and GPS–QZSS. As expected, the extra-wide-lane ISPB variation from day to day is minimal where over 90% are smaller than 0.05 cycles. This favorable performance can be ascribed to the super long wavelength of extra-wide-lane observables (several meters), greatly overshadowing the contaminating hardware biases. However, this statistics drops considerably to 70% or even lower in case of wide-lane ISPBs, confirming the observation of more pronounced wide-lane ISPB fluctuations within the top three panels. The GPS–BeiDou wide-lane ISPBs appear to perform worse than the GPS–Galileo and GPS–QZSS counterparts in terms of temporal stability. However, this inferiority goes almost unnoticed in case of the variation threshold of 0.1 cycles where all percentages concerning the day-to-day wide-lane ISPB changes rise to around 85%. We therefore demonstrate that both extra-wide-lane and wide-lane ISPBs are fairly stable over time, which will in general facilitate their precise predictions for real-time PPP-WAR. To be specific, we can predict ISPBs precisely for the next few days using their estimates on preceding days to enable real-time applications; higher-precision predictions can be achieved if the prediction interval is shortened to hours or even minutes (e.g., Geng et al. 2011).

Fig. 4
figure 4

Daily ISPBs (cycle) from days 335 to 365 and the distribution of their variations across neighboring days. The top three panels exemplify the differential daily (extra-)wide-lane ISPBs for BeiDou, Galileo and QZSS with respect to GPS at station pair MEDO–KARR (see Fig. 2). Correspondingly, the bottom panels show the distribution of (extra-)wide-lane ISPB variations from day to day over all station pairs. Percentages for the ISPB variations falling in ± 0.05 and ± 0.1 cycles are plotted at the top of each bottom panel

Full size image

4.2 Inter-system fractional-cycle biases (FCBs)

Once ISPBs are computed, we can estimate inter-system FCBs specific to inter-GNSS satellite pairs. In this study, we first corrected for ISPBs at the 70 reference stations in Fig. 2, from which we further formed single-difference (extra-)wide-lane ambiguity estimates between GPS and non-GPS satellites. The fractional parts of these single-difference ambiguities were identified afterward for each satellite pair and then averaged over all involved stations to compute inter-system satellite FCBs. We achieved that on average over 99% of all fractional parts specific to a given satellite pair agreed quite well to ± 0.15 cycles, and the mean RMS of these fractional parts after removal of FCBs was less than 0.05 cycles. Therefore, it is demonstrated that the inter-system FCB products have been precisely estimated in this study.

Similarly, we further investigated the temporal behavior of inter-system (extra-)wide-lane satellite FCBs. Figure 5 shows the distribution of FCB variations across neighboring days. Regarding the inter-system FCBs only, the extra-wide-lane FCBs have much better temporal stabilities than the wide-lane FCBs. Moreover, inter-GPS/Galileo wide-lane FCBs, notably, have the highest temporal stability compared to the inter-GPS/BeiDou and inter-GPS/QZSS counterparts, agreeing with the statistics on the wide-lane ISPB stabilities reported in Fig. 4. However, such highest stability (85% within ± 0.05 cycles) is still easily dwarfed by that (99.1% within ± 0.05 cycles) of intra-GPS wide-lane FCBs presented in the top-left panel of Fig. 5. We postulate that the ISPB corrections derived in Sect. 4.1 may compromise the temporal stability of inter-system wide-lane FCBs. A confirmatory re-computation proves expectedly that the intra-BeiDou, intra-Galileo and intra-QZSS wide-lane FCBs, which are unassociated with ISPBs, have over 82%, 93% and 91% day-to-day variations within ± 0.05 cycles, respectively, as opposed to about 54%, 85% and 76% for the inter-GPS/BeiDou, inter-GPS/Galileo and inter-GPS/QZSS counterparts. Therefore, we conclude that the instability of station ISPBs does affect adversely the temporal behaviors of inter-system satellite FCBs.

Table 1 Success rates of ambiguity-fixed epochs in cases of tightly and loosely coupled multi-GNSS instantaneous PPP-WAR at all 107 stations over the 31 days
Full size table
Fig. 5
figure 5

Distribution of extra-wide-lane (EWL) and wide-lane (WL) FCB variations (cycle) across neighboring days. We show four types of FCBs including intra-GPS, inter-GPS/BeiDou, inter-GPS/Galileo and inter-GPS/QZSS. Percentages for the day-to-day FCB variations falling in ± 0.05 and ± 0.1 cycles are presented at the top of each panel

Full size image

As in the case for ISPBs, FCBs have also to be predicted over time to enable a true real-time PPP-WAR. We have found that day-to-day FCB variations are as small as 0.1 cycles, and even smaller variations can be achieved between neighboring subdaily, instead of 24-h, FCB estimates, as reported by Geng and Bock (2016) and Gu et al. (2015). Therefore, in practice, both ISPB and FCB predictions should be made carefully by considering their temporal properties over various timescales before a pragmatic and reliable real-time PPP-WAR could be implemented.

4.3 Instantaneous PPP-WAR at static stations

Once obtaining the ISPB and FCB corrections, we used all 107 stations in Fig. 2 to test instantaneous PPP-WAR. For each station, we performed (extra-)wide-lane partial ambiguity resolution at every epoch independently. An attempt to resolve ambiguities at a particular epoch would be considered successful if these ambiguities were fixed to the same integers for the succeeding 20 epochs (i.e., 10 min). Table 1 shows the success rates of ambiguity-fixed epochs in cases of tightly and loosely coupled multi-GNSS instantaneous PPP-WAR. Loose coupling means that no ISPBs are introduced, and only intra-system ambiguities are formed for integer-cycle resolution. As expected, fixing extra-wide-lane ambiguities has the highest success rates which reach almost 100% by virtue of their super long wavelengths; this prominent performance is not subject to the satellite number or position dilution of precision (PDOP) values (Table 2). Partial ambiguity resolution contributes negligibly to this achievement since its resultant fixed epochs account for only 1–2% of all successfully fixed epochs. This implies that a full integer-cycle resolution is usually possible for extra-wide-lane ambiguities. However, this is not the case for wide-lane ambiguities. As illustrated by the quantities bracketed in the third column of Table 1, at up to 50% of fixed epochs, only a subset of wide-lane ambiguities are resolved. This implies that it is much more difficult to achieve wide-lane ambiguity resolution using a single epoch; overall, only about 70% of epochs achieve such instantaneity. This can be understood in terms of the much shorter wavelengths of wide-lane observables than those of their extra-wide-lane counterparts.

Fortunately, instantaneous wide-lane ambiguity resolution can be more efficiently attained if the resolved extra-wide-lane ambiguities are introduced to improve the wide-lane ambiguity estimates and their variance–covariance matrix (refer to Dong and Bock 1989). As exhibited in the last column of Table 1, about 90% of epochs have their wide-lane ambiguities fixed to correct integers. Table 2 further demonstrates that this percentage rises with the increasing satellite number and the decreasing PDOP values. Meanwhile, the contribution of partial ambiguity resolution to instantaneous wide-lane fixing declines considerably to 20–30%. In addition, tightly coupling multi-GNSS also improves the instantaneity of wide-lane ambiguity fixing, though slightly by rendering an extra 3–4% of epochs fixed instantly. Finally, we demonstrate that extra-wide-lane ambiguity resolution is highly efficient as single-epoch fixing is almost 100% achievable; instantaneous wide-lane ambiguity resolution, in contrast, can achieve a success rate of over 90% under the premise of fixed extra-wide-lane ambiguities; tightly coupled, in contrast to loosely coupled, multi-GNSS can further improve the instantaneity of PPP-WAR.

Table 2 Success rates of ambiguity-fixed epochs and instantaneous positioning errors (meter) for the east, north and up components with respect to the satellite number and PDOP values at the 107 stations in Fig. 2
Full size table
Fig. 6
figure 6

Position differences (meter) between instantaneous PPP-WAR solutions and daily position estimates for the east, north and up components at stations WILU and DLF1 on December 31 and 2, 2017, respectively (see Fig. 2 for the station locations). WILU collected triple-frequency observations from GPS, BeiDou, Galileo and QZSS, while DLF1 only from GPS and Galileo. “Single-epoch PPP” is also presented as a comparison to instantaneous PPP-WAR whose only difference is that the former does not resolve ambiguities. The RMS of their position differences from daily estimates is shown at the bottom of the top six panels. The dashed green horizontal lines within the top two rows of panels denote ± 0.3 m, while those in the third row of panels denote ± 0.5 m. The bottom two panels exhibit the number of visible satellites and the PDOP values at the two stations

Full size image

Correct ambiguity resolution normally improves positioning accuracy. Figure 6 shows the typical position differences of instantaneous PPP-WAR at two representative stations (WILU and DLF1 in Fig. 2) from their daily positions which are taken as truth benchmarks in this study. A “single-epoch PPP” solution is also shown as a comparison whose only difference from instantaneous PPP-WAR is that no ambiguities are resolved. “Instantaneous PPP-WAR” can also be alternatively taken as “WAR imposed on single-epoch PPP”. Station WILU is located in Australia capable of observing a good number of triple-frequency satellites from GPS, BeiDou, Galileo and QZSS, while DLF1 is in Europe where most observations are from GPS and Galileo only; as shown in the bottom panels, the satellites observed at WILU outnumber those at DLF1 almost twice. A larger number of satellites usually mean a smaller PDOP; the PDOP values for WILU remain below 2 for all 24 h while those for DLF1 frequently exceed 2. As a result, the horizontal RMS positioning errors of PPP-WAR at DLF1 almost double those at WILU, especially from 15:00 until 20:00 when the satellite number is around six only and the PDOP values go over 3. Overall, however, both stations achieve a great improvement in terms of positioning errors through instantaneous PPP-WAR, as opposed to single-epoch PPP. Specifically, the RMS positioning errors are reduced from 0.38, 0.39 and 0.89 m in case of single-epoch PPP to 0.14, 0.13 and 0.54 m in case of instantaneous PPP-WAR for the east, north and up component at station WILU, remarkably showing a 60% and 40% improvement for the horizontal and vertical components, respectively. About 90% of epochs have smaller than 0.3 m horizontal positioning errors after PPP-WAR, while only 34% in case of single-epoch PPP. With regard to DLF1, its RMS reductions due to PPP-WAR also, outstandingly, reach 40–50% for all three components. The position errors at over 64% of epochs stay below 0.3 m for the horizontal components. These facts convey that instantaneous PPP-WAR will achieve better positioning accuracy when more satellites contribute, but pronounced improvements can still be expected in case of incomplete GPS and Galileo triple-frequency constellations only.

Fig. 7
figure 7

Improvement of instantaneous positioning accuracy at each station shown in Fig. 2. The positioning accuracy is gauged in terms of RMS of the differences between epoch-wise and daily positions. We calculated the RMS improvement in the horizontal components by comparing the instantaneous PPP-WAR with the single-epoch PPP solutions. The station-specific color-coded RMS improvements are presented against the gray-coded satellite visibility on a global scale

Full size image

Other than only two stations inspected in Fig. 6, Table 2 shows the mean positioning errors of instantaneous PPP-WAR against the satellite number and PDOP values over all 107 stations. Outlier positions were identified if either horizontal component had an absolute error of over 3 m. In total, 0.47% of solutions are excluded for the statistics in Table 2. We can clearly see that when the satellite number rises from 6–8 to more than 15, the positioning errors of instantaneous PPP-WAR keep declining steadily from over 0.4 m to around 0.2 m in the horizontal and from about 1.2 to 0.6 m in the vertical components. The positioning errors of single-epoch PPP generally follow this tendency as well, but they fall relatively slowly against the satellite number. To be specific, when the satellite number exceeds 9, the RMS of single-epoch PPP stays around 0.5 m in the horizontal and 1.1 m in the vertical components. Similar tendency can also be noticed with respect to the PDOP values. Contrasting the RMS between instantaneous PPP-WAR and single-epoch PPP (i.e., instantaneous PPP without WAR), we can draw a conclusion that WAR plays a more and more important role in ameliorating instantaneous positioning accuracy, with respect to the increasing satellite number and the decreasing PDOP values.

To enhance the finding drawn from Table 2, Fig. 7 investigates how the reduction of RMS positioning errors owing to WAR imposed on single-epoch PPP relates to station locations. The mean RMS reductions in the horizontal components are computed for each station over the 31 days and then color-coded as shown within the filled circles of Fig. 7. Warmer colors denote greater RMS reductions. Meanwhile, the mean number of triple-frequency GNSS satellites that can be tracked at each corner of the globe is gray-coded where larger numbers correspond to darker gray. As expected, due to the concentration of BeiDou and QZSS satellites over Asia, 12–18 satellites can be observed in southeast Asia and Australia. As a result, it is this area that delivers the most significant RMS reductions contributed by imposing WAR on single-epoch PPP solutions. Specifically, most reduction rates are more than 45%. In contrast, Europe stations can only observe about 10 satellites and the RMS reduction rates decline to 30–40%. The worst performance comes to American stations over which only eight satellites can be tracked on average. This poor satellite visibility results in less than 20% of RMS improvement at some stations. Therefore, Fig. 7 reinforces that the positioning accuracy of instantaneous PPP-WAR improves with the increasing number of visible triple-frequency satellites.

4.4 Instantaneous PPP-WAR on a mobile vehicle

In addition to the instantaneous PPP-WAR tests at static stations, we collected triple-frequency multi-GNSS observations using a vehicle moving along urban streets (Fig. 3). Since there were a tunnel and two crossovers along the route, the satellite signals were totally interrupted three times per lap, which are numbered as \(\textcircled {1}\), \(\textcircled {2}\) and \(\textcircled {3}\) in both the main panel and the inset of Fig. 3. We can see that the number of visible satellites was normally around 12, but was decreased dramatically to 5–7 during the signal interruptions. Figure 8 shows the 1-Hz position estimates of both instantaneous PPP-WAR and single-epoch PPP. Again, even in case of a mobile platform in a complex urban environment, instantaneous PPP-WAR outperforms single-epoch PPP at almost all epochs of the hour. After removing the outlier solutions whose position errors exceed 3 m in either horizontal direction, we hold the remaining 99.31% of epochs, of which the RMS of position errors is 0.29, 0.35 and 0.77 m in the east, north and up components for instantaneous PPP-WAR, respectively, as opposed to 0.50, 0.69 and 1.56 m for single-epoch PPP; these statistics hence suggest a 50% improvement in all three directions after WAR imposed on single-epoch PPP. In particular, smaller than 0.3 m positioning errors in the horizontal directions (see the dashed green lines in Fig. 8) are achieved at 41% of all epochs of instantaneous PPP-WAR solutions, while only 15% for single-epoch PPP. As a typical example, Fig. 9a shows a snapshot of the vehicle trajectory near area \(\textcircled {4}\) in Fig. 3. It can be seen that the instantaneous PPP-WAR solutions (blue lines) coincide well with the truth benchmarks (yellow lines); PPP-WAR solutions identify the road lanes clearly with minimal deviations. On the contrary, the single-epoch PPP solutions (red lines) have often pronounced excursions of up to 1 m from the benchmarks along all laps. We therefore demonstrate that instantaneous PPP-WAR has the potential to maintain decimeter-level positioning accuracy in the horizontal plane even in urban areas with the goal of sensing traffic conditions.

Fig. 8
figure 8

Positioning errors (meter) of instantaneous PPP-WAR and single-epoch PPP for the east, north and up components on a moving vehicle over a duration of about 1 h on April 17, 2018. The number of visible satellites and the PDOP values refer to the inset of Fig. 3. The epochs when the vehicle was passing the tunnel and the two crossovers are marked using the same numbers shown in Fig. 3 (i.e., “\(\textcircled {1}\)”, “\(\textcircled {2}\)” and “\(\textcircled {3}\)”). RMS of the epoch-wise position differences from benchmark solutions is presented at the bottom of each panel. The dashed green horizontal lines in the top and middle panels denote a range of ± 0.3 m whereas those in the bottom panel denote ± 0.5 m

Full size image

Nevertheless, more complex urban environment will challenge instantaneous PPP-WAR. Figure 3 shows three overhead structures labeled in numbers \(\textcircled {1}\), \(\textcircled {2}\) and \(\textcircled {3}\) (one tunnel and two crossovers) which blocked satellite signals. Rapid degradations of positioning accuracy on those occasions are evidenced by the spikes also labeled in numbers \(\textcircled {1}\), \(\textcircled {2}\) and \(\textcircled {3}\) in Fig. 8; an error of up to several meters can be caused for the horizontal components. Figure 9b hence presents a representative snapshot of the vehicle trajectory after the passage of crossover 1 labeled as number \(\textcircled {2}\) in Fig. 3. The dots on the yellow lines show that the benchmark solutions were correctly anchored on the road immediately after the crossing. In contrast, both instantaneous PPP-WAR and single-epoch PPP missed several epochs of solutions during the recovery from the crossover blockage. A close look at the vehicle-borne GNSS observations exposes that there were few satellites (< 6) or only single-frequency data when the vehicle escaped from the shading of those overhead structures, hence greatly limiting the functioning of instantaneous PPP-WAR. This difficult condition for instantaneous PPP-WAR makes short-baseline solutions more trustworthy, the truth benchmark of this study. Therefore, we have to keep in mind that only on the premise of sufficient number of multi-frequency observations can instantaneous PPP-WAR work efficiently and flexibly.

Fig. 9
figure 9

Snapshots of vehicle trajectory overlaid on Google map. The yellow, blue and red lines denote the solutions of truth benchmark, instantaneous PPP-WAR and single-epoch PPP, respectively. The color-coded dots on the lines represent the epochs where a positioning solution is achieved, no matter whether correct or not. Note that a and b correspond to scenes \(\textcircled {4}\) and \(\textcircled {2}\) in the main panel of Fig. 3, respectively. There is a crossover at the bottom of b

Full size image
Fig. 10
figure 10

Mean ratio values in (extra-)wide-lane ambiguity validation against the number of resolved ambiguities. The statistics are computed over all resolved epochs at all 107 stations in Fig. 2

Full size image

5 Discussions on high-dimensional ambiguity resolution

Table 2 and Fig. 7 demonstrate that the more satellites contribute to instantaneous PPP-WAR, the better positioning accuracy we can achieve. For example, a 20 cm horizontal position accuracy, preferable to autonomous driving, is achieved in case of over 15 satellites. However, too many satellites per epoch will jeopardize both fast ambiguity search and reliable ambiguity validation (Verhagen et al. 2012). To be specific, the search for the integer candidates will slow down or even get stuck on the occasion of several tens of ambiguities injected simultaneously into LAMBDA (e.g., Jazaeri et al. 2012; Lu et al. 2018); even if smoothly through LAMBDA, the integer candidate validation for high-dimensional ambiguities through the ratio tests often malfunctions due to the hard choice of threshold values. Figure 10 shows the mean ratio values over the 31 days at all 107 stations against the number of resolved ambiguities. We can see that the ratio values for both extra-wide-lane and wide-lane ambiguity resolution are decreased with respect to the increasing number of resolved ambiguities per epoch. Although the ratio values for extra-wide-lane ambiguity resolution remain far larger than 2 in case of 21 ambiguities, those for wide-lane ambiguity resolution are only marginally over 2, the pre-defined threshold for the ratio tests in this study. In fact, we did come across a small portion (3.2%) of epochs with wide-lane ratio values below 2; however, we still “recklessly” fixed the wide-lane ambiguities to integers. As a result, about 37% of these epochs were not resolved correctly. One remedy effort is that the ratio test should be built upon a fixed failure rate rather than a fixed critical threshold (Teunissen and Verhagen 2009). Another solution is that an optimum subset of ambiguities is identified first for the LAMBDA search and ratio test, whereas the remainder are fixed afterward once the subset is resolved successfully (e.g., Wang and Feng 2013).

6 Conclusions and outlook

We developed a method aiming at global instantaneous decimeter-level positioning by tightly coupling GPS/BeiDou/Galileo/QZSS triple-frequency observations. Station ISPBs and satellite FCBs were computed at the server end to facilitate inter-GNSS ambiguity resolution at a single station; with these augmentation products, extra-wide-lane and wide-lane ambiguities could be resolved using a single epoch of data by PPP users (i.e., “instantaneous PPP-WAR” in short).

To validate this method, we first used 31 days of data from 107 globally distributed static stations. The station-specific daily extra-wide-lane and wide-lane ISPBs were computed with high precisions of 0.04 and 0.11 cycles, respectively. Extra-wide-lane ISPBs changed minimally from day to day with over 95% of variations falling in ± 0.1 cycles, while over 83% within ± 0.1 cycles for wide-lane ISPBs. Similarly, satellite-specific daily inter-system FCBs achieved a high precision of better than 0.05 cycles; over 98% of day-to-day extra-wide-lane FCB variations fell in ± 0.1 cycles, while over 83% within ± 0.1 cycles for wide-lane FCBs. The high stability of both ISPB and FCB products over a couple of days favored their precise prediction for real-time PPP-WAR. With the ISPB and FCB products, we could instantly achieve extra-wide-lane ambiguity-fixed solutions at almost all epochs, and 91.2% of epochs could have all or a maximum subset of their wide-lane ambiguities resolved reliably. We envision that this percentage can be further increased in case of full multi-frequency GNSS constellations.

On instantaneous PPP-WAR positioning accuracy, 0.22 m, 0.18 m and 0.63 m for the east, north and up components, respectively, could be attained when the satellite number exceeded 15. Even in America when most triple-frequency signals came from a limited number of GPS and Galileo satellites (6–8 usually), we were still able to achieve a positioning accuracy of better than 0.5 m in the horizontal directions. In addition, a vehicle-borne PPP-WAR test lasting about 60 min in an urban area was carried out with on average 12 triple-frequency satellites in view. We achieved eligible PPP-WAR solutions at 99.31% of all epochs, and the RMS of positioning differences from truth benchmarks was 0.29, 0.35 and 0.77 m for the east, north and up components, respectively, which improved the identification of road lanes.

In this study, we always carried out single-epoch solutions to highlight the instantaneity of decimeter-level positions for the horizontal component on a global scale. However, we should keep in mind that continuous carrier-phase observations, which are obtainable in most open and semi-open sky-view conditions, can be exploited to smooth out the decimeter-level position errors to better facilitate autonomous driving and other high-precision time-critical applications (e.g., Li et al. 2017). In addition, the integration of PPP-WAR with inertial sensors will also improve the position availability in case of the early recovery from GNSS signal blockages.