1 Introduction

In this paper, we investigate the combination of a noisy satellite-only global gravity model (GGM) with noisy high-resolution datasets (e.g. terrestrial gravity anomalies) to estimate a local quasi-geoid model using weighted least-squares techniques. By considering the satellite-only GGM as one of the noisy datasets, we expect to improve the quality of the estimated local quasi-geoid model. By exploiting existing information about the noise variances and covariances in combination with weighted least-squares techniques, we aim at making a step forward towards a comprehensive description of the quality of the estimated quasi-geoid model in terms of a full noise covariance matrix for quality control and further data processing.

The problem is timely. The quality and spatial resolution of the most recent satellite-only GGMs, which are mainly based on data of the Gravity Recovery and Climate Experiment (GRACE) and Gravity field and steady-state Ocean Circulation Explorer (GOCE) satellite missions, have improved dramatically compared to pre-mission models. Moreover, the GGM’s spherical harmonic coefficients are now complemented with a full noise covariance matrix. For models such as GOCO05s (Mayer-Gürr et al. 2015), the quality of the noise covariance matrix benefits from (i) a post-fit residual analysis, which provides more realistic models of the data noise (e.g. Farahani et al. 2013), and (ii) numerically efficient algorithms to propagate the full data noise covariance matrices into the noise covariance matrix of the estimated spherical harmonic coefficients (e.g. Farahani et al. 2013). Some progress has also been made regarding high-resolution datasets frequently used in local quasi-geoid modelling. An example is Farahani et al. (2017) who derived coloured noise models for radar altimeter-based along-track quasi-geoid height differences, or Slobbe (2013) who successfully accounted for long-wavelength errors in terrestrial gravity anomalies (e.g. Heck 1990) by augmenting the functional model with additional parameters.

Until now, a GGM with full noise covariance matrix has not been used as one of the noisy datasets in the computation of a local quasi-geoid model. The standard approach is remove–compute–restore approach, i.e. the GGM is used to facilitate a local approach to quasi-geoid modelling by removing most of the energy in the data at the long wavelengths. From a theoretical point of view, the combination of a local set of terrestrial gravity anomalies with a noisy GGM has been considered in a number of publications since the 1980s. They all use a modification of Stokes’ formula and go back to the early work of Sjöberg and Wenzel (Sjöberg 1980, 1981; Wenzel 1981). At that time, only error degree variances of the GGM were used. The modification of Stokes’ kernel was formulated as a global optimization problem, in which either the variance or the mean square error of the quasi-geoid heights was minimized. Since then, the stochastic spectral combination methods were applied routinely when computing local quasi-geoid models. An example is the European quasi-geoid EGG08 (Denker et al. 2008; Denker 2013), which uses the spectral combination method of Wenzel (1981). Sjöberg (2005) was the first who derived the formalism of a local least-squares modification of Stokes’ formula, which uses, among others, the full noise covariance matrix of the GGM to compute the weights per spherical harmonic degree. In (Sjöberg 2011), the restriction to weights per spherical harmonic degree was given up. To our knowledge, this method has not been investigated yet in detail. Some numerical aspects were studied in Ågren (2004) and Ellmann (2004), in particular numerical instabilities when estimating the spectral weights, which naturally arise in local applications.

Here we follow another approach to local quasi-geoid modelling, which uses least-squares techniques to estimate the parameters of a local spherical radial basis function (SRBF) model of the disturbing potential from the available datasets. Least-squares techniques have many advantages. In particular, they allow us to include noise covariance matrices, improve them using variance component estimation, provide variance–covariance information about the estimated parameters and linear functionals of them, and allow the use of statistical hypothesis testing to test the validity of the mathematical model. Least-squares local quasi-geoid modelling using SRBFs has been intensively studied by various authors, see Klees et al. (2008) for a literature overview until 2007. Since then, a number of studies investigated various aspects of the use of SRBFs in local quasi-geoid modelling. This comprises the choice of the type of SRBFs (e.g. Tenzer and Klees 2008; Bentel et al. 2013a, b), SRBF network design and numerical optimization (e.g. Wittwer 2009), regularization issues (e.g. Naeimi 2013), and the optimization of the location of the SRBFs (e.g. Lin et al. 2014). Some aspects related to the combination of data with different bandwidths have been discussed in Panet et al. (2011); Naeimi (2013); Bentel and Schmidt (2016); Lieb et al. (2016); Lieb (2017). However, they do not cover numerical studies about the combination of a GGM with full noise covariance matrix with high-resolution noisy datasets.

An alternative to the use of a GGM as one of the noisy datasets in local quasi-geoid modelling is to complement the high-resolution local datasets with the original satellite data at altitude, e.g. satellite gravity gradients from the GOCE mission, low–low satellite-to-satellite tracking data from the GRACE mission, and high–low satellite-to-satellite tracking data from GRACE, GOCE, and other low Earth orbiters. Examples in the context of local quasi-geoid modelling with SRBFs are Lieb et al. (2015) and Lieb (2017). The major drawback of this approach is the complexity of the functional model for the low–low satellite-to-satellite tracking data and the huge amount of data. This may be the reason why numerical studies published so far (e.g. Lieb 2017) do not use high–low satellite-to-satellite tracking data, limit to a subset of the available GOCE data (e.g. the second radial derivative of the gravitational potential), or use GRACE-based along-track gravity potential differences as pseudo-observations instead of the original K-band ranging data, often in combination with simplified noise models. Overall, this approach does not offer a significant advantage compared to the use of a GGM that is based on the same data and, therefore, is not pursued in this study.

The study addresses to main research questions: (i) What is a suitable functional model for the satellite-only GGM? (ii) How to combine the satellite-only GGM with high-resolution datasets to obtain a quasi-geoid model that optimally exploits the information content in all datasets?

The remainder of this paper is organized as follows. First, we introduce local single-scale and two-scale SRBF models of the disturbing potential and suggest three functional models to be used in a least-squares estimation of the quasi-geoid model from the satellite-only GGM and the high-resolution datasets. Following this, we describe the set-up of the numerical experiments, which were designed to investigate the performance of the SRBF models and the functional models. Thereafter, we present and discuss the results of the numerical experiments. We conclude by emphasizing the main findings and identifying topics for future research.

2 Parameterization and functional models

2.1 Local parameterization of the disturbing potential

A prerequisite for local gravity field modelling is that the involved datasets do not contain much long-wavelength energy, where “long” relates to the size of the data area. One possibility to achieve this is by reducing all datasets for the contribution of a global model of the disturbing potential. Then, the disturbing potential to be parameterized in local modelling is a residual quantity with little, though nonzero energy at the long wavelengths. Moreover, there is an upper limit of the highest attainable spatial resolution, which depends on the data distribution and signal-to-noise ratio. This allows us to consider a local model of the disturbing potential which is band-limited to some maximum degree, say \(L_{\tiny \text{ max }}\). From now on, we call this residual and band-limited disturbing potential simply “disturbing potential”, denoted T.

In this study, we use SRBFs to model T over an area of interest. Basically, two models will be used. The first one is a single-scale model, i.e.

$$\begin{aligned} T(x) = \sum _{i=1}^I c_i\,\varPhi (x,z_i), \end{aligned}$$
(1)

where

$$\begin{aligned} \varPhi (x,z_i)= & {} {R \over |x|}\,\sum _{l=0}^{L_{\tiny \text{ max }}}\, \phi _l\,\Big ({|z_i| \over |x|}\Big )^l\,Q_l(\hat{x} \cdot \hat{z}_i),\quad \; \nonumber \\&x \in \overline{\text{ ext } \sigma _R}, \; z_i \in \text{ int } \sigma _R, \end{aligned}$$
(2)

is a SRBF located at \(z_i\), \(\{c_i\}\) are the SRBF coefficients, which are to be estimated from the data using least-squares techniques, \(Q_l\) is the reproducing kernel of the space of harmonic functions of degree l, \(\phi _l\) is the Legendre coefficient of degree l, \(\hat{x}\) and \(\hat{z}_i\) are points on the unit sphere, and \(\sigma _R\) is the surface of a sphere of radius R. The model of Eq. (1) is referred to as a single-scale model.

Alternatively, we may use a multi-scale model involving several sets of SRBFs representing different scales, i.e.

$$\begin{aligned} T(x) = \sum _{j=1}^J \sum _{i=1}^{I_j} c_{j i}\,\varPsi _j(x,z_{j i}), \end{aligned}$$
(3)

where j indicates the scale, \(\{c_{j \cdot }\}\) are the SRBF coefficients at scale j, and \(\varPsi _j(\cdot ,z_{ji})\) is a SRBF of scale j centred at the point \(z_{ji}\). In the context of a multi-scale analysis, the SRBF \(\varPsi _j\) may be defined as (e.g. Lieb 2017)

$$\begin{aligned}&\varPsi _j(x,z_{ji})\nonumber \\&\quad = {\left\{ \begin{array}{ll} {R \over |x|}\, \sum _{l=0}^{l_1} \phi _l^{(1)}\,\Big ({|z_{1i}| \over |x|}\Big )^l\,Q_l(\hat{x} \cdot \hat{z}_{1i}) &{} \text {for }j=1 \\ {R \over |x|}\,\sum _{l=0}^{l_j} (\phi _l^{(j)} - \phi _l^{(j-1)})\,\Big ({|z_{ji}| \over |x|}\Big )^l\,Q_l(\hat{x} \cdot \hat{z}_{ji}) &{} \text {for }j=2 \ldots J. \end{array}\right. } \nonumber \\ \end{aligned}$$
(4)

Frequently, the relation \(l_j = 2^j-1\) is used to relate the scale index j to the maximum spherical harmonic degree \(l_j\), which is resolved at scale j, though other choices are possible.

2.2 Functional models

In the framework of this study, we assume that there are basically two datasets, i.e. a low-resolution dataset and a high-resolution dataset. The low-resolution dataset \(d_1\) is synthesized from the spherical harmonic coefficients of the GGM as

$$\begin{aligned} d_1(x_{1k})= & {} \sum _{n=0}^{L_1} \sum _{m=1}^{2n+1} \Big (\hat{c}_{nm} - c_{nm}^{(\tiny {\text{ ref }})}\Big )\, (F_1\, H_{nm})(x_{1k}),\quad \nonumber \\&k=1 \ldots K_1, \end{aligned}$$
(5)

where \(\{\hat{c}_{nm}\}\) are the spherical harmonic coefficients of the GGM, \(\{c_{nm}^{(\tiny {\text{ ref }})}\}\) are the spherical harmonic coefficients of the reference GGM, and \(H_{nm}\) is a solid spherical harmonic of degree n. The low-resolution dataset is band-limited to a degree \(L_1 \le L_{\tiny \text{ GGM }}\), where \(L_{\tiny \text{ GGM }}\) is the maximum degree of the GGM. We assume that the high-resolution dataset \(\{d_2(x_{2k}): k=1 \ldots K_2\}\) allows the resolution of wavelengths up to a maximum degree \(L_2 \le L_{\tiny \text{ max }}\), where \(L_2\) depends on the point density and the signal-to-noise ratio. Defining a kernel

$$\begin{aligned} \delta _L(x,y)= & {} \sum _{n=0}^L {1 \over 4\pi R^2}\Big ({R \over |x|}\Big )^{n+1}\Big ({R \over |y|}\Big )^{n+1}\,Q_n(\hat{x} \cdot \hat{y}),\quad \nonumber \\&x,\,y \in \overline{\text{ ext } \sigma _R}, \end{aligned}$$
(6)

a spherical convolution of T with \(\delta _L\) as

$$\begin{aligned} (\delta _L * T)(x) = \int _{\sigma _R} \delta _L(x,y) T(y)\,d\sigma _R(y), \end{aligned}$$
(7)

and linear functionals \(F_1\) and \(F_2\) of the disturbing potential T, we may relate the datasets \(d_1\) and \(d_2\) to the disturbing potential T as

$$\begin{aligned} E\{d_1\}(x_{1k})&= \left( F_1 (\delta _{L_1} * T)\right) (x_{1k}), \quad k=1 \ldots K_1, \end{aligned}$$
(8)
$$\begin{aligned} E\{d_2\}(x_{2k})&= \left( F_2 (\delta _{L_2} * T)\right) (x_{2k}),\quad k=1 \ldots K_2, \end{aligned}$$
(9)

where \(E\{\cdot \}\) denotes mathematical expectation. We will investigate three functional models to estimate a local quasi-geoid model by least squares from the low-resolution dataset \(d_1\) and the high-resolution dataset \(d_2\).

Functional model no. 1 uses the single-scale model of the disturbing potential, Eq. (1), and reads:

$$\begin{aligned} E\{d_1\}(x_{1k})&\!=\! \sum _{i=1}^I c_i \left( F_1 (\delta _{L_1} *\varPhi )\right) (x_{1k},z_i),\, k=1 \ldots K_1, \end{aligned}$$
(10)
$$\begin{aligned} E\{d_2\}(x_{2k})&\!=\! \sum _{i=1}^I c_i\,\left( F_2 (\delta _{L_2} * \varPhi )\right) (x_{2k},z_i),\, k=1 \ldots K_2. \end{aligned}$$
(11)

The coefficients \(\{c_i\}\) are estimated simultaneously from the two noisy datasets using weighted least-squares techniques. The weight matrix of each dataset is the inverse of the noise cofactor matrix.

Functional model no. 2 uses the single-scale model of the disturbing potential, Eq. (1), and reads

$$\begin{aligned}&(P * E\{d_1\})(x_{1k}) \!=\! \sum _{i=1}^I c_i \left( F_1 (P * \varPhi )\right) (x_{1k},z_i),\, k\!=\!1 \ldots K_1, \nonumber \\\end{aligned}$$
(12)
$$\begin{aligned}&E\{d_2\}(x_{2k}) = \sum _{i=1}^I c_i\,\left( F_2 (\delta _{L_2}* \varPhi )\right) (x_{2k},z_i),\quad k = 1 \ldots K_2. \end{aligned}$$
(13)

The kernel P of Eq. (12) is defined as

$$\begin{aligned} P(x,y)= & {} \sum _{n=0}^\infty {1 \over 4\pi R^2}\Big ({R \over |x|}\Big )^{n+1}\Big ({R \over |y|}\Big )^{n+1}\,\nonumber \\&h_n\, Q_n(\hat{x} \cdot \hat{y}),\quad x,\,y \in \overline{\text{ ext } \sigma _R} . \end{aligned}$$
(14)

The Legendre coefficients \(\{h_n: n = 1,2,\ldots \}\) are equal to 1 for degrees \(n \le p_1\), taper off between degrees \(p_1< n < p_2\), and are zero for all degrees \(n \ge p_2\). An example is a cosine taper,

$$\begin{aligned} h_n = {\left\{ \begin{array}{ll} 1, &{} n < p_1 \\ 0.5 + 0.5 \cos \Big ( \pi {n - p_1 \over p_2 - p_1} \Big ), &{} p_1 \le n \le p_2 \le L_2 \\ 0, &{} n > p_2 \end{array}\right. }. \nonumber \\ \end{aligned}$$
(15)

This taper will be used in the numerical experiments of Sect. 3. The coefficients \(\{c_i\}\) are estimated simultaneously from the two noisy datasets using weighted least-squares techniques. The weight matrix of each dataset is proportional to the inverse of the noise covariance matrix. The noise covariance matrix of \(P*d_1\) is computed from the full noise covariance matrix of \(d_1\) using the law of covariance propagation.

The difference between the functional models no. 1 and no. 2 is in the functional model of the low-resolution dataset. Functional model no. 2 uses a tapered SRBF, whereas functional model no. 1 uses a truncated SRBF. Moreover, functional model no. 2 applies the same taper to the dataset, whereas functional model no. 1 uses the original dataset.

Functional model no. 3 uses a two-scale model of the disturbing potential, i.e. Eq. (3) with \(J=2\):

$$\begin{aligned} T(x) = \sum _{i=1}^{I_1} c_{1i}\,\varPsi _1(x,z_{1i}) + \sum _{i=1}^{I_2} c_{2i}\,\varPsi _2(x,z_{2i}). \end{aligned}$$
(16)

The first term on the right-hand side is a low-resolution model of T comprising degrees from 0 to \(L_1\), i.e. its resolution is identical to the resolution of dataset \(d_1\). The second term on the right-hand side complements the low-resolution model to the maximum resolution \(L_2\) of dataset \(d_2\). In the context of a multi-resolution analysis, it represents a detail space comprising wavelengths from degrees \(L_1+1\) to \(L_2\).

The basis functions \(\varPsi _1\) and \(\varPsi _2\) of Eq. (16) are defined as

$$\begin{aligned} \varPsi _1(x,z)&= (P* \varPhi )(x,z), \end{aligned}$$
(17)
$$\begin{aligned} \varPsi _2(x,z)&= \left( (\delta _{L_2} - P) * \varPhi \right) (x,z), \end{aligned}$$
(18)

with \(\varPhi (x,z)\) of Eq. (2). Inserting the last two equations into Eq. (16), the two-scale model of the disturbing potential T is written as

$$\begin{aligned} T(x)= & {} \sum _{i=1}^{I_1} c_{1i}\,(P*\varPhi )(x,z_{1i}) \nonumber \\&+ \sum _{i=1}^{I_2} c_{2i}\,\left( (\delta _{L_2}-P)*\varPhi \right) (x,z_{2i}), \end{aligned}$$
(19)

with \(\varPhi \) of Eq. (2). The coefficients \(\{c_{1i}\}\) and \(\{c_{2i}\}\) are estimated in two steps. First, we use the functional model

$$\begin{aligned} E\{d_2\}(x_{2k}) =\! \sum _{i=1}^{I_2} c_{2i} \left( F_2 (\delta _{L_2} *\varPhi )\right) (x_{2k},z_{2i}), \, k=1 \ldots K_2, \nonumber \\ \end{aligned}$$
(20)

and estimate the coefficients \(\{c_{2i}\}\) using weighted least squares. Then, we define a new dataset

$$\begin{aligned} d_3(x_{1k}) := \sum _{i=1}^{I_1} \hat{c}_{2i}\,(F_1 \varPsi _1)(x_{1k},z_{1i}),\quad k=1 \ldots K_1, \end{aligned}$$
(21)

where \(\{\hat{c}_{2i}\}\) denotes the least-squares estimate of \(\{c_{2i}\}\). The resolution of the dataset \(d_3\) is identical to the resolution of the dataset \(P * d_1\). In that sense, \(d_3\) and \(P*d_1\) are spectrally consistent. Then, we use the functional model

$$\begin{aligned}&\begin{pmatrix} (P*E\{d_1\})(x_{1k}) \\ E\{d_3\}(x_{1k}) \end{pmatrix} = \sum _{i=1}^{I_1} c_{1i}\, (F_1 \varPsi _1)(x_{1k},z_{1i}) \nonumber \\&\quad = \sum _{i=1}^{I_1} c_{1i}\, \left( F_1 (P*\varPhi )\right) (x_{1k},z_{1i}),\quad k=1 \ldots K_1, \end{aligned}$$
(22)

and compute an estimate \(\{\hat{c}_{1i}\}\) of the coefficients \(\{c_{1i}\}\), using weighted least-squares techniques. The noise covariance matrix of dataset \(d_3\) is computed from the noise covariance matrix of the estimated coefficients \(\{\hat{c}_{2i}\}\) using the law of covariance propagation. It is a full matrix. The least-squares estimate of the disturbing potential is then given by Eq. (19), with \(\{c_{1i}\}\) and \(\{c_{2i}\}\) replaced by the estimates \(\{\hat{c}_{1i}\}\) and \(\{\hat{c}_{2i}\}\), respectively.

Remarks

  1. 1.

    The motivation of using the functional model of Eq. (10) is the following. Dataset \(d_1\) and its full noise covariance matrix are band-limited to a degree \(L_1 \le L_{\tiny \text{ GGM }}\). Therefore, the right-hand side of the functional model must also be band-limited to the same degree. To achieve this, we consider the signal \(1 \cdot \varPhi \), with \(\varPhi \) of Eq. (2). We expand this signal on the sphere \(\sigma _R\) in spherical harmonics and truncate the expansion at degree \(L_1\). The result is identical to \(\delta _{L_1} * \varPhi \). If the right-hand side of the functional model would not be band-limited to degree \(L_1\), the least-squares estimate of the coefficients \(\{c_{1i}\}\) would be biased towards zero for the wavelengths above degree \(L_1\). This is due to the fact that a band-limited noise covariance matrix is equivalent to zero noise and noise correlations for degrees above \(L_1\).

  2. 2.

    The motivation to use the functional model of Eq. (12) is the result of numerical experiments which are described in Sect. 3 and discussed in Sect. 4. There, we will show that \(|d_1(\cdot ) - \sum _{i=1}^{I_1} c_i\,\left( F_1 (\delta _{L_1} * \varPhi )\right) (\cdot ,z_i)|\) is much larger than the noise in the dataset \(d_1\), i.e. the functional model of Eq. (10) is not accurate enough. Compared to this, the error of the functional model of Eq. (12) can be made much smaller than the data noise standard deviation if P of Eq. (14) is chosen as in Eq. (15).

  3. 3.

    The functional model of Eqs. (20), (22) is different from the model suggested in  Lieb (2017), which in our notation is

    $$\begin{aligned} E\{d_1\}( \cdot )&= \sum _{i=1}^{I_1} c_{1i}\,\left( F_1 (\delta _{L_1} * \varPhi )\right) (\cdot ,z_{1i}), \end{aligned}$$
    (23)
    $$\begin{aligned} E\{d_2\}(\cdot )&= \sum _{i=1}^{I_2} c_{1i}\, \left( F_2 (\delta _{L_1} * \varPhi )\right) (\cdot ,z_{1i}) \nonumber \\&\quad +\, \sum _{i=1}^{I_2} c_{2i}\,\left( F_2 \big ( (\delta _{L_2} - \delta _{L_1})*\varPhi \big )\right) (\cdot ,z_{2i}). \end{aligned}$$
    (24)

    Moreover, Lieb (2017) suggests to estimate the coefficients \(\{c_{1i}\}\) and \(\{c_{2i}\}\) simultaneously using weighted least-squares techniques. Some preliminary experiments with this model and \(\varPhi \) set equal to the Abel–Poisson kernel (Freeden et al. 1998) point to a sub-optimal quality of the estimated quasi-geoid model at the resolution of the dataset \(d_1\), which is likely caused by the simultaneous estimation of the two sets of coefficients \(\{c_{1i}\}\) and \(\{c_{2i}\}\). However, additional numerical experiments are necessary to support these preliminary results. They are out of the scope of this study.

3 Numerical experiments

The parameterizations and functional models of Sect. 2 will be analysed using numerical experiments. Though from a practical point of view, working with real data may be desired, we decide to use a state-of-the-art combined GGM and a satellite-only GGM to generate the (noise-free) high-resolution and low-resolution datasets, respectively. The main motivation for us to prefer GGMs to real datasets is that some problems and limitations of the functional models of Sect. 2.2 would be masked by deficiencies in real datasets, e.g. unmodelled signal and noise and data gaps. This would make a proper interpretation of the results impossible. Generating the exact data from GGMs and adding noise which is consistent with the corresponding noise covariance matrix provides a complete error control and facilitates a proper interpretation of the results.

Table 1 Experimental set-ups used in Sect. 4
Full size table

The datasets are generated from the GGMs using a spherical harmonic synthesis and thereafter reduced for the contribution of a long-wavelength GGM, which serves as the reference model. Here we use EIGEN-6C4 (Förste et al. 2014) to generate the (noise-free) high-resolution dataset and the regularized version of GOCO05s (Mayer-Gürr et al. 2015) to generate the (noise-free) low-resolution dataset. The latter is also used as the reference model, though up to a smaller maximum degree. The low-resolution dataset consists of a set of height anomalies. This is a logic choice as the target quantity is a quasi-geoid model. The noise covariance matrix of the low-resolution dataset is obtained from the full noise covariance matrix of the spherical harmonic coefficients of the unregularized version of GOCO05s by applying the law of covariance propagation. A logic choice for the high-resolution dataset would be gravity anomalies. Here, we use gravity disturbances for simplicity reasons. Noise in gravity disturbances is zero-mean white Gaussian, i.e. the noise covariance matrix of the high-resolution dataset is a scaled unit matrix. More details about the datasets are provided in Table 1.

The datasets are generated at the Earth’s surface and cover an area, which is referred to as “the data area”. The Earth’s surface is represented by the digital elevation model EuroDEM v1.0 (Hovenbitzer 2008) with \(2''\) grid width. In areas where this model is not available, we use SRTM version 2.1 (Farr et al. 2007) with \(3''\) grid width. For the remaining areas, we use ASTER GDEM v2 (Tachikawa et al. 2011) with \(1''\) grid width.

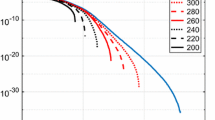
The SRBF of Eq. (2) is a Poisson wavelet of order 3 (Holschneider and Iglewska-Nowak 2007). Different from the Shannon kernel, which is frequently used in local quasi-geoid modelling, the Legendre spectrum of a Poisson wavelet relative to a sphere of radius R has a peak at degree \({3R \over R - |z|}\), where \(z < R\) is the location of the Poisson wavelet (cf. Fig 1). The Legendre spectrum of a Poisson wavelet may give the impression that a single-scale Poisson wavelet model is not able to accurately represent a quasi-geoid with a resolution one typically encounters in practice. Therefore, Chambodut et al. (2005) suggest to use Poisson wavelets of different scales to guarantee that the space of spherical harmonic complete to a degree \(L_2\) is sufficiently well covered. However, Slobbe (2013) successfully used a single-scale Poisson wavelet model to compute a quasi-geoid model for the Netherlands mainland, continental shelf, and Wadden Islands with an accuracy of about 1.5 cm standard deviation using real data. The only prerequisite is that the energy in the data at the lowest and highest frequencies is reduced by using a reference GGM and a digital terrain model, respectively. The Poisson wavelets are located at a constant depth below the Earth’s surface and cover the data area. Their horizontal positions correspond to the points of a Fibonacci grid (Gonzalez 2010).

Fig. 1
figure 1

Normalized Legendre spectrum of Poisson wavelets of order 3 at a depth of (from right to left) 20, 40, 80, 160, and 320 km, respectively. Note the logarithmic scale of the horizontal axis

Full size image

Whenever a new set of Poisson wavelets is chosen in the numerical experiments, we have to determine the optimal depth and the optimal mean distance between the Poisson wavelets. This is done using noise-free datasets generated from the corresponding GGMs on grids dense enough to preserve the information content in the GGM. We define a set of candidate depths and candidate mean distances, and estimate the model coefficients by least squares using the corresponding dataset (i.e. gravity disturbances when looking for a high-resolution model and height anomalies when looking for a low-resolution model). The depth and mean distance that provide the model with the smallest RMS difference to a height anomaly control dataset are selected. The fit of this model to the control dataset is referred to as the “parameterization error”. Note that the parameterization error is always defined in terms of height anomalies, no matter whether the dataset comprises gravity disturbances or height anomalies. Other control datasets are generated to assess the quality of the estimated quasi-geoid models in Sect. 4. They always comprise height anomalies on grids different from the data grids and are computed using a spherical harmonic synthesis of the GGMs from which the noise-free datasets were generated.

When computing quasi-geoid models using weighted least-squares techniques, we calculate the normal equations explicitly and apply Tikhonov regularization (Tikhonov 1963) with a unit regularization matrix. The regularization parameter is fixed using the method in (Wittwer 2009). The normal equations are solved using a parallelized QR-decomposition with column pivoting. This solver is preferred to a Cholesky decomposition due to its much better stability for ill-conditioned linear systems at the benefit of a smaller bias in the least-squares estimate due to a smaller regularization parameter.

Table 1 summarizes the set-up of the numerical experiments, which will be used in Sect. 4.

4 Results

4.1 Functional model no. 1

We use experimental set-up no. 1 of Table 1. Table 2 shows some statistics of the least-squares residuals for the estimated quasi-geoid model. The standard deviation (SD) of the residuals is 9.86 cm for the low-resolution dataset and 2.02 mGal for the high-resolution dataset. The latter corresponds to the standard deviation of the noise in the high-resolution dataset. The former, however, is much larger than the noise. From this we conclude that the estimated quasi-geoid model fits the high-resolution dataset within noise, but gives a poor fit to the low-resolution dataset.

Table 2 Statistics of the least-squares residuals using functional model no. 1 of Sect. 2.2
Full size table

Table 3 shows the statistics of the errors in the estimated quasi-geoid model. They are computed over the area of interest.

Table 3 Error statistics (in units of cm) of the quasi-geoid model which has been estimated using the functional model no. 1 of Sect. 2.2
Full size table

The errors range from \(-10.68\) to 12.76 cm; the error SD is 3.46 cm. After applying a low-pass filter at the cut-off degree 200, the estimated quasi-geoid model error SD is 7.62 and 7.68 cm depending on what low-resolution signal is taken as the reference.

To get more insight into the reason why the estimated quasi-geoid model does not fit the low-resolution dataset within noise, we repeat the experiment with noise-free data. The error SD of the estimated quasi-geoid model reduces from 3.46 to 0.09 cm. This is identical to the SD of the parameterization error. Hence, when using noise-free data, the estimated quasi-geoid model perfectly fits the high-resolution dataset. This does not apply, however, to the low-pass-filtered quasi-geoid model; the error SD is 7.12 and 7.46 cm, respectively, i.e. comparable to the results using noisy data. Hence, the poor fit of the estimated quasi-geoid model to the low-resolution dataset cannot be explained by the noise in this dataset. Additional numerical experiments (not shown here) reveal that the fit to the low-resolution dataset can only be improved by further increasing the size of the data area. The \(5^\circ \) extension beyond the area of interest in all directions as used here is already a challenge in real quasi-geoid modelling as access to data of neighbouring countries is not guaranteed. Moreover, we found that the fit to the low-resolution dataset improves slowly when enlarging the data area. From this we conclude that the poor fit of the estimated quasi-geoid model to the low-resolution dataset is caused by the hard truncation of the Poisson wavelets. This introduces strong spatial-domain oscillations, which are cut off at the border of the data area when computing the elements of the design matrix. This introduces errors in the functional model, which exceed by far the noise in the low-resolution dataset, as shown in Table 3.

4.2 Functional model no. 2

We use experimental set-up no. 2 of Table 1. The kernel P, which according to Eq. (12) is used in the functional model of the low-resolution dataset, is chosen according to Eqs. (14) and (15). The cosine taper parameters are set equal to \(p_1 = 150\) and \(p_2 = 230\). Hence, the filtered low-resolution dataset \(P * d_1\) of Eq. (12) is band-limited to degree \(L_1=230\).

The choice of \(p_1\) and \(p_2\) is a trade-off between loss of information in the low-resolution dataset by filtering (i.e. nonzero \(d_1 - P*d_1\)), and a reduction in the area under the side lobes of the cosine taper, which cause oscillations of the filtered Poisson wavelets extending beyond the data area. Moreover, the difference \(p_2 - p_1\) determines how fast the oscillations roll off. The difference \(p_2-p_1=80\) has been fixed after some numerical experiments. Note that the maximum degree of the reference GGM (which is \(L_{\tiny \text{ ref }} = 150\) in our experiments) and the maximum degree of the noisy GGM (which is \(L_{\tiny \text{ GGM }} = 280\) for GOCO05s) impose lower and upper bounds, respectively, on the choice of \(p_1\) and \(p_2\), i.e. \(p_1 \ge 150\) and \(p_2 \le 280\).

The maximum possible value of \(p_2\) is equal to the maximum degree of the GGM, \(L_{\tiny \text{ GGM }}\). The GGM used in this study is GOCO05s. However, for GOCO05s the cumulative height anomaly commission error increases exponentially with increasing degree. It is 1.5 cm at degree 200, but already 3.6 cm at degree 230, and 6.8 cm at degree 250. The height anomaly signal and noise degree variances intersect at degree 257. Hence, when assuming that the noise standard deviation in the high-resolution dataset does not exceed 1–2 mGal (which applies to good terrestrial gravity anomaly datasets), it does not make sense to use a low-resolution dataset complete to the maximum possible degree of \(L_{\tiny \text{ GGM }} = 280\). Another reason in favour of a choice \(L_1 < L_{\tiny \text{ GGM }}\) is the fact that the condition number of the noise covariance matrix of the low-resolution dataset, which is propagated from the full noise covariance matrix of the spherical harmonic coefficients of the GGM, increases with increasing \(L_1\). This makes the computation of the least-squares estimator numerically challenging.

Table 4 shows the statistics of the least-squares residuals for the estimated quasi-geoid model. The SD is 1.94 mGal for the high-resolution dataset. This is close to the SD of the superimposed zero-mean white Gaussian noise of 2.0 mGal. From this we conclude that the model fit is within noise. The situation is different for the low-resolution dataset. The SD of the residuals is 3.42 cm. This is a factor of 2 larger than the average SD of the data noise. Obviously, for some reason, the estimated quasi-geoid model does not fit the low-resolution dataset as one may expect.

Table 4 Statistics of the least-squares residuals using functional model no. 2 of Sect. 2.2
Full size table

Table 5 shows the statistics of the errors in the estimated quasi-geoid model. They are computed over the area of interest.

Table 5 Error statistics (in units of cm) of the quasi-geoid model which has been estimated using the functional model no. 2 of Sect. 2.2 with cosine taper parameters \(p_1 = 150\) and \(p_2 = 230\)
Full size table

The error SD is 3.01 cm. The error SD of the cosine-tapered quasi-geoid model is 1.89 and 1.76 cm, respectively, depending on what control dataset is used. We may compare this with a quasi-geoid model which is estimated using only the high-resolution dataset. The corresponding error SDs are 3.01, 1.58, and 1.71 cm, respectively. Hence, adding the low-resolution dataset does not improve the accuracy of the estimated quasi-geoid model at low frequencies (i.e. below degree 230). This is unexpected, because the low-resolution dataset has a high quality and should improve the estimated quasi-geoid model at the low frequencies. This, and the large least-squares residuals of the dataset \(P*d_1\), which by far exceed the noise, implies that for some reason, the information content in the low-resolution dataset is not fully exploited in the combined least-squares adjustment.

To help understand this result, we run two additional experiments. First of all, we compute the error of the functional model of the (noise-free) low-resolution dataset, Eq. (12), i.e. \((P*d_1)(\cdot ) - \sum _{i=1}^I c_i\, \left( F_1 (P * \varPhi )\right) (\cdot ,z_i)\). We found that it does not exceed 0.01 cm over the area of interest. In a second experiment, we compute a low-resolution quasi-geoid model using the noisy low-resolution dataset and the functional model of Eq. (12). The SD of the residuals is 0.13 cm. This is significantly smaller than for the solution which uses both datasets (SD = 3.42 cm, cf. 1st row in Table 4). Moreover, the error SD of the low-resolution quasi-geoid model is 1.58 cm when evaluated over the area of interest. This is also smaller than the error we obtain when using both datasets (SD = 3.89 cm, cf. 1st row in Table 5).

Our interpretation of the results of these experiments is that a single-scale model is not able to fit two datasets of significantly different bandwidths. Consequently, the weighted least-squares principle forces the solution to match the high-resolution dataset (because it comprises many more observations than the low-resolution dataset) at the price of a larger mismatch to the low-resolution dataset.

To support this interpretation, we choose experimental set-up no. 3 of Table 1, which is similar to experimental set-up no. 2, but involves a high-resolution dataset and a low-resolution dataset with a much larger bandwidth difference of 335% compared to 117% of experimental set-up no. 2. The SD of the least-squares residuals of the low-resolution dataset increases from 3.42 cm (cf. Table 4, 2nd row) to 5.13 cm, whereas the SD of the least-squares residuals of the high-resolution dataset does not change. Hence, when increasing the bandwidth difference between the high-resolution and the low-resolution datasets, the fit of the model to the low-resolution dataset becomes worse. This provides evidence that our interpretation is correct.

4.3 Functional model no. 3

We use experimental set-up no. 4 of Table 1. Note that this set-up uses a high-resolution dataset which extends over a larger area than the experimental set-ups no. 1–3. The reason is the following. When using the functional model of Eq. (22) to estimate a low-resolution quasi-geoid model, the dataset \(d_3\) must be available over the data area, which in all experiments extends by \(5^\circ \) in all directions beyond the area of interest. If we would use the same data area for dataset \(d_2\) when estimating the coefficients \(\{c_{21}\}\) using the functional model of Eq. (20), the dataset \(d_3\) of Eq. (21) would suffer from edge effects. Therefore, the high-resolution dataset \(d_2\) must be available over an area, which is larger than the data area of the dataset \(d_3\). The additional extension must be chosen to reduce the edge effects in dataset \(d_3\) below the noise level. In the experimental set-up no. 4, we use an additional extension by \(5^\circ \) in all directions. Test computations reveal that this choice causes edge effects in dataset \(d_3\), which are negligible compared to the noise. We expect that the additional extension can be chosen much smaller. To find the minimum extension may be the subject of another study.

Table 6 Statistics of the least-squares residuals of the datasets used to estimate the two-scale SRBF model using the functional models of Eqs. (20), (22)
Full size table

Table 6 shows the statistics of the least-squares residuals for the model of Eqs. (20) and (22), respectively. The fit of the high-resolution dataset \(d_2\) to the model of Eq. (20) has a SD of 1.74 mGal. This is close to the superimposed noise of SD = 2 mGal; a similar fit has also been observed when using the functional model no. 2 (cf. Table 4). However, compared to the functional model no. 2, the fit of the dataset \(P*d_1\) to the model has improved dramatically: from 3.42 cm (1st row of Table 4) to 1.47 cm (2nd row of Table 6). A value of 1.47 cm is consistent with the noise in the dataset \(P*d_1\). The fit of the dataset \(d_3\) to the model is 2.69 cm, i.e. dataset \(P*d_1\) has a larger contribution to the model compared to dataset \(d_3\). (Both datasets are evenly large.) This is also consistent with the expectations based on an analysis of the noise covariance matrices of the two datasets (not shown here).

The two-scale model appears to have a much higher quality than the single-scale model of Sect. 4.2. This follows from the statistics of the differences at the control datasets, which are shown in Table 7. For instance, the fit of the two-scale model to the control dataset \(F_1(\delta _{500}*T_2)\) improves from SD = 3.01 cm (2nd row of Table 5) to SD = 1.97 cm (2nd row of Table 7). The fit to the low-resolution control data improves dramatically, too: from 1.89 cm (\(F_1(P*T_1)\), 1st row of Table 5) and 1.76 cm (\(F_1(P*T_2)\), 3rd row of Table 5) to 0.86 and 0.77 cm, respectively. From this we conclude that the two-scale model in combination with the functional model of Eqs. (20), (22) performs better at all wavelengths than any of the two single-scale models. The improvement is a factor of 2.2 for the wavelengths common to the high- and the low-resolution dataset, and a factor of 1.5 for the wavelength not resolved by the low-resolution dataset. The former is due to the fact that the suggested approach which uses the two-scale model fully exploits the higher accuracy of the low-resolution dataset, which is not the case if any of the single-scale models is used.

Table 7 Error statistics (in units of centimetres) of the quasi-geoid model which has been estimated using the functional model no. 3 of Sect. 4.3
Full size table

5 Summary and conclusions

In this study, we investigated different approaches to estimate a local SRBF model of the disturbing potential using weighted least squares from a high-resolution dataset and a low-resolution dataset. In practice, the low-resolution dataset represents a satellite-only spherical harmonic model of the global gravity field equipped with a full noise covariance matrix. Considering the latter as one of the noisy datasets in local quasi-geoid modelling is considered as a significant improvement to the traditional remove–compute–restore approach. It improves the quality of the estimated quasi-geoid model and paves the way to a complete quality description of the estimated quasi-geoid model in terms of a full noise covariance matrix.

Two approaches investigated in this study use a single-scale SRBF model, but differ in the functional model for the low-resolution dataset. The third one uses a two-scale SRBF wavelet model and estimates the coefficients per scale independently of each other.

We showed that the functional model of the low-resolution dataset has to be chosen with care. A hard truncation of the SRBFs at the maximum degree of the low-resolution dataset is the right choice in global quasi-geoid modelling, but provides a wrong functional model in local quasi-geoid modelling. This is in line with the results in (Slobbe et al. 2012). Applying a taper to both the low-resolution dataset and the SRBF model solves this problem.

We also showed that a single-scale SRBF model cannot deal with datasets of different bandwidths. The estimated quasi-geoid model is biased towards the high-resolution dataset at the cost of a poor fit to the low-resolution dataset. The latter appeared to be much worse than the noise in this dataset suggested, which indicates that the information content of the low-resolution dataset is not fully exploited.

We suggested the use of a two-scale SRBF model in combination with a sequential estimation of the scale-dependent coefficients. The latter differs from what has been suggested in the literature in the context of a multi-scale analysis. In this way, we ensure that the two datasets are weighted in line with their accuracy, the information content in the low-resolution and high-resolution datasets is fully exploited, and the misfit of the estimated quasi-geoid model is consistent with the noise in the datasets.

A challenge of the suggested approach in applications involving real datasets is the additional extension of the data area for the high-resolution dataset. In this study, a safe choice has been made to make edge effects insignificant. In applications involving real datasets, access to high-quality terrestrial gravity anomaly datasets of neighbouring countries is not guaranteed. How much the data area needs to be extended and whether data with reduced accuracy can be used in the additional area without introducing distortions in the estimated quasi-geoid model has to be investigated.

It would be interesting to compare the two-scale approach suggested in this study with a multi-scale approach, which estimates the coefficients at the two scales simultaneously as suggested in Lieb (2017). Some preliminary experiments (not shown here) indicate that such a multi-scale approach provides a sub-optimal low-resolution quasi-geoid model compared to a sequential estimation as suggested here. Whether this may be corrected for by a further optimization of the multi-scale approach, for example, by introducing constraints between the model coefficients associated with different scales may be the subject of a future study.