Evaluation of gravitational curvatures of a tesseroid in spherical integral kernels

Abstract

Proper understanding of how the Earth’s mass distributions and redistributions influence the Earth’s gravity field-related functionals is crucial for numerous applications in geodesy, geophysics and related geosciences. Calculations of the gravitational curvatures (GC) have been proposed in geodesy in recent years. In view of future satellite missions, the sixth-order developments of the gradients are becoming requisite. In this paper, a set of 3D integral GC formulas of a tesseroid mass body have been provided by spherical integral kernels in the spatial domain. Based on the Taylor series expansion approach, the numerical expressions of the 3D GC formulas are provided up to sixth order. Moreover, numerical experiments demonstrate the correctness of the 3D Taylor series approach for the GC formulas with order as high as sixth order. Analogous to other gravitational effects (e.g., gravitational potential, gravity vector, gravity gradient tensor), numerically it is found that there exist the very-near-area problem and polar singularity problem in the GC east–east–radial, north–north–radial and radial–radial–radial components in spatial domain, and compared to the other gravitational effects, the relative approximation errors of the GC components are larger due to not only the influence of the geocentric distance but also the influence of the latitude. This study shows that the magnitude of each term for the nonzero GC functionals by a grid resolution 15$^{{\prime } }\,\times$ 15$^{{\prime }}$ at GOCE satellite height can reach of about 10$^{-16}$ m$^{-1}$ s$^{2}$ for zero order, 10$^{-24 }$ or 10$^{-23}$ m$^{-1}$ s$^{2}$ for second order, 10$^{-29}$ m$^{-1}$ s$^{2}$ for fourth order and 10$^{-35}$ or 10$^{-34}$ m$^{-1}$ s$^{2}$ for sixth order, respectively.

Appendices

Appendix A: Derivation of the 3D GC formulas in spherical integral kernels

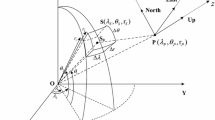
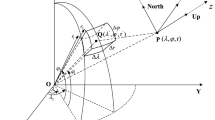
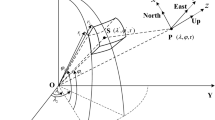
The integral expressions of the GC functionals (e.g., the third-order derivatives of GP) given by a tesseroid mass body can be expressed in spherical coordinates in the local East–North–Up (ENU) topocentric reference system of the computation point $P(\lambda _P ,\theta _P ,r_P )$. The expressions of the 10 GC functionals can be referred in Tóth (2005), Tóth and Földváry (2005), Casotto and Fantino (2009), Šprlák et al. (2016), Šprlák and Novák (2015, 2016, 2017).

After substituting the expressions of Table 4 into the expressions of the 10 GC functionals and mathematical simplification, the 3D integral expressions of GC functionals of a tesseroid in spherical coordinates in the local East–North–Up (ENU) topocentric reference system can be obtained as

Table 5 Detailed expressions of $F_m$ and $X\left( {\lambda _0 ,\theta _0 ,r_0 } \right)$ in Eqs. (B1)–(B5) with $k_0 =G\rho _S r_0^2 \cos \theta _0$,$l_{P0} =\sqrt{r_P^2 +r_0^2 -2r_P r_0 \cos \psi _0 }$,$\cos \psi _0 =\sin \theta _P \sin \theta _0 +\cos \theta _P \cos \theta _0 \cos \left( {\lambda _P -\lambda _0 } \right)$, $A_0 =\cos \theta _P \sin \theta _0 -\sin \theta _p \cos \theta _0 \cos \left( {\lambda _P -\lambda _0 } \right)$ and $B_0 =r_P -r_0 \cos \psi _0$

$$\begin{aligned} V_{xxx}^{T3D}= & {} \mathop \int \limits _{\lambda _1 }^{\lambda _2 } \mathop \int \limits _{\theta _1 }^{\theta _2 } \mathop \int \limits _{r_1 }^{r_2 } \left( -\frac{15kr_S ^{3}\cos ^{3}\theta _S \sin ^{3}\left( {\lambda _P -\lambda _S } \right) }{l_{PS}^7 } \right. \nonumber \\&+\,\frac{9kr_S \cos \theta _S \sin \left( {\lambda _P -\lambda _S } \right) }{r_P \sin \theta _P \cos \theta _P l_{PS}^5 }\left( r_S \cos ^{2}\theta _P A \right. \nonumber \\&\left. +\,\sin \theta _P \cos \theta _P B+r_S \sin \theta _P \cos \theta _S \cos \left( {\lambda _P -\lambda _S } \right) \right) \nonumber \\&\left. +\frac{3kr_S \cos \theta _S \sin \left( {\lambda _P -\lambda _S } \right) }{r_P^2 \cos ^{2}\theta _P l_{PS}^3 }\left( {1-2\cos ^{2}\theta _P } \right) \right) \hbox {d}r_S \hbox {d}\theta _S \hbox {d}\lambda _S \end{aligned}$$

(A1)

$$\begin{aligned} V_{xxy}^{T3D}= & {} \mathop \int \limits _{\lambda _1 }^{\lambda _2 } \mathop \int \limits _{\theta _1 }^{\theta _2 } \mathop \int \limits _{r_1 }^{r_2 } \left( \frac{15kr_S ^{3}\cos ^{2}\theta _S \sin ^{2}\left( {\lambda _P -\lambda _S } \right) A}{l_{PS}^7 } \right. \nonumber \\&-\,\frac{3kr_S A\left( {\cos \theta _P B+r_S \cos \theta _S \cos \left( {\lambda _P -\lambda _S } \right) +r_S \sin \theta _P A} \right) }{r_P \cos \theta _P l_{PS}^5 }\nonumber \\&-\,\frac{1}{r_P^2 \cos ^{2}\theta _P l_{PS}^3 }kr_S \sin \theta _P \left( \cos \theta _S \cos \left( {\lambda _P -\lambda _S } \right) \nonumber \right. \\&\left. \left. -\cos \theta _P \cos \psi +\sin \theta _P A \right) \right) \hbox {d}r_S \hbox {d}\theta _S \hbox {d}\lambda _S \end{aligned}$$

(A2)

$$\begin{aligned} V_{xxz}^{T3D}= & {} \mathop \int \limits _{\lambda _1 }^{\lambda _2 } \mathop \int \limits _{\theta _1 }^{\theta _2 } \mathop \int \limits _{r_1 }^{r_2 } \left( -\frac{15kr_S^2 \cos ^{2}\theta _S \sin ^{2}\left( {\lambda _P -\lambda _S } \right) B}{l_{PS}^7 } \right. \nonumber \\&+\frac{3k}{r_P^2 \cos \theta _P l_{PS}^5 }(2r_S ^{2}\cos \theta _P \cos ^{2}\theta _S \sin ^{2}\left( {\lambda _P -\lambda _S } \right) \left( {r_P -1} \right) \nonumber \\&+r_P B\left( {r_S \cos \theta _S \cos \left( {\lambda _P -\lambda _S } \right) +r_S \sin \theta _P A+r_P \cos \theta _P B} \right) )\nonumber \\&\left. +\frac{kr_S ( {\cos \theta _S \cos ( {\lambda _P {-}\lambda _S } ){+}\sin \theta _P A} ){+}k\cos \theta _P ( {B-r_P } )}{r_P^2 \cos \theta _P l_{PS}^3 }\right) \hbox {d}r_S \hbox {d}\theta _S \hbox {d}\lambda _S \end{aligned}$$

(A3)

$$\begin{aligned} V_{xyz}^{T3D}= & {} \mathop \int \limits _{\lambda _1 }^{\lambda _2 } \mathop \int \limits _{\theta _1 }^{\theta _2 } \mathop \int \limits _{r_1 }^{r_2 } \frac{15kr_S^2 \cos \theta _S \sin \left( {\lambda _P -\lambda _S } \right) AB}{l_{PS}^7 }\hbox {d}r_S \hbox {d}\theta _S \hbox {d}\lambda _S , \end{aligned}$$

(A4)

$$\begin{aligned} V_{yyx}^{T3D}= & {} \mathop \int \limits _{\lambda _1 }^{\lambda _2 } \mathop \int \limits _{\theta _1 }^{\theta _2 } \mathop \int \limits _{r_1 }^{r_2 } \left( -\frac{15kr_S ^{3}\cos \theta _S \sin \left( {\lambda _P -\lambda _S } \right) A^{2}}{l_{PS}^7 }+ \right. \nonumber \\&\frac{3kr_S \cos \theta _S \sin \left( {\lambda _P -\lambda _S } \right) }{r_P^2 \cos \theta _P l_{PS}^5 }\left( 2r_S \sin \theta _p \left( {r_P -1} \right) A \right. \nonumber \\&\left. \left. + r_P \cos \theta _P \left( {B+r_S \cos \psi } \right) \right) \right) \hbox {d}r_S \hbox {d}\theta _S \hbox {d}\lambda _S \end{aligned}$$

(A5)

$$\begin{aligned} V_{yyy}^{T3D}= & {} \mathop \int \limits _{\lambda _1 }^{\lambda _2 } \mathop \int \limits _{\theta _1 }^{\theta _2 } \mathop \int \limits _{r_1 }^{r_2 } \frac{3kr_S A}{l_{PS}^5 }\left( {\frac{5r_S^2 A^{2}}{l_{PS}^2 }-3} \right) \hbox {d}r_S \hbox {d}\theta _S \hbox {d}\lambda _S \end{aligned}$$

(A6)

$$\begin{aligned} V_{yyz}^{T3D}= & {} \mathop \int \limits _{\lambda _1 }^{\lambda _2 } \mathop \int \limits _{\theta _1 }^{\theta _2 } \mathop \int \limits _{r_1 }^{r_2 } \frac{3kB}{l_{PS}^5 }\left( {-\frac{5r_S^2 A^{2}}{l_{PS}^2 }+1} \right) \hbox {d}r_S \hbox {d}\theta _S \hbox {d}\lambda _S \end{aligned}$$

(A7)

$$\begin{aligned} V_{zzx}^{T3D}= & {} \mathop \int \limits _{\lambda _1 }^{\lambda _2 } \mathop \int \limits _{\theta _1 }^{\theta _2 } \mathop \int \limits _{r_1 }^{r_2 } \frac{3kr_S \cos \theta _S \sin \left( {\lambda _P -\lambda _S } \right) }{l_{PS}^5 }\left( {-\frac{5B^{2}}{l_{PS}^2 }+1} \right) \hbox {d}r_S \hbox {d}\theta _S \hbox {d}\lambda _S \end{aligned}$$

(A8)

$$\begin{aligned} V_{zzy}^{T3D}= & {} \mathop \int \limits _{\lambda _1 }^{\lambda _2 } \mathop \int \limits _{\theta _1 }^{\theta _2 } \mathop \int \limits _{r_1 }^{r_2 } \frac{3kr_S A}{l_{PS}^5 }\left( {\frac{5B^{2}}{l_{PS}^2 }-1} \right) \hbox {d}r_S \hbox {d}\theta _S \hbox {d}\lambda _S \end{aligned}$$

(A9)

$$\begin{aligned} V_{zzz}^{T3D}= & {} \mathop \int \limits _{\lambda _1 }^{\lambda _2 } \mathop \int \limits _{\theta _1 }^{\theta _2 } \mathop \int \limits _{r_1 }^{r_2 } \frac{3kB}{l_{PS}^5 }\left( {3-\frac{5B^{2}}{l_{PS}^2 }} \right) \hbox {d}r_S \hbox {d}\theta _S \hbox {d}\lambda _S \end{aligned}$$

(A10)

As we adopt the same expressions of the 10 GC functionals as in Tóth (2005), Casotto and Fantino (2009), the representations of Eqs. (A1)–(A10) are equivalent to the Newton integrals as shown in Šprlák and Novák (2015). One could use the following Laplace identity equations to confirm the validity of the GC expressions (Casotto and Fantino 2009; Šprlák and Novák 2016; Šprlák et al. 2016):

$$\begin{aligned} V_{xxx}^{T3D} +V_{yyx}^{T3D} +V_{zzx}^{T3D}= & {} 0, \end{aligned}$$

(A11)

$$\begin{aligned} V_{xxy}^{T3D} +V_{yyy}^{T3D} +V_{zzy}^{T3D}= & {} 0, \end{aligned}$$

(A12)

$$\begin{aligned} V_{xxz}^{T3D} +V_{yyz}^{T3D} +V_{zzz}^{T3D}= & {} 0. \end{aligned}$$

(A13)

Appendix B: 3D Taylor series approach for the GC functionals

In practical calculations, one could use these iterative relationships to simplify the calculation process; therefore, the 3D zero-order, second-order, fourth-order and sixth-order tesseroid expressions of the GC functionals can be given as:

$$\begin{aligned} F_0= & {} \Delta ^{0}, \end{aligned}$$

(B1)

$$\begin{aligned} F_2= & {} \Delta ^{0}+\Delta ^{2}=F_0 +\Delta ^{2}, \end{aligned}$$

(B2)

$$\begin{aligned} F_4= & {} \Delta ^{0}+\Delta ^{2}+\Delta ^{4}=F_2 +\Delta ^{4}, \end{aligned}$$

(B3)

$$\begin{aligned} F_6= & {} \Delta ^{0}+\Delta ^{2}+\Delta ^{4}+\Delta ^{6}=F_4 +\Delta ^{6}, \end{aligned}$$

(B4)

$$\begin{aligned} \Delta ^{6}= & {} \frac{1}{13824}\Delta \lambda \Delta \theta \Delta r\left( {X_{222} \Delta \lambda ^{2}\Delta \theta ^{2}\Delta r^{2}} \right) \nonumber \\&+\,\frac{1}{46080}\Delta \lambda \Delta \theta \Delta r(X_{420} \Delta \lambda ^{4}\Delta \theta ^{2}+X_{402} \Delta \lambda ^{4}\Delta r^{2}\nonumber \\&+\,X_{240} \Delta \lambda ^{2}\Delta \theta ^{4}\nonumber \\&+\,X_{204} \Delta \lambda ^{2}\Delta r^{4}+X_{042} \Delta \theta ^{4}\Delta r^{2}+X_{024} \Delta \theta ^{2}\Delta r^{4}) \nonumber \\&+\,\frac{1}{322560}\Delta \lambda \Delta \theta \Delta r\left( X_{600} \Delta \lambda ^{6}+X_{060} \Delta \theta ^{6}\right. \nonumber \\&\left. +\,X_{006} \Delta r^{6} \right) . \end{aligned}$$

(B5)

Herein, the $\Delta ^{6}$ term is provided, and the other lower terms (e.g., $\Delta ^{0}$, $\Delta ^{2}$and $\Delta ^{4})$ can be referred in Eqs. (13)–(15) of Shen and Deng (2016).

Herein, the Mathematica code file (Code.nb) for the detailed expressions of the 3D zero-order, second-order, fourth-order and sixth-order tesseroid formulas of the GC functionals is provided on a request addressing to W.B. Shen. The code file contains two parts: a) the expressions of the spherical integral kernels for the 10 different GC functionals; b) the processes of different order (zero-order, second-order, fourth-order and sixth-order) Taylor series expansion approach for the 10 different GC functionals. Taking the GC component $V_{xxx}^{T3D}$ for example, the first part in the code file presents the expression of spherical integral kernels for $V_{xxx}^{T3D}$ as $Vxxx[G\_,\rho \_,\lambda p\_,\theta p\_,rp\_,\lambda 0\_,\theta 0\_,r0\_]$, which is the function definition in Mathematica; $\lambda p,\theta p,rp$ and $\lambda 0,\theta 0,r0$ are the spherical coordinates of the computation point P and the integration point $S_0$ with the symbol definition in the Mathematica code file. Then in the second part of the code file, it gives the different coefficient parameters expressions with different order (zero order with Vxxx000; second-order with Vxxx200,Vxxx020,Vxxx002; fourth order with Vxxx220, Vxxx022, ..., Vxxx004; and sixth order with Vxxx222, ..., Vxxx420, ..., Vxxx006) from Eq. (3). After substituting the coefficient parameters into Eqs. (B1)–(B5), it provides the final expressions for 3D zero-order (GCVxxx0), second-order (GCVxxx2), fourth-order (GCVxxx4) and sixth-order (GCVxxx6) tesseroid formulas for the GC component $V_{xxx}^{T3D}$.