Skip to main content
SpringerLink
Log in

Methods of harmonic synthesis for global geopotential models and their first-, second- and third-order gradients

  • Original Article
  • Published:
Journal of Geodesy Aims and scope Submit manuscript

An Erratum to this article was published on 05 October 2015

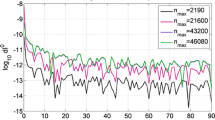
Abstract

Four widely used algorithms for the computation of the Earth’s gravitational potential and its first-, second- and third-order gradients are examined: the traditional increasing degree recursion in associated Legendre functions and its variant based on the Clenshaw summation, plus the methods of Pines and Cunningham–Metris, which are free from the singularities that distinguish the first two methods at the geographic poles. All four methods are reorganized with the lumped coefficients approach, which in the cases of Pines and Cunningham–Metris requires a complete revision of the algorithms. The characteristics of the four methods are studied and described, and numerical tests are performed to assess and compare their precision, accuracy, and efficiency. In general the performance levels of all four codes exhibit large improvements over previously published versions. From the point of view of numerical precision, away from the geographic poles Clenshaw and Legendre offer an overall better quality. Furthermore, Pines and Cunningham–Metris are affected by an intrinsic loss of precision at the equator and suffer from additional deterioration when the gravity gradients components are rotated into the East-North-Up topocentric reference system.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Abramowitz M, Stegun IA (1964) Handbook of mathematical functions with formulas, graphs, and mathematical tables. Dover Publications, New York

    Google Scholar 

  • Albertella A, Migliaccio F, Sansò F, Tscherning CC (2000) The space-wise approach—overall scientific data strategy. In: Sünkel H (ed) From Eötvös to mGal, Final Report, ESA/ESTEC contract No. 13392/98/NL/GD, GOCE Study Report. http://esamultimedia.esa.int/docs/Eoetvoes2Mgal_FinalReport_13392_98.pdf

  • Albertella A, Migliaccio F, Sansò F (2002) GOCE: the earth gravity field by space gradiometry. Celestial Mech Dyn Astron 83:1–15

    Google Scholar 

  • Arsov K, Pail R (2003) Assessment of two methods for gravity field recovery from GOCE GPS-SST orbit solutions. Adv Geosci 1: 121–126

    Article  Google Scholar 

  • Balmino G, Barriot J-P, Valès N (1990) Non-singular formulation of the gravity vector and gravity gradient tensor in spherical harmonics. Manuscr Geod 15(1): 11–16

    Google Scholar 

  • Balmino G, Barriot J-P, Koop R, Middel B, Thong NC, Vermeer M (1991) Simulation of gravity gradients: a comparison study. Bull Géod 65(4): 218–229

    Article  Google Scholar 

  • Bettadpur SV, Schutz BE, Lundberg JB (1992) Spherical harmonic synthesis and least squares computations in satellite gravity gradiometry. Bull Géod 66(3): 261–271

    Article  Google Scholar 

  • Casotto S, Fantino E (2007) Evaluation of methods for spherical harmonic synthesis of the gravitational potential and its gradients. Adv Sp Res 40: 69–75

    Article  Google Scholar 

  • Casotto S, Fantino E (2008) Gravitational gradients by tensor analysis with application to spherical coordinates. J Geod. doi:10.1007/s00190-008-0276-z

  • Clenshaw CW (1955) A note on the summation of Chebyshev series. Math Tab Automat Comput 9: 118–120

    Google Scholar 

  • Cunningham LE (1970) On the computation of the spherical harmonic terms needed during the numerical integration of the orbital motion of an artificial satellite. Celestial Mech 2: 207–216

    Article  Google Scholar 

  • Deprit A (1979) Note on the summation of Legendre Series. Celestial Mech 2: 319–323

    Article  Google Scholar 

  • Drinkwater MR, Floberghagen R, Haagmans R, Muzi D, Popescu A (2003) GOCE: ESA’s first earth explorer core mission. In: Beutler GB, Drinkwater M, Rummel R, von Steiger R (eds) Earth gravity field from space—from sensors to earth sciences. Space Sciences Series of ISSI, vol 18. Kluwer, Dordrecht, pp 419–432

  • Eddy WF, McCarthy JJ, Pavlis DE, Marshall JA, Luthcke SB, Tsaussi LS, Leung G, Williams DA (1990) GEODYN II—systems description, vol 1. STX Systems Corp., prepared for NASA/GSFC Space Geodesy Branch, Greenbelt

  • Ellis TMR, Philips IR, Lahey TM (1994) FORTRAN 90 programming. Addison-Wesley, England

    Google Scholar 

  • ESA (1999) Gravity field and steady-state ocean circulation mission, ESA SP-1233(1). Report for mission selection of the four candidate earth explorer missions. http://www.esa.int/esaLP/GTCVCKSC_LPgoce_0.html

  • Garmier R, Barriot J-P (2001) Ellipsoidal harmonic expansions of the gravitational potential: theory and application. Celestial Mech Dyn Astron 79: 235–275

    Article  Google Scholar 

  • Gautschi W (1967) Computational aspects of three-term recurrence relations. SIAM Rev 9(1): 24–82

    Article  Google Scholar 

  • Gill E, Montenbruck O, Terzibaschian Th (2000) An Autonomous Navigation System for the German Small satellite Mission BIRD. Paper AAS 00-122

  • Gottlieb RG (1993) Fast gravity, gravity partials, normalized gravity, gravity gradient torque and magnetic field: derivation, code and data, NASA Contractor Report No. 188243

  • Heiskanen WA, Moritz H (1967) Physical geodesy. Freeman, San Francisco

    Google Scholar 

  • Hobson EW (1965) The theory of spherical and ellipsoidal harmonics. Chelsea Publishing Company, New York

    Google Scholar 

  • Holmes SA, Featherstone WE (2002a) A unified approach to the Clenshaw summation and the recursive computation of very high degree and order normalized associated Legendre functions. J Geod 76: 279–299

    Article  Google Scholar 

  • Holmes SA, Featherstone WE (2002b) SHORT NOTE: extending simplified high-degree synthesis methods to second latitudinal derivatives of geopotential. J Geod 76: 447–450

    Article  Google Scholar 

  • Ilk KH (1983) Ein Beitrag zur Dynamik ausgedehnter Körper—Gravitationswechselwirkung. PhD Thesis, Bayerischen Akademie der Wissenschaften, Munchen

  • Jackson MJ, Pollack HN, Sutton ST (1991) On the distribution of anomalous mass within the earth: forward models of the gravitational potential spectrum using ensembles of discrete mass elements. Geophys J Int 107: 83–94

    Article  Google Scholar 

  • Jekeli C, Lee JK, Kwon HJ (2007) On the computation and approximation of ultra-high degree spherical harmonics. J Geod 81: 603–615

    Article  Google Scholar 

  • Junkins JL (1976) An Investigation of Finite Element Representations of the Geopotential. AIAA J 14(6): 803–808

    Article  Google Scholar 

  • Junkins JL, Engels RS (1979) The finite element approach in gravity modeling. Manuscr Geod 4: 185–206

    Google Scholar 

  • Keller W, Sharifi MA (2005) Satellite gradiometry using a satellite pair. J Geod 78: 544–557

    Article  Google Scholar 

  • Konopliv AS, Binder AB, Hood LL, Kucinskas AB, Sjogren WL, Williams JG (1998) Improved gravity field of the moon from Lunar prospector. Science 281: 1476–1480

    Article  Google Scholar 

  • Koop R, Stelpstra D (1989) On the computation of the gravitational potential and its first and second order derivatives. Manuscr Geod 14: 373–382

    Google Scholar 

  • Koop R (1993) Global gravity field modeling using satellite gravity gradiometry, The Netherlands Geodetic Comission, Publications on Geodesy, New Series, No. 38, Delft, The Netherlands

  • Koop R, Visser P, van den Ijssel J, Klees R (2000) Detailed scientific Data Processing Approach. In: Sünkel H (ed) From Eötvös to mGal, Final Report, ESA/ESTEC contract No. 13392/98/NL/GD, GOCE Study Report. Online version at http://esamultimedia.esa.int/docs/Eoetvoes2Mgal_FinalReport_13392_98.pdf

  • Lemoine FG, Kenyon SC, Factor JK, Trimmer RG, Pavlis NK, Chinn DS, Cox CM, Klosko SM, Luthcke SB, Torrence MH, Wang YM, Williamson RG, Pavlis EC, Rapp RH, Olson TR (1998) The Development of the Joint NASA GSFC and NIMA Geopotential Model EGM96. NASA/TP-1998-206861, NASA Goddard Space Flight Center

  • Long AC, Cappellari JO, Velez CE, Fuchs AJ (eds) (1989) Goddard trajectory determination system (GTDR), Mathematical Theory (Revision 1). NASA/GSFC Report FDD/552-89/0001, Greenbelt

  • Lundberg JB, Schutz BE (1988) Recursion formulas for Legendre functions for use with nonsingular geopotential models. J Guidance Control Dyn 11(1): 31–38

    Article  Google Scholar 

  • McCarthy DD, Petit G (2004) IERS conventions (2003) (IERS Technical Note No. 32). BKG, Frankfurt am Main. Online version at http://www.iers.org/iers/publications/tn/tn32/

  • Metris G, Xu J, Wytrzyszczak I (1999) Derivatives of the gravity potential with respect to rectangular coordinates. Celestial Mech Dyn Astron 71:137–151. http://wwwrc.obs-azur.fr/cerga/mecanique/potential/

  • Michelson I (1970) Simplified analysis of mascon modification of Apollo-type orbits. Pure Appl Geophys 79: 5–13

    Article  Google Scholar 

  • Migliaccio F, Reguzzoni M, Sansò F, Tscherning CC (2004) An Enhanced Space-Wise Simulation for GOCE Data Reduction. In: Proceedings of the second international GOCE user workshop (ESA SP-569)

  • Migliaccio F, Reguzzoni M, Sansò F, Tselfes N, Tscherning CC, Veicherts M (2006) The latest test of the space-wise approach for GOCE data analysis. In: Proceedings of the third international GOCE user workshop (ESA SP-627)

  • Montenbruck O, Gill E (2000) Satellite orbits—models, methods, and applications. Springer, Berlin

    Google Scholar 

  • Pail R, Schuh WD, Wermuth M (2005) GOCE gravity field processing. In: Jekeli C, Bastos L, Fernandes J (eds) Gravity, Geoid and Space Missions International Association of Geodesy Symposia, vol 129. Springer, Berlin, pp 36–41

  • Pail R, Metzler B, Preimesberger T, Lackner B, Wermuth M (2006) GOCE quick-look gravity field analysis in the framework of HPF, in Proceedings of the Third International GOCE User Workshop (ESA SP-627)

  • Pavlis NK, Holmes SA, Kenyon SC, Schmidt D, Trimmer R (2005) A Preliminary Gravitational Model to Degree 2160. In: Jekeli C, Bastos L, Fernandes J (eds) “Gravity, Geoid and Space Missions” International Association of Geodesy Symposia, vol 129. Springer, Berlin, pp 18–23

  • Pines S (1973) Uniform representation of the gravitational potential and its derivatives. AIAA J 11: 1508–1511

    Article  Google Scholar 

  • Press WH, Teukolsky SA, Vetterling WT, Flannery BP (1992) Numerical Recipes in Fortran 77. Cambridge University Press, Cambridge

    Google Scholar 

  • Robin L (1957) Fonctions Sphériques de Legendre et Fonctions Sphéroidales—Tome I. Gauthier, Villars, Paris

  • Reguzzoni M (2003) From the time-wise to space-wise GOCE observables. Adv Geosci 1: 137–142

    Google Scholar 

  • Rummel R, Colombo OL (1985) Gravity field determination from satellite gradiometry. Bull Géod 59(3): 233–246

    Article  Google Scholar 

  • Rummel R, Van Gelderen M, Koop R, Schrama E, Sansò F, Brovelli M, Migliaccio F, Sacerdote F (1993) Spherical harmonic analysis of satellite gradiometry. Publications on Geodesy, New Series, No. 39, Netherlands Geodetic Commission

  • Sansone G (1991) Orthogonal functions. Dover Publications, New York

    Google Scholar 

  • Smoktunowicz A (2002) Backward stability of Clenshaw’s algorithm. BIT Numer Math 42: 600–610

    Article  Google Scholar 

  • Sneeuw N (2000) A semi-analytical approach to gravity field analysis from satellite observations. Deutsche Geodätische Kommission, Reihe C, Heft Nr. 527, München

  • Spencer JL (1976) Pines’ nonsingular gravitational potential derivation, description and implementation. Technical report, NASA Contract No. 9-13970

  • Sutton ST, Pollack HN, Jackson MJ (1991) Spherical harmonic representation of the gravitational potential of spherical mass elements. Geophys J Int 107: 77–82

    Article  Google Scholar 

  • Thông NC, Grafarend EW (1989) A spheroidal harmonic model of the terrestrial gravitational field. Manuscr Geod 14: 285–304

    Google Scholar 

  • Tóth Gy (2005) The gradiometric-geodynamic boundary value problem. In: Jekeli C, Bastos L, Fernandes J (eds) “Gravity, Geoid and Space Missions” International Association of Geodesy Symposia. vol 129. Springer, Berlin, pp 352–257

  • Tóth Gy, Földváry L (2005) Effect of geopotential model errors on the projection of GOCE gradiometer observables. In: Jekeli C, Bastos L, Fernandes J (eds) “Gravity, Geoid and Space Missions” International Association of Geodesy Symposia, vol 129. Springer, Berlin, pp 72–76

  • Tscherning CC (1976) Computation of the second-order derivatives of the normal potential based on the representation by a Legendre series. Manuscr Geod 1: 71–92

    Google Scholar 

  • Tscherning CC, Poder K (1982) Some geodetic applications of Clenshaw summation. Boll Geod Sci Aff XLI/4: 349–375

    Google Scholar 

  • Tscherning CC, Rapp RH, Goad C (1983) A comparison of methods for computing gravimetric quantities from high degree spherical harmonic expansions. Manuscr Geod 8: 249–272

    Google Scholar 

  • Vallado DA (2001) Fundamentals of astrodynamics and applications. Microcosm Press/Kluwer, El Segundo/Dordrecht

  • Vanicek P, Krakiwski EJ (1986) Geodesy: the concepts. Elsevier, Amsterdam

    Google Scholar 

  • Winch DE, Roberts PH (1995) Derivativs of addition theorems for Legendre functions. J Austral Math Soc Ser B 37: 212–234

    Article  Google Scholar 

  • Xu G (2003) GPS theory, algorithms and applications. Springer, Heidelberg

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Dipartimento di Astronomia, Università di Padova, Vicolo dell’Osservatorio 3, 35122, Padua, Italy

    E. Fantino & S. Casotto

  2. Center for Space Studies (CISAS) “G. Colombo”, Università di Padova, Via Venezia 15, 35131, Padua, Italy

    S. Casotto

Authors
  1. E. Fantino
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. S. Casotto
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S. Casotto.

Additional information

An erratum to this article is available at http://dx.doi.org/10.1007/s00190-015-0859-4.

Electronic supplementary material

The Below is the Electronic Supplementary Material.

ESM (PDF 201 kb)

ESM (PDF 1730 kb)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Fantino, E., Casotto, S. Methods of harmonic synthesis for global geopotential models and their first-, second- and third-order gradients. J Geod 83, 595–619 (2009). https://doi.org/10.1007/s00190-008-0275-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00190-008-0275-0

Keywords

Search

Navigation