Joint analysis of recurrent event data with additive–multiplicative hazards model for the terminal event time

Abstract

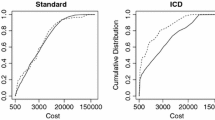
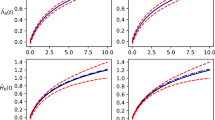
Recurrent event data are often collected in longitudinal follow-up studies. In this article, we propose a semiparametric method to model the recurrent and terminal events jointly. We present an additive–multiplicative hazards model for the terminal event and a proportional intensity model for the recurrent events, and a shared frailty is used to model the dependence between the recurrent and terminal events. We adopt estimating equation approaches for inference, and the asymptotic properties of the resulting estimators are established. The finite sample behavior of the proposed estimators is evaluated through simulation studies. An application to a medical cost study of chronic heart failure patients from the University of Virginia Health System is illustrated.

Appendices

Appendix A: Proofs of asymptotic results

In this section, we will use the same notation defined above and all limits are taken at $n \rightarrow \infty$. Let $\bar{q}(t)$ be the limit of $\bar{Q}(t;\beta _0,\eta _0)$. In order to study the asymptotic distributions of $\hat{\beta }, \hat{\eta }$ and $\hat{\gamma },$ we need the following regularity conditions:

• (C1) $P(Y \ge \tau , v>0)>0,$ $\Lambda _0(\tau )>0$ and $E\{N(\tau )^2\} <\infty .$

• (C2) $G(t)=E\{v I(Y \ge t) \exp (\gamma _{0}'X)\}$ is a continuous function for $t \in [0, \tau ].$

• (C3) A is nonsingular, where

$$\begin{aligned} A=E\left[ \int _0^\tau \left\{ Q_i(\beta _0, \eta _0)-\bar{q}(t)\right\} \Delta _i(t)V_i\left( \begin{array}{c}\dot{h}(\beta _0' Z_i)Z_id{\mathcal A}_0(t)\\ \dot{g}(\eta _0' W_i)W_idt \end{array}\right) '\right] , \end{aligned}$$

Define $R(t)=G(t)\Lambda _0(t)$, $H(t)=\int _0^t G(u)d\Lambda _0(u),$ $D_1=E\{\exp \{ \alpha _0' X_{i}^*\} X_{i}^{* \otimes 2}\},$

$$\begin{aligned} \kappa _i(t)=\sum _{j=1}^{m_i} \left\{ \int _t^{\tau } \frac{I(T_{ij }\le u \le Y_i)d{H}(u)}{{R}^2(u)}-\frac{I(t<T_{ij} \le \tau )}{{R}(T_{ij})} \right\} , \end{aligned}$$

and

$$\begin{aligned} e_i= X_{i}^* \left[ \frac{ m_i}{F(Y_i)}-\exp \{\alpha _0'X_{i}^*\} \right] -\int \frac{x^*m\kappa _i(y) dP_1(x^*,y,m)}{{F}(y)}, \end{aligned}$$

where $P_1(x^*,y,m)$ is the joint probability measure of $(X_{i}^*, Y_i, m_i).$ Let $\phi _{1i}$ denote the vector $D_1^{-1}e_i$ without the first entry and $\phi _{2i}$ denote the first entry of $D_1^{-1}e_i$. Set $\varphi _i(t)=\kappa _i(t)+\phi _{2i}$, and $b_i(y,x)=\varphi _i(y)+\phi _{1i}' x$.

Proof of Theorem 1

Under conditions (C1) and (C2), it follows from Wang et al. (2001) that

$$\begin{aligned} n^{1/2}\{\hat{\Lambda }_0(t)-\Lambda _0(t)\}&=n^{-1/2} \Lambda _0(t)\sum _{i=1}^n\varphi _i(t)+o_p(1), \end{aligned}$$

(A.1)

holds uniformly in t, and

$$\begin{aligned} n^{1/2}\{\hat{\gamma }-\gamma _0\}&=n^{-1/2} \sum _{i=1}^n\phi _{1i}+o_p(1). \end{aligned}$$

(A.2)

By using the Taylor expansion theorem, (A.1) and (A.2), we have

$$\begin{aligned} \hat{V}_{i}-V_{i}=&m_i\left\{ \hat{\Lambda }_0(Y_i)e^{\hat{\gamma }' X_i}\right\} ^{-1}-m_i\left\{ \Lambda _0(Y_i)e^{\gamma _0' X_i}\right\} ^{-1}\nonumber \\ =&-m_i\left\{ \Lambda _0(Y_i)e^{\gamma _0' X_i}\right\} ^{-2}\big [e^{\gamma _0' X_i}\left\{ \hat{\Lambda }_0(Y_i)-\Lambda _0(Y_i)\right\} \nonumber \\&+\Lambda _0(Y_i)e^{\gamma _0' X_i}(\hat{\gamma }-\gamma _0)'X_i\big ]\nonumber \\&+o(||\hat{\gamma }-\gamma _0|| +|\hat{\Lambda }_0(Y_i)-\Lambda _0(Y_i)|)\nonumber \\ =&-m_i\left\{ \Lambda _0(Y_i)e^{\gamma _0' X_i}\right\} ^{-1}n^{-1}\left\{ \sum _{j=1}^n\varphi _j(Y_i)+ \sum _{j=1}^n\phi _{1j}'X_i\right\} +o_p(n^{-1/2}), \end{aligned}$$

(A.3)

where $o_p(.)$ is independent of i since (A.1) holds uniformly in t.

Define

$$\begin{aligned} dM^D_i(t)=dN^D_i(t)-\Delta _i(t) V_i\{\alpha _0(t)h(\beta _0'Z_i)+g(\eta _0' W_i)\}dt. \end{aligned}$$

Then $M^D_i(t)$ is a zero-mean process. Hence using the functional version of the law of large numbers and Lemma A.1 of Lin and Ying (2001), we get

$$\begin{aligned}&n^{-1/2}U(\beta _0,\eta _0)\nonumber \\&\quad =n^{-1/2}\sum _{i=1}^n \int _0^{\tau }\{Q_i(\beta _0,\eta _0)-\bar{Q}(t;\beta _0,\eta _0)\}dM^D_i(t)\nonumber \\&\qquad -n^{-1/2}\sum _{i=1}^n \int _0^{\tau } \{Q_i(\beta _0,\eta _0)-\bar{Q}(t;\beta _0,\eta _0)\}\Delta _i(t)\{\hat{V}_i-V_i\}\{\alpha _0(t)h(\beta _0'Z_i)\nonumber \\&\qquad +g(\eta _0'W_i)\}dt\nonumber \\&\quad =n^{-1/2}\sum _{i=1}^n \int _0^{\tau } \{Q_i(\beta _0,\eta _0)-\bar{q}(t)\}dM^D_i(t)\nonumber \\&\qquad -n^{-1/2}\sum _{i=1}^n \int _0^{\tau } \{Q_i(\beta _0,\eta _0)-\bar{q}(t)\}\Delta _i(t)\{\hat{V}_i-V_i\}\{\alpha _0(t)h(\beta _0'Z_i)\nonumber \\&\qquad +g(\eta _0'W_i)\}dt+o_p(1). \end{aligned}$$

(A.4)

Combing (A.3) and (A.4), we obtain

$$\begin{aligned} n^{-1/2}U(\beta _0,\eta _0)=n^{-1/2}\sum _{i=1}^n\xi _i+o_p(1), \end{aligned}$$

(A.5)

where

$$\begin{aligned} \xi _{i}=&\int _0^{\tau }\{Q_i(\beta _0,\eta _0)-\bar{q}(t)\}dM^D_i(t)\\&+\int _0^\tau \int \{q-\bar{q}(t)\} \frac{mI(y\ge t)}{\Lambda _0(y)e^{\gamma '_0 x}} b_i(y,x)\{\alpha _0(t)h(\beta _0'z)\\&+g(\eta _0'w)\} d P_2(q,z,w,x,y,m)dt, \end{aligned}$$

and $P_2(q,z,w,x,y,m)$ is the joint probability measure of $(Q_i(\beta _0,\eta _0), Z_i,W_i,X_i,Y_i,m_i)$.

Thus, by (A.5) and the multivariate central limit theorem, $n^{-1/2}U(\beta _0,\eta _0)$ converges in distribution to a zero-mean normal random vector with covariance matrix $\Sigma =E(\xi _i\xi _i')$. Note that $-n^{-1}\partial {U}(\beta _0, \eta _0)/\partial (\beta ',\eta ')$ converges in probability to A,  which is defined in condition (C3). By Taylor expansion theorem, we have that

$$\begin{aligned} n^{1/2}\left( \begin{array}{c} \hat{\beta }-\beta _0\\ \hat{\eta }-\eta _0 \end{array}\right) =A^{-1}n^{-1/2}U(\beta _0,\eta _0)+o_p(1), \end{aligned}$$

which converges in distribution to a joint normal distribution with mean zero and covariance matrix $A^{-1}\Sigma A'^{-1}.$ $\square$

Proof of Theorem 2

Note that

$$\begin{aligned} \hat{\mathcal A}_0(t;\beta ,\eta )=\int _0^t\frac{\sum _{i=1}^n\{dN^D_i(s)-\Delta _i(s)\hat{V}_ig(\eta 'W_i) ds\}}{\sum _{i=1}^n\Delta _i(s)\hat{V}_ih(\beta 'Z_i)}, \end{aligned}$$

and define

$$\begin{aligned} {\mathcal {A}}_0(t;\beta ,\eta )=\int _0^t\frac{E\{dN^D_i(s)-\Delta _i(s)V_ig(\eta 'W_i) ds\}}{E\{\Delta _i(s)V_ih(\beta 'Z_i)\}}. \end{aligned}$$

$\hat{\mathcal A}_0(t;\beta ,\eta )$ is a continuous functional of two processes because the denominator is bounded away from 0. The almost-sure convergence of the two processes can be established from the previous discussions. It can be shown that $\sup _{t\in [0,\tau ]}|\hat{\mathcal {A}}_0(t;\beta ,\eta )-{\mathcal {A}}_0(t;\beta ,\eta )|\rightarrow 0$ almost surely. Then the consistency of $\hat{\mathcal {A}}_0(t;\hat{\beta },\hat{\eta })$ for ${\mathcal {A}}_0(t)$ follows the strong consistency of $\hat{\beta }$ and $\hat{\eta }$ for $\beta _0$ and $\eta _0$.

A Taylor expansion of $\hat{\mathcal {A}}_0(t;\hat{\beta },\hat{\eta })$ about $\beta _0$ and $\eta _0$ gives

$$\begin{aligned} \hat{\mathcal {A}}_0(t;\hat{\beta },\hat{\eta })=\hat{\mathcal {A}}_0(t;\beta _0,\eta _0)+\frac{\partial \hat{\mathcal {A}}_0(t;\beta _t^*,\eta _t^*)}{\partial \beta }(\hat{\beta }-\beta _0)+\frac{\partial \hat{\mathcal {A}}_0(t;\beta _t^*,\eta _t^*)}{\partial \eta }(\hat{\eta }-\eta _0), \end{aligned}$$

(A.6)

where $\beta _t^*$ depends on t and lies on the line segment between $\hat{\beta }$ and $\beta _0$, $\eta _t^*$ depends on t and lies on the line segment between $\hat{\eta }$ and $\eta _0$. By a similar argument used earlier, we can show that ${\partial \hat{\mathcal {A}}_0(t;\beta _t^*,\eta _t^*)}/{\partial \beta }$ converges in probability to ${\partial {\mathcal {A}}_0(t;\beta _0,\eta _0)}/{\partial \beta }$, and ${\partial \hat{\mathcal {A}}_0(t;\beta _t^*,\eta _t^*)}/{\partial \eta }$ converges in probability to ${\partial {\mathcal {A}}_0(t;\beta _0,\eta _0)}/{\partial \eta }$ for $t\in [0,\tau ]$. Following Theorem 1,

$$\begin{aligned} n^{1/2}\left( \begin{array}{c} \hat{\beta }-\beta _0\\ \hat{\eta }-\eta _0 \end{array}\right) =n^{-1/2}\sum _{i=1}^nA^{-1}\xi _i+o_p(1), \end{aligned}$$

and from (A.6), we have

$$\begin{aligned}&n^{1/2}\left\{ \hat{\mathcal {A}}_0(t;\hat{\beta },\hat{\eta })-\hat{\mathcal {A}}_0(t;\beta _0,\eta _0)\right\} \nonumber \\&\quad =\frac{\partial {\mathcal {A}}_0(t;\beta _0,\eta _0)}{\partial \beta }n^{1/2}(\hat{\beta }-\beta _0)+\frac{\partial {\mathcal {A}}_0(t;\beta _0,\eta _0)}{\partial \eta }n^{1/2}(\hat{\eta }-\eta _0)+o_p(1)\nonumber \\&\quad =n^{-1/2}\sum _{i=1}^n\left( \frac{\partial {\mathcal {A}}_0(t;\beta _0,\eta _0)}{\partial \beta },\frac{\partial {\mathcal {A}}_0(t;\beta _0,\eta _0)}{\partial \eta }\right) A^{-1}\xi _i+o_p(1). \end{aligned}$$

(A.7)

Moreover, the functional delta method applied to $\hat{\mathcal {A}}_0(t;\beta _0,\eta _0)$ yields

$$\begin{aligned}&n^{1/2}\left\{ \hat{\mathcal {A}}_0(t;\beta _0,\eta _0)-{\mathcal {A}}_0(t;\beta _0,\eta _0)\right\} \nonumber \\&\quad = \int _0^t-\frac{n^{-1/2}\sum _{i=1}^n\left[ \Delta _i(s)\hat{V}_i h(\beta _0'Z_i)-E\{\Delta _i(s)V_ih(\beta _0'Z_i)\}\right] }{\left[ E\{\Delta _i(s)V_ih(\beta _0'Z_i)\}\right] ^2}E\left\{ dN_i^D(s)\right. \nonumber \\&\left. \qquad -\Delta _i(s)V_ig(\eta _0'W_i)ds\phantom {dN_i^D(s)}\right\} \nonumber \\&\qquad +\int _0^t\frac{n^{-1/2}\sum _{i=1}^n\left[ \left\{ dN_i^D(s)-\Delta _i(s)\hat{V}_ig(\eta _0'W_i)ds\right\} -E\left\{ dN_i^D(s)-\Delta _i(s)V_ig(\eta _0'W_i)ds\right\} \right] }{E\left\{ \Delta _i(s)V_ih(\beta _0'Z_i)\right\} }. \end{aligned}$$

(A.8)

From (A.3), it is easy to show that

$$\begin{aligned}&n^{-1/2}\sum _{i=1}^n\left[ \Delta _i(s)\hat{V}_i h(\beta _0'Z_i)-E\left\{ \Delta _i(s)V_ih(\beta _0'Z_i)\right\} \right] \nonumber \\&\quad =n^{-1/2}\sum _{i=1}^n\left[ \Delta _i(s)V_i h(\beta _0'Z_i)-E\left\{ \Delta _i(s)V_ih(\beta _0'Z_i)\right\} \right] \nonumber \\&\qquad +n^{-1}\sum _{i=1}^n\Delta _i(s)h(\beta _0'Z_i)\left[ n^{1/2}\left\{ \hat{V}_i-V_i\right\} \right] \nonumber \\&\quad =n^{-1/2}\sum _{i=1}^n\psi _{1i}(s)+o_p(1), \end{aligned}$$

(A.9)

where

$$\begin{aligned} \psi _{1i}(s)=&\Delta _i(s)V_i h(\beta _0'Z_i)-E\{\Delta _i(s)V_ih(\beta _0'Z_i)\}\\&-\int \frac{mI(y\ge s)}{\Lambda _0(y)e^{\gamma _0'x}}b_i(y,x)h(\beta _0'z)dP_3(z,x,y,m), \end{aligned}$$

and $P_3(z,x,y,m)$ is the joint probability measure of $(Z_i,X_i,Y_i,m_i)$. In a similar manner, from (A.3), it is easy to show that

$$\begin{aligned}&n^{-1/2}\sum _{i=1}^n\left[ \left\{ dN_i^D(s)-\Delta _i(s)\hat{V}_ig(\eta _0'W_i)ds\right\} -E\left\{ dN_i^D(s)-\Delta _i(s)V_ig(\eta _0'W_i)ds\right\} \right] \nonumber \\&\quad =n^{-1/2}\sum _{i=1}^n\left[ \left\{ dN_i^D(s)-\Delta _i(s)V_ig(\eta _0'W_i)ds\right\} -E\left\{ dN_i^D(s)\right. \right. \nonumber \\&\qquad \left. \left. -\Delta _i(s)V_ig(\eta _0'W_i)ds\phantom {dN_i^D(s)}\right\} \right] \nonumber \\&\qquad +n^{-1}\sum _{i=1}^n\Delta _i(s)g(\eta _0'W_i)\left[ n^{1/2}\{\hat{V}_i-V_i\}\right] ds\nonumber \\&\quad =n^{-1/2}\sum _{i=1}^n\psi _{2i}(s)ds+o_p(1), \end{aligned}$$

(A.10)

where

$$\begin{aligned} \psi _{2i}(s)=&\left[ \left\{ dN_i^D(s)-\Delta _i(s)V_ig(\eta _0'W_i)ds\right\} -E\left\{ dN_i^D(s)-\Delta _i(s)V_ig(\eta _0'W_i)ds\right\} \right] \\&-\int \frac{mI(y\ge s)}{\Lambda _0(y)e^{\gamma _0'x}}b_i(y,x)g(\eta _0'w)dP_4(w,x,y,m), \end{aligned}$$

and $P_{4}(w,x,y,m)$ is the joint probability measure of $(W_i,X_i,Y_i,m_i)$.

Thus, it follows from (A.8), (A.9) and (A.10) that

$$\begin{aligned}&n^{1/2}\left\{ \hat{\mathcal {A}}_0(t;\beta _0,\eta _0)-{\mathcal {A}}_0(t;\beta _0,\eta _0)\right\} \nonumber \\&\quad =n^{-1/2}\sum _{i=1}^n\int _0^t-\frac{\psi _{1i}(s)E\left\{ dN_i^D(s)-\Delta _i(s)V_ig(\eta _0'W_i)ds\right\} }{\left[ E\left\{ \Delta _i(s)V_ih(\beta _0'Z_i)\right\} \right] ^2}\nonumber \\&\qquad +\int _0^t\frac{\psi _{2i}(s)ds}{E\left\{ \Delta _i(s)V_ih(\beta _0'Z_i)\right\} }+o_p(1). \end{aligned}$$

(A.11)

By definition, $\hat{\mathcal {A}}_0(t;\hat{\beta },\hat{\eta })=\hat{\mathcal {A}}_0(t)$ and ${\mathcal {A}}_0(t;\beta _0,\eta _0)={\mathcal {A}}_0(t)$, it follows from (A.7) and (A.11) that

$$\begin{aligned} n^{1/2}\left\{ \hat{\mathcal {A}}_0(t)-{\mathcal {A}}_0(t)\right\} =&n^{-1/2}\sum _{i=1}^n\Psi _i(t)+o_p(1), \end{aligned}$$

where

$$\begin{aligned} \Psi _i(t)\!=&\left( \frac{\partial {\mathcal {A}}_0(t;\beta _0,\eta _0)}{\partial \beta },\frac{\partial {\mathcal {A}}_0(t;\beta _0,\eta _0)}{\partial \eta }\right) A^{-1}\xi _i\\&\!-\!\int _0^t\frac{\psi _{1i}(s)E\left\{ dN_i^D(s)-\Delta _i(s)V_ig(\eta _0'W_i)ds\right\} }{\left[ E\left\{ \Delta _i(s)V_ih(\beta _0'Z_i)\right\} \right] ^2} \!+\!\int _0^t\frac{\psi _{2i}(s)ds}{E\left\{ \Delta _i(s)V_ih(\beta _0'Z_i)\right\} }. \end{aligned}$$

Because $\Psi _i(t)$ is a linear combination of monotone processes with bounded second moments, the weak convergence of $n^{1/2}\{\hat{\mathcal {A}}_0(t)-{\mathcal {A}}_0(t)\}$ follows form example 2.11.16 of Vaart and Wellner (1996). $\square$

Appendix B: The choice of the weight function $Q_i(\beta ,\eta )$

If the baseline hazard function $\alpha _0(\cdot )$ is known, then the likelihood for $(\beta _0,\eta _0)$ is proportional to

$$\begin{aligned} \prod _{i=1}^n\left[ \left\{ \prod _{t\le \tau }\alpha _i(t)^{dN_i(t)}\right\} \exp \left\{ -\int _0^{\tau }\Delta _i(t)\alpha _i(t)dt\right\} \right] . \end{aligned}$$

The corresponding score function is

$$\begin{aligned} \sum _{i=1}^n\int _0^{\tau }\frac{\alpha _0(t)\dot{h}(\beta 'Z_i)Z_i}{\alpha _0(t)h(\beta 'Z_i) +g(\eta 'W_i)}dM_i^D(t;\beta ,\eta ), \end{aligned}$$

(B.1)

and

$$\begin{aligned} \sum _{i=1}^n\int _0^{\tau }\frac{\dot{g}(\eta 'W_i)W_i}{\alpha _0(t)h(\beta 'Z_i) +g(\eta 'W_i)}dM_i^D(t;\beta ,\eta ). \end{aligned}$$

(B.2)

In order to develop estimation procedures for $(\beta _0,\eta _0)$ when $\alpha _0(\cdot )$ is completely unspecified, (B.1) and (B.2) should be modified to eliminate $\alpha _0(\cdot )$ from the estimating functions. Thus, we replace the integrands in (B.1) and (B.2) by $Q_i(\beta ,\eta )$, which is a smooth $(p+q)$-vector-value function of $(Z_i, W_i, \beta , \eta ),$ and replace $\alpha _0(t) dt$ in $M_i^D(t;\beta ,\eta )$ by $\tilde{\mathcal A}_0(t;\beta ,\eta )$, which is the Aalen–Breslow type estimator for ${\mathcal A}_0(t)=\int _0^t\alpha _0(s)ds$ with known $v_i$ and $(\beta ,\eta )$, that is,

$$\begin{aligned} \tilde{\mathcal A}_0(t;\beta ,\eta )=\int _0^t\frac{\sum _{i=1}^n\{dN^D_i(s)-\Delta _i(s)v_i g(\eta 'W_i) ds\}}{\sum _{i=1}^n\Delta _i(s) v_ih(\beta 'Z_i)}. \end{aligned}$$

Then we obtain the following estimating equation for $(\beta _0,\eta _0)$:

$$\begin{aligned} \sum _{i=1}^n\int _0^\tau \left\{ Q_i(\beta ,\eta ) -\tilde{Q}(t;\beta ,\eta )\right\} \left[ dN^D_i(t)-\Delta _i(t)v_i g(\eta ' W_i)dt\right] =0, \end{aligned}$$

(B.3)

where

$$\begin{aligned} \tilde{Q}(t;\beta ,\eta )=\frac{\sum _{i=1}^n\Delta _i(t)v_i h(\beta 'Z_i)Q_i(\beta , \eta )}{\sum _{i=1}^n\Delta _i(t)v_i h(\beta 'Z_i)}. \end{aligned}$$

It can be checked that the estimating equation (B.3) is equivalent to the estimating equations on pages 5 and 6. Obviously, $Q_i(\beta ,\eta )$ in (7) will be a good approximation to the integrands in (B.1) and (B.2) if $\alpha _0(\cdot )$ is roughly constant and $g(\cdot )$ is small relative to $\alpha _0(\cdot )h(\cdot )$. In addition, putting (7) into (6), we obtain

$$\begin{aligned} U(\beta ,\eta )=\left( \begin{array}{c}U_{\beta }(\beta ,\eta )\\ U_{\eta }(\beta ,\eta ) \end{array}\right) , \end{aligned}$$

where

$$\begin{aligned} U_{\beta }(\beta ,\eta )= & {} \sum _{i=1}^n\int _0^{\tau }\left\{ \tilde{Z}_i(\beta ,\eta )-\bar{Z}(t;\beta ,\eta )\right\} \left[ dN^D_i(t)-\Delta _i(t)\hat{V}_ig(\eta ' W_i)dt\right] ,\\ U_{\eta }(\beta ,\eta )= & {} \sum _{i=1}^n\int _0^{\tau }\left\{ \tilde{W}_i(\beta ,\eta )-\bar{W}(t;\beta ,\eta )\right\} \left[ dN^D_i(t)-\Delta _i(t)\hat{V}_ig(\eta ' W_i)dt\right] , \end{aligned}$$

with

$$\begin{aligned} \bar{Z}(t;\beta ,\eta )=\frac{\sum _{i=1}^n\Delta _i(t)\hat{V}_ih(\beta 'Z_i)\tilde{Z}_i(\beta , \eta )}{\sum _{i=1}^n\Delta _i(t)\hat{V}_ih(\beta 'Z_i)}, \end{aligned}$$

and

$$\begin{aligned} \bar{W}(t;\beta ,\eta )=\frac{\sum _{i=1}^n\Delta _i(t)\hat{V}_ih(\beta 'Z_i)\tilde{W}_i(\beta , \eta )}{\sum _{i=1}^n\Delta _i(t)\hat{V}_ih(\beta 'Z_i)}. \end{aligned}$$

If $(Z_i',W_i')'=Z_i$, then $U_{\beta }$ becomes the estimating function of Huang and Wang (2004) under the multiplicative hazards model with a frailty:

$$\begin{aligned} \alpha _i(t) =v_i\{ \alpha _0(t)h(\beta _0'Z_i)\}. \end{aligned}$$

If $(Z_i',W_i')'=W_i$, then $U_{\eta }$ reduces to an ad hoc estimating function for additive hazards model with a frailty:

$$\begin{aligned} \alpha _i(t) =v_i\{ \alpha _0(t)+g(\eta _0' W_i)\}. \end{aligned}$$