Market power in bilateral oligopoly markets with non-expandable infrastructures

Abstract

We develop a novel model of price-fee competition in bilateral oligopoly markets with non-expandable infrastructures and costly transportation. The model captures a variety of real market situations and it is the continuous quantity version of the assignment game with indivisible goods on a fixed network. We define and characterize stable market outcomes. Buyers exclusively trade with the supplier with whom they achieve maximal bilateral joint welfare at prices equal to marginal costs. Maximal fees and the suppliers’ market power are restricted by the buyers’ credible threats to switch suppliers. Maximal fees also arise from a negotiation model that extends price competition to price-fee competition. Competition in both prices and fees necessarily emerges. It improves welfare compared to price competition, but buyers will not be better off. The minimal infrastructure achieving maximal aggregate welfare differs from the minimal network that protects buyers most.

1 Introduction

Modern oligopolistic markets often require building infrastructure with costly transportation on it. This can vary from costs of postal services when purchasing from online shops to physical infrastructure required to transport perfectly-divisible goods such as water, chemicals, electricity and natural gas. Often, in such contexts, payments for goods consist of two parts: a price per unit and a fee. Transportation costs may differ per supplier and per customer, for example tariffs for postal services typically distinguish between domestic and foreign destinations. Also, product modifications in the intermediate goods (B2B) markets to meet specifications set by heterogeneous customers can be treated as relation-specific transport cost. The importance of heterogeneous transportation costs in trade is not at par with standard microeconomics, with the notable exceptions of Hotelling (1929), Salop (1979), or Economides (1986) for markets with infinitely-many small customers and indivisible goods.

In our study, we analyze competition in both prices and fees in an oligopolistic market with a finite number of concentrated buyers and suppliers, who are both heterogeneous and exercise market power, on a given non-expandable infrastructure that transports some perfectly-divisible good.¹ Marginal costs of both production and transportation are constant and relation-specific. One aim is to analyze how oligopolistic competition with two-part pricing is affected by the infrastructure. Our results reflect real world patterns in e.g. natural gas production and its transportation industry, where physical links between buyers and sellers are required, or in intermediate goods markets, where B2B contracts play the role of links on an infrastructure.

We apply the Core concept to take into account the essence of market power or bargaining power, including threats to switch orders from one supplier to another.² We characterize all stable market outcomes and show that these are bilaterally efficient.³ Bilateral efficiency implies relation-specific marginal-cost pricing in order to realize the maximal bilateral joint welfare. Stable market outcomes are also Pareto efficient: the equilibrium quantities are the same as if all firms were price-takers. Thus, market power under oligopolistic competition in prices and fees does not necessarily cause distortions as opposed to oligopolistic competition in prices, where deadweight losses are unavoidable.⁴

The relation-specific fee distributes the joint welfare between the buyer and supplier. Zero fees yield maximal consumer surplus and higher fees reflect higher supply-side market power. In any stable market outcome, suppliers may trade with several buyers. Each buyer, however, prefers exclusive trade with his most-efficient (lowest-cost) supplier on the infrastructure in order to achieve maximal bilateral joint welfare. This exclusive trade implies that our model is equivalent to a many-to-one assignment game for which the Core has a lattice structure. Hence, the set of stable fees has a lattice structure and results for indivisible goods are also relevant in settings with continuous quantities.⁵ Obviously, exclusive trade makes each buyer vulnerable to market power exercised by his most-efficient supplier. Such market power, however, is limited by each buyer’s threat to trade with his second-efficient supplier. Therefore, a buyer’s maximal fee is bounded from above by the difference of the maximal bilateral joint welfare levels that can be achieved by trading with his most-efficient supplier and second-efficient supplier.

In our study, we model extreme market or bargaining power by one side of the market as a modified negotiation model similar to e.g. Section 6.2 in Roth and Sotomayor (1990) or Dam and Perez-Castrillo (2006). The modified negotiation model features simultaneous price-fee proposals by agents from one side of the market to all connected agents on the opposite side of the market and, if accepted, the agents who accept choose quantities. We are especially interested in the supply side making such proposals and compare the outcomes to those arising from oligopolistic (differentiated Bertrand) price competition. Suppliers propose marginal-cost pricing and the maximal stable fees, all relation-specific. Buyers accept the offer from their most-efficient supplier and demand the joint-welfare maximizing quantities. Compared to oligopolistic price competition, competition in both prices and fees improves aggregate joint welfare but buyers are not better off. When buyers propose, we have the relation-specific marginal-cost pricing and no (or zero) fees, which can be seen as the outcome under perfect competition.

We also demonstrate how assignment games as first proposed by Shapley and Shubik (1972) can be employed as a tool in competition economics to analyze complex and policy-relevant environments, market efficiency and buyers’ vulnerability to market power in spot-markets on infrastructures that cannot be expanded in the short run, such as infrastructure for natural gas. To address this we identify the minimal infrastructure that generates maximal aggregate joint welfare among all infrastructures. This infrastructure only requires that each buyer is linked to his most-efficient supplier. To reduce vulnerability of buyers to market power exercised by the supply side, we also identify the minimal infrastructure that generates the maximal aggregate consumer surplus among all infrastructures. This requires that each buyer is linked to his most-efficient and his second-most efficient supplier. In such setting, even though each buyer will never utilize one of his two links, the unused link needs to be present in order to have a credible threat of switching.

Our study is organized as follows. Section 2 outlines the model. Section 3 provides motivating examples. Oligopolistic competition in prices and fees with costly transportation on a non-expandable infrastructure is analyzed in Sect. 4. Section 5 concludes.

2 The model

Consider a market of some good with a finite set S of suppliers, $|S|\ge 1$, and a finite set B of buyers, $|B|\ge 1$. We denote an individual supplier as i and an individual buyer as j. The set of all agents is $N=S\cup B$, where the sets S and B are disjoint, i.e. $S\cap B=\emptyset$.

Bilateral trade requires infrastructure that links supplier i and buyer j . Without such a link, a pair of buyers and suppliers cannot trade. The link between supplier i and buyer j is denoted $ij\equiv \left( i,j\right) \in S\times B$, and often we call ij a pair. The set of all potential links ij is denoted by $g_{N}=\left\{ ij|ij\in S\times B\right\}$, which is an undirected graph. An infrastructure g on N is an arbitrary set of links $g\subseteq g_{N}$. The collection of all networks is denoted by $G_{N}=\left\{ g|g\subseteq g_{N}\right\}$. In what follows, we think of infrastructures as some non-expandable infrastructure inherited from the past whose building costs are sunk. For explanatory reasons, we assume that links are of unlimited capacity. Its operating and managing costs are assumed to be included in the variable transportation costs, which are defined below.

In this market, we keep track of trade flows between pairs of linked suppliers and buyers. For a given infrastructure $g\subseteq g_{N}$ and a pair $ij\in g$, the quantity $q_{ij}\ge 0$ denotes the flow of output from supplier i to buyer j. For convenience, we set $q_{ij}=0$ to represent the infeasibility of trade for any pair $ij\notin g$, and we denote the matrix of all trades on $g\subseteq g_{N}$ as $Q|g=\left( q_{ij}\right) _{ij\in S\times B}\in \mathbb {R} _{+}^{\left| S\times B\right| }$. Supplier i’s total production or quantity sold is $q_{i}=\sum _{j\in B:ij\in g}q_{ij}$. Production and shipping products within any pair takes place against constant marginal costs that depend upon the identity of the suppliers and buyers. Denote $c_{ij}\ge 0$,$\,ij\in g_{N}$, as the marginal costs of both production and transportation from supplier i to buyer j. Suppliers may sell their products to multiple buyers. Our framework assumes constant marginal costs and that available capacity is sufficient. This seems to reflect the current situation in the natural gas market and its transportation industry, where capacity is built in accordance with contracts that are signed in advance. Also the postal services market has similar contractual arrangements that remove the issue of insufficient capacity.

Given trades Q|g, we define the endogenous trade network $T\left( Q|g\right) \in g$ as all links $ij\in g$ with $q_{ij}>0$, i.e. all links with positive trade. Supplier i’s active customer network consists of those buyers with whom this supplier trades positive amounts (and with whom he is linked to).⁶ More specific, for supplier i, $T_{i}\left( Q|g\right) \subseteq B$ denotes supplier i’s set of active buyers j for which $q_{ij}>0$ on infrastructure g. By definition, this set may be empty if supplier i has no customers, a singleton in case he has only one customer or it contains multiple elements in case this supplier has many customers. Similarly, $T_{j}\left( Q|g\right) \subseteq S$ denotes buyer j’s set of active suppliers i for which $q_{ij}>0$ on infrastructure g.

Given trades Q|g, buyer j’s total consumption is $q_{j}=\sum _{i\in S:ij\in g}q_{ij}$, and this buyer has the quasi-linear utility function $u_{j}\left( q_{j}\right) +m_{j}$, where the function $u_{j}$ is increasing and strictly concave in $q_{j}$ and $m_{j}$ is monetary wealth.⁷ Competition in this market takes place through relation-specific prices $p_{ij}\ge c_{ij}$ and relation-specific fees $f_{ij}\ge 0$ for all pairs $ij\in g$. Joint pair-wise welfare within the pair $ij\in g$ can be expressed as the sum of i’s producer surplus $\left( p_{ij}-c_{ij}\right) q_{ij}+f_{ij}$ and j’s consumer surplus $u_{j}(q_{ij})-p_{ij}q_{ij}-f_{ij}$. The maximal joint welfare for the pair $ij\in g$ is given by $\max _{q_{ij}\ge 0}u_{j}(q_{ij})-c_{ij}q_{ij}$. Strict concavity ensures a unique joint welfare maximum for each possible link. For technical convenience, we assume:

Assumption 1

All $c_{ij}\ge 0$, $ij\in g_{N}$, are mutually different, and for each buyer $j\in S$, the function $u_{j}$ is increasing, continuously differentiable and strictly concave in $q_{j}$, $u_{j}\left( 0\right) =0$, and $u_{j}^{\prime }\left( 0\right) >\max _{i\in S}c_{ij}$.

Continuous differentiability and strict concavity of $u_{j}$, i.e. $u_{j}^{\prime }$ decreasing, implies that $u_{j}^{\prime }\left( q_{ij}\right) =c_{ij}$ has at most one solution. The assumption on the slope of $u_{j}$ at $q_{j}=0$ ensures that, in case of exclusive trade in the pair ij, such solution exists, buyer j consumes a positive quantity $q_{ij}$ and the maximal joint welfare without building costs is positive for each pair $ij\in g_{N}$. Mutually different $c_{ij}$ imply that each buyer can rank welfare maxima over the suppliers in S without indifferences, which allows to speak of the most-efficient and the second-efficient seller per buyer.

For the initial non-expandable infrastructure $g\subseteq g_{N}$, the maximal joint welfare associated with exclusive trade by buyer j with supplier i on link $ij\in g$, denoted $w_{g}\left( ij\right)$, is defined as

$$\begin{aligned} w_{g}\left( ij\right) =\left\{ \begin{array}{ll} \max _{q_{ij}\ge 0}\left[ u_{j}(q_{ij})-c_{ij}q_{ij}\right] , &{} \text {if } ij\in g,\\ 0, &{} \text {if }ij\notin g. \end{array}\right. \end{aligned}$$

(1)

Assumption 1 implies that $w_{g}\left( ij\right) >0$ for all $ij\in g$. Additionally, we assume:

Assumption 2

Given $g\subseteq g_{N}$, each buyer $j\in B$ has at least one link $i^{\prime }j\in g$ such that $w_{g}\left( i^{\prime }j\right) >0$, each supplier $i\in S$ has at least one link $ij^{\prime }\in g$ such that $w_{g}\left( ij^{\prime }\right) >0$.

This assumption ensures that each buyer and each seller has an incentive to trade on at least one link in $g\subseteq g_{N}$ (otherwise we could remove such agent from the model).

Finally, we denote the matrices of all prices and fees on $g\subseteq g_{N}$ as $P|g=\left( p_{ij}\right) _{ij\in S\times B}\in \mathbb {R} _{+}^{\left| S\times B\right| }$and $F|g=\left( f_{ij}\right) _{ij\in S\times B}\in \mathbb {R} ^{\left| S\times B\right| }$, respectively. The latter means we allow that links might be subsidized. We set $p_{ij}=u_{j}^{\prime }\left( 0\right) >c_{ij}$ and $f_{ij}=0$ to represent the infeasibility of trade for any pair $ij\notin g$, which makes $q_{ij}=0$ the optimal trade in $ij\notin g$ with supplier i’s producer surplus equal to zero.

3 Motivating examples

In this section, we discuss competition in both prices and fees. We start with the smallest market possible on a non-expandable infrastructure, namely the market that consists of a single supplier that is linked to a single buyer, referred to as supplier 1 and buyer 1. Quantity $q_{11}$ will be traded against price $p_{11}$ and fee $f_{11}$. Additionally, we set the constant marginal costs of production and transportation to $c_{11}=1$. Buyer 1 has utility function $10\sqrt{q_{11}}-p_{11}q_{11}-f_{11}$. Maximal joint welfare is 25. It is reached by setting the price $p_{11}$ equal to marginal costs and trading $q_{11}$ equal to 25 units. Such price implies that the producer surplus equals the fee $f_{11}$, and the consumer surplus is $25-f_{11}$. The fee divides joint maximal welfare within each pair.

Given that both the supplier and the buyer can act strategically in this market, negotiations will result in marginal-cost pricing $p_{11}=1$ and a fee $f_{11}\in \left[ 0,25\right]$. In case of a monopoly, the theory in Oi (1971) predicts that the supplier will extract the entire consumer surplus by setting the price $p_{11}=1$ and fee $f_{11}=25$. By reversing roles, in a monopsony the buyer will set the price $p_{11}=1$ and fee $f_{11}=0$.

Next, we expand the previous situation by introducing supplier 2 who is less efficient and has constant marginal costs of production and transportation $c_{21}=2$. Supplier 2’s price and fee are $p_{21}$ and $f_{21}$. The maximal joint welfare supplier 2 and buyer 1 can attain when linked is 12.5. It can be reached by setting the price $p_{21}$ equal to supplier 2’s marginal costs and trading $q_{21}$ equal to 6.25 units. Such price implies that supplier 2’s producer surplus equals his fee $f_{21}$, and the consumer surplus is $12.5-f_{21}$. Again, the fee redistributes the joint maximal welfare.

Next, we consider the case with both suppliers connected to the buyer. Given that both suppliers and the buyer can act strategically in this market, supplier 1 must take into account the presence of supplier 2 in negotiations on prices and fees. By negotiations, we envision some unmodeled negotiation process that will result in a Core solution. Since supplier 2 and buyer 1 can reach a joint welfare of 12.5 together, supplier 1 cannot extract more welfare from buyer 1 than $25-12.5=12.5$. So, negotiations will result in supplier 1’s price $p_{11}=c_{11}$ and fee $f_{11}\in \left[ 0,12.5\right]$, and supplier 2’s price $p_{21}=c_{21}$ and fee $f_{21}=0$. The theory in Oi (1971) can be easily extended to competition in prices and fees in this duopoly, if one considers the following price-fee-setting game: Simultaneously and independently suppliers set their price and fee combination, and then the buyer decides how much to demand from each supplier. Then, the unique equilibrium outcome supports the above prices and fees with $f_{11}=$ 12.5, and the buyer purchases 25 units from supplier 1 and nothing from supplier 2.⁸ Hence, this equilibrium outcome is Pareto efficient and more favorable for the buyer than the modified price-fee-setting game in the monopoly situation. This result differs from the standard duopoly where supplier 1 sets his price equal to supplier 2’s marginal costs to extract consumer surplus and fees are absent.⁹ So, the price-fee-setting game on a non-expandable infrastructure also explains the phenomenon of setting two-part tariffs in practice. By reversing the roles in a monopsony, the buyer will set $p_{11}=p_{21}=c_{11}$ and $f_{11}=f_{21}=0$, and supplier 1 will exclusively trade 25 units with buyer 1. Note that adding a third supplier, called supplier 3, with marginal costs above $c_{22}=2$ will not change the above market outcomes.

The example shows that from buyer 1’s perspective, the presence of the link to supplier 2 is a safeguard against supplier 1’s market power, yet this link will never be utilized for trade. The link with the third-efficient supplier 3 is not needed.¹⁰ This is a fundamental tension between the minimal infrastructure that maximizes social welfare from trade and the minimal infrastructure that minimizes the supply side’s market power. In this paper, we develop a theory that characterizes both such infrastructures and show that the former is included in the latter.

4 Competition on non-expandable infrastructures

In this section, we analyze oligopolistic competition in prices and fees on a non-expandable infrastructure. As the equilibrium concept, we modify the concept of a deviating (or blocking) coalition to the context of a perfectly divisible good and money on an infrastructure. We characterize the set of stable market outcomes and analyze strategic negotiation models that yield each side’s most preferred stable market outcome as the unique equilibrium outcome.¹¹

4.1 Competition in prices and fees

Market outcomes consist of prices, fees, and the quantities traded. A market outcome on a non-expandable infrastructure $g\subseteq g_{N}$ is defined as the triple $\left( P|g,F|g,Q|g\right)$. Therefore, each market outcome generates an endogenous trade network $T\left( Q|g\right) \in g$ of positive trades. The Core concept imposes that any market outcome on a non-expandable infrastructure is stable if no coalition of suppliers and buyers wants to break away and trade on their own. To put it differently, all coalitions of suppliers and buyers weakly prefer the market outcome to trading as a subgroup.

Formally, for coalition $C\subseteq N$ on infrastructure $g\subseteq g_{N}$, we define buyer j’s quantity purchased from suppliers in coalition C as

$$\begin{aligned} q_{j}\left( C|g\right) =\sum \limits _{i\in T_{j}\left( Q|g\right) \cap C}q_{ij}. \end{aligned}$$

For $C=N$, we write $q_{j}\left( N|g\right)$. Any stable market outcome $\left( P^{*}|g,F^{*}|g,Q^{*}|g\right)$ yields each agent a surplus. For supplier $i\in S$, the surplus consists of the revenues and fees collected from his active customer network $T_{i}\left( Q^{*}|g\right)$:

$$\begin{aligned} \sum \limits _{j\in T_{i}\left( Q^{*}|g\right) }\left[ (p_{ij}^{*}-c_{ij})q_{ij}^{*}+f_{ij}^{*}\right] . \end{aligned}$$

For buyer $j\in B$, the consumer surplus consists of the difference between his utility from purchasing $q_{j}^{*}\left( N|g\right)$ from his active supplier network $T_{j}\left( Q|g\right)$ and the expenditures and fees paid to his active suppliers:

$$\begin{aligned} u_{j}\left( q_{j}^{*}\left( N|g\right) \right) -\sum \limits _{i\in T_{j}\left( Q^{*}|g\right) }\left[ p_{ij}^{*}q_{ij}^{*}+f_{ij}^{*}\right] . \end{aligned}$$

Any market outcome yields each coalition in total a welfare that is equal to the sum of its members’ surpluses. Let $C=C_{S}\cup C_{B}$ be the partition of coalition $C\subseteq N$ into suppliers and buyers. The market outcome $\left( P^{*}|g,F^{*}|g,Q^{*}|g\right)$ yields coalition C on infrastructure $g\subseteq g_{N}$ the joint welfare:

$$\begin{aligned}&\sum _{i\in C_{S}}\left[ \sum \limits _{j\in T_{i}\left( Q^{*}|g\right) } \left[ (p_{ij}^{*}-c_{ij})q_{ij}^{*}+f_{ij}^{*}\right] \right] \nonumber \\&\quad +\sum _{j\in C_{B}}\left[ u_{j}\left( q_{j}^{*}\left( N|g\right) \right) -\sum \limits _{i\in T_{j}\left( Q^{*}|g\right) }\left[ p_{ij}q_{ij}^{*}+f_{ij}^{*}\right] \right] . \end{aligned}$$

(2)

This is coalition C’s joint welfare in case it stays and trades according to market outcome $\left( P^{*}|g,F^{*}|g,Q^{*}|g\right)$. Next, suppose coalition C considers to deviate from the above market outcome through the alternative market outcome $\left( P|g,F|g,Q|g\right)$. The surplus for any supplier in coalition C consists of the revenues and fees collected from his active customer network restricted to the buyers in coalition C, i.e. for supplier $i\in C_{S}\$these are all $j\in T_{i}\left( Q|g\right) \cap C_{B}$. Similarly, the consumer surplus of buyer $j\in C_{B}$ consists of the difference between his utility from purchasing $q_{j}\left( C|g\right)$ from his active suppliers in C, i.e. all $i\in T_{j}\left( Q|g\right) \cap C_{S}$, and the revenues and fees paid to these active suppliers in C. Since market outcome $\left( P|g,F|g,Q|g\right)$ yields each coalition a joint welfare that is equal to the sum of its members’ surpluses, deviating coalition C’s joint welfare is given by:

$$\begin{aligned}&\sum _{i\in C_{S}}\left[ \sum \limits _{j\in T_{i}\left( Q|g\right) \cap C_{B}} \left[ (p_{ij}-c_{ij})q_{ij}+f_{ij}\right] \right] \nonumber \\&\quad +\sum _{j\in C_{B}}\left[ u_{j}\left( q_{j}\left( C|g\right) \right) -\sum \limits _{i\in T_{j}\left( Q|g\right) \cap C_{S}}\left[ p_{ij}q_{ij}+f_{ij}\right] \right] . \end{aligned}$$

(3)

The main difference between (2) and (3) is that if a coalition stays it will trade internally in C and externally of its coalition in N, and if it deviates as a deviating coalition it will only trade internally. Deviating is profitable only if such restriction can be compensated by the surpluses from internal trades within the coalition. The market outcome is stable if every conceivable deviation is unprofitable. Given the joint welfare of deviating and non-deviating coalitions, we are ready to define stability of market outcomes.

Definition 3

Market outcome $\left( P^{*}|g,F^{*}|g,Q^{*}|g\right)$ on a non-expandable infrastructure $g\subseteq g_{N}$ is stable if the following condition holds:

$$\begin{aligned} \text {For all coalitions }C\subseteq N\text { and all }\left( P|g,F|g,Q|g\right) :(2) \ge (3) . \end{aligned}$$

(4)

Condition (4) expresses the idea that deviating coalitions are unprofitable, and it is a reformulation of Core stability for cooperative games in characteristic function form.

4.2 Characterization of stable market outcomes

The characterization of stable market outcomes requires the definition of a buyer’s most-efficient and second-(most-)efficient supplier on the infrastructure, which will be defined in terms of the maximal joint welfare within pairs of suppliers and buyers. For $g\subseteq g_{N}$, we define buyer j’s most-efficient supplier $\alpha _{j}\left( g\right) \in S$ on the infrastructure g as the supplier on g with whom j can attain his largest maximal joint welfare:

$$\begin{aligned} w_{g}\left( \alpha _{j}\left( g\right) j\right) \ge w_{g}\left( ij\right) ,\quad \text { for all }i\in S:ij\in g. \end{aligned}$$

(5)

Since maximal joint welfare is related to the most-efficient supplier in terms of marginal costs, we might alternatively define $\alpha _{j}\left( g\right)$ as the supplier for whom $c_{\alpha _{j}\left( g\right) j}=\min _{i\in S:ij\in g}c_{ij}$, but (5) captures the key insight needed in Sect. 5. Buyer j’s most-efficient supplier $\alpha _{j}\left( g\right)$ is uniquely defined if buyer j is linked through g to one or more suppliers. A buyer’s second-efficient supplier is defined similarly. For $g\subseteq g_{N}$, buyer j’s second-efficient supplier $i\in S$ on the infrastructure g is the supplier $\beta _{j}\left( g\right)$ on g with whom j attains his second maximal joint welfare:

$$\begin{aligned} w_{g}\left( \beta _{j}\left( g\right) j\right) \ge w_{g}\left( ij\right) ,\quad \text {for all }i\in S\backslash \left\{ \alpha _{j}\left( g\right) \right\} :ij\in g. \end{aligned}$$

(6)

Buyer j’s second-efficient supplier $\beta _{j}\left( g\right)$ is uniquely defined if buyer j is linked through g to two or more suppliers in S. Otherwise, and similar as before, we impose the convention that $\beta _{j}\left( g\right) =0$, marginal cost $c_{0j}=u_{j}^{\prime }\left( 0\right)$, and the pair 0j has maximal joint welfare $w_{g}\left( 0j\right) =0$. By definition, either $c_{\beta _{j}\left( g\right) j}=\min _{i\in S\backslash \left\{ \alpha _{j}\left( g\right) \right\} :ij\in g}c_{ij}$ or $c_{0j}$.

We have the following characterization. All proofs are deferred to the appendix.

Proposition 4

Market outcome $\left( P^{*}|g,F^{*}|g,Q^{*}|g\right)$ on a non-expandable infrastructure $g\subseteq g_{N}$ is stable if and only if for all $ij\in g:$

$$\begin{aligned} \begin{array}{lll} p_{\alpha _{j}\left( g\right) j}^{*}=c_{\alpha _{j}\left( g\right) j}, &{} p_{ij}^{*}\ge c_{ij}, &{} \text {if }i\ne \alpha _{j}\left( g\right) ,\\ f_{\alpha _{j}\left( g\right) j}^{*}\in \left[ 0,w_{g}(\alpha _{j}\left( g\right) j)-w_{g}(\beta _{j}\left( g\right) j)\right] , &{} f_{ij}^{*}\ge 0, &{} \text {if }i\ne \alpha _{j}\left( g\right) , \\ q_{\alpha _{j}\left( g\right) j}^{*}=\arg \max _{q_{\alpha _{j}\left( g\right) j}\ge 0}u_{j}(q_{\alpha _{j}\left( g\right) j})-c_{\alpha _{j}\left( g\right) j}q_{\alpha _{j}\left( g\right) j}, &{} q_{ij}^{*}=0, &{} \text {if }i\ne \alpha _{j}\left( g\right) . \end{array} \end{aligned}$$

(7)

For $i\in S$ and $j\in B$, supplier i’s active customers network $T_{i}\left( Q^{*}|g\right) =\left\{ j\in B|i=\alpha _{j}\left( g\right) \right\}$, and buyer j’s active supplier network $T_{j}\left( Q^{*}|g\right) =\left\{ \alpha _{j}\left( g\right) \right\}$.

From the proof it follows that multiple prices and fees can occur in stable market outcomes on any link $ij\in g$ that will not be utilized for trade. Suppliers on those links know that even at their lowest acceptable prices and fees, i.e. $p_{ij}^{*}=c_{ij}$ and $f_{ij}^{*}=0$, their products are too expensive from the perspective of buyer j. Therefore, their prices and fees do not matter.

Proposition 4 implies a very precise prediction of stable market outcomes. Each buyer exclusively trades with his most-efficient supplier on the infrastructure against a price that equals this supplier’s marginal costs and pays a positive fee. This makes buyer j vulnerable to market power exercised by his most-efficient supplier. Such market power is limited by the buyer’s threat to trade with his second-efficient supplier $\beta _{j}\left( g\right) \in S\cup \left\{ 0\right\}$ on infrastructure g . Since supplier $\beta _{j}\left( g\right)$’s current profit from zero trades with buyer j is zero, buyer j can seduce supplier $\beta _{j}\left( g\right)$ to trade and guarantee himself a consumer surplus of $w_{g}(\beta _{j}\left( g\right) j)$. This limits the market power of the most-efficient supplier $\alpha _{j}\left( g\right)$ in extracting consumer surplus from the pair $\alpha _{j}\left( g\right) j\in g$, because supplier $\alpha _{j}\left( g\right)$ must make sure that buyer j enjoys at least a consumer surplus of $w_{g}(\beta _{j}\left( g\right) j)$ through the link $\beta _{j}\left( g\right) j$. The most-efficient supplier’s fee is therefore bounded from above by the difference between $w_{g}(\alpha _{j}\left( g\right) j)$ and $w_{g}(\beta _{j}\left( g\right) j)$.

Under marginal cost of production and transportation, a supplier’s producer surplus is equal to the sum of profits per individual link. Supplier i’s profit that can be attributed to the link $ij\in g$ for buyer $j\in T_{i}\left( Q^{*}|g\right)$ is equal to $(p_{ij}^{*}-c_{ij})q_{ij}^{*}+f_{ij}^{*}=f_{ij}^{*}\ge 0$, with weak inequality if $T_{i}\left( Q^{*}|g\right) \ne \emptyset$ and equality otherwise. Supplier i’s aggregate profit is equal to the sum of these fees, i.e. $\mathop {{\textstyle \sum }}_{j\in T_{i}\left( Q^{*}|g\right) }f_{ij}^{*}$, and only suppliers who are some buyer’s most-efficient supplier trade. Then, it is impossible that trade in a link is subsidized, because $f_{ij}^{*}<0$ would be an incentive for supplier i to refuse trade. Supplier i’s active customer network consists of all buyers for whom this supplier is the most-efficient supplier.

We investigate the upper bound on the most-efficient supplier’s fee for several special cases. In case j is only linked to a single supplier, then $\beta _{j}\left( g\right) =0$ and $w_{g}(0j)=0$ imply $f_{\alpha _{j}\left( g\right) j}^{*}\le w_{g}(\alpha _{j}\left( g\right) j)$. The absence of a second-efficient supplier imposes no threat to supplier $\alpha _{j}\left( g\right)$ and hence no limitation to its market power. In case j is linked to two or more suppliers, the difference in marginal costs between the most-efficient and the second-efficient supplier matters. If this difference is relatively large, then $w_{g}(\beta _{j}\left( g\right) j)$ will be relatively small compared to $w_{g}(\alpha _{j}\left( g\right) j)$, and the limiting effect of the threat to switch suppliers will be relatively small. On the other hand, if both the marginal costs of the most-efficient and of the second-efficient supplier are relatively close to each other, then $w_{g}(\beta _{j}\left( g\right) j)$ will be close to $w_{g}(\alpha _{j}\left( g\right) j)$ and the presence of the second-efficient supplier has a substantial dampening effect on the most-efficient supplier’s fee. In case marginal costs coincide, which we exclude for convenience, then $w_{g}(\beta _{j}\left( g\right) j)=w_{g}(\alpha _{j}\left( g\right) j)$ and the most-efficient supplier’s fee must be zero. This implies that for industries with almost identical costs structures the equilibrium fees will be small.

The lower bound on all most-efficient suppliers’ fees also has an interesting interpretation. In that case the fee $f_{ij}^{*}=0$ for all $ij\in g$. It can be interpreted as the generalization of the competitive equilibrium for markets on a non-expandable infrastructure in the sense that all suppliers follow marginal-cost pricing at zero fees. Given different constant marginal costs, the competitive equilibrium implies relation-specific prices, and zero profits for all suppliers, whether active or not. Obviously, relation-specific prices are Pareto efficient and a uniform price per supplier is not.

Proposition 4 implies that the supply side prefers high fees among the set of stable market outcomes and the demand side prefers low fees from this set. This links our result to previous results in assignment games with indivisible goods. The reason is that our model is equivalent to a many-to-one assignment game, a particular case of the many-to-many assignment game in Sotomayor (1999, 2002, 2007), for which the set of setwise-stable and Core allocations coincide and both form non-empty complete lattices.

4.3 Strategic negotiations

Next, we analyze a strategic negotiation model in case the supply side holds all market power. We characterize the unique equilibrium and relate it to the suppliers’ most-preferred stable market outcome. We also relate this equilibrium to the Bertrand equilibrium of standard oligopolistic price competition.

As an important benchmark model, we first consider standard Bertrand price competition. In this model, each supplier sets possibly relation-specific prices to all the buyers he is connected with. Then, each buyer decides how much to purchase from each supplier against the prices offered to him.¹² Formally, each supplier $i\in S$ proposes prices $\left( p_{ij}\right) _{j\in B:ij\in g}$, and then each buyer $j\in B$ chooses his purchases $q_{ij}\ge 0$. This model is a well defined game in extensive form for which subgame perfect equilibrium is the appropriate concept, which we call the Bertrand equilibrium. Dependent upon the infrastructure, buyer j may face none, one or several suppliers. In case buyer j is connected to a single supplier, then this supplier can exercise monopoly power on his link with buyer j. To capture this case on a non-expandable infrastructure $g\subseteq g_{N}$, we denote buyer j’s set of connected suppliers on g as $S_{j}\left( g\right)$. In case $\left| S_{j}\left( g\right) \right| =1$, denote $p_{\alpha _{j}\left( g\right) j}^{M}$ as the standard monopoly price that buyer j’s single supplier would charge. We establish the following equilibrium paths, the supporting strategy profile can be found in the proof.

Proposition 5

Consider the Bertrand price competition model on a non-expandable infrastructure $g\subseteq g_{N}$. In any Bertrand equilibrium, the suppliers propose

$$\begin{aligned} \begin{array}{llll} \hat{p}_{\alpha _{j}\left( g\right) j}=p_{\alpha _{j}\left( g\right) j}^{M}, &{} &{} &{} \text {if }\left| S_{j}\left( g\right) \right| =1, \\ \hat{p}_{\alpha _{j}\left( g\right) j}=p_{\alpha _{j}\left( g\right) j}^{M}, &{} \hat{p}_{\beta _{j}\left( g\right) j}\ge c_{\beta _{j}\left( g\right) j}, &{} \hat{p}_{ij}\ge c_{ij}\text { otherwise,} &{} \text {if }\left| S_{j}\left( g\right) \right| \ge 2\text { and }p_{\alpha _{j}\left( g\right) j}^{M}<c_{\beta _{j}\left( g\right) j},\\ \hat{p}_{\alpha _{j}\left( g\right) j}=c_{\beta _{j}\left( g\right) j}, &{} \hat{p}_{\beta _{j}\left( g\right) j}=c_{\beta _{j}\left( g\right) j}, &{} \hat{p}_{ij}\ge c_{ij}\text { otherwise,} &{} \text {if }\left| S_{j}\left( g\right) \right| \ge 2\text { and }p_{\alpha _{j}\left( g\right) j}^{M}\ge c_{\beta _{j}\left( g\right) j}, \end{array} \end{aligned}$$

and, on the equilibrium path, the buyers purchase

$$\begin{aligned} \begin{array}{ll} \hat{q}_{\alpha _{j}\left( g\right) j}=\arg \max _{q_{\alpha _{j}\left( g\right) j}\ge 0}u_{j}(q_{\alpha _{j}\left( g\right) j})-\hat{p}_{\alpha _{j}\left( g\right) j}q_{\alpha _{j}\left( g\right) j},&\hat{q}_{ij}=0 \text { otherwise.} \end{array} \end{aligned}$$

This result is an extension of the standard monopoly model and standard Bertrand oligopoly with mutually different marginal costs. The multiplicity of Bertrand equilibria is nonessential in the sense that the multiple equilibrium prices for the third-efficient supplier, the fourth-efficient supplier and so on all result in a unique Bertrand equilibrium outcome: Buyer $j\in B$ exclusively trades an amount of $\hat{q} _{\alpha _{j}\left( g\right) j}$ with his most-efficient supplier $\alpha _{j}\left( g\right) \in S\cup \left\{ 0\right\}$ against the Bertrand equilibrium price $\hat{p}_{\alpha _{j}\left( g\right) j}$. In a monopoly or in case the cost advantage of the most-efficient supplier is sufficiently large compared with the second-efficient supplier, then the most-efficient supplier can exercise monopoly power over buyer j and set the classic monopoly price $p_{\alpha _{j}\left( g\right) j}^{M}$. Otherwise, the presence of at least one competing supplier limits the most-efficient supplier’s price to $c_{\beta _{j}\left( g\right) j}$. In the last case, buyer j’s consumer surplus is equal to $w_{g}(\beta _{j}\left( g\right) j)$ , and the profit for buyer j’s most-efficient supplier on their link is given by $(c_{\beta _{j}\left( g\right) j}-c_{\alpha _{j}\left( g\right) j}) \hat{q}_{\alpha _{j}\left( g\right) j}$. Of course, the Bertrand equilibrium is inefficient.

We now address competition in both prices and fees. Recall our reinterpretation of fees as the price for a contract that allows buyer $j\in B$ to purchase unlimited amounts of the good from supplier $i\in S$ against price $p_{ij}$. In the negotiation model, we let each supplier propose such contracts to all the buyers he is connected with. So, each supplier sets possibly relation-specific prices and fees to all such buyers. Formally, each supplier $i\in S$ proposes prices $\left( p_{ij}\right) _{j\in B:ij\in g}$ and fees $\left( f_{ij}\right) _{j\in B:ij\in g}$, and then each buyer $j\in B$ decides how much to trade with whom, where we interpret $q_{ij}>0$ as buyer j’s acceptance of supplier i’s contract and $q_{ij}=0$ as rejectance. Also this negotiation model is a well defined game in extensive form, and by equilibrium we mean subgame perfect equilibrium. We establish the following equilibrium paths, the supporting strategy profile can be found in the proof.

Proposition 6

Let $g\subseteq g_{N}$ be a non-expandable infrastructure. For the unique equilibrium in the negotiation model where the supply side proposes, and the demand side decides how much to trade with whom, it holds that suppliers propose

$$\begin{aligned} \begin{array}{llll} p_{\alpha _{j}\left( g\right) j}^{*}=c_{\alpha _{j}\left( g\right) j}, &{} p_{\beta _{j}\left( g\right) j}^{*}=c_{\beta _{j}\left( g\right) j}, &{} p_{ij}^{*}\ge c_{ij}, &{} \text {if }i\ne \alpha _{j}\left( g\right) ,\beta _{j}\left( g\right) ,\\ f_{\alpha _{j}\left( g\right) j}^{*}=w_{g}(\alpha _{j}\left( g\right) j)-w_{g}(\beta _{j}\left( g\right) j), &{} f_{\beta _{j}\left( g\right) j}^{*}=0, &{} f_{ij}^{*}\ge 0, &{} \text {if }i\ne \alpha _{j}\left( g\right) ,\beta _{j}\left( g\right) , \end{array} \end{aligned}$$

and, on the equilibrium path, the buyers purchase

$$\begin{aligned} \begin{array}{llll} q_{\alpha _{j}\left( g\right) j}^{*}=\arg \max _{q_{\alpha _{j}\left( g\right) j}\ge 0}u_{j}(q_{\alpha _{j}\left( g\right) j})-c_{\alpha _{j}\left( g\right) j}q_{\alpha _{j}\left( g\right) j},&q_{\beta _{j}\left( g\right) j}^{*}=0,&q_{ij}^{*}=0,&\text {if }i\ne \alpha _{j}\left( g\right) . \end{array} \end{aligned}$$

Again, the multiplicity in prices and fees is inessential. In equilibrium, $f_{\beta _{j}\left( N|g\right) j}^{*}>0$ cannot hold under competition, because supplier $\alpha _{j}\left( N|g\right)$ is then tempted to charge a fee slightly above the upper bound $w_{g}\left( \alpha _{j}\left( N|g\right) j\right) -w_{g}\left( \beta _{j}\left( N|g\right) j\right)$ knowing that buyer j will not switch. Also, $p_{\beta _{j}\left( N|g\right) j}^{*}>c_{\beta _{j}\left( N|g\right) j}$ allows additional out-of-equilibrium extraction of consumer surplus.

Proposition 6 implies that competition in prices and fees must emerge endogenously if suppliers have the possibility to set fees. To see this, consider a buyer with several competing suppliers that limit the most-efficient supplier’s Bertrand equilibrium price of Proposition 5 to $c_{\beta _{j}\left( g\right) j}$. Recall that buyer j’s consumer surplus is $w_{g}(\beta _{j}\left( g\right) j)$, and most-efficient supplier $\alpha _{j}\left( g\right)$’s profit of this link is $(c_{\beta _{j}\left( g\right) j}-c_{\alpha _{j}\left( g\right) j})\hat{q}_{\alpha _{j}\left( g\right) j}$. The sum of this profit plus the positive deadweight loss is equal to $w_{g}(\alpha _{j}\left( g\right) j)-w_{g}(\beta _{j}\left( g\right) j)$, which implies the upper bound on the most-efficient supplier’s fee has a nice graphical interpretation. By adopting marginal-cost pricing and setting a positive fee, the most-efficient supplier extracts the Bertrand equilibrium profit plus the deadweight loss through the fee. Hence, each most-efficient supplier will choose the latter and competition in prices and fees must emerge endogenously. Only in case $w_{g}(\alpha _{j}\left( g\right) j)=w_{g}(\beta _{j}\left( g\right) j)$, which would imply equal marginal costs, fees will be zero. It is also possible to show that consumers are weakly worse off under competition in prices and fees than under Bertrand price competition.¹³ This generalizes insights of Oi (1971).

Also, Proposition 6 shows that oligopolistic competition in prices and fees is Pareto efficient, because all suppliers adopt marginal-cost pricing. Our intuition is that suppliers offer marginal-cost-pricing contracts with unrestricted supply. Then contract prices equal fees while buyers only need a single contract, i.e. an “indivisible” item. This interpretation immediately translates into many-to-one assignment games. A similar result is also obtained in other papers of matching with competition for contracts modeled as an assignment game. For example, Dam and Perez-Castrillo (2006) analyze high-effort contracts with endogenous investments between principals and agents. They also show that stable market outcomes are Pareto efficient.

Our results differ from the literature on two-part pricing in oligopolistic markets that all have a complete infrastructure in our terminology. Harrison and Kline (2001) assume homogenous agents on both sides, constant marginal costs and competition in quantities and fees. They report marginal-cost pricing and positive homogeneous fees. We attribute their result of positive fees to quantity competition as opposed to the zero fees under price competition in our setting. Calem and Spulber (1984) assume two groups of buyers and two suppliers of close, but not necessarily perfect, substitutes, say pasta and rice. They implicitly impose that consumers from both buyer groups pay the same price and fee, i.e., uniform prices and fees. Under all these assumptions, uniform prices exceed marginal costs and the maximal uniform fees are set by the threat of exclusive trade with the other supplier.¹⁴

In some markets, it is the demand side that has most or all market power. For example, in the airline industry buyers such as Boeing and Airbus appear to be more powerful than their suppliers of particular parts of the aircraft. Obviously, such markets can be captured by reversing the roles of the agents in the previous negotiation model.

4.4 Buyer protection

In this section, we compare different non-expandable infrastructures and we pose the question which of these infrastructures provide maximal consumer protection. Recall that non-expandable infrastructures have sunk building costs, and we therefore compare different infrastructures by their effects on the set of stable market outcomes on $w_{g}$.

The complete infrastructure $g=g_{N}$ is a special case in which each supplier is connected to each buyer. It represents the standard notion of competition in a market in which everyone can trade with everyone else. Under sunk building costs, the complete infrastructure enables the highest joint welfare from trade, which is $\max _{g\subseteq g_{N}}\sum _{j\in B}w_{g}(\alpha _{j}\left( g\right) j)=\max _{g\subseteq g_{N}}\sum _{j\in B}\max _{i\in S}w_{g}\left( ij\right)$. So, the entire market achieves a level of maximal joint welfare of $\sum _{j\in B}w_{g}(\alpha _{j}\left( g_{N}\right) j)$. Note that the minimal non-expandable infrastructure that achieves the same level of welfare only consists of the links between each buyer and his most-efficient supplier. We define the latter infrastructure as the non-expandable infrastructure $g_{E}\subseteq g_{N}$ given by $g_{E}=\left\{ \text { }\alpha _{j}\left( g_{N}\right) j\text { }\left| \text { }j\in B,\alpha _{j}\left( g_{N}\right) \in S\right. \right\}$.

The issue is that on the non-expandable infrastructure $g_{E}$, buyers are unprotected against market power, because it lacks any of the links between each buyer and his second-efficient supplier. The question to be answered is what non-expandable infrastructure serves buyers best in protecting their interests? As a criterion, we propose to maximize the worst-case for the buyers’s consumer surpluses over all non-expandable infrastructures, which would be their consumer surplus with the second-efficient supplier on such infrastructure. Formally, in non-expandable infrastructure $g\subseteq g_{N}$ the buyers can guarantee themselves $\sum _{j\in B}w_{g}(\beta _{j}\left( g\right) j)$. It is this criterion that should be maximized to optimally protect buyers. Obviously, the complete infrastructure guarantees the highest consumer surplus from trade, because $\max _{g\subseteq g_{N}}\sum _{j\in B}w_{g}(\beta _{j}\left( g\right) j)=\sum _{j\in B}\max _{i\in S}w_{g}\left( \beta _{j}\left( g_{N}\right) j\right)$. Note that the minimal non-expandable infrastructure $g\subseteq g_{N}$ that achieves maximal protection links buyer j to his most-efficient supplier $\alpha _{j}\left( g_{N}\right) \in S$ and his second-efficient supplier $\beta _{j}\left( g_{N}\right) \in B$. Without the link between $\alpha _{j}\left( g_{N}\right)$ and j, both buyer j’s most-efficient supplier and his second-efficient supplier would change, destroying some joint welfare and some guaranteed consumer surplus. We define the minimal non-expandable infrastructure $g_{M}\subseteq g_{N}$ that achieves maximal buyer protection under sunk building costs as $g_{M}=\left\{ \text { }\alpha _{j}\left( g_{N}\right) j,\beta _{j}\left( g_{N}\right) j\text { }\left| \text { }j\in B,\alpha _{j}\left( g_{N}\right) ,\beta _{j}\left( g_{N}\right) \in S\right. \right\}$.

The set of stable market outcomes under non-expandable infrastructure $g_{M}$ , or any non-expandable infrastructure $g\subseteq g_{N}$ containing $g_{M}$ , is equal to the set of stable outcomes under the complete infrastructure $g_{N}$. This minimal infrastructure is rather sparse. Without any of the links $\beta _{j}\left( g_{N}\right) j$, the set of stable market outcomes would enlarge for all non-expandable infrastructures $g\subseteq g_{N}$ containing $g_{E}$. Formally, every infrastructure $g\subseteq g_{N}$ such that $g\supseteq g_{E}$ and $g\nsupseteq g_{M}$ has a larger set of stable market outcomes than the complete infrastructure $g_{N}$. The reason is that some of the upper bounds on the most-efficient suppliers’ fees increase. Removing any of the links $\alpha _{j}\left( g_{N}\right) j$ has two negative effect: both the maximal joint welfare on the infrastructure and the maximal attainable consumer surplus drop. To summarize this discussion, we have established:

Proposition 7

Non-expandable infrastructure $g_{M}$ is the minimal non-expandable infrastructure $g\subseteq g_{N}$ that achieves maximal consumer protection. Moreover, all non-expandable infrastructures $g\subseteq g_{N}$ that contain $g_{M}$ also achieve this, which includes $g=g_{N}$.

This result also implies that the set of stable market outcomes for all non-expandable infrastructures $g\subseteq g_{N}$ that contain $g_{M}$ is the smallest set of stable market outcomes over all infrastructures that contain $g_{E}$, which includes the complete infrastructure $g_{N}$. For all infrastructures that contain $g_{E}$ but only partly overlap with $g_{M}$, the set of stable market outcomes is larger.

4.5 Example

In this subsection, we discuss the extension of the motivating example of Sect. 3 by adding a second buyer.¹⁵ Consider a market with two suppliers of e.g. natural gas, supplier 1 being efficient and supplier 2 inefficient, and two heterogeneous buyers, buyer 1 having a higher marginal willingness to pay (say high-income country Germany) than buyer 2 (say middle-income country Spain). Supplier 1’s constant joint marginal costs of production and transportation are $c_{11}=c_{12}=1$, and those for supplier 2 are $c_{21}=c_{22}=2$. Buyer 1 has utility function $10\sqrt{ q_{11}+q_{21}}-p_{11}q_{11}-f_{11}-p_{21}q_{21}-f_{21}$, and buyer 2 has $8 \sqrt{q_{12}+q_{22}}-p_{12}q_{12}-f_{12}-p_{22}q_{22}-f_{22}$. Then, $w_{g}\left( 11\right) =25$, $w_{g}\left( 21\right) =12.5$, $w_{g}\left( 12\right) =16$ and $w_{g}\left( 22\right) =8$. In infrastructure A of Fig. 1, which is $g_{E}$, both buyers are only connected to their most-efficient suppliers on the complete infrastructure $g_{N}$, which is supplier 1. Then, $0\le f_{11}\le w_{g}\left( 11\right) =25$ and $0\le f_{12}\le w_{g}\left( 12\right) =16$, and the maximal fees correspond to monopoly market power. In contrast, in infrastructure D of Fig. 1, which is $g_{M}$, both buyers are connected to their most-efficient supplier, i.e. 1, and second-most-efficient supplier, i.e. 2, on the complete infrastructure $g_{N}$. Note that for this example $g_{M}=g_{N}$. Then, under D the range of fees is smaller $0\le f_{11}\le w_{g}\left( 11\right) -w_{g}\left( 21\right) =12.5$ and $0\le f_{12}\le w_{g}\left( 12\right) -w_{g}\left( 22\right) =8$, and the maximal fees are limited due to increased competition.

Fig. 1

The single supplier infrastructure in Case III is $g_{E}$, Case IV and V represent duopoly markets, and the complete infrastructure of Case VI coincides with $g_{M}$

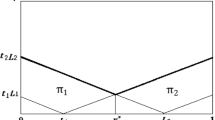
For a graphical illustration of fees and consumer surpluses in relation to non-expandable infrastructures, we can consider all possible infrastructures with two suppliers and two buyers that contain infrastructure $g_{E}$. The most relevant infrastructures are given in Fig. 1, the infrastructures $g_{E}$ (Case A) and $g_{M}$ (Case D), and both intermediate infrastructures (B and C). The graphical representation of the set of stable market outcomes for these non-expandable infrastructures is given in Fig. 2. The largest diamond-shaped area represents the set of stable market outcomes in case of the single supplier infrastructure $g_{E}$. The effect of having access to second-efficient suppliers, i.e. infrastructure $g_{E}$ augmented with one of the links 21 or 22 or both, are illustrated by the two lines that run through the largest diamond-shape area. Link 21 is associated with the line whose sum is 12.5, and link 22 with 8. In case both these links are present, we are in infrastructure $g_{M}$ (Case D) and the smallest diamond-shaped area corresponds to the smallest set of stable market outcomes on infrastructures that contain $g_{E}$. Although the links with supplier 2 (Qatar or Nigeria) will not be utilized, their presence reduces the maximal fee $f_{11}$ charged by supplier 1 (Russia or Algeria) to buyer 1 from 25 to 12.5 and the maximal fee $f_{12}$ charged to buyer 2 from 16 to 8.

Fig. 2

Different areas represent several sets of stable market outcomes of Example, where buyer i’s consumer surplus is denoted $CS_{i}$, $i=1,2$. The line $f_{21}+CS_{1}=12.5$ illustrates the effect of the link 21, and $f_{22}+CS_{2}=8$ the link 22

5 Concluding remarks

We consider price-fee competition in bilateral oligopolies with perfectly-divisible goods, concentrated heterogeneous agents on both sides, non-expandable infrastructures, and constant marginal costs. We study stable market outcomes that reflect that both sides possess market power. For every non-expandable infrastructure, stable market outcomes are both bilaterally and Pareto efficient because suppliers set unit prices equal to the relation-specific marginal costs. Relation-specific fees split bilateral joint welfare and fees implicitly reflect the suppliers’ market power. Each buyer exclusively trades with his most-efficient supplier on the infrastructure and the maximal relation-specific fee is limited by the buyer’s threat to switch to his second-efficient supplier on the infrastructure. Competition in prices and fees necessarily emerges from differentiated Bertrand price competition, as do marginal-cost pricing and maximal fees. Although welfare improves compared to Bertrand price competition, the buyers will not be better off.

Our results quantify the countervailing power hypothesis in Galbraith (1952): Buyers have countervailing power that can restrain the suppliers’ market power. In our study, buyers’ bargaining position improves if the threat to switch from one supplier to another yields a larger maximal-attainable consumer surplus. We quantify this insight for any non-expandable infrastructure and show that the supply side’s market power is decreasing in the number of arbitrary links a buyer has. We also characterize the minimal infrastructure that protects buyers the most and identify for each buyer two links that are crucial in protecting him from the supply side’s market power.

Future research could relax several assumptions made in this study. First of all, every supplier can produce any quantity demanded and each link can accommodate any demand. Capacity constraints can be easily included, but as each buyer may need to trade with more than one supplier, a many-to-many assignment game arises. Another important direction is to further investigate the application of assignment games to market competition for “indivisible” contracts, e.g. marginal-cost-pricing contracts with unlimited supply analyzed in this study or the high-effort contracts between principals and agents in Dam and Perez-Castrillo (2006).

Appendix: Proofs

Proof of Proposition 4

For any coalition C, cancelling common terms in (2)–(4) implies

$$\begin{aligned}&\sum _{j\in C_{B}}\left[ u_{j}\left( q_{j}^{*}\left( N|g\right) \right) -\sum \limits _{i\in T_{j}\left( Q|g\right) }c_{ij}q_{ij}^{*}\right] \nonumber \\&\quad \ge \max _{Q|g}\sum _{j\in C_{B}}\left[ u_{j}\left( q_{j}\left( C|g\right) \right) -\sum \limits _{i\in T_{j}\left( Q|g\right) \cap C}c_{ij}q_{ij}\right] , \end{aligned}$$

(8)

i.e. for coalition C the sum of joint welfare in the stable market outcome is at least the maximal sum of joint welfare in the coalition C. Since all $c_{ij}$ are mutually different, the maximum is achieved only if each buyer $j\in C_{B}$ exclusively deals with his most-efficient supplier $i\in C_{S}$ on g, which we denote $\alpha _{j}\left( C|g\right)$ in this proof including $C=N$ for which we already defined $\alpha _{j}\left( g\right)$. Combined with (1) for $ij\in g$, the right-hand side of (8) is equal to

$$\begin{aligned} \max _{Q|g}\sum _{j\in C_{B}}\left[ u_{j}(q_{\alpha _{j}\left( C|g\right) j})-c_{\alpha _{j}\left( C|g\right) j}q_{\alpha _{j}\left( C|g\right) j} \right] =\sum _{j\in C_{B}}w_{g}\left( \alpha _{j}\left( C|g\right) j\right) . \end{aligned}$$

So, for each coalition $C\subseteq N$, (8) is equivalent to

$$\begin{aligned} \sum _{j\in C_{B}}\left[ u_{j}\left( q_{j}^{*}\left( N|g\right) \right) -\sum \limits _{i\in T_{j}\left( Q|g\right) }c_{ij}q_{ij}^{*}\right] \ge \sum _{j\in C_{B}}w_{g}\left( \alpha _{j}\left( C|g\right) j\right) , \end{aligned}$$

and for $C=N$, (8) is equivalent to

$$\begin{aligned} \sum _{j\in B}\left[ u_{j}\left( q_{j}^{*}\left( N|g\right) \right) -\sum \limits _{i\in T_{j}\left( Q|g\right) }c_{ij}q_{ij}^{*}\right] =\sum _{j\in B}w_{g}\left( \alpha _{j}\left( N|g\right) j\right) . \end{aligned}$$

The previous arguments also imply that the latter equality holds at $C=N$ if and only if

$$\begin{aligned} \sum _{j\in B}\left[ u_{j}\left( q_{j}^{*}\left( N|g\right) \right) -\sum \limits _{i\in T_{j}\left( Q|g\right) }c_{ij}q_{ij}^{*}\right] =\max _{Q|g}\sum _{j\in B}\left[ u_{j}\left( q_{j}\left( N|g\right) \right) -\sum \limits _{i\in T_{j}\left( Q|g\right) }c_{ij}q_{ij}\right] . \end{aligned}$$

Hence, for every buyer $j\in B$ it must hold that $q_{\alpha _{j}\left( N|g\right) j}^{*}$ maximizes $u_{j}(q_{\alpha _{j}\left( g\right) j})-c_{\alpha _{j}\left( g\right) j}q_{\alpha _{j}\left( g\right) j}$, and $q_{ij}^{*}=0$ for all $i\in S\backslash \left\{ \alpha _{j}\left( N|g\right) \right\}$. By assumption 1, $q_{\alpha _{j}\left( N|g\right) j}^{*}>0$. Then also, $q_{j}^{*}\left( N|g\right) =q_{\alpha _{j}\left( N|g\right) j}^{*}$, buyer i’s set of active suppliers is $T_{j}\left( Q|g\right) =\left\{ \alpha _{j}\left( N|g\right) \right\}$, and $u_{j}\left( q_{j}^{*}\left( N|g\right) \right) -\sum \nolimits _{i\in T_{j}\left( Q|g\right) }c_{ij}q_{ij}^{*}=w_{g}\left( \alpha _{j}\left( N|g\right) j\right)$. This establishes $Q^{*}|g$.

Next, since trade takes place against prices $P^{*}|g$, $Q^{*}|g$ can be attained through such trade if and only if $p_{\alpha _{j}\left( N|g\right) j}^{*}=c_{\alpha _{j}\left( N|g\right) j}$ and $p_{ij}^{*}\ge c_{ij}$ for all $i\in S\backslash \left\{ \alpha _{j}\left( N|g\right) \right\}$. The last condition in Definition 3 sets $p_{ij}^{*}=c_{ij}$ for every link with $q_{ij}^{*}=0$, and this is the case for every $i\ne \alpha _{j}\left( N|g\right)$. Since all $c_{ij}$ are mutually different, $p_{ij}^{*}>c_{\alpha _{j}\left( N|g\right) j}$ for all $i\in S\backslash \left\{ \alpha _{j}\left( N|g\right) \right\}$.

Finally, we derive $F^{*}|g$. Given $Q^{*}|g$, consider supplier i and his active customer network $T_{i}\left( Q^{*}|g\right)$, that is $\left\{ i\right\} \cup T_{i}\left( Q^{*}|g\right)$. Suppose for $\hat{ \jmath }\in T_{i}\left( Q^{*}|g\right)$, that supplier i and part of his trade network want to break away by excluding trade with buyer $\hat{ \jmath }$, that is consider coalition $C=\left\{ i\right\} \cup T_{i}\left( Q^{*}|g\right) \backslash \left\{ \hat{\jmath }\right\}$. Given $P^{*}|g$, supplier i’s producer surplus is equal to $f_{i\hat{\jmath }}^{*}+\sum \limits _{j\in T_{i}\left( Q^{*}|g\right) \backslash \left\{ \hat{ \jmath }\right\} }f_{ij}^{*}$. This implies that (2) is equivalent to

$$\begin{aligned} f_{i\hat{\jmath }}^{*}+\sum _{j\in T_{i}\left( Q^{*}|g\right) \backslash \left\{ \hat{\jmath }\right\} }\left[ u_{j}\left( q_{ij}^{*}\right) -c_{ij}q_{ij}^{*}\right] =f_{i\hat{\jmath }}^{*}+\sum _{j\in T_{i}\left( Q^{*}|g\right) \backslash \left\{ \hat{\jmath }\right\} }w_{g}\left( ij\right) . \end{aligned}$$

Hence, (4) imposes

$$\begin{aligned} f_{i\hat{\jmath }}^{*}+\sum _{j\in T_{i}\left( Q^{*}|g\right) \backslash \left\{ \hat{\jmath }\right\} }w_{g}\left( ij\right) \ge \sum _{j\in T_{i}\left( Q^{*}|g\right) \backslash \left\{ \hat{\jmath } \right\} }w_{g}\left( ij\right) \quad \Longleftrightarrow \quad f_{i\hat{ \jmath }}^{*}\ge 0. \end{aligned}$$

Given $Q^{*}|g$, consider buyer $\hat{\jmath }\in B$, his second-efficient supplier $\beta _{\hat{\jmath }}\left( N|g\right)$, and this supplier’s active customer network $T_{\beta _{\hat{\jmath }}\left( N|g\right) }\left( Q^{*}|g\right)$, that is $C=\left\{ \hat{\jmath } ,\beta _{\hat{\jmath }}\left( N|g\right) \right\} \cup T_{\beta _{\hat{\jmath } }\left( N|g\right) }\left( Q^{*}|g\right)$. Then, (4) imposes

$$\begin{aligned}&u_{\hat{\jmath }}(q_{\alpha _{\hat{\jmath }}\left( N|g\right) \hat{\jmath } }^{*})-c_{\alpha _{\hat{\jmath }}\left( N|g\right) \hat{\jmath }}q_{i\hat{ \jmath }}^{*}-f_{\alpha _{\hat{\jmath }}\left( N|g\right) \hat{\jmath } }^{*}\ +\sum _{j\in T_{\beta _{\hat{\jmath }}\left( N|g\right) }\left( Q^{*}|g\right) }w_{g}\left( ij\right) \\&\quad \ge w_{g}\left( \beta _{\hat{\jmath }}\left( N|g\right) \hat{\jmath } \right) +\sum _{j\in T_{\beta _{\hat{\jmath }}\left( N|g\right) }\left( Q^{*}|g\right) }w_{g}\left( ij\right) , \end{aligned}$$

Since $u_{\hat{\jmath }}(q_{\alpha _{\hat{\jmath }}\left( N|g\right) \hat{ \jmath }}^{*})-c_{\alpha _{\hat{\jmath }}\left( N|g\right) \hat{\jmath } }q_{i\hat{\jmath }}^{*}=w_{g}\left( \alpha _{\hat{\jmath }}\left( N|g\right) \hat{\jmath }\right)$, this condition is equivalent to

$$\begin{aligned} f_{\alpha _{\hat{\jmath }}\left( N|g\right) \hat{\jmath }}^{*}\le w_{g}\left( \alpha _{\hat{\jmath }}\left( N|g\right) \hat{\jmath }\right) -w_{g}\left( \beta _{\hat{\jmath }}\left( N|g\right) \hat{\jmath }\right) \le w_{g}\left( \alpha _{\hat{\jmath }}\left( N|g\right) \hat{\jmath }\right) . \end{aligned}$$

The prices $p_{ij}^{*}\ge c_{ij}$ and the fees $f_{ij}^{*}\ge 0$ for every link with $q_{ij}^{*}=0$ are unrestricted, and this is the case for every $i\ne \alpha _{j}\left( N|g\right)$. $\square$

Proof of Proposition 5

Given the history of proposed prices P|g, we define for each connected buyer $j\in B$ the lowest proposed price as $\bar{p}_{\hat{\imath } j}\left( P|g\right) =\min _{i\in S:ij\in g}\left\{ p_{ij}\right\}$, where $\hat{\imath }$ denotes an arbitrary supplier who set such lowest price (which might be $\alpha _{j}\left( g\right)$). Given history P|g, buyer $j\in B$ purchases

$$\begin{aligned} q_{\alpha _{j}\left( g\right) j}\left( P|g\right)= & {} \left\{ \begin{array}{ll} \arg \max _{q_{\alpha _{j}\left( g\right) j}\ge 0}u_{j}(q_{\alpha _{j}\left( g\right) j})-p_{\alpha _{j}\left( g\right) j}q_{\alpha _{j}\left( g\right) j}, &{} \text {if }p_{\alpha _{j}\left( g\right) j}\le \bar{p}_{\hat{\imath } j}\left( P|g\right) , \\ 0, &{} \text {otherwise,} \end{array}\right. \\ q_{\hat{\imath }j}\left( P|g\right)= & {} \left\{ \begin{array}{ll} \arg \max _{q_{\hat{\imath }j}\ge 0}u_{j}(q_{\hat{\imath }j})-p_{\hat{\imath } j}q_{\hat{\imath }j},\ &{} \text {if }p_{\alpha _{j}\left( g\right) j}>\bar{p}_{\hat{\imath }j}\left( P|g\right) , \\ 0, &{} \text {otherwise,} \end{array} \right. \\ q_{ij}\left( P|g\right)= & {} 0,\qquad i\ne \alpha _{j}\left( g\right) ,\hat{ \imath }. \end{aligned}$$

On the equilibrium path, $\hat{\imath }=\alpha _{j}\left( g\right)$ or $\beta _{j}\left( g\right)$, buyer j purchases $q_{\alpha _{j}\left( g\right) j}(\hat{P}|g)=\hat{q}_{\alpha _{j}\left( g\right) j}>0$ and $q_{\beta _{j}\left( g\right) j}\left( P|g\right) =0$, which is in accordance to the endogenous tie-breaking rule in Simon and Zame (1990). Verification that the suppliers’ strategies and the buyers’ strategies form a subgame perfect equilibrium strategy profile goes as follows: On and off the equilibrium path, buyer j always purchases the optimal quantity from a supplier that offers the lowest price, so his strategy is optimal for every history. If $\hat{p}_{\alpha _{j}\left( g\right) j}=p_{\alpha _{j}\left( g\right) j}^{M}$ , then supplier $\alpha _{j}\left( g\right)$’s producer surplus is maximal and this supplier does not want to deviate. If $\hat{p}_{\alpha _{j}\left( g\right) j}=c_{\beta _{j}\left( g\right) j}$, then the deviation $p_{\alpha _{j}\left( g\right) j}>c_{\beta _{j}\left( g\right) j}$ implies that buyer j will exclusively trade with $\beta _{j}\left( g\right)$ against the price $\hat{p}_{\beta _{j}\left( g\right) j}=c_{\beta _{j}\left( g\right) j}$ , and supplier $\alpha _{j}\left( g\right)$ looses buyer j as his customer which reduces his positive equilibrium profits on the link $\alpha _{j}\left( g\right) j$ to zero. Also, the lower deviating price $p_{\alpha _{j}\left( g\right) j}<\hat{p}_{\alpha _{j}\left( g\right) j}$ reduces supplier $\alpha _{j}\left( g\right)$’s profits. Hence, $\hat{p}_{\alpha _{j}\left( g\right) j}$ is optimal given the other strategies. Since the other suppliers do not trade whether or not they deviate by setting other prices, they do not have any profitable deviating price. This establishes equilibrium.

There do not exist other Bertrand equilibrium outcomes. To see this, in any Bertrand equilibrium buyers always purchase from suppliers who set the lowest price. For $\left| S_{j}\left( g\right) \right| =1$, $\alpha _{j}\left( g\right) =1$ and standard monopoly pricing implies $\hat{p} _{1j}=p_{1j}^{M}$ is the unique price. Next, consider $\left| S_{j}\left( g\right) \right| =2$. Renumber the suppliers in S such that $S_{j}\left( g\right) =\left\{ 1,2\right\}$, $\alpha _{j}\left( g\right) =1$ and $\beta _{j}\left( g\right) =2$. If $p_{1j}^{M}<c_{2j}$, it is optimal for supplier 1 to act as a standard monopolist, and supplier 2 would make negative profits by undercutting this price. Then, only $\hat{p} _{1j}=p_{1j}^{M}$ and any $\hat{p}_{2j}\ge c_{2j}$ can be equilibrium prices. Next, $p_{1j}^{M}\ge c_{2j}$. Then, modification of the arguments for the first-price auction with mutually different valuations in Simon and Zame (1990), establishes that in any Bertrand equilibrium we must have $\hat{p}_{1j}=\hat{p}_{2j}=c_{2j}$ and buyer j exclusively trades with supplier 1, i.e. $q_{1j}(\hat{P}|g)=\hat{q}_{1j}$ and $q_{2j}(\hat{P}|g)=0$ . Finally, for $\left| S_{j}\left( g\right) \right| \ge 3$, it is straightforward to show that both $\hat{p}_{\alpha _{j}\left( g\right) j}= \hat{p}_{\beta _{j}\left( g\right) j}\le \min _{i\in S\backslash \left\{ \alpha _{j}\left( g\right) ,\beta _{j}\left( g\right) \right\} :ij\in g}c_{ij}$, and then the arguments for $\left| S_{j}\left( g\right) \right| =2$ apply to suppliers $\alpha _{j}\left( g\right)$ and $\beta _{j}\left( g\right)$. The other $p_{ij}\ge c_{ij}$ are unrestricted. $\square$

Proof of Proposition 6

Given history h of proposed prices P|g and fees F|g, for each connected buyer $j\in B$ define the proposed pair of price and fee from which this buyer can achieve the largest consumer surplus as $\bar{p}_{\hat{ \imath }j}\left( P|g\right)$ and $\bar{f}_{\hat{\imath }j}\left( P|g\right)$ , where $\hat{\imath }$ denotes an arbitrary supplier who sets such combination (which might be $\alpha _{j}\left( g\right)$). Given history h , buyer $j\in B$ exclusively trades with supplier $\alpha _{j}\left( g\right)$ the quantity $q_{\alpha _{j}\left( g\right) j}\left( h\right) =\arg \max _{q_{\alpha _{j}\left( g\right) j}\ge 0}u_{j}(q_{\alpha _{j}\left( g\right) j})-p_{\alpha _{j}\left( g\right) j}q_{\alpha _{j}\left( g\right) j}-f_{\alpha _{j}\left( g\right) j}$ if

$$\begin{aligned} \max _{q_{\alpha _{j}\left( g\right) j}\ge 0}u_{j}(q_{\alpha _{j}\left( g\right) j})-p_{\alpha _{j}\left( g\right) j}q_{\alpha _{j}\left( g\right) j}-f_{\alpha _{j}\left( g\right) j}\ge \max _{i\in S:ij\in g}\max _{q_{ij}\ge 0}\left[ u_{j}(q_{ij})-p_{ij}q_{ij}-f_{ij}\right] , \end{aligned}$$

and $q_{\alpha _{j}\left( g\right) j}\left( P|g\right) =0$ otherwise. Buyer j exclusively purchases from supplier $\hat{\imath }$ the quantity $q_{\hat{ \imath }j}\left( h\right) =\arg \max _{q_{\hat{\imath }j}\ge 0}u_{j}(q_{\hat{ \imath }j})-p_{\hat{\imath }j}q_{\hat{\imath }j}$ if

$$\begin{aligned} \max _{q_{\alpha _{j}\left( g\right) j}\ge 0}u_{j}(q_{\alpha _{j}\left( g\right) j})-p_{\alpha _{j}\left( g\right) j}q_{\alpha _{j}\left( g\right) j}-f_{\alpha _{j}\left( g\right) j}<\max _{i\in S:ij\in g}\max _{q_{ij}\ge 0} \left[ u_{j}(q_{ij})-p_{ij}q_{ij}-f_{ij}\right] , \end{aligned}$$

and $q_{\hat{\imath }j}\left( P|g\right) =0$ otherwise. Buyer j always purchase $q_{ij}\left( P|g\right) =0$ from the other suppliers. On the equilibrium path, buyer j purchases $q_{\alpha _{j}\left( g\right) j}^{*}\equiv q_{\alpha _{j}\left( g\right) j}(h^{*})$, where history $h^{*}$ denotes the proposed $P^{*}|g$ and $F^{*}|g$. This is in accordance to the endogenous tie-breaking rule in Simon and Zame (1990). Verification that the suppliers’ strategies and the buyers’ strategies form a subgame perfect equilibrium strategy profile is as follows: For any history h on and off the equilibrium path, buyer j always purchases the optimal quantity from one of the suppliers from which he achieves the maximal consumer surplus dependent upon the history h, so his strategy is optimal. Since $p_{\alpha _{j}\left( g\right) j}^{*}=c_{\alpha _{j}\left( g\right) j}$ and $f_{\alpha _{j}\left( g\right) j}^{*}=w_{g}(\alpha _{j}\left( g\right) j)-w_{g}(\beta _{j}\left( g\right) j)$, then any deviation $p_{\alpha _{j}\left( g\right) j}\ge c_{\alpha _{j}\left( g\right) j}$ and $f_{\alpha _{j}\left( g\right) j}\ge f_{\alpha _{j}\left( g\right) j}^{*}$ with at least one strict inequality implies that buyer j will exclusively trade with $\beta _{j}\left( g\right)$ against $p_{\beta _{j}\left( g\right) j}^{*}=c_{\beta _{j}\left( g\right) j}$ and $f_{\beta _{j}\left( g\right) j}^{*}=0$, and supplier $\alpha _{j}\left( g\right)$ looses buyer j as his customer which reduces his equilibrium profit on the link $\alpha _{j}\left( g\right) j$ from $f_{\alpha _{j}\left( g\right) j}^{*}>0$ to zero. Also, the lower deviating fee $f_{\alpha _{j}\left( g\right) j}<f_{\alpha _{j}\left( g\right) j}^{*}$ reduces supplier $\alpha _{j}\left( g\right)$’s profits. Hence, $p_{\alpha _{j}\left( g\right) j}^{*}$ and $f_{\alpha _{j}\left( g\right) j}^{*}$ are optimal given the other strategies. Since the other suppliers do not trade independent of the prices and fees they set, there does not exist any profitable deviating price and fee combination for any of them. This establishes equilibrium.

There do not exist other equilibrium outcomes. To see this, in any equilibrium buyers always purchase from suppliers who set a price and fee combination from which buyers can achieve a maximal consumer surplus. For $\left| S_{j}\left( g\right) \right| =1$, we renumber such that $S_{j}\left( g\right) =\left\{ 1\right\}$. Since $\beta _{j}\left( g\right) =0$ and $w_{g}\left( 0j\right) =0$, we have that $p_{1j}^{*}=c_{1j}$ and $f_{1j}^{*}=w_{g}\left( 1j\right)$ are optimal by the results in Oi (1971). Next, consider $\left| S_{j}\left( g\right) \right| =2$. Renumber the suppliers in S such that $S_{j}\left( g\right) =\left\{ 1,2\right\}$, $\alpha _{j}\left( g\right) =1$ and $\beta _{j}\left( g\right) =2$. There cannot exist an equilibrium in which buyer j exclusively trades with supplier 1 against $p_{1j}^{*}>c_{1j}$ and

$$\begin{aligned} f_{1j}^{*}=\max _{q_{1j}\ge 0}\left[ u_{j}(q_{1j})-p_{1j}^{*}q_{1j} \right] -w_{g}\left( 2j\right) <w_{g}\left( 1j\right) -w_{g}\left( 2j\right) , \end{aligned}$$

because then supplier 1 can increase his profits arbitrarily close to $w_{g}\left( 1j\right) -w_{g}\left( 2j\right)$ by the deviation $p_{1j}=c_{1j}$ and $f_{1j}=w_{g}\left( 1j\right) -w_{g}\left( 2j\right) -\varepsilon$, for sufficiently small $\varepsilon >0$. So, in any equilibrium, supplier 1 can secure $w_{g}\left( 1j\right) -w_{g}\left( 2j\right)$. Also, an equilibrium with $p_{1j}^{*}>c_{1j}$ and $f_{1j}^{*}>\max _{q_{1j}\ge 0}\left[ u_{j}(q_{1j})-p_{1j}^{*}q_{1j} \right] -w_{g}\left( 2j\right)$ is impossible. So, $p_{1j}^{*}=c_{1j}$ in any equilibrium. Next, there cannot exist an equilibrium with $p_{2j}^{*}>c_{2j}$ and $f_{2j}^{*}=0$ either. To see this, first note that then buyer j would exclusively trade with supplier 1 against $p_{1j}^{*}=c_{1j}$ and

$$\begin{aligned} f_{1j}^{*}=w_{g}\left( 1j\right) -\max _{q_{2j}\ge 0}\left[ u_{j}(q_{2j})-p_{2j}^{*}q_{2j}\right] >w_{g}\left( 1j\right) -w_{g}\left( 2j\right) . \end{aligned}$$

Exclusive trade is dictated by the insights in Simon and Zame (1990). Supplier 2 will have a profit of zero, and could obtain a positive profit by setting $p_{2j}=c_{2j}$ and $f_{2j}=\frac{1}{2}\left( f_{1j}^{*}-\left[ w_{g}\left( 1j\right) -w_{g}\left( 2j\right) \right] \right) >0$, a contradiction. Finally, there cannot exist an equilibrium with $p_{2j}^{*}=c_{2j}$ and $f_{2j}^{*}>0$, because then buyer j would exclusively trade with supplier 1 at the fee $f_{1j}^{*}=w_{g}\left( 1j\right) -w_{g}\left( 2j\right) +f_{2j}^{*}$ (exclusive trade again by Simon and Zame 1990). Supplier 2 will have a profit of zero, and could obtain a positive profit by decreasing his fee to $f_{\beta _{j}\left( g\right) j}=\frac{1}{2}f_{\beta _{j}\left( g\right) j}^{*}>0$. So, in any equilibrium $p_{2j}^{*}=c_{2j}$ and $f_{2j}^{*}=0$. Since also $p_{1j}^{*}=c_{1j}$ is necessary, and supplier 1 can secure a profit of $w_{g}\left( 1j\right) -w_{g}\left( 2j\right)$, the unique equilibrium fee must be $f_{1j}^{*}=w_{g}\left( 1j\right) -w_{g}\left( 2j\right)$. By Simon and Zame (1990), this can only be supported by exclusive trade between buyer j and supplier 1. Finally, for $\left| S_{j}\left( g\right) \right| \ge 3$, only suppliers $\alpha _{j}\left( g\right)$ and $\beta _{j}\left( g\right)$ matter in the argument, the other suppliers’ $p_{ij}\ge c_{ij}$ and $f_{ij}\ge 0$ are unrestricted. $\square$