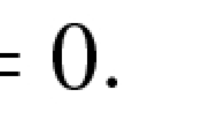Skip to main content
SpringerLink
Log in

The positive consequence of strategic manipulation in indivisible good allocation

  • Original Paper
  • Published:
International Journal of Game Theory Aims and scope Submit manuscript

Abstract

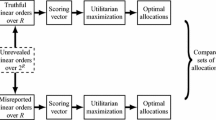
It is well known that any decision efficient, budget balanced, and envy-free mechanism for allocating a single object with transfers is vulnerable to manipulation. In this paper we examine whether the possible manipulations can have a serious impact on the outcome. Specifically, we examine which allocations are realized in the direct revelation game of any rule satisfying certain normative properties. For this class of rules we show that decision efficient, budget balanced, and envy-free allocations are the only ones realized through an ɛ-Nash equilibrium for any sufficiently small ɛ > 0.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Alcalde J (1996) Implementation of stable solutions to marriage problems. J Econ Theory 69: 240–254

    Article  Google Scholar 

  • Alkan A, Demange G, Gale D (1991) Fair allocation of indivisible goods and criteria of justice. Econometrica 59: 1023–1039

    Article  Google Scholar 

  • Ando K, Kato M, Ohseto S (2008) Strategy-proof and symmetric allocation of an indivisible good. Math Soc Sci 55: 14–23

    Google Scholar 

  • Beviá C (1996) Identical preferences lower bound solution and consistency in economies with indivisible goods. Soc Choice Welf 13: 113–126

    Article  Google Scholar 

  • Beviá C (2001) Manipulation games in economies with indivisible goods. mimeo, Universitat Autònoma de Barcelona

  • Bochet O, Sakai T (2007) Strategic manipulations of multi-valued solutions in economies with indivisibilities. Math Soc Sci 53: 53–68

    Article  Google Scholar 

  • Bochet O, Sakai T (2008) Preference manipulations lead to the uniform rule. mimeo, University of Bern and Yokohama National University

  • Clarke E (1971) Multi-part pricing of public goods. Public Choice 11: 17–33

    Article  Google Scholar 

  • Foley D (1967) Resource allocation and the public sector. Yale Econ Essays 7: 45–98

    Google Scholar 

  • Fujinaka Y, Sakai T (2007a) The manipulability of fair solutions in allocation of an indivisible object with money. J Public Econ Theory 9: 993–1011

    Article  Google Scholar 

  • Fujinaka Y, Sakai T (2007b) Maskin monotonicity in economies with indivisible goods with money. Econ Lett 94: 253–258

    Article  Google Scholar 

  • Fujinaka Y, Sakai T (2008) Mechanism design and the manipulation games of fair division. mimeo, Osaka University and Yokohama National University

  • Fujinaka Y, Wakayama T (2008) Secure implementation in economies with indivisible objects and money. Econ Lett 100: 91–95

    Article  Google Scholar 

  • Groves T (1973) Incentives in teams. Econometrica 41: 617–631

    Article  Google Scholar 

  • Holmström B (1979) Groves’ scheme on restricted domains. Econometrica 47: 1137–1144

    Article  Google Scholar 

  • Hurwicz L (1979) On the interaction between information and incentives in organization. In: Krippendorf K (eds) Communications and interactions in society. Scientific Publishers, New York, pp 123–147

    Google Scholar 

  • Littlechild SC, Owen G (1973) A simple expression for the shapley value in a special case. Manage Sci 20: 370–372

    Article  Google Scholar 

  • Ma J (1995) Stable matchings and rematching-proof equilibria in a two-sided matching market. J Econ Theory 66: 352–369

    Article  Google Scholar 

  • Maskin E (1999) Nash equilibrium and welfare optimality. Rev Econ Stud 66: 23–38

    Article  Google Scholar 

  • Miyagawa E (2001) House allocation with transfers. J Econ Theory 100: 329–355

    Article  Google Scholar 

  • Moulin H (1990) Fair division under joint ownership: recent results and open problems. Soc Choice Welf 7: 149–170

    Article  Google Scholar 

  • Moulin H (1992) An application of the shapley value to fair division with money. Econometrica 60: 1331–1349

    Article  Google Scholar 

  • Ohseto S (1999) Strategy-proof allocation mechanisms for economies with an indivisible good. Soc Choice Welf 16: 121–136

    Article  Google Scholar 

  • Ohseto S (2000) Strategy-proof and efficient allocation of an indivisible good on finitely restricted preference domains. Int J Game Theory 29: 365–374

    Article  Google Scholar 

  • Ohseto S (2004) Implementing egalitarian-equivalent allocation of indivisible goods on restricted domains. Econ Theory 23: 659–670

    Article  Google Scholar 

  • Ohseto S (2006) Characterizations of strategy-proof and fair mechanisms for allocating indivisible goods. Econ Theory 29: 111–121

    Article  Google Scholar 

  • Otani Y, Sicilian J (1982) Equilibrium and Walras preference games. J Econ Theory 27: 47–68

    Article  Google Scholar 

  • Otani Y, Sicilian J (1990) Limit properties of equilibrium allocations of Walrasian strategic games. J Econ Theory 51: 295–312

    Article  Google Scholar 

  • Postlewaite A, Wettstein D (1989) Feasible and continuous implementation. Rev Econ Stud 56: 603–611

    Article  Google Scholar 

  • Saijo T, Sjöström T, Yamato T (2007) Secure implementation. Theor Econ 2: 203–229

    Google Scholar 

  • Saijo T, Tatamitani Y, Yamato T (1996) Toward natural implementation. Int Econ Rev 37: 941–980

    Article  Google Scholar 

  • Sakai T (2005) Fair waste pricing: an axiomatic analysis to the NIMBY problem. mimeo, Yokohama National University

  • Sakai T (2007) Fairness and implementability in allocation of indivisible objects with monetary compensations. J Math Econ 43: 549–563

    Article  Google Scholar 

  • Schummer J (2000) Eliciting preferences to assign positions and compensation. Games Econ Behav 30: 293–318

    Article  Google Scholar 

  • Shapley LS (1953) A value for n-person games. In: Kuhn HW, Tucker AW (eds) Contributions to the theory of games, vol II. Ann Math Stud 28:307–317

  • Shin S, Suh S-C (1996) A mechanism implementing the stable rule in marriage problems. Econ Lett 51: 185–189

    Article  Google Scholar 

  • Sobel J (1981) Distortion of utilities and the bargaining problem. Econometrica 49: 597–619

    Article  Google Scholar 

  • Sönmez T (1997) Games of manipulation in marriage problems. Games Econ Behav 67: 677–689

    Google Scholar 

  • Sprumont Y (1991) The division problem with single-peaked preferences: a characterization of the uniform allocation rule. Econometrica 59: 509–519

    Article  Google Scholar 

  • Svensson LG (1983) Large indivisibles: an analysis with respect to price equilibrium and fairness. Econometrica 51: 939–954

    Article  Google Scholar 

  • Svensson L-G, Larsson B (2002) Strategy-proof and nonbossy allocation of indivisible goods and money. Econ Theory 20: 483–502

    Article  Google Scholar 

  • Tadenuma K, Thomson W (1993) The fair allocation of an indivisible good when monetary compensations are possible. Math Soc Sci 25: 117–132

    Article  Google Scholar 

  • Tadenuma K, Thomson W (1995a) Games of fair division. Games Econ Behav 9: 191–204

    Article  Google Scholar 

  • Tadenuma K, Thomson W (1995b) Refinements of the no-envy solution in economies with indivisible goods. Theory Decis 39: 186–206

    Google Scholar 

  • Takamiya K (2009) Preference revelation games and strong cores of allocation problems with indivisibilities. J Math Econ 45: 199–204

    Article  Google Scholar 

  • Tatamitani Y (1994) Coalition formation in games of fair division. Econ Lett 44: 371–376

    Article  Google Scholar 

  • Thomson W (1984) The manipulability of resource allocation mechanisms. Rev Econ Stud 51: 447–460

    Article  Google Scholar 

  • Thomson W (1987) The vulnerability to manipulative behavior of resource allocation mechanisms designed to select equitable and efficient outcomes. In: Groves T, Radner R, Reiter S (eds) Information, incentives, and economic mechanisms: essays in honor of leonid hurwicz. University of Minnesota Press, Minnesota, pp~375–396

  • Thomson W (1988) The manipulability of the Shapley value. Int J Game Theory 17: 101–127

    Article  Google Scholar 

  • Thomson W (2004) Manipulation of solutions to the problem of fair division when preferences are single-peaked. mimeo, University of Rochester

  • Thomson W (2008) Fair allocation rules In: Arrow K, Sen A, Suzumura K (eds) Handbook of social choice and welfare. North-Holland, Amsterdam (forthcoming)

  • Vickrey W (1961) Counterspeculation, auctions, and competitive sealed Tenders. J Finance 16: 8–37

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. JSPS Research Fellow/ISER, Osaka University, 6-1 Mihogaoka Ibaraki, Osaka, 567-0047, Japan

    Yuji Fujinaka

  2. Department of Economics, Yokohama National University, Yokohama, 240-8501, Japan

    Toyotaka Sakai

Authors
  1. Yuji Fujinaka
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Toyotaka Sakai
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Toyotaka Sakai.

Additional information

This paper was formerly circulated under the title “Allocations most realizable through strategic manipulation”. The authors are grateful to an anonymous referee, Shinji Ohseto, and Rakesh Vohra for their very detailed comments. They also thank seminar/conference participants at Kobe University, Osaka University, Kyoto University, University of Tokyo, the Spring 2006 meeting of Japanese Economic Association at Fukushima University, and the eighth international meeting of the Society for Social Choice and Welfare in Istanbul for helpful comments. Sakai acknowledges the financial support by KAKENHI (19310031).

Rights and permissions

Reprints and permissions

About this article

Cite this article

Fujinaka, Y., Sakai, T. The positive consequence of strategic manipulation in indivisible good allocation. Int J Game Theory 38, 325–348 (2009). https://doi.org/10.1007/s00182-009-0156-7

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00182-009-0156-7

Keywords

JEL Classification

Search

Navigation