Changes in the women’s labor market and education and their impacts on marriage and inequality: evidence from Brazil

Abstract

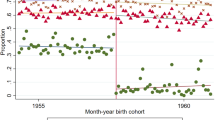
From 1992 to 2014, Brazil experienced a decline in income inequality along with a significant increase in schooling level, though the latter was more pronounced among women. Brazil also experienced a decline in returns to education, whereas an opposite trend was observed in several developed countries and China. In this paper, we evaluate the effects of educational, marital, and labor market factors on the income inequality of married couples. We also analyze how changes in educational assortative mating affect their income. Our findings suggest that changes in educational marital sorting parameters had a small but statistically significant effect on household income inequality. We show that growth in female labor force participation and a decrease in the gender wage gap explain part of the decline of the Gini coefficient. Educational factors also explain a part of that decline. Nevertheless, the main driver of the reduction in income inequality among couples appears to be the overall decrease in the returns to education.

Appendices

A Appendix

1.1 A.1 The steps to obtain the reweighting function $P_{x}^{\prime }(t_{e_{ij}}=b,t_{s}=t)$:

1) We draw one man from the husbands’ marginal distribution of education and one woman from the wives’ marginal distribution of education in $t=1992$. With probability

$$\begin{aligned} \Pr (Wife=i,t=1992).\Pr (Husband=j,t=1992), \end{aligned}$$

(19)

we obtain a man and a woman with educational levels i, j.

2) Considering the product of marginal distributions and the marital sorting parameter $s_{ij}(t)$, we decide whether the couple gets married. Hence, to construct the counterfactual we need to draw a man and woman from the marginal educational distributions of men and women and estimate $s_{ij}(t)$ . The probability of them getting married is

$$\begin{aligned} P^\prime =\Pr (Wife=i,t=b).\Pr (Husband=j,t=b).s_{ij}(t). \end{aligned}$$

3) If they get married, we draw³⁶ them from the marginal distributions of education and measure the probabilities in equation (19) again without that couple. We need to calculate the marginal distributions in every iteration. Then, we repeat the process until all couples have been formed.

B Appendix

1.1 B.1 standardized contingency table

To analyze whether positive assortative mating in Brazil increased from 1992 to 2014, we need to compare the joint distributions from these years. To this end, we standardize both joint distribution tables, considering the same marginal distributions. We use the Sinkhorn–Knopp algorithm that allows us to iterate over columns and rows, preserving the dependent relationship between the joint distribution and the marginal distributions.³⁷

1.2 B.2 Sinkhorn–Knopp Algorithm

We perform the following steps to execute the algorithm:

• 1- Divide the husbands’ marginal educational distribution as of 1992 (or 2014) by the marginal distribution as of the year used to standardize the table. We obtain a weight for each education level.

• 2- Divide the joint distributions in each row by these weights.

• 3- Divide the wives’ marginal educational distribution as of 1992 (or 2014) by the marginal distribution as of the year used to standardize the table. We obtain a weight for each education level.

• 4- Divide the joint distributions in each column by these weights.

• 5- Repeat steps 1-4 until the desired marginal distributions are obtained.

Tables 9 and 10 show the standardized table for 1992, obtained using the marginal distributions as of 2014 and the actual joint distribution as of 2014. In Table 9, we estimate the joint distribution as of 1992, using the marginal educational distributions as of 2014, and hold the dependence structure pattern of the joint distribution constant. We assess this analysis by calculating the odds ratio of the joint distribution as of 1992 (using the marginal educational distributions as of 2014) and the joint distribution as of 1992 in Table 15, and observe that it remains unchanged in both cases (Sinkhorn and Knopp (1967), Tan et al. (2004)).

C Appendix

In this section, we describe in more detail the variables used in the empirical exercises. We use household sampling weights to construct the variables.³⁸

1.1 C.1 family variables

1.1.1 C.1.1 Family ID

In Brazil, it is possible to have more than one family in the same household. To avoid counting two families as one, we create an identifier for each family. In the sample, we keep families constituted by couples of one man and one woman. Other family types (families with only one head of household or same-sex couples) are excluded from the sample. To construct the family ID, we use the following variables from the Brazilian National Household Sample Survey (PNAD): control number (v0102), serial number (v0103), the number associated with the household member (v0301), the number associated with the family (v0403), and status within the family (v0402 equal to 1 and 2).

1.1.2 C.1.2 Number of children

We add up the number of children in every family using the family ID, gender (v0302), age (v8005) between 0 and 17, and status within the family (v0402 equal to 3).

1.1.3 C.1.3 Age

We analyze spouses aged between 26 and 60. Single individuals, when included, are also between 26 and 60 years of age.

1.1.4 C.1.4 Levels of education

We construct a “years of schooling” variable to represent 0 to 17 years of schooling and aggregate values of this variable into five groups. In other words, individuals are grouped by the number of years of schooling into five mutually exclusive groups. The first group consists of illiterate (less than one year of education) individuals; the second contains those with elementary school education (4–5 years of schooling); the third comprises those with middle school (8–9 years of schooling) education; and the fourth group contains those who dropped out of and those who graduated from high school (10–12 years of schooling). The last group consists of individuals who had at least some postsecondary education regardless of whether they earned an undergraduate degree or M.A. or Ph.D. degrees (more than 12 years of schooling).

We use the following codes to form this variable: the code for school type and educational stage (v6003), grade attended (v0605), elementary school duration (v6030), highest educational stage attended (v6007), last grade completed of the educational stage attended previously (v0610), elementary school duration (v6070), and being able to read and write (v0601).

1.1.5 C.1.5 Couple’s income

This variable is the sum of individual monthly incomes of the husband and wife. We use the variable monthly income from all sources for individuals aged 10 or above (v4720).

1.2 C.2 Labor counterfactual variables

1.2.1 C.2.1 Female labor force participation

We develop the female labor force participation counterfactual using the reweighting function shown in equations (7) and (8) and described in Sect. 4.2.1. The reweighting function is the ratio of the proportion of working women in the base year and the actual year of interest for each of 25 combinations of male and female educational levels. Dummy variable w is 0 if variable v4704 is two; alternatively, w is 1 if v4704 is one.

1.2.2 C.2.2 Female wage gap

We develop the female wage gap counterfactual reweighting functions shown in equations (9) and (10) and following equations (7) and (8). They are described in Sects. 4.2.2 and 4.2.1, respectively.

In the first step, we calculate $\gamma$, which is the mean for each of 25 combinations of male and female educational levels, of men’s and women’s incomes (v4720). Next, for every woman, we calculate $\vartheta$, which is the product of $\gamma$ and the income of the woman’s husband.

We then create a dummy variable $\omega$, which takes the value of 1 if the wife’s income is greater than $\vartheta$ and is zero otherwise.

The reweighting function is the ratio of the proportion of women with $\omega$ equal to one (or equal to zero) and the total number of women, in the base year and the actual year of interest for each of 25 combinations of male and female educational levels.

1.3 C.3 Marriage counterfactual variables

1.3.1 C.3.1 Marital sorting parameter

To construct the reweighting function, we follow equation (15) and steps (1) to (3) described in Sect. 4.2.3, setting $t_{ij}=t$ and $t_{s}=b$. The methodology for $s_{ij}$ is described in Sect. 4.1.

1.3.2 C.3.2 Random matching

To construct the reweighting function, we follow equation (15), setting $t_{ij}$=t, and steps (1) to (3) described in Sect. 4.2.3. In this case, we set $s_{ij}=1$.³⁹

1.4 C.4 Educational counterfactual variables

1.4.1 C.4.1 Educational composition

To construct the reweighting function, we follow equation (15) and steps (1) to (3) described in Sect. 4.2.3.

1.4.2 C.4.2 Returns to education

We use the income distribution in year b. The reweighting function being calculated is the ratio of the joint distribution of the couples’ education in year t and year b for all education levels. We then calculate the income distribution using this reweighting function to evaluate the impact of returns to education on the distribution.