1 Motivation

Quantifying the uncertainty around economic forecasts has recently received much attention (e.g., Jurado et al. 2015; Müller and Watson 2016). The most general information on uncertainty is provided by forecast distributions, such as the ‘fan charts’ of inflation issued by the Bank of England. A key benefit of forecast distributions is that each forecast user—such as a pension fund manager or a private consumer—can extract the specific piece of information that is relevant to them.

Fig. 1
figure 1

Left panel Forecast distributions for the GDP growth rate in 2013:Q3, made in February 2013. Right panel Forecast distributions for the inflation rate of the harmonized index of consumer prices (HICP) in December 2013, made in February 2013. Both panels Gray bars represent ECB-SPF histogram forecasts; small vertical green lines at bottom are ECB-SPF point forecasts; vertical black lines are realizing observations

Full size image

The present paper seeks to construct forecast distributions from the European Central Bank’s Survey of Professional Forecasters (SPF). The data contain point forecasts made by several participants, and we consider so-called ensemble methods (e.g., Raftery et al. 2005) for converting these into a forecast distribution. Furthermore, SPF participants assess the probability that the predictand falls into one of several prespecified ranges (below zero, between 0 and 0.5%, between 0.5 and 1%, etc). Taken together, these assessments imply a histogram-type forecast distribution.

Comparing ensemble versus histogram methods is relevant for several reasons: First, in a situation where both methods are available, the comparison provides guidance for choosing one of them. Second, given that histogram-type forecasts are unavailable in many data sets, there is a question of whether ensembles are a satisfactory alternative. Third, the results of the comparison might inform the design of future expert surveys, provided that the focus lies on forecast performance. Krüger and Nolte (2016, Section 6) have recently compared ensembles versus histograms for the US SPF data. The present study conducts a similar, but more detailed, comparison for the ECB-SPF data. The ECB-SPF data are ideally suited for that purpose, since it covers point forecasts and histograms for exactly the same target variable. By contrast, the formats of point and probabilistic forecasts are not aligned in the US SPF, such that comparisons require approximations or are restricted to a subset of time periods. Other popular economic surveys, such as the commercial Blue Chip and Consensus data, do not cover probabilistic forecasts.

Fig. 2
figure 2

Prediction intervals and realizations, plotted over time. Blue areas correspond to BMA prediction intervals (ranging from the 15th to 85th percentile of the forecast distribution); orange areas correspond to histogram prediction intervals. Both panels refer to 1-year-ahead forecasts

Full size image

Figure 1 illustrates our analysis for the 2013:Q2 edition of the ECB-SPF survey: While the gray bars represent histogram probabilities (on average over participants), the blue curve is the forecast distribution implied by an ensemble method (BMA) that derives from the point forecasts, and the orange curve is a continuous distribution fitted to the histogram. We emphasize that the forecast distributions are out-of-sample, that is, they are constructed from data that would have been available in real time. Figure 1 shows that for both GDP growth and inflation, the ensemble distribution is much more dispersed than the histogram. As detailed below, this effect arises because the ensemble method incorporates information on past forecast errors, which were large around the great recession. The ensemble variance is an objective measure of forecast uncertainty. This objective measure clearly exceeds survey participants’ subjective uncertainty as expressed by the histogram distribution. This relationship extends beyond the 2013:Q2 example. Figure 2 visualizes the 70% central prediction intervals of both methods over time: The BMA prediction intervals are wider than those of the histogram, particularly toward the end of the sample, in the wake of the great recession. The latter caused sharp downward spikes in GDP growth and inflation, as well as large absolute errors of the methods’ point forecasts. As a consequence, the spread of the ensemble methods’ prediction intervals increases markedly. By contrast, the spread of the histogram prediction intervals increases only marginally after the crisis (see Sect. 4.3).

Our analysis relates to a number of recent empirical studies on the ECB-SPF data (e.g., Genre et al. 2013; Kenny et al. 2014, 2015; Abel et al. 2016; Glas and Hartmann 2016). Compared to these studies, the main innovation of the present paper is our use of ensemble methods for constructing forecast distributions. Ensemble methods are used extensively in meteorology (e.g., Gneiting and Raftery 2005); they have received little attention in economics, with the exception of Gneiting and Thorarinsdottir (2010) and Krüger and Nolte (2016) who analyze US SPF data. Furthermore, ensemble methods may account for disagreement in the point forecasts of individual participants.Footnote 1 Starting with Zarnowitz and Lambros (1987), several economic studies have analyzed the relation between disagreement and various notions of forecast uncertainty. As an important contribution to this literature, Lahiri and Sheng (2010) present a factor model which bridges the gap to structural models of expectation formation (e.g., Lahiri and Sheng 2008). By contrast, our results constitute reduced form evidence on the role of forecast disagreement in the ECB-SPF data. Finally, our approach of constructing out-of-sample forecast distributions is different from estimating a historical trajectory of economic uncertainty given all data available today. This conceptual difference explains why the prediction intervals in our Fig. 2 do not cover the large downward spikes of the great recession, whereas uncertainty measures such as the ones reported in Jurado et al. (2015, Figures 1 to 4) tend to peak during recessions.Footnote 2

The rest of this paper is organized as follows. Section 2 describes the data, highlighting stylized facts that are important for the design of forecasting methods. Section 3 presents the formal framework of our analysis, detailing methods for evaluating and constructing forecasts. Section 4 presents the empirical results, and Sect. 5 concludes.

2 Data on forecasts and realizations

Survey forecasts from the ECB-SPF are available quarterly, starting in 1999:Q1 (see European Central Bank 2016a). We consider forecasts of GDP growth and HICP inflation in the Euro Area; the horizon is one and two years ahead, relative to the most recent available observation. For example, when the 2006:Q4 round of the survey was conducted, the latest available observation on GDP was for 2006:Q2. Hence, the one and two-year-ahead forecasts refer to 2007:Q2 and 2008:Q2, respectively.

For the variables and sample period we consider, the number of participants per survey round ranges from 32 to 64, with a median of 47. However, the composition of this group varies heavily over time. As an example, consider one-year-ahead point forecasts of GDP growth. There are 101 distinct participants who submitted a forecast in at least one of the survey rounds. However, in a typical survey round, only about half of these participants are available. This missing data issue creates a major challenge for forecast combination in the ECB-SPF data. See Genre et al. (2013) for further details, and Capistrán and Timmermann (2009) on missingness in the US SPF data, for which the situation is similar. These data properties motivate a number of simple yet principled combination methods which we describe in Sect. 3.2.

Figure 3 shows time series plots of the two predictands, based on real-time data available from the ECB’s statistical data warehouse (European Central Bank 2016b). The relevant series codes are RTD.Q.S0.S.G_GDPM_TO_C.E and RTD.M.S0.N.P_C_OV.A. GDP is measured at quarterly frequency, whereas HICP inflation is monthly. For both series, updated data vintages are released about once per month.

Fig. 3
figure 3

Time series plots of the GDP growth rate (left) and the growth rate of the HICP (right). Both series are year-over-year growth rates. In both panels, the June 2015 vintage of the data is printed in black, and earlier vintages are printed in grayscale

Full size image

In our empirical analysis, we adopt a real-time perspective in order to roughly match the information set of SPF participants: When fitting a statistical forecast for a given quarter, we use historical data that would have been available on the first day of the quarter’s second month (e.g., February 1, 2013 for 2013:Q1). While the exact schedule of the ECB-SPF survey varies slightly over time (see the documentation by European Central Bank 2016a), our procedure provides a simple approximation that seems reasonably accurate. Finally, we compare all forecasts against the ’final’ (June 2015) vintage of the data.

3 Forecasting methods

This section describes how we evaluate forecasts, and introduces the forecasting methods we consider.

3.1 Measure of forecast accuracy

We measure the accuracy of distribution forecasts via the Continuous Ranked Probability Score (CRPS; Matheson and Winkler 1976; Gneiting and Raftery 2007). For a cumulative distribution function F (i.e., the forecast distribution) and a realization \(y \in \mathbb {R}\), the CRPS is given by

$$\begin{aligned} \text {CRPS}(F, y) = \int _{-\infty }^{\infty } (F(z) - 1(z \ge y))^2~\mathrm{d}z, \end{aligned}$$
(1)

where 1(A) is the indicator function of the event A. Closed-form expressions of the integral in (1) are available for several types of distributions F, such as the two types we use below: the two-piece normal distribution (Gneiting and Thorarinsdottir 2010) and mixtures of normal distributions (Grimit et al. 2006). Our implementation is based on the R package scoringRules (Jordan et al. 2016) which includes both of these variants.

3.2 Ensemble-based methods

Let \(x_{t+h}^i\) denote the point forecast of participant i, made at date t for date \(t + h\). Furthermore, let \(\mathcal {S}_{t+h}\) denote the collection of available participants, and denote by \(N_{t+h} = |\mathcal {S}_{t+h}|\) the number of participants. As described above, the set of available participants may change over time and across forecast horizons. Ensemble methods construct a forecast distribution for \(Y_{t+h}\), based on the individual forecasts \(\{x_{t+h}^i\}_{i\in \mathcal {S}_{t+h}}\). The ensemble forecast may depend on ‘who says what’, that is, it may vary across permutations of the indexes \(i \in \mathcal {S}_{t+h}\). If that is the case, the individual forecasters are said to be non-exchangeable. Alternatively, if the ensemble forecast is invariant to ‘who says what’, the forecasters are said to be exchangeable.

In order to treat forecasters as non-exchangeable, one must be able to compare them. For example, if we knew that Anne is a better forecaster than Bob, we might want to design an ensemble method which puts more weight on Anne’s forecast than on Bob’s. However, relative performance is hard to estimate in the ECB-SPF data set, since the past track records of different forecasters typically refer to different time periods. Similarly, estimating correlation structures among the forecasts, as is required for regression-type combination approaches (e.g., Timmermann 2006), requires to impute the missing forecasts in some way. Given the difficulties just described, it is perhaps not surprising that Genre et al. (2013) find very little evidence in favor of either performance-based or regression methods for the ECB-SPF data. Motivated by these concerns, we consider two simple ensemble methods which treat the forecasters as exchangeable:

  1. 1.

    The first method (‘BMA’) constructs a forecast distribution as follows:

    $$\begin{aligned} f_{t+h}^\text {BMA} = \frac{1}{N_{t+h}} \sum _{i \in \mathcal {S}_{t+h}} \mathcal {N}(x_{t+h}^i, \theta ), \end{aligned}$$
    (2)

    where \(\theta \in \mathbb {R}_+\) is a scalar parameter to be estimated. In words, (2) posits an equally weighted mixture of \(N_{t+h}\) forecast distributions, each of which corresponds to an individual forecaster i. Each of these distributions is assumed to have the same variance, \(\theta \). The method has been proposed by Krüger and Nolte (2016), who find that it performs well for the US SPF data. The label ‘BMA’ hints at the method’s close conceptual connection to the Bayesian model averaging approach proposed by Raftery et al. (2005) in the meteorological forecasting literature. Denote the mean of the survey forecasts by \(\bar{x}_{t+h} = N_{t+h}^{-1} \sum _{i \in \mathcal {S}_{t+h}} x_{t+h}^i\). Then, the variance of the forecast distribution in (2) is given by \(D_{t+h} + \theta \), where

    $$D_{t+h} = N_{t+h}^{-1} \sum _{i \in \mathcal {S}_{t+h}} \left( x_{t+h}^i-\bar{x}_{t+h}\right) ^2$$

    is the cross-sectional variance of the survey forecasts (‘disagreement’). The two-component structure of the BMA forecast variance is similar to the model by Ozturk and Sheng (2016) which decomposes forecast uncertainty into a common component (similar to \(\theta \) in Eq. 2) and an idiosyncratic component (which they proxy by forecaster disagreement, \(D_t\)).

  2. 2.

    The ‘EMOS’ method assumes that

    $$\begin{aligned} f_{t+h}^\text {EMOS} = \mathcal {N}(\bar{x}_{t+h}, \gamma ), \end{aligned}$$
    (3)

    where \(\gamma \in \mathbb {R}_+\) is a parameter to be estimated. The method simply fits a normal distribution around the mean of the survey forecasts. Unlike in the BMA method, forecaster disagreement does not enter the variance of the distribution. The label ‘EMOS’ alludes to the method’s similarity to the ensemble model output statistics approach of Gneiting et al. (2005), again proposed in a meteorological context.

Both ensemble methods require only one parameter to be estimated, which can be done via grid search methods. In each case, we fit the parameter to minimize the sample average of the CRPS (see Sect. 3.1), based on a rolling window of 20 observations. Conceptually, the BMA method is based on the idea of fitting a simplistic distribution to each individual forecaster, and then averaging over these distributions. This is why Krüger and Nolte (2016) call it a ‘micro-level’ method. In contrast, the EMOS method fixes a normal distribution and fits the parameters of that distribution via a summary statistic (the mean) from the ensemble of forecasters.

3.3 Survey histograms

In our out-of-sample analysis, we consider the average histogram over all forecasters (for a given date, variable, and forecast horizon). In order to convert the histogram into a complete forecast distribution, we consider a parametric approximation, obtained by fitting a two-piece normal distribution (Wallis 2004, Box A) to the histogram. Specifically, the parameters of the approximating distribution solve the following minimization problem (suppressing time and forecast horizon for ease of notation):

$$\begin{aligned} \min _{\mu , \sigma _1, \sigma _2} \sum _{j=1}^J \left[ P_j - F_{\text {2PN}}(r_j; \mu , \sigma _1, \sigma _2)\right] ^2, \end{aligned}$$
(4)

where \(r_j\) is the right endpoint of histogram bin \(j = 1, \ldots , J\); \(P_j\) is the cumulative probability of bins 1 to j, and \(F_{\text {2PN}}(\cdot ~; \mu , \sigma _1, \sigma _2)\) is the cumulative distribution function of the two-piece normal distribution with parameters \(\mu , \sigma _1\) and \(\sigma _2\).

Parametric approximations to survey histogram forecasts have been proposed by Engelberg et al. (2009), who consider a very flexible generalized beta distribution as an approximation. In our case, replacing the two-piece normal distribution by a conventional Gaussian distribution yielded very similar forecasting results, suggesting that the flexibility of the two-piece normal is well sufficient.

3.4 Simple time series benchmark model

We also compare the ECB-SPF to a simple Gaussian benchmark forecast distribution, with mean equal to the random walk prediction, and variance estimated from a rolling window of 20 observations (in line with the sample used for fitting the ensemble methods). Specifically, denote the series of training sample observations by \(\{y_t\}_{t = T-19}^T.\) Then, the benchmark distribution has mean \(y_T\) and variance \(h_q \times \frac{1}{19} \sum _{t = T-18}^T (y_t-y_{t-1})^2,\) where \(h_q\) is the forecast horizon (in quarters). Our choice of the random walk is motivated by the quarter-on-quarter definition of the predictands, which implies considerable persistence almost by definition (see Fig. 3).Footnote 3

4 Empirical results

This section summarizes parameter estimates of interest, presents the main results of our out-of-sample analysis, and then provides some further analysis of forecast uncertainty in ensembles and histograms.

4.1 Parameter estimates for ensembles

As described in Sect. 3.2, the two ensemble methods entail different assumptions on the role of forecaster disagreement; Table 1 summarizes the parameter estimates of both methods. Recall that the forecast variance of BMA is given by the sum of \(\theta \) and the cross-sectional variance of point forecasts (disagreement); the forecast variance of EMOS is given by \(\gamma \). As shown in Table 1, the estimates of \(\theta \) are only marginally smaller than the estimates of \(\gamma \). This implies that disagreement plays a very limited role in predicting forecast uncertainty for the ECB-SPF data. Also, note that the ensemble parameters for inflation are slightly smaller for two-year-ahead forecasts than for one-year-ahead forecasts, which points to possible model misspecification (c.f. Patton and Timmermann 2012).

Table 1 Parameter estimates for the ensemble methods introduced in Sect. 3.1 (median over rolling windows)
Full size table

4.2 Forecast performance

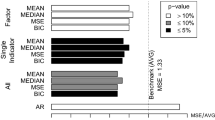
Table 2 contains our main empirical results. In addition to the average CRPS values, the table indicates the results of Diebold and Mariano (1995) type tests for the null hypothesis of equal predictive ability compared to the BMA method. We construct the test statistic as described in Krüger et al. (2015, Section 5). The results can be summarized as follows.

  • The ensemble-based methods (BMA and EMOS) perform very similarly for both variables and forecast horizons. This is striking, given that the two specifications feature quite different variance specifications. Together with the parameter estimates reported in Table 1, the result suggests that forecaster disagreement does not have a systematic impact on forecast performance.

  • The accuracy of the survey histograms is comparable to the ensemble-based methods. While the histograms attain slightly worse CRPS scores for both variables and forecast horizons, these differences are not statistically significant at the 5% level.

  • The random walk time series benchmark attains worse CRPS scores than the (ensemble or histogram based) survey methods in all instances. The difference to BMA is statistically significant at the 10% level for GDP, but not for inflation.

Our finding that disagreement is of limited help for distribution forecasting differs from the results by Krüger and Nolte (2016), who find that disagreement in US SPF forecasts does have predictive power for some variables and forecast horizons. A possible explanation for this discrepancy is that Krüger and Nolte (2016) consider a longer sampling period, with more variation of disagreement over time. This may help to identify effects which are hard to identify in our short sample. This interpretation is also supported by the results of Boero et al. (2015). They consider data from the Bank of England’s Survey of External Forecasters (SEF) for the 2006–2012 sample period and find no close relation between disagreement and squared forecast errors. They conclude that “[..] the joint results from the US [SPF] and UK [SEF] surveys suggest the encompassing conclusion that disagreement is a useful proxy for uncertainty when it exhibits large fluctuations, but low-level high-frequency variations are not sufficiently correlated.” (Boero et al. 2015, p. 1044). Our results for the ECB-SPF data are in line with this view. Furthermore, the forecast horizons we consider are fairly long by macroeconomic standards. The limited role of disagreement at long horizons is in line with the factor model by Lahiri and Sheng (2010).

Table 2 Continuous Ranked Probability Score (CRPS), averaged over the evaluation period (2005:Q3 to 2015:Q1 for 1-year-ahead forecasts; 2007:Q3 to 2015:Q1 for 2-year-ahead forecasts)
Full size table
Fig. 4
figure 4

Length of 70% prediction intervals, for individual and average histograms (approximated via two-piece normal distributions), and for the BMA ensemble method. Forecasts are 1 year ahead

Full size image

4.3 Forecast uncertainty in ensembles and histograms

As seen from Table 2, the performance of ensemble and histogram methods is not statistically different. However, their similar performance does not necessarily mean that the methods produce similar forecast distributions. Indeed, as suggested already by Fig. 2, the methods tend to differ substantially in practice.

Comparing the prediction intervals in Fig. 2 to the realizing values (black line), it turns out that the BMA intervals cover the realization in 68% of all cases for GDP, and in 62% of all cases for inflation. These numbers are reasonably close to the desired nominal coverage level of 70%. By contrast, the histogram prediction intervals cover the realizations in only 38% of all cases (for both GDP and inflation), implying that the histogram-based forecast distributions are overconfident.Footnote 4

In principle, our result that the average survey histogram is overconfident may conceal important differences in individual-level uncertainty, which are studied by Lahiri and Liu (2006, US SPF data), Boero et al. (2015, UK SEF data), and others. To investigate this possibility, Fig. 4 plots the length of the individual participants’ prediction intervals over time. These numbers are computed by fitting a two-piece normal distribution to each individual histogram, as described in Sect. 3.3, and then computing the lengths of the prediction intervals for the resulting two-piece normal distributions.Footnote 5 For most quarters between 2010 and 2014, all individual forecast histograms yield shorter prediction intervals than the BMA ensemble, indicating that our result is not driven by a few individuals. Finally, the findings from Fig. 4 are in line with Kenny et al. (2015) who analyze the determinants of individual-level forecast performance in the ECB-SPF. They find that ”[..] many experts [..] are underestimating uncertainty and could improve their density performance by simply increasing their variances.” (Kenny et al. 2015, p. 1229)

5 Conclusion

The key result of this paper is that point forecasts are useful for constructing forecast distributions, by means of ensemble methods. Motivated by earlier results for the ECB-SPF (Genre et al. 2013), we focus on very simple variants of these methods, based on a single parameter to be estimated. We find that these methods perform well relative to survey histograms also contained in the ECB-SPF. This suggests that ensemble methods are promising for other survey data sets, which typically comprise point forecasts only.

We further find that ensembles—which estimate the statistical uncertainty from past forecast errors—consistently generate wider prediction intervals than subjective survey histograms (see Figs. 2, 4). This gap between objective versus subjective uncertainty calls for further analysis as the time series dimension of the ECB-SPF data grows larger. Kajal Lahiri’s research on uncertainty, heterogeneity and learning in macroeconomic expert surveys offers important methodological and empirical insights to guide such an analysis.