Abstract
We use multi-unit multi-bid common value auction models with private information to draw empirical implications on how bidding behavior in bond auctions is affected by secondary market price volatility, implications that we test using individual bidding data for 88 bond auctions held between 2003 and 2007 by the Spanish Treasury. The main novelty of the paper is that we analyze the effect of volatility in bidders heterogeneous behavior within an auction. We provide evidence that, as the theoretical models predict, the heterogeneity of bidders’ bid shading increases with volatility and that, on average across auctions, bid shading and bidders’ profit also increase with volatility.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
Notes
We use their examples for their more general models, presented in Sect. 4.2 for AM and Sect. 4.4 for WZ.
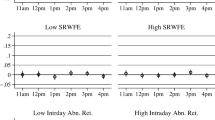
Bid spread is the difference between the highest and the lowest bid. Bid shading or discount is the difference between the expected value of the good at the time of bidding and the average bid price.
The winner’s curse or champion’s plague in multi-unit auctions, arise in common value models with private information, since the bidder’s conditional expected value is decreasing in the number of units that he wins. Hence bidders shade their bids to adjust ex ante. This expression is from Gordy (1999).
See Hortaçsu (2011) for a survey on structural models.
The maximum number of bids in a demand is 11 bids.
The first tier or blind market is the core of the public debt market, reserved for market members or account holders; trades are conducted without the knowledge of the counter party identity and transaction size is a minimum of 5 million Euros.
Except for 2006.
It includes the date and time of the trade, the market on which the trade occurs, ISIN code, if the dealer is buying or selling, the price and the size of the trade, whether the originating order was completely filled or only partially filled, and the profile of the aggressor member on that market.
http://www.bde.es/webbde/es/secciones/informes/banota/series.html, files CONTYYYY.TXT.
See Appendix 1 for additional details on the volatility estimation.
Fills from MTS. We also used the price of the transaction closest to the auction time, on the interval [\(-\)10 min, +10 min] around the auction time. We had data on that interval for 50 of the 88 bond auctions on the data, and the average discount is not significantly different from 0.
For discriminatory auctions, Rocholl (2006) reports for Germany a discount that increases with duration, ranging from 0.076 to 0.149, while Nyborg et al. (2002) report for Swedish bonds with duration between 5- and 8-year discounts that range from 0.252 to 0.478. For uniform auctions, Keloharju et al. (2005) reports for Finnish Treasury bond auctions a positive and significant discount of 0.081. The negativity of discount could be explained either by overbidding or by the V-effect. There is overbidding when bidders bid above the market price at the time of the auction, a problem of the primary dealer structure, as documented by Dunne et al. (2010). The V-effect, documented by Pacini (2006) for Treasury auctions in Italy and France, consist on secondary market prices on the auction date that move with a V-shape, with the V lower corner at the auction time.
To adjust to the settlement date, we first calculate the internal rate of return for the bond, and then, we use it to obtain the price as the sum of the present value of the expected cash flow (where the cash flow is the annual coupon plus the maturity value). We also calculated profit with the same price that we use when calculating discount, the price of the transaction closest to the auction time on the interval [\(-\)10 min, +10 min]. However, we have data only for 50 bond in that interval, and additionally, average profit are negative, on average, and significantly different from zero. As we argued on Footnote 14, Market Makers may lower their bid and ask quotes around the time of the auction, so we consider that transactions on the day after the auction are a more reliable measure of profit.
Maximum profit because although Treasury auctions in Germany are discriminatory, he reports the difference between the market price of the security and the auction clearing price, lower than the quantity weighted price of winning bids.
Armantier and Sbaï (2006) rely on numerical techniques to approximate the Bayesian Nash equilibrium in a common value model with private information and then estimate the structural parameters of the model; their approach is beyond the scope of this paper.
Sect. 4.2 for AM and Sect. 4.4 for WZ.
Without loss of generality, \(p_h({s}_i)\ge p_l({s}_i)\) for all \({s}_i\), so that \(p_h({s}_i)\) and \(p_l({s}_i)\) denote the high and low bid, respectively.
With respect to the discriminatory auction, in Alvarez and Mazón (2007) we find that bid spread is larger for the Spanish than for the discriminator auction, both because the high bid is greater and the low bid is lower in the Spanish than in the discriminatory auction. We find the equilibria numerically, and there are parameter values for which equilibria do not exist or for which there are multiple equilibria, which limits the predictive capacity of the model. In contrast, in AM there is a unique equilibrium given the assumptions of the model.
In the model, given a value for \(\sigma ^2_v\), the value for \(\sigma ^2_{\varepsilon }\) is such that \(\frac{\sigma ^2_{v}}{\sigma ^2_{\varepsilon }}\) is an integer \(>\)1.
Remember that \(\frac{\sigma ^2_{v}}{\sigma ^2_{\varepsilon }}\) is an integer \(>\)1.
Results do not vary when we consider risk averse bidders, taking positive values for \(\rho \).
We vary \(\sigma _{\varepsilon }^2\) in order to check the robustness of the analysis to a parameter whose value is not directly related to the data.
Fig. 2 
Bidding behavior and volatility for the AM and WZ’s uniform auction, a \(AM^u\) Avg Bid Spread, b \(AM^u\) Avg High Bid, c \(AM^u\) Avg Low Bid, d \(AM^u\) Std Bid Spread, e \(AM^u\) Std High Bid, f \(AM^u\) Std Low Bid, g WZ Avg Bid Spread, h WZ Avg Discount, i WZ Std Bid Spread, j WZ Std Discount
It can be shown analytically that the weighted average price is one-third of the demand intercept.
Note that for the WZ’s model, there is a family of parallel demands for different signal observations, which shifts clockwise as volatility increases. Additionally, since there is a mean preserving spread on the distribution of the value of the good and therefore on the distribution of signals as volatility increases, the range of possible demand intercepts increases with volatility.
With a p value equal to 0.1 for Dummy B30.
We do not report regressions of the mean and standard deviation of the number of bids per bidder in an auction; neither of them is significantly correlated with volatility.
Table 9 Bidding behavior, auction results and volatility IV (standard deviations) Although the model implies correctly that the standard deviation of discount and volatility are positively correlated for low values of volatility.
The duration of a financial asset that consists of fixed cash flows, as a bond, is the weighted average of the times until those fixed cash flows are received, with the weights proportional to the present value of the payment. It is a measurement of how long, in years, it takes for the price of a bond to be repaid by its internal cash flows. Duration is defined as
$$\begin{aligned} D = \frac{1}{P} \sum _{t=1}^T t \frac{CF_t}{(1+r)^t} \end{aligned}$$where T is the number of cash flows, \(CF_t\) is the cash flow at time t, t is the time in years until the payment will be received, r is the internal rate of return, and P is the bond price. The internal rate of return, r, is the rate that makes the net present value of all cash flows equal to zero. In other words, it is the rate at which an investment breaks even.
The Treasury also issues Letras del Tesoro, Treasury bills, short-term instruments, with 3, 6, 12 and 18 months maturity. In this paper we do not analyze Treasury bill auctions, since the secondary market for bills is very illiquid and there is not a reliable measure of secondary market volatility.
References
Alvarez F, Mazón C (2007) Comparing the Spanish and the discriminatory auction formats: A discrete model with private information. European J Oper Res 179(1):253 – 266, doi:10.1016/j.ejor.2006.02.044, http://www.sciencedirect.com/science/article/pii/S0377221706002505
Alvarez F, Mazón C (2012) Multi-unit auctions with private information: an indivisible unit continuous price model. Econ Theory 51(1):35–70. doi:10.1007/s00199-010-0594-2
Armantier O, Lafhel N (2009) Comparison of auction formats in Canadian government auctions. Tech. rep., Bank of Canada Working Paper
Armantier O, Sbaï E (2006) Estimation and comparison of treasury auction formats when bidders are asymmetric. J Appl Econ 21(6):745–779. doi:10.1002/jae.875
Arnone M, Iden G (2003) Primary Dealers in Government Securities: policy Issues and Selected Countries Experience (EPub). International Monetary Fund
Cammack EB (1991) Evidence on bidding strategies and the information in treasury bill auctions. J Politic Econ 99:100–130
Dunne PG, Moore M, Portes R (2010) European government bond markets: Transparency, liquidity, efficiency. Tech. rep., CEPR Research Report
Elsinger H, Zulehner C (2007) Bidding behavior in austrian treasury bond auctions. Monet Policy Econ Q 2:109–125
Fevrier PRP, Visser M (2002) Econometrics of share auctions. Working Papers 2002-09, Centre de Recherche en Economie et Statistique, http://ideas.repec.org/p/crs/wpaper/2002-09.html
Goldreich D (2007) Underpricing in discriminatory and uniform-price treasury auctions. J Financ Quant Anal 42:443–466, doi:10.1017/S0022109000003343, http://journals.cambridge.org/article_S0022109000003343
Gordy MB (1999) Hedging winner’s curse with multiple bids: evidence from the Portuguese treasury bill auction. Rev Econ Stat 81:448–465
Hortaçsu A (2002) Bidding behavior in divisible good auctions: Theory and empirical evidence from Turkish treasury auctions, working paper
Hortaçsu A (2011) Recent progress in the empirical analysis of multi-unit auctions. Int J Ind Organ 29(3):345–349
Hortaçsu A, McAdams D (2010) Mechanism choice and strategic bidding in divisible good auctions: an empirical analysis of the Turkish treasury auction market. J Political Econ 118(5):833–865
Kang BS, Puller SL (2008) The effect of auction format on efficiency and revenue in divisible goods auctions: a test using Korean treasury auctions. J Ind Econ 56(2):290–332. doi:10.1111/j.1467-6451.2008.00342.x
Kastl J (2011) Discrete bids and empirical inference in divisible good auctions. Rev Econ Stud 78(3):974–1014
Keloharju M, Nyborg KG, Rydqvist K (2005) Strategic behavior and underpricing in uniform price auctions: Evidence from Finnish treasury auctions. J Financ 60(4):1865–1902, http://ideas.repec.org/a/bla/jfinan/v60y2005i4p1865-1902.html
Nyborg KG, Rydqvist K, Sundaresan SM (2002) Bidder behavior in multiunit auctions: evidence from Swedish treasury auctions. J Political Econ 110(2):394–424
Pacini R (2006) Auctioning government securities: the puzzle of overpricing. Economics 1:1–45
Rocholl J (2006) Discriminatory auctions with seller discretion: evidence from German treasury auctions. Tech. Rep. 15/2005, Deutsche Bundesbank, Kenan-Flagler Business School, University of North Carolina at Chapel Hill
Wang JJ, Zender JF (2002) Auctioning divisible goods. Econ Theory 19(4):673–705. doi:10.1007/s001990100191
Wilson R (1979) Auctions of shares. Q J Econ 93:675–689
Acknowledgments
We thank Soledad Nuñez and Enrique Martín Quilis from Secretaría General del Tesoro for providing the auction data and for insightful conversations, Antonio Díaz for helping us with financial questions, Barry Readman for the linguistic revision of the text and specially two anonymous referees for many valuable comments and suggestions. Any remaining error is our responsibility. We thank the financial support from Ministerio de Educación y Ciencia, grant SEJ2007-65722.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Institutional background—additional details
1.1 Auctions
The Spanish Treasury issues Bonos y Obligaciones del Estado, Treasury bonds, securities with maturities above 2 years, paying annual coupons. Maturities for Bonos are 3 and 5 years, while Obligaciones have maturities of 10, 15 and 30 years.Footnote 31 Bids must be made for at least 1000 Euros or a multiple of this minimum amount, and are either competitive, specifying both the quantity desired and the price, or non-competitive, specifying only the quantity desired. Non-competitive bids are accepted in full and pay the auction’s weighted average price. There is a maximum of 1,000,000 Euros on non-competitive bids submitted by each participant. Any investor can submit bids in the auctions, although most bids are made by Market Makers, a group of financial institutions with given obligations and rights, whose purpose is to stimulate the liquidity of the secondary market in public debt and cooperate in the diffusion of government debt domestically and abroad. To qualify as a Market Maker, institutions must apply to the Treasury and fulfill some requirements that include presenting at each auction requests for a minimal nominal value of 3 percent of the amount sold by the Treasury for each type of instrument, at prices not less than the stop-out price, less a given amount, that depends on the maturity. Additionally, they have to guarantee the liquidity of the secondary market, with listing obligations. As a compensation, they may present requests on the day of the auction until the time of the auction. They also have exclusive access to the second rounds, carried out between the resolution of the auction and the 12 h of the working day before the issue is put into circulation, and the top ranked are chosen to carry out debt management deals.
Over the period considered, the mean aggregate quantity demanded is 2747 thousand millions of Euros, while the mean auction size is 1334 thousand millions of Euros, with a mean cover ratio of 2.15.
1.2 Secondary markets
Secondary market trades for Spanish government debt are conducted through three systems, two of them, the first and second tier, reserved for market members or account holders, and the third for transactions between market members and third parties. The first tier or blind market is an electronic platform in which trades are electronically conducted without the knowledge of the counter party identity. This is the core of the public debt market, as participating agents undertake to quote bid and ask prices at relatively narrow spreads (around 5 basis points in keenly traded issues), thereby guaranteeing the market’s overall liquidity. Transaction size is a minimum of 5 million Euros. Blind market trades may only be to maturity, whether in spot or forward transactions.
Appendix 2: Volatility estimations—additional details
The estimated ARCH(1) model is
When there are no data for a bond in a given day, first we use a time series interpolation within a five-day window, i.e., if there are data for that bond around the missing date, and no more than 5 days have elapsed, we use for the missing day the average of the two closest dates. If there are no data in that window, we use the price of the traded Treasury bond with duration that most closely mimics the duration of the new Treasury bond for the day in which the data are missing. When a new Treasury bond is auctioned, we use the average winning auction yield to compute duration.
Table 11 presents estimates for the model for each ISIN code.
Panel (a) in Fig. 5 shows the histogram for the values of volatility for all 10-year bonds in our sample. Panel (b) show the histogram for the values of volatility on auction days, the subsample that we use on the empirical regressions. Finally, panel (c) plots an example for a specific bond; the vertical lines are auction days for that particular bond.
Table 12 presents rank correlation tests between cont and best volatility time series. The null hypothesis (no correlation) is rejected against the alternative, positive correlation (greater) at the usual confidence interval.
Histograms of volatility and an example of a time series for a 10-year bond, a histogram of estimated volatility for all 10-year bonds, b histogram of estimated volatility on auction days, c an example of an estimated volatility time series. The bond code is ES00000120G4, a 10-year bond. The vertical linesare auction days for this bond
Appendix 3: Empirical implications from the AM discriminatory auction
Figure 6 is analogous/similar to Figs. 2 and 3, in the main text.
Bid behavior, bidders’ profit and volatility for the \(AM^d\)’s model, a \(AM^d\) Avg Discount, b \(AM^d\) Avg Bid, c \(AM^d\) Avg Profit, d \(AM^d\) Std Discount, e \(AM^d\) Std Bid
Appendix 4: Scatter plots, residuals and ACF’s
Figures 7, 8 , 9, 10 and 11 present scatter plots of volatility versus the corresponding variable, and a plot and ACF of residuals, on panels (a), (b) and (c), respectively, for the variables for with volatility is significant on the empirical regressions. On panel (a) the scatter plot represent volatility on the horizontal axis and the corresponding variable on the vertical axis. The colors represent different bond types, with maturity increasing as the color shifts from green to red. Note that volatility and maturity are positively correlated: Green points are to the left, whereas red points are to right. The regression line illustrates a positive correlation between the variables. Panels (b) and (c) show no evidence of autocorrelation for the residuals.
Average bid spread, a Avg Bid Spread versus Volatility, b Residuals, c ACF
Average discount, a Avg discount versus volatility, b residuals, c ACF
Average profit, a Avg Profit versus Volatility, b Residuals, c ACF
Standard deviation of low bid, a Std Low Bid versus Volatility, b Residuals, c ACF
Standard deviation of discount, a Std Discount versus Volatility, b Residuals, c ACF
Rights and permissions
About this article
Cite this article
Alvarez, F., Mazón, C. Price volatility in the secondary market and bidders’ heterogeneous behavior in Spanish Treasury auctions. Empir Econ 50, 1435–1466 (2016). https://doi.org/10.1007/s00181-015-0988-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00181-015-0988-x