Skip to main content
SpringerLink
Log in

Bayesian model-based clustering for longitudinal ordinal data

  • Original Paper
  • Published:
Computational Statistics Aims and scope Submit manuscript

Abstract

Traditional cluster analysis methods used in ordinal data, for instance k-means and hierarchical clustering, are mostly heuristic and lack statistical inference tools to compare among competing models. To address this we propose a latent transitional model, a finite mixture model that includes both observed and latent covariates and apply it for the first time to the case of longitudinal ordinal data. This model-based clustering model is an extension of the proportional odds model and includes a first-order transitional term, occasion effects and interactions which provide flexible ways to capture different time patterns by cluster as well as time-heterogeneous transitions. We estimate model parameters within a Bayesian setting using a Markov chain Monte Carlo scheme and block-wise Metropolis–Hastings sampling. We illustrate the model using 2001–2011 self-reported health status (SRHS) from the Household, Income and Labour Dynamics in Australia survey. SRHS is recorded as an ordinal variable with five levels: poor, fair, good, very good and excellent. Using the Widely Applicable Information Criterion for model comparison, we find evidence for six latent groups. Transitions in the original data and the estimated groups are visualized using heatmaps.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  • Agresti A (2010) Analysis of ordinal categorical data, 2nd edn. Wiley series in probability and statistics. Wiley, London

    Book  Google Scholar 

  • Agresti A (2013) Categorical data analysis, 3rd edn. Wiley series in probability and statistics, 3rd edn. Wiley, London

    Google Scholar 

  • Albert J, Chib S (1995) Bayesian residual analysis for binary response regression models. Biometrika 82(4):747–769

    Article  MathSciNet  MATH  Google Scholar 

  • Arnold R, Hayakawa Y, Yip P (2010) Capture-recapture estimation using finite mixtures of arbitrary dimension. Biometrics 66(2):644–655

    Article  MathSciNet  MATH  Google Scholar 

  • Beaumont MA, Zhang W, Balding DJ (2002) Approximate Bayesian computation in population genetics. Genetics 162(4):2025–2035

    Google Scholar 

  • Biernacki C, Jacques J (2015) Model-based clustering of multivariate ordinal data relying on a stochastic binary search algorithm. Stat Comput 26:1–15

    MathSciNet  MATH  Google Scholar 

  • Biernacki C, Celeux G, Govaert G (2000) Assessing a mixture model for clustering with the integrated completed likelihood. IEEE Trans Pattern Anal Mach Intell 22(7):719–725

    Article  Google Scholar 

  • Celeux G, Forbes F, Robert CP, Titterington DM et al (2006) Deviance information criteria for missing data models. Bayesian Anal 1(4):651–673

    Article  MathSciNet  MATH  Google Scholar 

  • Cheon K, Thoma ME, Kong X, Albert PS (2014) A mixture of transition models for heterogeneous longitudinal ordinal data: with applications to longitudinal bacterial vaginosis data. Stat Med 33(18):3204–3213

    Article  MathSciNet  Google Scholar 

  • Dempster AP, Laird NM, Rubin DB (1977) Maximum likelihood from incomplete data via the em algorithm. J R Stat Soc 39(1):1–38

    MathSciNet  MATH  Google Scholar 

  • DeSantis SM, Houseman EA, Coull BA, Stemmer-Rachamimov A, Betensky RA (2008) A penalized latent class model for ordinal data. Biostatistics 9(2):249–262

    Article  MATH  Google Scholar 

  • DeYoreo M, Kottas A (2018) Bayesian nonparametric modeling for multivariate ordinal regression. J Comput Graph Stat 27(1):71–84

    Article  MathSciNet  MATH  Google Scholar 

  • Diggle PJ, Heagerty PJ, Liang KY, Zeger SL (2002) Analysis of longitudinal data, 2nd edn. Oxford University Press, Oxford

    MATH  Google Scholar 

  • Drton M, Plummer M (2017) A Bayesian information criterion for singular models. J R Stat Soc Ser B (Stat Methodol) 79(2):323–380

    Article  MathSciNet  MATH  Google Scholar 

  • Everitt B, Landau S, Leese M (2001) Cluster analysis. Arnold, London

    MATH  Google Scholar 

  • Fernández D, Arnold R (2016) Model selection for mixture-based clustering for ordinal data. Aust N Z J Stat 58(4):437–472

    Article  MathSciNet  MATH  Google Scholar 

  • Fernández D, Arnold R, Pledger S (2016) Mixture-based clustering for the ordered stereotype model. Comput Stat Data Anal 93:46–75

    Article  MathSciNet  MATH  Google Scholar 

  • Fraley C, Raftery AE (2002) Model-based clustering, discriminant analysis, and density estimation. J Am Stat Assoc 97(458):611–631

    Article  MathSciNet  MATH  Google Scholar 

  • Friel N, McKeone J, Oates CJ, Pettitt AN (2017) Investigation of the widely applicable Bayesian information criterion. Stat Comput 27(3):833–844

    Article  MathSciNet  MATH  Google Scholar 

  • Frühwirth-Schnatter S, Pamminger C, Weber A, Winter-Ebmer R (2012) Labor market entry and earnings dynamics: Bayesian inference using mixtures-of-experts Markov chain clustering. J Appl Econ 27(7):1116–1137

    Article  MathSciNet  Google Scholar 

  • Frydman H (2005) Estimation in the mixture of Markov chains moving with different speeds. J Am Stat Assoc 100(471):1046–1053

    Article  MathSciNet  MATH  Google Scholar 

  • Geisser S, Eddy WF (1979) A predictive approach to model selection. J Am Stat Assoc 74(365):153–160

    Article  MathSciNet  MATH  Google Scholar 

  • Gelman A, Rubin DB (1992) Inference from iterative simulation using multiple sequences. Stat Sci 7(4):457–472

    Article  MATH  Google Scholar 

  • Gelman A, Carlin JB, Stern HS, Dunson DB, Vehtari A, Rubin DB (2014a) Bayesian data analysis, 3rd edn. Taylor & Francis, London

    MATH  Google Scholar 

  • Gelman A, Hwang J, Vehtari A (2014b) Understanding predictive information criteria for Bayesian models. Stat Comput 24(6):997–1016

    Article  MathSciNet  MATH  Google Scholar 

  • Govaert G, Nadif M (2008) Block clustering with Bernoulli mixture models: comparison of different approaches. Comput Stat Data Anal 52:3233–3245

    Article  MathSciNet  MATH  Google Scholar 

  • Green PJ (1995) Reversible jump Markov chain monte carlo computation and Bayesian model determination. Biometrika 82(4):711–732

    Article  MathSciNet  MATH  Google Scholar 

  • Gutmann MU, Dutta R, Kaski S, Corander J (2018) Likelihood-free inference via classification. Stat Comput 28(2):411–425

    Article  MathSciNet  MATH  Google Scholar 

  • Hastings WK (1970) Monte carlo sampling methods using Markov chains and their applications. Biometrika 57(1):97–109

    Article  MathSciNet  MATH  Google Scholar 

  • Hui FKC, Warton DI, Ormerod JT, Haapaniemi V, Taskinen S (2017) Variational approximations for generalized linear latent variable models. J Comput Graph Stat 26(1):35–43

    Article  MathSciNet  Google Scholar 

  • Kass RE, Raftery AE (1995) Bayes factors. J Am Stat Assoc 90(430):773–795

    Article  MathSciNet  MATH  Google Scholar 

  • Kaufman L, Rousseeuw PJ (1990) Finding groups in data: an introduction to cluster analysis. Wiley, New York

    Book  MATH  Google Scholar 

  • Kedem B, Fokianos K (2005) Regression models for time series analysis, vol 488. Wiley, London

    MATH  Google Scholar 

  • Labiod L, Nadif M (2011) Co-clustering for binary and categorical data with maximum modularity. In: ICDM, pp 1140–1145

  • Liu I, Agresti A (2005) The analysis of ordered categorical data: an overview and a survey of recent developments. TEST 14(1):1–73

    Article  MathSciNet  MATH  Google Scholar 

  • MacQueen J (1967) Some methods for classification and analysis of multivariate observations. In: Neyman J, Cam LML (eds) Proceedings of the 5th Berkeley symposium on mathematical statistics and probability. University of California Press, Berkeley, pp 281–297

    Google Scholar 

  • Manly BF (2005) Multivariate statistical methods: a primer. CRC Press, Boca Raton

    MATH  Google Scholar 

  • Marin JM, Mengersen K, Robert CP (2005) Bayesian modelling and inference on mixtures of distributions. Handb Stat 25(16):459–507

    Article  MathSciNet  Google Scholar 

  • Matechou E, Liu I, Fernández D, Farias M, Gjelsvik B (2016) Biclustering models for two-mode ordinal data. Psycometrika 81(3):611–624

    Article  MathSciNet  MATH  Google Scholar 

  • McCullagh P (1980) Regression models for ordinal data. Stat Methodol 42:109–142

    MathSciNet  MATH  Google Scholar 

  • McCullagh P, Nelder JA (1989) Generalized linear models, 2nd edn. Chapman & Hall, London

    Book  MATH  Google Scholar 

  • McKinley TJ, Morters M, Wood JL et al (2015) Bayesian model choice in cumulative link ordinal regression models. Bayesian Anal 10(1):1–30

    Article  MathSciNet  MATH  Google Scholar 

  • McLachlan G, Peel D (2000) Finite mixture models. Wiley series in probability and statistics. Wiley, London

    Book  MATH  Google Scholar 

  • McNicholas PD (2016) Mixture model-based classification. Chapman and Hall, Boca Raton

    Book  MATH  Google Scholar 

  • Melnykov V, Maitra R (2010) Finite mixture models and model-based clustering. Stat Surv 4:1–274

    Article  MathSciNet  MATH  Google Scholar 

  • Metropolis N, Rosenbluth AW, Rosenbluth MN, Teller AH, Teller E (1953) Equation of state calculations by fast computing machines. J Chem Phys 21(6):1087–1092

    Article  Google Scholar 

  • Müller P, Quintana F, Jara A, Hanson T (2015) Bayesian nonparametric data analysis. Springer, Berlin

    Book  MATH  Google Scholar 

  • Pamminger C, Frühwirth-Schnatter S et al (2010) Model-based clustering of categorical time series. Bayesian Anal 5(2):345–368

    Article  MathSciNet  MATH  Google Scholar 

  • Pledger S (2000) Unified maximum likelihood estimates for closed capture–recapture models using mixtures. Biometrics 56:434–442

    Article  MATH  Google Scholar 

  • Pledger S, Arnold R (2014) Clustering, scaling and correspondence analysis: unified pattern-detection models using mixtures. Comput Stat Data Anal 71:241–261

    Article  MATH  Google Scholar 

  • R Core Team (2017) R: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna. https://www.R-project.org/

  • Richardson S, Green PJ (1997) On Bayesian analysis of mixtures with an unknown number of components. J R Stat Soc Ser B (Methodol) 59:731–792

    Article  MathSciNet  MATH  Google Scholar 

  • Robert CP, Casella G (2005) Monte Carlo statistical methods (Springer texts in statistics). Springer, Secaucus

    Google Scholar 

  • Spiegelhalter DJ, Best NG, Carlin BP, Van Der Linde A (2002) Bayesian measures of model complexity and fit. J R Stat Soc Ser B (Stat Methodol) 64(4):583–639

    Article  MathSciNet  MATH  Google Scholar 

  • Spiegelhalter DJ, Best NG, Carlin BP, Linde A (2014) The deviance information criterion: 12 years on. J R Stat Soc Ser B (Stat Methodol) 76(3):485–493

    Article  MathSciNet  MATH  Google Scholar 

  • Stephens M (2000) Dealing with label switching in mixture models. J R Stat Soc Ser B 62:795–809

    Article  MathSciNet  MATH  Google Scholar 

  • Stevens S (1946) On the theory of scales of measurement. Science 103(2684):677–680

    Article  MATH  Google Scholar 

  • Vehtari A, Gelman A, Gabry J (2017) Practical Bayesian model evaluation using leave-one-out cross-validation and waic. Stat Comput 27(5):1413–1432

    Article  MathSciNet  MATH  Google Scholar 

  • Wainwright M, Jordan M (2008) Graphical models, exponential families, and variational inference. Foundations and trends in machine learning. Now Publishers, New York

    MATH  Google Scholar 

  • Watanabe S (2009) Algebraic geometry and statistical learning theory. Cambridge University Press, Cambridge

    Book  MATH  Google Scholar 

  • Watanabe S (2013) A widely applicable Bayesian information criterion. J Mach Learn Res 14(1):867–897

    MathSciNet  MATH  Google Scholar 

  • Wilkinson L, Friendly M (2009) The history of the cluster heat map. Am Stat 63(2):179–184

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The work is being supported by the Marsden Fund Grants 16-VUW-062 and E2987-3648 from the Royal Society of New Zealand. We would like to thank Professor Shirley Pledger from Victoria University of Wellington for many useful discussions. This paper uses unit record data unit record data from the Household, Income and Labour Dynamics in Australia (HILDA) Survey. The HILDA Project was initiated and is funded by the Australian Government Department of Social Services (DSS) and is managed by the Melbourne Institute of Applied Economic and Social Research (Melbourne Institute). The findings and views reported here, however, are those of the author and should not be attributed to either DSS or the Melbourne Institute. More information about the HILDA survey can be found at: https://www.melbourneinstitute.com/hilda/.

Author information

Authors and Affiliations

  1. Institute for Molecular Bioscience and Queensland Alliance for Agriculture and Food Innovation, The University of Queensland, Brisbane, QLD, 4072, Australia

    Roy Costilla

  2. School of Mathematics and Statistics, Victoria University of Wellington, Wellington, New Zealand

    Ivy Liu, Richard Arnold & Daniel Fernández

  3. Institut de Recerca Sant Joan de Déu, Parc Sanitari Sant Joan de Déu, CIBERSAM, Barcelona, Spain

    Daniel Fernández

Authors
  1. Roy Costilla
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ivy Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Richard Arnold
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Daniel Fernández
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Roy Costilla.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

Appendix A: Proposals

After choosing initial values for all model parameters (\(\mu \), \(\alpha \), \(\beta \), \(\gamma \), \(\pi \), \(\sigma ^2_{\mu }\), \(\sigma ^2_{\alpha }\), \(\sigma ^2_{\beta }\), and \(\sigma ^2_{\gamma }\)), we proceed to update them according to the following:

$$\begin{aligned}&\mu '_k \mid \mu _k, \mu _{k-1}, \mu _{k+1} {\sim } U[ \text { max}(\mu _k - \tau ,\mu _{k-1}), \text { min}(\mu _k + \tau ,\mu _{k+1}) ] \; k=2, \ldots , q-1,\\&\quad \mu _0=-\infty ,\mu _1=0 \, \mu _q=\infty \\&\alpha '_r \mid \alpha _r \overset{iid}{\sim }\text {Normal}(\alpha _r,\sigma ^2_{\alpha p}) \qquad r=1, \ldots R, \\&\beta '_{rk'} \mid \beta _{rk'} \overset{iid}{\sim }\text {Normal}(\beta _{rk'},\sigma ^2_{\beta p}) \qquad k'=1, \ldots q-1, \; \beta _{rq}=-\sum _{k'=1}^{q-1}\beta _{rk'}, \; \forall r=1, \ldots R, \\&\gamma '_j \mid \gamma _j \overset{iid}{\sim }\text {Normal}(\gamma _j,\sigma ^2_{\gamma p}) \qquad j=2, \ldots p-1, \; \gamma _{p}=-\sum _{j=2}^{p-1}\gamma _j \\&\text {logit}(w') \mid \text {logit}(w) \sim \text {Normal}(\text {logit}(w), \sigma ^2_{\pi p}) \qquad w=\pi _{r1}/(\pi _{r1}+\pi _{r2}) \; r1,r2 \in {1, \ldots ,R} \\&\pi '_{r1}=w'(\pi _{r1}+\pi _{r2}) \qquad \pi '_{r2}=(1-w')(\pi _{r1}+\pi _{r2}) \\&\text {log}(\sigma '^2_{\mu }) \mid \text {log}(\sigma ^2_{\mu }) \sim \text {Normal}(\text {log}(\sigma ^2_{\mu }), \sigma ^{2}_{\sigma \mu p}) \\&\text {log}(\sigma '^2_{\alpha }) \mid \text {log}(\sigma ^2_{\alpha }) \sim \text {Normal}(\text {log}(\sigma ^2_{\alpha }), \sigma ^{2}_{\sigma \alpha p}) \\&\text {log}(\sigma '^2_{\beta }) \mid \text {log}(\sigma ^2_{\beta }) \sim \text {Normal}(\text {log}(\sigma ^2_{\beta }), \sigma ^{2}_{\sigma \beta p}) \\&\text {log}(\sigma '^2_{\gamma }) \mid \text {log}(\sigma ^2_{\gamma }) \sim \text {Normal}(\text {log}(\sigma ^2_{\gamma }), \sigma ^{2}_{\sigma \gamma p}) \end{aligned}$$

with proposal step sizes scaled by: \(\tau =0.5\), \(\sigma ^2_{\alpha p}=0.1\), \(\sigma ^2_{\beta p}=0.1\), \(\sigma ^2_{\gamma p}=0.1\), \(\sigma ^2_{\pi p}=0.25\), \(\sigma ^{2}_{\sigma \mu p}=\text {log}(2)\), \(\sigma ^{2}_{\sigma \alpha p}=\text {log}(4)\), \(\sigma ^{2}_{\sigma \beta p}=\text {log}(1.5)\) and \(\sigma ^{2}_{\sigma \gamma p}=\text {log}(2)\).

Appendix B: Posterior summary statistics and convergence diagnostics, HILDA case study \(R=6\)

Par

Median

Mean

SE

Lower CI

Upper CI

PSRF

\(\mu _2\)

3.53

3.54

0.24

3.12

4.04

1.00

\(\mu _3\)

6.86

6.87

0.27

6.35

7.38

1.00

\(\mu _4\)

11.06

11.06

0.33

10.46

11.73

1.00

\(\sigma ^2_{\mu }\)

0.27

0.34

0.25

0.08

0.74

1.00

\(\alpha _1\)

2.76

2.76

0.49

1.74

3.67

1.00

\(\alpha _2\)

5.02

4.99

0.33

4.40

5.60

1.04

\(\alpha _3\)

5.27

5.27

0.24

4.77

5.74

1.00

\(\alpha _4\)

8.20

8.17

0.53

7.47

9.15

1.10

\(\alpha _5\)

9.87

9.84

0.73

8.39

11.23

1.07

\(\alpha _6\)

12.39

12.40

1.02

10.17

14.64

1.06

\(\sigma ^2_{\alpha }\)

28.60

31.96

15.05

10.72

59.19

1.00

\(\beta _{11}\)

\(-\) 0.15

\(-\) 0.17

0.42

\(-\) 0.97

0.68

1.03

\(\beta _{12}\)

\(-\) 0.31

\(-\) 0.31

0.36

\(-\) 1.01

0.37

1.00

\(\beta _{13}\)

0.23

0.24

0.34

\(-\) 0.40

0.93

1.01

\(\beta _{14}\)

0.17

0.19

0.44

\(-\) 0.72

1.06

1.00

\(\beta _{15}\)

0.06

0.05

0.91

\(-\) 1.86

1.78

1.02

\(\beta _{21}\)

\(-\) 0.53

\(-\) 1.92

2.74

\(-\) 7.06

0.58

1.00

\(\beta _{22}\)

\(-\) 1.03

\(-\) 1.50

1.06

\(-\) 3.68

\(-\) 0.35

1.00

\(\beta _{23}\)

0.32

0.17

0.51

\(-\) 1.05

0.89

1.00

\(\beta _{24}\)

1.44

2.16

1.45

0.90

5.06

1.00

\(\beta _{25}\)

\(-\) 0.26

1.09

2.72

\(-\) 1.45

6.08

1.00

\(\beta _{31}\)

\(-\) 6.06

\(-\) 4.63

2.78

\(-\) 7.12

0.50

1.00

\(\beta _{32}\)

\(-\) 3.08

\(-\) 2.67

1.04

\(-\) 3.92

\(-\) 0.69

1.00

\(\beta _{33}\)

\(-\) 0.45

\(-\) 0.42

0.61

\(-\) 1.53

0.66

1.02

\(\beta _{34}\)

4.36

3.63

1.53

0.85

5.19

1.00

\(\beta _{35}\)

5.51

4.09

2.64

\(-\) 0.85

6.34

1.00

\(\beta _{41}\)

\(-\) 0.19

\(-\) 0.29

0.81

\(-\) 1.19

0.73

1.18

\(\beta _{42}\)

\(-\) 0.19

\(-\) 0.22

0.50

\(-\) 0.98

0.58

1.13

\(\beta _{43}\)

\(-\) 0.29

\(-\) 0.30

0.29

\(-\) 0.85

0.27

1.03

\(\beta _{44}\)

\(-\) 0.10

\(-\) 0.03

0.60

\(-\) 0.62

0.41

1.25

\(\beta _{45}\)

0.78

0.84

0.78

\(-\) 0.27

1.88

1.17

\(\beta _{51}\)

0.17

0.17

0.44

\(-\) 0.70

1.00

1.01

\(\beta _{52}\)

0.29

0.31

0.46

\(-\) 0.68

1.22

1.03

\(\beta _{53}\)

0.26

0.27

0.40

\(-\) 0.55

1.04

1.04

\(\beta _{54}\)

0.23

0.24

0.36

\(-\) 0.46

0.94

1.00

\(\beta _{55}\)

\(-\) 1.03

\(-\) 0.99

0.78

\(-\) 2.44

0.70

1.10

\(\beta _{61}\)

\(-\) 0.06

\(-\) 0.05

0.44

\(-\) 0.94

0.87

1.00

\(\beta _{62}\)

\(-\) 0.06

\(-\) 0.06

0.46

\(-\) 1.00

0.84

1.01

\(\beta _{63}\)

\(-\) 0.15

\(-\) 0.16

0.45

\(-\) 1.07

0.66

1.04

\(\beta _{64}\)

0.04

0.06

0.39

\(-\) 0.77

0.86

1.00

\(\beta _{65}\)

0.24

0.22

0.69

\(-\) 1.17

1.57

1.04

\(\sigma ^2_{\beta 1}\)

0.28

0.33

0.20

0.09

0.73

1.02

\(\sigma ^2_{\beta 2}\)

0.77

3.54

5.67

0.12

15.43

1.00

\(\sigma ^2_{\beta 3}\)

8.29

8.56

6.86

0.17

20.43

1.00

\(\sigma ^2_{\beta 4}\)

0.25

0.45

1.51

0.09

0.67

1.31

\(\sigma ^2_{\beta 5}\)

0.29

0.35

0.23

0.09

0.77

1.00

\(\sigma ^2_{\beta 6}\)

0.27

0.33

0.24

0.08

0.72

1.00

\(\gamma _{2}\)

0.42

0.42

0.14

0.15

0.69

1.00

\(\gamma _{3}\)

0.17

0.17

0.13

\(-\) 0.09

0.42

1.00

\(\gamma _{4}\)

0.04

0.04

0.13

\(-\) 0.20

0.28

1.00

\(\gamma _{5}\)

\(-\) 0.08

\(-\) 0.08

0.13

\(-\) 0.33

0.17

1.00

\(\gamma _{6}\)

0.06

0.06

0.13

\(-\) 0.19

0.29

1.00

\(\gamma _{7}\)

0.06

0.06

0.13

\(-\) 0.18

0.32

1.00

\(\gamma _{8}\)

\(-\) 0.02

\(-\) 0.02

0.12

\(-\) 0.27

0.20

1.00

\(\gamma _{9}\)

0.06

0.06

0.13

\(-\) 0.19

0.31

1.00

\(\gamma _{10}\)

\(-\) 0.24

\(-\) 0.24

0.13

\(-\) 0.48

0.01

1.00

\(\gamma _{11}\)

\(-\) 0.46

\(-\) 0.47

0.13

\(-\) 0.71

\(-\) 0.21

1.00

\(\sigma ^2_{\gamma }\)

0.16

0.17

0.07

0.07

0.31

1.00

\(\pi _1\)

0.08

0.08

0.02

0.04

0.13

1.01

\(\pi _2\)

0.32

0.31

0.06

0.20

0.40

1.03

\(\pi _3\)

0.26

0.27

0.05

0.19

0.37

1.00

\(\pi _4\)

0.24

0.24

0.04

0.16

0.33

1.15

\(\pi _5\)

0.05

0.06

0.04

0.02

0.13

1.32

\(\pi _6\)

0.04

0.04

0.01

0.01

0.07

1.08

log-like

\(-\) 2121

\(-\) 2121

4.54

\(-\) 2130

\(-\) 2113

1.03

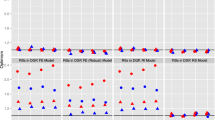
Appendix C: Traceplots and marginal posterior distributions, HILDA case study \(R=6\)

figure a

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Costilla, R., Liu, I., Arnold, R. et al. Bayesian model-based clustering for longitudinal ordinal data. Comput Stat 34, 1015–1038 (2019). https://doi.org/10.1007/s00180-019-00872-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00180-019-00872-4

Keywords

Search

Navigation