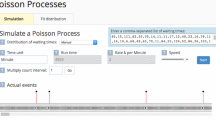
Abstract
Probability distributions are useful for modeling, simulation, analysis, and inference on varieties of natural processes and physical phenomena. There are uncountably many probability distributions. However, a few dozen families of distributions are commonly defined and are frequently used in practice for problem solving, experimental applications, and theoretical studies. In this paper, we present a new computational and graphical infrastructure, the Distributome, which facilitates the discovery, exploration and application of diverse spectra of probability distributions. The extensible Distributome infrastructure provides interfaces for (human and machine) traversal, search, and navigation of all common probability distributions. It also enables distribution modeling, applications, investigation of inter-distribution relations, as well as their analytical representations and computational utilization. The entire Distributome framework is designed and implemented as an open-source, community-built, and Internet-accessible infrastructure. It is portable, extensible and compatible with HTML5 and Web2.0 standards (http://Distributome.org). We demonstrate two types of applications of the probability Distributome resources: computational research and science education. The Distributome tools may be employed to address five complementary computational modeling applications (simulation, data analysis and inference, model-fitting, examination of the analytical, mathematical and computational properties of specific probability distributions, and exploration of the inter-distributional relations). Many high school and college science, technology, engineering and mathematics (STEM) courses may be enriched by the use of modern pedagogical approaches and technology-enhanced methods. The Distributome resources provide enhancements for blended STEM education by improving student motivation, augmenting the classical curriculum with interactive webapps, and overhauling the learning assessment protocols.






Similar content being viewed by others
References
Abrahams M-R et al (2009) Quantitating the multiplicity of infection with human immunodeficiency virus type 1 subtype C reveals a non-poisson distribution of transmitted variants. J Virol 83(8):3556–3567
Allen PR (2005) The substellar mass function: a Bayesian approach. Astrophys J 625:385–397
Ambrose PG, Grasela DM (2000) The use of Monte Carlo simulation to examine pharmacodynamic variance of drugs: fluoroquinolone pharmacodynamics against Streptococcus pneumoniae. Diagn Microbiol Infect Dis 38(3):151–157
Babuka I, Nobile F, Tempone R (2007) Reliability of computational science. Numer Methods Partial Differ Equ 23(4):753–784
Balakrishnan N, Basu AP (1995) The exponential distribution: theory, methods and applications. CRC Press, Boca Raton
Binder K, Heermann DW (2010) Monte Carlo simulation in statistical physics: an introduction, vol 80. Springer, Berlin
Chakak A, Koehler K (1995) A strategy for constructing multivariate distributions. Commun Stat Simul Comput 24(3):537–550
Consortium for the Advancement of Undergraduate Statistics Education (CAUSE) (2013). Available from: www.causeweb.org
Couto P (2003) Assessing the accuracy of spatial simulation models. Ecol Model 167(1–2):181–198
Cramer H (2004) Random variables and probability distributions. Cambridge University Press, Cambridge
Dinov I (2006) SOCR: statistics online computational resource. J Stat Softw 16(1):1–16
Dinov I (2006) Statistics online computational resource. J Stat Softw 16(1):1–16
Dinov I, Christou N, Sanchez J (2008) Central limit theorem: new SOCR applet and demonstration activity. J Stat Educ 16(2):1–12
Dobyns WB et al (2004) Inheritance of most X-linked traits is not dominant or recessive, just X-linked. Am J Med Genet A 129(2):136–143
Dvison A, Hinkley DV, Schechtman E (1986) Efficient bootstrap simulation. Biometrika 73(3):555–566
Eberhard OV (1992) The S-distribution a tool for approximation and classification of univariate. Unimodal Prob Distrib Biometrical J 34(7):855–878
Eddelbuettel D, François R (2011) Rcpp: seamless R and C++ integration. J Stat Softw 40(8):1–18
Etienne RS, Olff H (2005) Confronting different models of community structure to species-abundance data: a Bayesian model comparison. Ecol Lett 8(5):493–504
Ferguson TS (1996) A course in large sample theory. Chapman and Hall, London
Forbes C et al (2011) Statistical distributions. Wiley Online Library, Hoboken
Frank SA, Smith E (2011) A simple derivation and classification of common probability distributions based on information symmetry and measurement scale. J Evol Biol 24(3):469–484
Freedman D et al (2005) Model-based segmentation of medical imagery by matching distributions. Med Imaging IEEE Trans 24(3):281–292
Galvão RD, Chiyoshi FY, Morabito R (2005) Towards unified formulations and extensions of two classical probabilistic location models. Comput Oper Res 32(1):15–33
Gardiner CW (2009) Stochastic methods. Springer, Berlin
Gelman A et al (2010) Handbook of Markov chain Monte Carlo: methods and applications. Chapman & Hall/CRC, London
Giot L et al (2003) A protein interaction map of Drosophila melanogaster. Science 302(5651):1727–1736
Gokhale S, Khare M (2007) Statistical behavior of carbon monoxide from vehicular exhausts in urban environments. Environ Model Softw 22(4):526–535
Guisan A, Edwards TC, Hastie T (2002) Generalized linear and generalized additive models in studies of species distributions: setting the scene. Ecol Model 157(2–3):89–100
Jackwerth JC, Rubinstein M (1996) Recovering probability distributions from option prices. J Finance 51(5):1611–1631
Jara A et al (2011) DPpackage: Bayesian non-and semi-parametric modelling in R. J Stat Softw 40(5):1
Johnson NL, Kotz S, Balakrishnan N (1995) Continuous univariate distributions, vol 2. Wiley, New York
Jones MC (2004) Families of distributions arising from distributions of order statistics (with discussion). TEST 13:1–43
Kelton WD, Law AM (2000) Simulation modeling and analysis. McGraw Hill, Boston
Kittur A, Chi EH, Suh B (2009) What’s in Wikipedia? Mapping topics and conflict using socially annotated category structure. In: Proceedings of the SIGCHI conference on human factors in computing systems. ACM
Kogan V, Rind T (2011) Determining critical power equipment inventory using extreme value approach and an auxiliary Poisson model. Comput Ind Eng 60(1):25–33
Lappin G, Temple S (2006) Radiotracers in drug development. CRC/Taylor & Francis, Boca Raton
Le S, Josse J, Husson F (2008) FactoMineR: an R package for multivariate analysis. J Stat Softw 25(1):1–18
Lee K-I et al (2012) Variation in stress resistance patterns among stx genotypes and genetic lineages of shiga toxin-producing Escherichia coli O157. Appl Environ Microbiol 78(9):3361–3368
Leemis LM, McQueston JT (2008) Univariate distribution relationships. Am stat 62:45–53
Leo WR (1994) Techniques for nuclear and particle physics experiments: a how-to approach. Springer, Berlin
Lou S-J et al (2011) The impact of problem-based learning strategies on STEM knowledge integration and attitudes: an exploratory study among female Taiwanese senior high school students. Int J Technol Des Educ 21(2):195–215
Manders KL (1986) What numbers are real? In: PSA: proceedings of the biennial meeting of the Philosophy of Science Association, 1986, pp 253–269
Milne D, Witten IH (2012) An open-source toolkit for mining Wikipedia. Artif Intell. 194:222–239. http://www.sciencedirect.com/science/article/pii/S000437021200077X
Mooney CZ (1997) Monte carlo simulation, vol 116. Sage, California Incorporated
Musa JD, Okumoto K (1984) A logarithmic Poisson execution time model for software reliability measurement. In: Proceedings of the 7th international conference on Software engineering. IEEE Press
Nadarajah S (2007) Statistical distributions of potential interest in ultrasound speckle analysis. Phys Med Biol 52:N213–N227
Newman MEJ (2002) Assortative mixing in networks. Phys Rev Lett 89(20):208701
Nichols TE et al (2002) Spatiotemporal reconstruction of list-mode PET data. Med Imaging IEEE Trans 21(4):396–404
Panfilo G, Tavella P, Zucca C, (2004) Stochastic processes for modelling and evaluating atomic click behavious. In: Ciarlini P, Cox MG, Pavese FG (eds) Advanced mathematical & computational tools in metrology VI
Plerou V et al (1999) Scaling of the distribution of price fluctuations of individual companies. Phys Rev E 60(6):6519
Qiao F, Yang H, Lam WHK (2001) Intelligent simulation and prediction of traffic flow dispersion. Transp Res B Methodol 35(9):843–863
Ramírez P, Carta JA (2005) Influence of the data sampling interval in the estimation of the parameters of the Weibull wind speed probability density distribution: a case study. Energy Convers Manag 46(15–16):2419–2438
Ripley BD (2009) Stochastic simulation, vol 316. Wiley, New York
Rubinstein RY, Kroese DP (2011) Simulation and the Monte Carlo method, vol 707. Wiley, New York
Rule G, Bajzek D, Kessler A (2010) Molecular visualization in STEM education: leveraging Jmol in an integrated assessment platform. In: World conference on E-learning in corporate, government, healthcare, and higher education
Sarovar M et al (2004) Practical scheme for error control using feedback. Phys Rev A 69(5):052324
Siegrist K (2004) The probability/statistics object library. J Online Math Its Appl 4:1–12
Song WT (2005) Relationships among some univariate distributions. IIE Trans 37(7):651–656
Talamo A, Gohar Y (2008) Production of medical radioactive isotopes using KIPT electron driven subcritical facility. Appl Radiat Isot 66(5):577–586
Traboulsi EI (2012) Genetic diseases of the eye, 2nd edn. OUP, USA
Train K (2009) Discrete choice methods with simulation. Cambridge University Press, Cambridge
Uppal R, Wang T (2003) Model misspecification and underdiversification. J Finance 58(6):2465–2486
Van den Hoff J (2005) Principles of quantitative positron emission tomography. Amino Acids 29(4):341–353
Wald A (1949) Note on the consistency of the maximum likelihood estimate. Ann Math Stat 20(4):595–601
Weidlich W (2003) Sociodynamics-a systematic approach to mathematical modelling in the social sciences. Chaos Solitons Fractals 18(3):431–437
Wolfram S (1999) The MATHEMATICA\({\textregistered }\) book, version 4. Cambridge University Press, Cambridge
Acknowledgments
The development of the Distributome infrastructure was partially supported by NSF Grants, 1023115, 1022560, 1022636, 0089377, 9652870, 0442992, 0442630, 0333672, 0716055, and by NIH Grants U54 RR021813, P20 NR015331, U54 EB020406, P50 NS091856, and P30 DK089503.
Significant contributions from Lawrence Moore, David Aldous, Robert Dobrow and James Pitman ensured that the Distributome infrastructure is generic, complete and extensible. The authors also thank Syed Husain, Selvam Palanimalai, John Guo Jun, Philip Chu, Yunzhong He, Yunzhu He, Prarthana Alevoor and Shelley Zhou Yuhao for their ideas and help with development and validation of the Distributome infrastructure. Glen Marian proofread the final manuscript. Journal referees and editorial staff provided valuable suggestions that improved the manuscript.
Conflict of interest
The authors do not have potential conflicts of interest outside of the funding sources referred to in the acknowledgment section. Ethical Standard The results of this research did not involve human participants, animals, or data derived from human or animal studies.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Dinov, I.D., Siegrist, K., Pearl, D.K. et al. Probability Distributome: a web computational infrastructure for exploring the properties, interrelations, and applications of probability distributions. Comput Stat 31, 559–577 (2016). https://doi.org/10.1007/s00180-015-0594-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00180-015-0594-6