Robust likelihood inference for multivariate correlated count data

Abstract

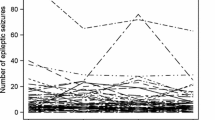
A parametric robust approach for analyzing correlated count data is introduced. This method enables one to construct an asymptotically valid likelihood for the regression parameter when knowledge about the joint distribution for data is scarce or not available. We use simulations and real data analysis to demonstrate the merit of the proposed robust likelihood method.

Appendix: The I and V terms

The two matrices I and V required to calculate the amendment that robustifies the naïve likelihood function are simply the Fisher information matrix and the variance matrix of the score functions. Their derivation is straightforward and routine. Following the definitions, one can show that the matrix I consists of entries

$$\begin{aligned} I(\beta _r ,\beta _r )= & {} \mathop {\lim }\limits _{m\rightarrow \infty } \frac{1}{m}\sum _{i=1}^m {\left[ {\sum _{j=1}^{n_i} {\frac{1}{\mu _{ij}}{g}'(\eta _{ij} )^{2}x_{ij,r}^2 -\frac{{{\phi }}}{1+{{\phi }} \mu _{i+} }\left\{ {\sum _{j=1}^{n_i} {{g}'(\eta _{ij} )x_{ij,r}}} \right\} ^{2}}} \right] } ,\\&r=0,\ldots ,p-1, \end{aligned}$$

$r,s=0,\ldots ,p-1,$ and

The components of the matrix V are

$$\begin{aligned} V(\beta _r ,\beta _r )= & {} \mathop {\lim }\limits _{m\rightarrow \infty } \frac{1}{m}\sum _{i=1}^m {\left[ {\sum _{j=1}^{n_i} {Var\left( {\frac{Y_{ij}}{\mu _{ij}}-\frac{{{\phi }} S_i }{1+{{\phi }} \mu _{i+}}} \right) }} \right. } \left\{ {{g}'(\eta _{ij} )x_{ij,r}} \right\} ^{2} \\&\quad +\,2\mathop {\mathop {\sum }\limits _{k,l}}\limits _{{k<l}} \left\{ {\frac{Cov(Y_{ik} ,Y_{il} )}{\mu _{ik} \mu _{il}}-Cov\left( {\frac{Y_{ik}}{\mu _{ik}}+\frac{Y_{il}}{\mu _{il}},\frac{{{\phi }} Y_{i+}}{(1+{{\phi }} \mu _{i+} )}} \right) } \right. \\&\quad \qquad \qquad \quad \left. \left. {+Var\left( {\frac{{{\phi }} Y_{i+}}{1+{{\phi }} \mu _{i+} }} \right) } \right\} {g}'(\eta _{ik} ){g}'(\eta _{il} )x_{ik,r} x_{il,r} \right] ,\\&r=0,\ldots ,p-1 \\ V(\beta _r ,\beta _s )= & {} \mathop {\lim }\limits _{m\rightarrow \infty } \frac{1}{m}\sum _{i=1}^m {\left[ {\sum _{j=1}^{n_i} {Var\left( {\frac{Y_{ij}}{\mu _{ij}}-\frac{{{\phi }} S_i }{1+{{\phi }} \mu _{i+}}} \right) }} \right. } {g}'(\eta _{ij} )^{2}x_{ij,r} x_{ij,s} \\&\quad +\mathop {\mathop {\sum }\limits _{k,l}}\limits _{{k<l}} \left\{ {\frac{Cov(Y_{ik} ,Y_{il} )}{\mu _{ik} \mu _{il} }-Cov\left( {\frac{Y_{ik}}{\mu _{ik}}+\frac{Y_{il}}{\mu _{il} },\frac{{{\phi }} Y_{i+}}{(1+{{\phi }} \mu _{i+} )}} \right) } \right. \\&\quad \qquad \qquad \left. {\left. {+Var\left( {\frac{{{\phi }} Y_{i+}}{1+{{\phi }} \mu _{i+} }} \right) } \right\} {g}'(\eta _{ik} ){g}'(\eta _{il} )\left( {x_{ik,r} x_{il,s} +x_{il,r} x_{ik,s}} \right) } \right] ,\\&r\ne s=0,\ldots ,p-1 . \end{aligned}$$