The exact bootstrap method shown on the example of the mean and variance estimation

Abstract

The bootstrap method is based on resampling of the original randomsample drawn from a population with an unknown distribution. In the article it was shown that because of the progress in computer technology resampling is actually unnecessary if the sample size is not too large. It is possible to automatically generate all possible resamples and calculate all realizations of the required statistic. The obtained distribution can be used in point or interval estimation of population parameters or in testing hypotheses. We should stress that in the exact bootstrap method the entire space of resamples is used and therefore there is no additional bias which results from resampling. The method was used to estimate mean and variance. The comparison of the obtained distributions with the limit distributions confirmed the accuracy of the exact bootstrap method. In order to compare the exact bootstrap method with the basic method (with random sampling) probability that 1,000 resamples would allow for estimating a parameter with a given accuracy was calculated. There is little chance of obtaining the desired accuracy, which is an argument supporting the use of the exact method. Random sampling may be interpreted as discretization of a continuous variable.

1 Introduction

Consider random variable $X$ with unknown distribution $F$. We are interested in the distribution parameter denoted by $\theta$. If the parameter can not be constructed directly, it is necessary to draw a random sample and select an appropriate estimator of parameter $\theta$. The estimator is a statistic defined on a sample space. The random sample is denoted by ${\mathbf X} = (X_{1}, X_{2},{\ldots }, X_{n})$, its realization by ${\mathbf x} = (x_{1}, x_{2}, {\ldots }, x_{n})$, and the estimator of parameter $\theta$ by $\hat{{\theta }}=t({\mathbf X})$.

Efron (1979) proposed what he called the bootstrap method. It is based on a random selection of resamples (bootstrap samples) of size $n$ from the obtained sample (original sample) x. The random selection is done with replacement and is assumed to have identical probabilities equal to 1/$n$ of randomly selecting each of the values $x_{k}$, for $k=1, {\ldots }, n$. Thus, distribution $\hat{{F}}$, also known as the bootstrap distribution, is generated.

The bootstrap sample is denoted by ${\mathbf X}^{*}=\left( {X_1^*,X_2^*,\ldots ,X_n^*} \right)$, and its arbitrary realization by ${\mathbf x}^{*}=\left( {x_1^*,x_2^*,\ldots ,x_n^*} \right)$. Estimator $\hat{{\theta }}$ for the bootstrap sample is denoted by $\hat{{\theta }}^*=t\left( {{\mathbf X}^*} \right)$.

Approximation of the distribution of statistic $\hat{{\theta }}$ by the bootstrap statistic $\hat{{\theta }}^*$ is the essence of this method. If Monte Carlo approximation is used to construct distribution $\hat{{\theta }}^*$, it is necessary to determine the number of the randomly selected bootstrap samples $B$.

Using the bootstrap variance, Efron (1987) states that it is sufficient to have a small number of random samplings in order to achieve sufficient accuracy. Booth and Sarkar (1988) disagree with this statement. They used the distribution approximation of relative bootstrap variance. This allowed for the estimation of $B$ for the given error level at the assumed confidence level. It proved that achieving an error lower than 10 % at the 0.95 confidence level requires $B$ to be around 800. (Efron and Tibshirani (1993), p. 52) believe that the estimation of standard error rarely requires more than 200 replications (repeated random samplings) while estimating the confidence interval requires 1,000 replications (Efron and Tibshirani 1993, p. 162).

Having $B$ bootstrap samples ${\mathbf x}^{*1}, {\mathbf x}^{*2}, {\ldots }, {\mathbf x}^{*B}$, we may estimate the unknown parameter of population $\theta$. Each of these samples allows for calculating a single realization for statistic $\hat{{\theta }}^*$. For the given original sample the realization of this statistic for every $b$ resample is as follows:

$$\begin{aligned} \hat{{\theta }}^{*}\left( b \right)=t\left( {{\mathbf x}^{* b }} \right). \end{aligned}$$

(1)

The bootstrap estimation of parameter $\theta$ will then be:

$$\begin{aligned} \hat{{\theta }}^{*}\left( {\bullet } \right)=\frac{1}{B}\sum _{b=1}^B {\hat{{\theta }}^{*}\left( b \right)}, \end{aligned}$$

(2)

an estimation of the standard error of estimate will be a standard deviation in the form:

$$\begin{aligned} s^{*}=\sqrt{\frac{1}{B}\sum _{b=1}^B {\left( {\hat{{\theta }}^{*}\left( b \right)-\hat{{\theta }}^{*}\left( {\bullet } \right)} \right)^{2}} } \end{aligned}$$

(3)

or:

$$\begin{aligned} \hat{{s}}^{*}=\sqrt{\frac{1}{B-1}\sum _{b=1}^B {\left( {\hat{{\theta }}^{*}\left( b \right)-\hat{{\theta }}^{*}\left( {\bullet } \right)} \right)^{2}} } \end{aligned}$$

(4)

depending on whether $B$ includes all possible samples (3) or it is only their subset (4).

Considering the bootstrap method one may ask the question whether random sampling of the bootstrap sample ${\mathbf X}^{*}$ from the original sample X obtained previously is necessary. Random sampling is necessary if examining the entire population data is impossible or too costly. Using a sample instead of the population has its significant implications in the area of mathematical statistics interest.

Note that the fundamental sample property is its finite size. The given bootstrap distribution $\hat{{F}}$ for this sample is a simple discrete distribution. Distribution of any given statistic determined for $n$ discrete random variables with a finite number of realizations does not have to be estimated as it may simply be calculated. The only question that remains open is how many calculations are required in this approach, which will be discussed below.

Consider the case of the two-element sample ($x_{1}$, $x_{2})$. The possible resamples that may be obtained are: ($x_{1}$, $x_{1})$, ($x_{2}$, $x_{2})$, ($x_{1}$, $x_{2})$, ($x_{2}$, $x_{1})$. The probability of randomly selecting each of them is the same and equals 1/4. For the three-element sample ($x_{1}$, $x_{2}$, $x_{3})$ there are $3^{3}$ = 27 of resamples: ($x_{1}$, $x_{1}$, $x_{1})$, ($x_{1}$, $x_{1}$, $x_{2})$, ($x_{1}$, $x_{1}$, $x_{3})$, ($x_{1}$, $x_{2}$, $x_{1})$, ($x_{1}$, $x_{2}$, $x_{2})$, ($x_{1}$, $x_{2}$, $x_{3})$, ($x_{1}$, $x_{3}$, $x_{1})$, ($x_{1}$, $x_{3}$, $x_{2})$, ($x_{1}$, $x_{3}$, $x_{3})$, ($x_{2}$, $x_{1}$, $x_{1})$, ($x_{2}$, $x_{1}$, $x_{2})$, ($x_{2}$, $x_{1}$, $x_{3})$, ($x_{2}$, $x_{2}$, $x_{1})$, ($x_{2}$, $x_{2}$, $x_{2})$, ($x_{2}$, $x_{2}$, $x_{3})$, ($x_{2}$, $x_{3}$, $x_{1})$, ($x_{2}$, $x_{3}$, $x_{2})$, ($x_{2}$, $x_{3}$, $x_{3})$, ($x_{3}$, $x_{1}$, $x_{1})$, ($x_{3}$, $x_{1}$, $x_{2})$, ($x_{3}$, $x_{1}$, $x_{3})$, ($x_{3}$, $x_{2}$, $x_{1})$, ($x_{3}$, $x_{2}$, $x_{2})$, ($x_{3}$, $x_{2}$, $x_{3})$, ($x_{3}$, $x_{3}$, $x_{1})$, ($x_{3}$, $x_{3}$, $x_{2})$ i ($x_{3}$, $x_{3}$, $x_{3})$. The probability of selecting each of the aforementioned resamples is also the same and equals 1/27. The fact that the resamples include the same elements which are just permutated has no significance as each of them has a defined (identical) probability.

If the original sample is an $n$ element sample, then the number of equally probable resamples equals $BE = n^{n}$. The probability of randomly selecting each of the resamples is equal to 1/BE. It is necessary to stress that the space of resamples is a finite space measuring BE and such is the size of the exact (ideal) bootstrap sample. If it is not too large, all realizations of the estimator may be calculated. These realizations may be interpreted as realizations of a given discrete random variable. Since the number of the realizations is finite, it is necessary to use descriptive statistics tools for their analysis (estimation error is then calculated using formula (3)). If it is impossible to generate the entire sample space of resamples as $n^{n}$ is too large, random sampling, that is using the classical bootstrap (estimation error is described by formula (4)), is then necessary. It is worth noting that if the estimator is the mean and the sample is large, according to the Central Limit Theorem, there will be normal asymptotic distribution.

The bootstrap method which uses the entire space of resamples may be called the exact bootstrap method. The claim that the method is exact only pertains to resampling. With regard to the original sample, its adequacy in relation to the original variable $X$ is based on the Glivenko-Cantelli Theorem.

2 The exact bootstrap method

Let us assume that from the population described by random variable $X$ with an unknown distribution of probability $F$, an $n$ element primary sample ${\mathbf x} = (x_{1}, x_{2}, {\ldots }, x_{n})$ was drawn. Because for some $i\ne j$ it is possible that $x_{i}=x_{j}$, we should reduce¹ the size of the random sample to $k$ different values. The probabilities $p_{i}$ of achieving the realization $x_{i}$, for $i=1, 2, {\ldots }, k$ does not have to be identical for all $i$ (as is the case with the classical bootstrap).

Let us introduce the concept of a discrete random sample variable, which may be denoted by $X^{D}$, with probability distribution $F^{D}$ described using values $p_{i}$ such that:

$$\begin{aligned} p_i^\mathrm{D } =P\left( {X^\mathrm{D}=x_i } \right)=p_i ,\quad \text{ for}\quad i= \text{1}, \text{2},\ldots ,k. \end{aligned}$$

(5)

The distribution of random variable $X^{D}$ is equivalent to the bootstrap distribution $\hat{{F}}$. The resample is denoted by ${\mathbf X}^{\mathrm{D}}=\left( {X_1^\mathrm{D} ,X_2^\mathrm{D} ,\ldots ,X_n^\mathrm{D} } \right)$. Estimator $\hat{{\theta }}^{*}$ for the resample may be denoted by $\hat{{\theta }}^{\mathrm{D}}=t\left( {{\mathbf X}^\mathrm{D}} \right)$. The distribution of $\hat{{\theta }}$ will be approximated by the distribution of statistic $\hat{{\theta }}^\mathrm{D}$. Note that the problems related to the possible bias, consistency and effectiveness of the estimator pertain to estimator $\hat{{\theta }}$. In the exact bootstrap method the realizations of estimator $\hat{{\theta }}^{\mathrm{D}}$ are calculated (for the whole population of resamples) rather than estimated based on the sample (drawn from population of resamples). Therefore, the method does not introduce any additional bias.

For a single $b$ realization of the resample ${\mathbf x}^{\text{ D} b}=\left( {x_1^{\mathrm{D }b} ,x_2^{\text{ D} b} ,\ldots ,x_n^{\text{ D} b} } \right)$ we should calculate $\hat{{\theta }}^\mathrm{D}\left( b \right)=t\left( {{\mathbf x}^{\mathrm{D }b}} \right)=t\left( {x_1^{\mathrm{D }b} ,x_2^{\mathrm{D }b} ,\ldots ,x_n^{\mathrm{D }b} } \right)$ as well as the probability of its random selection. The probabilities are no longer identical due to the size reduction of the random sample for $k$ different values. The probability of selecting a $b$ sample equals:

$$\begin{aligned} p^{D b}=P\left( {\hat{{\theta }}^\mathrm{D}=\hat{{\theta }}^\mathrm{D}\left( b \right)} \right)=\prod _{i=1}^n {p_i^{\text{ D} b} } , \end{aligned}$$

(6)

where: $p_i^{\text{ D} b} =P\left( {X^\mathrm{D}=x_i^\mathrm{D b} } \right)$. The number of possible realizations of resamples equals $BE = k^{n}$.

The correct algorithm should satisfy the condition: $\sum \nolimits _{b=1}^{BE} {p^\mathrm{D} b} =1$.

Formula (6) describes the distribution of estimator $\hat{{\theta }}^\mathrm{D}$, which is used to approximate the distribution of estimator $\hat{{\theta }}$. It is a discrete distribution with a finite number of realizations although in most cases the number is very high. This distribution may be used in point or interval assessment of parameter $\theta$ or in testing hypotheses.

Note that in essence the entire operation is based on the approximation of an unknown continuous distribution of a certain random variable $\hat{{\theta }}$ using discrete random variable $\hat{{\theta }}^\mathrm{D}$ with a distribution which may be generated based on a sample. Through random sampling we actually conduct discretization of a certain continuous occurrence. We attempt to approximate the continuous random variable $X$ by a sequence of its realization ${\mathbf x} = (x_{1}, x_{2}, {\ldots }, x_{n})$. Knowing the distribution of the discrete random variable, we may automatically calculate the distribution of the function of this variable. In the case of continuous random variables there is no automatic method which would allow for calculating the distribution of these functions.

When using the bootstrap methods it is worth comparing the value of BE (the number of all resamples) with the prescribed number of resamplings $B$ in the classical bootstrap. For example, for $k=15$ and $n=18$ we obtain $BE =15^{18}$, which is a very large number, significantly greater than the sample $B=1{,}000$. Nowadays such a great number of repetitions can be generated. The pioneering work of Efron dates back to 1979. At that time conducting such a great number of calculations within a reasonable time was impossible. Since it was impossible to examine the entire “population” represented by the original sample, it was necessary to draw resamples from a “sample functioning as a population.”

In the bootstrap method the sequence of the obtained values of the estimator is sequenced from the lowest to the highest, which allows one to, for example, set the confidence intervals using the percentile method (Efron and Tibshirani 1993). In theory, the exact bootstrap method also permits it. The number of the possible realizations of statistic $\hat{{\theta }}^\mathrm{D}$ is very high. However, firstly, a part of the realizations of discrete statistic will certainly be repeated and secondly, it is advisable to group the results in a histogram. Creating a histogram is necessary for large problems, as the number of the possible estimator realizations is very large. However, this may cause a loss of data. We should also stress that in spite of this, a very accurate estimation of the confidence intervals may be achieved through the exact bootstrap method as the widths of the intervals in the histogram do not have to be identical. In ranges that require exact probabilities (or cumulative distribution function), the width of the interval may be very small. Limited accuracy may only result from the density of the individual realizations of the estimator and the probability of their selection.

The easiest method of generating all resamples for discrete distribution is the recursive drawing of sequential elements from the original sample of size $n$ (or $k$ if there are repetitions in the original sample). Such an algorithm may be included in the brute force category. Algorithms of this type are considered ineffective.

The number of generated realizations of the bootstrap samples may be reduced, as in resampling some values will be repeated—random sampling with repetitions. (Feller (1950), p. 38) presents a similar problem. Fisher and Hall (1991) presented an algorithm which allows for generating all resamples. Both works pertain to the situation when the probability of drawing every element from a sample is the same.

Every $n$ element secondary bootstrap sample, with the assumption of $k$ different values, from which we draw its elements may be written as:

$$\begin{aligned} {\mathbf x}^\mathrm{D }b=\left( {a_{1b} \times x_1 ,a_{2b} \times x_2 ,\ldots ,a_{kb} \times x_k } \right), \end{aligned}$$

(7)

where every $a_{jb} \ge 0$, for $j= 1, 2, {\ldots }, k$, is the number of occurrences in sample $b$ of a $j$ element of the sample. The numbers must satisfy the following condition:

$$\begin{aligned} \sum _{j=1}^k {a_{jb} } =n, \end{aligned}$$

(8)

whereby some of them may be equal to 0. If for the selected $j$ there is $a_{jb}=0$, it is an indication of the fact that $x_{j }$ did not occur in a $b$ resample.

The probability of drawing a single sample defined by (7) equals:

$$\begin{aligned} p^{\mathrm{D}b}=\prod _{j=1}^k {\left( {p_j^{\mathrm{D}b} } \right)^{a_{jb} }}. \end{aligned}$$

(9)

There are two compiled programs written in C++ posted on the following website: http://mors.sggw.waw.pl/~jkisielinska. The first one generates the exact bootstrap distribution of the mean estimator:

$$\begin{aligned} \bar{{X}}=\frac{1}{n}\sum _{i=1}^n {X_i }. \end{aligned}$$

(10)

The second generates the variance estimator:

$$\begin{aligned} \hat{{S}}^{2}=\frac{1}{n-1}\sum _{i=1}^n {\left( {X_i -\bar{{X}}} \right)^{2}}. \end{aligned}$$

(11)

The first program provides all the possible bootstrap realizations of the mean estimator, while the second one generates a histogram due to a very large number of realizations.

3 The limit distribution of the bootstrap sample mean and variance estimator

The exact bootstrap method will be used to estimate the mean and variance. The verification of accuracy will be made possible through the limit distributions which may be used when the sample is large ($n \ge 30$).

Consider an $n$ element random sample ${\mathbf X} = (X_{1}, X_{2},{\ldots }, X_{n})$. Variables $X_{i}$, for i=1, 2,..., $n$ have the same distributions $F$, with the expected value $\mu$ and standard deviation $\sigma$.

The limit distribution of the mean estimator $\bar{{X}}$ defined by formula (10) is a normal distribution with the following parameters:

$$\begin{aligned} \mu _{\bar{{X}}} =\mu ;\quad \sigma _{\bar{{X}}} =\frac{\sigma }{\sqrt{n}}. \end{aligned}$$

(12)

Before we define the limit distribution of an unbiased variance estimator (11) we will present the limit distribution of a biased estimator:

$$\begin{aligned} S^{2}=\frac{1}{n}\sum _{i=1}^n {\left( {X_i -\bar{{X}}} \right)^{2}}. \end{aligned}$$

(13)

The expected value of this estimator equals:

$$\begin{aligned} \mu _{S^{2}} =\frac{n-1}{n}\sigma ^{2}. \end{aligned}$$

(14)

If random variable $X$ has distribution N($\mu ,\sigma$), the distribution of the variance estimator (13) is a normal asymptotic distribution with the mean given (14) and standard deviation:

$$\begin{aligned} \sigma _{S^{2}}^{Norm} =\sqrt{\frac{2}{n}\cdot \sigma ^{4}}. \end{aligned}$$

(15)

The variance limit distribution from sample $S^{2 }$ drawn from a population of any given distribution with parameters $\mu$ and $\sigma$ will also be a normal distribution (variance is the averaged square of deviations from the mean values). The standard deviation of the limit distribution is described by the formula (Smirnow and Dunin-Barkowski 1973, p. 237):

$$\begin{aligned} \sigma _{S^{2}} =\sqrt{\frac{\mu _4 -\sigma ^{4}}{n}-\frac{2\cdot \left( {\mu _4 -2\cdot \sigma ^{4}} \right)}{n^{2}}+\frac{\mu _4 -3\cdot \sigma ^{4}}{n^{3}}}, \end{aligned}$$

(16)

where: $\mu _{4 }$ is the fourth central moment of variable $X.$

To determine the limit distribution of the unbiased estimator of variance $\hat{{S}}^{2}$ described by (11), we should correct the parameters of limit distributions, bearing in mind the relationship:

$$\begin{aligned} \hat{{S}}^{2}=\frac{n}{n-1}S^{2}. \end{aligned}$$

(17)

The expected value and standard deviation of estimator $\hat{{S}}^{2}$ is obtained through multiplying the parameters of the distribution estimator $S^{2}$ by $\frac{n}{n-1}$.

By using the exact bootstrap method the distribution of random variable $X$ is approximated by the distribution of discrete random variable $X^{D}$ with a realization set ($x_{1}, x_{2}, {\ldots }, x_{k})$ and probability distribution denoted by values $p_{i }= \text{ P}(X^{D}=x_{i})$, for $i= 1, {\ldots }, k$, whereby $\sum \nolimits _{i=1}^k {p_i } =1$. The expected value $\mu ^{D}$, standard deviation ${\sigma ^\mathrm{D}}$ and fourth central moment $\mu _4^\mathrm{D}$ of variable $X^{D}$ are equal, respectively:

$$\begin{aligned} \mu ^\mathrm{D}=\sum _{i=1}^k {x_i \cdot p{ }_i,}\quad \sigma ^\mathrm{D}=\sqrt{\sum _{i=1}^k {\left( {x_i -\mu ^\mathrm{D}} \right)^{2}\cdot p{ }_i} },\quad \mu _4^\mathrm{D} =\sum _{i=1}^k {\left( {x_i -\mu ^\mathrm{D}} \right)^{4}\cdot p{ }_i}.\nonumber \\ \end{aligned}$$

(18)

The normal limit distribution of estimator $\bar{{X}}$ will be denoted by GA and is as follows:

$$\begin{aligned} \text{ GA} \text{:} \text{ N}\left( {\mu ^{\mathrm{D}},{\sigma ^{\mathrm{D}}}/{\sqrt{n}}} \right). \end{aligned}$$

(19)

The limit distribution of estimator $\hat{{S}}^{2}$ will be denoted by GV (Smirnow and Dunin-Barkowski 1973, p. 237):

$$\begin{aligned}&\text{ GV:} \text{ N}\nonumber \\&\left( {\left( {\sigma ^{\mathrm{D}}} \right)^{2},\frac{n}{n-1}\sqrt{\frac{\mu _4^\mathrm{D} -\left( {\sigma ^{\mathrm{D}}} \right)^{4}}{n}-\frac{2\cdot \left( {\mu _4^\mathrm{D} -2\cdot \left( {\sigma ^{\mathrm{D}}} \right)^{4}} \right)}{n^{2}}+\frac{\mu _4^\mathrm{D} -3\cdot \left( {\sigma ^{\mathrm{D}}} \right)^{4}}{n^{3}}}} \,\right).\nonumber \\ \end{aligned}$$

(20)

4 A comparison of the exact and basic bootstrap

The basic bootstrap method is based on resampling the original sample, which may be interpreted as random sampling of the $B$ realization of an estimator of any given parameter. Arithmetic mean is calculated (according to formula 2) based on the randomly selected realizations. From all the BE resamples, $B$ samples may be selected in $BE^{B }$ ways. Even if BE is not large, $BE^{B }$ will be a very large number, which makes it impossible to calculate mean distribution. However, because $B$ is large, limit distribution may be used, which is normal distribution:

$$\begin{aligned} \text{ GO:N}\left( {\mu ^{\mathrm{BE}},\frac{\sigma ^{\mathrm{BE}}}{\sqrt{B}}} \right), \end{aligned}$$

(21)

where: $\mu ^{BE}$ and $\sigma ^{BE}$ are mean and standard deviation of the estimator of the parameter calculated using the exact bootstrap. This distribution allows for calculating the probability that estimating the parameter using basic bootstrap is within any given interval (in particular this may be confidence interval).

5 Results

5.1 Example 1

Suppose an $n$ element sample drawn from a unspecified probability distribution $F$ and represented by discrete random variable $X^{D}$ is given. The probability distribution $\hat{{F}}$ of $X^{D}$ is presented in Table 1. The expected value and standard deviation of $X^{D}$ equal $\mu ^{D} = 5.174$, and $\sigma ^{D} = 1.997429$, respectively.

Table 1 Distribution of random variable $X^{D}$

Two alternatives of the distributions of mean and variance estimators calculated using the exact bootstrap method and limit distributions are provided. The first one assumes that $n = 20$ and the second one $n= 30$. The samples were generated according to the algorithm proposed by (Fisher and Hall 1991).

5.1.1 Mean estimation for $n = 20$ and $n = 30$

In Fig. 1 there is the mean estimator distribution calculated using the exact bootstrap method (DBA) and the limit distribution GA defined by (19) in the interval separated from the mean by 4 standard deviations. The bootstrap distribution for the mean was provided as the probability of using individual values. In the case of the limit distributions, however, it is the probability of assuming the values of the interval (from the center of the interval between the values on the left to the center on the right). Both when $n = 30$ and $n = 20$ the diagrams are nearly identical. The probability values overlap with an accuracy to three decimal places.

In Table 2 there are parameters (mean and standard deviation) of the distribution estimators of the mean DBA and GA and the confidence intervals calculated using them. With regard to the parameters of the distributions they are nearly identical (with an accuracy to five decimal places for both sizes). In the case of the confidence intervals there are some differences. For $n = 20$ the interval boundaries of the confidence distributions DVA and GA differ in the second decimal place and for $n = 30$ in the third decimal place. We should stress that for the set sample size $n$ it is impossible to achieve an arbitrarily high accuracy of estimation as the exact bootstrap method DBA is a discrete distribution.

Fig. 1

Distributions of the GA and DBA mean estimators

Table 2 Confidence intervals of the mean computed using the exact DBA bootstrap method and the GA limit distribution

Comparing basic bootstrap with exact bootstrap allows for distribution as given by formula (21). In the case of mean the distribution will be $\text{ N}\left( {\mu ^\mathrm{D},\frac{\sigma ^\mathrm{D}}{\sqrt{n}\cdot \sqrt{B}}} \right)$. Assuming $B=1{,}000$ for $n=20$ we obtain $N$(5.174, 0.0141), and for $n=30$ the distribution will be $N$(5.174, 0.0115). Knowing the distribution we may calculate probability of the mean being estimated with the desired accuracy based on 1,000 resamples. In Table 3 there are probabilities for accuracies that equal 0.1, 0.01, 0.001 and 0.0001. The probability of estimation equals 1 only for the 0.1 accuracy and is $>$0.5 for the 0.01 accuracy. We may note that if we increase the requirements concerning the accuracy of estimation, the probability of fulfilling the requirements rapidly decreases, despite the large sample—1,000 elements. In such situations the exact bootstrap should be used, which guarantees no bias at the resampling stage.

Table 3 Probability that the mean calculated based on 1,000 bootstrap samples will be computed with the given accuracy

5.1.2 Variance estimation for $n = 20$ and $n = 30$

In Table 4 there are distributions of variance estimator determined using the exact bootstrap method (DBV) and limit distribution GV defined by formula (20). The number of different realizations of the variance estimator is significantly higher than that of the mean estimator. Therefore the probabilities for intervals rather than for individual values are shown in the table. If one should use them to calculate the parameters of the distributions in the same way as for grouped data; thus, the results may differ from the exact values.

The method of selecting the width of the intervals also requires some comment. For the limit (continuous) distributions and for each arbitrarily small interval the probability that the random variable will assume the values of this interval is $>$0. For the discrete distribution, and such is the variance estimator distribution calculated using the exact bootstrap method, the case is different. The smaller the interval width, the greater the number of intervals where the probability is equal to 0.

Moreover, in Table 4 the expected values of variance estimator distributions and their standard deviations are presented. These are exact values calculated based on all the generated realizations.

The expected values of limit distribution GV are equal to sample variance. In the case of the DBV distribution the expected value was also equal to the variance, which attests to the accuracy of the applied algorithm. The exact bootstrap method does not introduce additional estimator bias (contrary to the bootstrap method with random sampling).

Also, note that the standard deviation of the DBV distribution is equal to the standard deviation of the GV distribution with an accuracy to five decimal places.

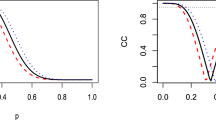
In Fig. 2 there is the distribution of the variance estimators for $n=20$ and $n=30$. They prove that the distribution GV constitute the correct approximation of the distribution DBV for the random variable whose distribution is presented in Table 1.

We should also note that the DBV distribution is slightly asymmetric in comparison to limit distributions. The difference is very small and the consistency of the GV and DBV distributions was confirmed by Pearson’s goodness of fit test, both for $n=20$ and $n=30$.

Fig. 2

Distributions of GV and DBV variance estimator

Table 4 Distributions of variance estimator: obtained using the exact DBV bootstrap method and limit distributions of variance estimator GV

Table 5 Confidence intervals of the variance constructed using the exact bootstrap method DBV and GV limit distributions

In Table 5 there are confidence intervals of the variance when using the exact bootstrap method (the DBV distribution) and the limit distribution GV.

Comparing the width of the intervals we can state that the more precise estimation was done using the exact bootstrap method (and it is an exact estimation), then the limit distribution GV (with the exception of $n=20$ and $1-\alpha = 0.99$, for which the confidence interval of the GV distribution was narrower than DVB).

The left shift of the intervals for the GV distribution in relation to DBV results from the asymmetry of the latter. The presented calculations indicate that the GV distribution is a good approximation of the DBV distribution.

Table 6 Probability that the variance calculated based on 1,000 bootstrap samples will be computed with the given accuracy

A comparison of the basic and exact bootstrap methods, as is the case with the mean, would allow for distribution given by formula (21). The distribution of estimator variance obtained by formula (21) will be

$$\begin{aligned} \text{ N}\left( {\left( {\sigma ^\mathrm{D}} \right)^{2},\frac{1}{\sqrt{B}}\cdot \frac{n}{n-1}}{\sqrt{\frac{\mu _4^\mathrm{D} -\left( {\sigma ^\mathrm{D}} \right)^{4}}{n}{-}\frac{2\cdot \left( {\mu _4^\mathrm{D} {-}2\cdot \left( {\sigma ^\mathrm{D}} \right)^{4}} \right)}{n^{2}}{+}\frac{\mu _4^\mathrm{D} -3\cdot \left( {\sigma ^\mathrm{D}} \right)^{4}}{n^{3}}}} \right). \end{aligned}$$

If $B=1{,}000$ for $n=20$ we obtain the distribution $N$(3.9897, 0.0290), and for $n=30$ the distribution is $N$(3.9897, 0.0233). In Table 6 there are probabilities of the mean being estimated based on 1,000 resamples with accuracy that equals 0.1, 0.01, 0.001 and 0.0001. The probability of obtaining 0.1 accuracy equals 1 for both sizes of the original sample. However, the 0.01 accuracy may be obtained with probability 0.2695 for $n=20$ and 0.3323 for $n=30$. For the accuracies 0.001 and 0.0001 the probabilities are very small. This is an indication of the need to use the exact bootstrap method in the case of estimating variance if the accuracy requirements are higher.

5.2 Example 2

The second simulation experiment for a small sample including the values {1, 2, 3, 4, 5}, assuming the same probabilities of random sampling of each element equal 0,2. This distribution is represented by discrete random variable $X^{D}$ with the expected value and variance equal to $\mu ^{D}= 3$, and $\left( {\sigma ^\mathrm{D}} \right)^{2}= 2$, respectively. Mean estimation for $n$ = 5.

The expected value of the mean estimator equals 3 and standard deviation is 0.6325 (according to formula (12)). From 5 elements of the original sample we may draw $5^{5}=3{,}125$ resamples. The probability of drawing each of them is the same in the given conditions and equals 1/3,125. Since the mean estimator for many resamples has the same values, the set of all it realizations includes only 21 realizations. Figure 3 shows the distribution of estimator probability calculated using the exact bootstrap method (denoted as DVA), and limit distribution GA denoted by formula (19). The probability of distributions DBA and GA is very large (the probabilities are equal with accuracy to two decimal places) even though the sample is small. The parameters of both distributions are identical, which is proved by the accuracy of the algorithm used.

Fig. 3

Distributions of the GA and DBA mean estimators for a small sample

Table 7 presents the probabilities that the mean based on 1,000 bootstrap samples will be calculated with a given accuracy. The probability was calculated based on limit distribution, which for $B=1{,}000$ is $N$(3, 0.0200). Only for the 0.1 accuracy does the probability equal 1. In all other cases the use of the exact bootstrap method is recommended.

Table 7 Probability that the mean computed based on 1,000 bootstrap small samples will be calculated with the given accuracy

5.2.1 Variance estimation for $n = 5$

The expected value of the unbiased variance estimator equals 2 and its standard deviation 0.9798 (according to formula (8) after correction of the factor 5/4). The variance estimator for the original sample has only 26 different values. Figure 4 presents the distribution of unbiased variance estimator calculated using the exact bootstrap method DBV. Normal limit distribution DV was included for comparison. The differences between the distributions are notable and we should state that in the case of a variance estimator for a small sample limit distribution should not be used.

Fig. 4

Distributions of the GV and DBV mean estimators for a small sample

Table 8 Probability that the variance calculated based on 1,000 bootstrap small samples will be computed with the given accuracy

Table 8 presents the probability that the variance calculated based on 1,000 bootstrap samples will be computed with the given accuracy. The probabilities were calculated using limit distribution $N$(2, 0.0310). As was the case with the mean, only for the 0.1 accuracy is the probability close to 1. In all other cases the use of the exact bootstrap method is recommended, since the probability of exact variance estimation using the basic bootstrap method is small.

6 Conclusion

In the article the exact bootstrap method was discussed. This method can be used to estimate the parameters of the estimators of random variables with an unknown distribution. The method allows for determining the estimation of an arbitrary parameter, the error of this estimation, the distribution estimator or confidence intervals. Traditionally, this problem is solved using the bootstrap method, which consists on resampling of the original random sample. Random sampling is used in statistics if the entire population can not be examined or the study would be too problematic. First of all, the original sample is finite, and secondly, its distribution is known – it is the empirical distribution. Instead of resampling, one can generate an entire space of resamples and determinate all the realizations of the statistic which is the estimator of the unknown parameter.

The method was used to estimate mean and variance. It was shown that the expected values of the estimators are equal to the mean and variance of the sample. The method, therefore, does not introduce bias resulting from resampling as it may occur in classical bootstrap.

The estimators distributions calculated using the exact bootstrap method was compared with the limit distributions. The similarity between the distributions indicates that there is a possibility of approximation of the “exact” distribution by the limit distribution if the sample is not too small.

In order to assess the effectiveness of the traditional bootstrap method, limit distribution of the mean calculated from $B$ realizations of the estimator of a given parameter (every realization is calculated based on a single bootstrap sample) was used. This distribution allows for calculating the probability of obtaining the assumed accuracy of estimation. Although the number of bootstrap resamples was large ($B=1{,}000$), both the mean and variance probabilities rapidly decreased as required accuracy increased. This proves that it is worth using the exact method, which guarantees that there will not additional bias at the resampling stage.

The conducted simulation experiments have revealed that in the case of small samples ($n\le 15$ and $k=n$) the time necessary to generate the entire space of resamples is short ($<$10 s using an average-quality computer). This means that there is no need for resampling. For larger samples, the time is much longer and requires several hours of computation (for $n=20$ and $k=n$ the calculations lasted 5 h and 30 min). The increase in size of the sample causes significant lengthening of the computation time. On the other hand, we should remember that the bootstrap method is used for small samples—for larger samples the limit distribution of estimators may be used. However, considering the progress in computer technology, the exact bootstrap method will also be used for lager samples in the future.

What are the consequences of the possibility of generating complete information contained in the sample as presented in the article? The fundamental issue is the much greater flexibility in constructing estimators as there is no need to make the assumption of the distribution form so that determining the distribution of the estimator would be possible. One should attempt to make the estimator unbiased, consistent and effective. The exact bootstrap method may also be useful in this matter.

Drawing a random sample may be seen as the replacement of a continuous random variable with an unknown distribution by a discrete variable with known distribution—the bootstrap distribution. Transformations of discrete variables are easier than transformations of continuous variables since the distribution of discrete variable statistics can be calculated automatically. In reality, due to the finite accuracy of all measurements we can only observe discrete variables. We may suppose that with the increasing power of computers their role in statistics will also increase.