On the choice of a noninformative prior for Bayesian inference of discretized normal observations

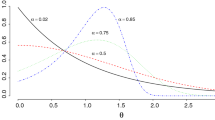
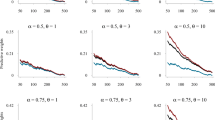
Abstract

We consider the task of Bayesian inference of the mean of normal observations when the available data have been discretized and when no prior knowledge about the mean and the variance exists. An application is presented which illustrates that the discretization of the data should not be ignored when their variability is of the order of the discretization step. We show that the standard (noninformative) prior for location-scale family distributions is no longer appropriate. We work out the reference prior of Berger and Bernardo, which leads to different and more reasonable results. However, for this prior the posterior also shows some non-desirable properties. We argue that this is due to the inherent difficulty of the considered problem, which also affects other methods of inference. We therefore complement our analysis by an empirical Bayes approach. While such proceeding overcomes the disadvantages of the standard and reference priors and appears to provide a reasonable inference, it may raise conceptual concerns. We conclude that it is difficult to provide a widely accepted prior for the considered problem.