Skip to main content
SpringerLink
Log in

Proposition for a Volumetric Error Model Considering Backlash in Machine Tools

  • Original Article
  • Published:
The International Journal of Advanced Manufacturing Technology Aims and scope Submit manuscript

Abstract

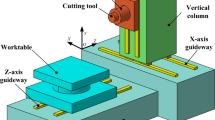
This paper proposes a new scheme for evaluating the machine tool volumetric error model including the backlash error. The effects of backlash errors are assessed by experiments, conducted on a three-axis vertical-type machining centre. The assessment was taken for 18 error components out of the 21 geometric errors of a machine tool. It was shown that the backlash error of a machine tool is one of the systematic errors. Some important characteristics of the backlash error were identified; that is, the backlash error is a function of position, it decreases as the feedrate increases, and its size and shape vary according to the machine structure.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. J. A. Soons, F. C. Theuws and P. H. Schellekens, “Modeling the errors of multi-axis machines: a general methodology”, Precision Engineering, 14(1), pp. 5–19, 1992.

    Article  Google Scholar 

  2. T. Treib, “Error budgeting-applied to the calculation and optimization of the volumetric error field of multiaxis systems”, Annals CIRP, 36(1), pp. 365–368, 1987.

    Article  Google Scholar 

  3. K. F. Eman and B. T. Wu, “A generalized geometric error model for multi-axis machines”, Annals CIRP, 36(1), pp. 253–256, 1987.

    Article  Google Scholar 

  4. J. Mou and C. R. Liu, “A method for enhancing the accuracy of CNC machine tools for on-machine inspection”, Journal of Manufacturing Systems, 11(4), pp. 229–237, 1992.

    Article  Google Scholar 

  5. Y. C. Shin and Y. Wei, “A statistical analysis of positional errors of a multiaxis machine tool”, Precision Engineering, 14(3), pp. 139–146, 1992.

    Article  Google Scholar 

  6. P. M. Fereira and C. R. Liu, “A method of estimating and compensating quasistatic errors of machine tools”, Transactions ASME, Journal of Engineering for Industry, 115, pp. 149–159, February 1993.

    Article  Google Scholar 

  7. U. Dorndorf, V. S. B. Kiridena and P. M. Ferreira, “Optimal budgeting of quasistatic machine tool errors”, Transactions ASME, Journal of Engineering for Industry, 116, pp. 42–53, February 1994.

    Article  Google Scholar 

  8. Y. C. Shin, H. Chin and M. J. Brink, “Characterization of CNC machining centers”, Journal of Manufacturing Systems, 10(5), pp. 407–421, 1991.

    Article  Google Scholar 

  9. V. B. Kreng, C. R. Jiu and C. N. Chu, “A kinematic model for machine tool accuracy characterisation”, The International Journal of Advanced Manufacturing Technology, 9, pp. 79–86, 1994.

    Article  Google Scholar 

  10. J. Mou and C. R. Liu, “A methodology for machine tools error corretion using reference parts”, International Journal of Computer Integrated Manufacturing, 8(1), pp. 64–77, 1995.

    Article  Google Scholar 

  11. S. Sartori and G. X. Zhang, “Geometric error measurement and compensation of machines”, Annals CIRP, 44(2), pp. 599–609, 1995.

    Article  Google Scholar 

  12. Y. Shen and N. A. Duffie, “An uncertainty analysis method for coordinate referencing in manufacturing systems”, Transactions ASME, Journal of Engineering for Industry, 117, pp. 42–48, February 1995.

    Article  Google Scholar 

  13. X. B. Chen, A. Geddam and Z. J. Yuan, “Accuracy improvement of three-axis CNC machining centers for quasi-static error compensation”, Journal of Manufacturing Systems, 16(5), pp. 323–336, 1997.

    Article  Google Scholar 

  14. S. Chatterjee, “An assessment of quasi-static and operational errors in NC machine tools”, Journal of Manufacturing Systems, 16(1), pp. 59–68, 1997.

    Article  Google Scholar 

  15. Alexander H. Slocum, Precision Machine Design, Prentice-Hall, Englewood, Cliffs, NJ, 1992.

    Google Scholar 

  16. Manfred Weck, Handbook of Machine Tools, Volume 4: Metrological Analysis and Performance Tests (translated into English by H. Bibring), John Wiley, 1984.

    Google Scholar 

  17. Layton C. Hale and Alexander H. Slocum, “Design of antibacklash transmissions for precision position control systems”, Precision Engineering, 16(4), pp. 244–258, 1994.

    Article  Google Scholar 

  18. Manfred Weck, Handbook of Machine Tools, Volume 3: Automation and Controls (translated into English by H. Bibring), John Wiley, 1984.

    Google Scholar 

  19. E. S. Lee, “Computer aided volumetric error calibration of CNCmachine and coordinate measuring machine by the artifact method”, PhD thesis, University of Manchester, 1993.

    Google Scholar 

  20. K. J. Bathe, Finite Element Procedures in Engineering Analysis, Prentice Hall, Englewood Cliffs, NJ, 1982.

    Google Scholar 

  21. H. J. Pahk, “Computer aided volumetric error calibration of coordinate measuring machine”, PhD thesis, University of Manchester, 1990.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Pohang University of Science and Technology, Pohang, South Korea

    Kyoung Gee Ahn & Dong Woo Cho

Authors
  1. Kyoung Gee Ahn
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Dong Woo Cho
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Ahn, K., Cho, D. Proposition for a Volumetric Error Model Considering Backlash in Machine Tools. Int J Adv Manuf Technol 15, 554–561 (1999). https://doi.org/10.1007/s001700050101

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s001700050101

Key words

Search

Navigation