Skip to main content
SpringerLink
Log in

Effect of complicated deformation behaviors during cold stamping on springback prediction of DP980 steel

  • ORIGINAL ARTICLE
  • Published:
The International Journal of Advanced Manufacturing Technology Aims and scope Submit manuscript

Abstract

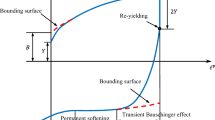
High-strength DP980 steel has been used on the automobile to improve the crash safety and lightweight, but serious springback is unavoidable during stamping. In this paper, complicated deformation behaviors during cold stamping of DP980 steel are investigated by combining experiment and simulation in order to promote the accuracy of springback prediction. Deformation behaviors including varied elasticity, anisotropic yield, and cyclic hardening are studied by testing, modelling, and model-programming. Firstly, uniaxial tension, biaxial tension, and in-plane cyclic tension–compression tests are carried out by a self-developed platform to test the mechanical behaviors of DP980 steel in the complicated deformation process. Secondly, elastic, yield, and hardening behaviors are modelled and evaluated. A modified elastic attenuation model by establishing a relation between chord elastic modulus and plastic strain is proposed to describe the elastic behavior. Three yield models, such as BBC2005, Hill-1948, and von-Mises, are presented to compare the description ability to the yield locus and anisotropy. A coupled isotropic and nonlinear kinematic (CINK) hardening model is proposed to accurately describe the hardening behaviors (Bauschinger effect, transient effect and permanent softening) by cyclic tension and compression loads. Finally, U-shaped part is stamped and simulated by using models that can describe actual deformation behaviors. The springback prediction with modified elastic attenuation, anisotropic yield, and CINK hardening models obtains an optimal result, and the overall relative error is only 1.803%. Among three factors, the effect of elastic attenuation on springback is the greatest. The results show that the accurate testing, modelling, and implementing of complicated deformation behaviors of DP980 steel contribute to high-precision simulation results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21

Similar content being viewed by others

Data availability

All data have been included in this article.

References

  1. Cao J, Banu M (2020) Opportunities and challenges in metal forming for lightweighting: review and future work. J Manuf Sci Eng Trans ASME 142:1–24. https://doi.org/10.1115/1.4047732

    Article  Google Scholar 

  2. Lim H, Lee MG, Sung JH, Kim JH, Wagoner RH (2012) Time-dependent springback of advanced high strength steels. Int J Plast 29:42–59. https://doi.org/10.1016/j.ijplas.2011.07.008

    Article  Google Scholar 

  3. Grilo TJ, Valente RAF, Alves de Sousa RJ (2015) Modelling non-quadratic anisotropic yield criteria and mixed isotropic-nonlinear kinematic hardening: analysis of forward- and backward-Euler formulations. Int J Mater Form 8:533–547. https://doi.org/10.1007/s12289-014-1176-9

    Article  Google Scholar 

  4. Lee J, Lee J-Y, Barlat F, Wagoner RH, Chung K, Lee M-G (2013) Extension of quasi-plastic–elastic approach to incorporate complex plastic flow behavior – application to springback of advanced high-strength steels. Int J Plast 45:140–159. https://doi.org/10.1016/j.ijplas.2013.01.011

    Article  Google Scholar 

  5. Zang SL, Lee MG, Sun L, Kim JH (2014) Measurement of the Bauschinger behavior of sheet metals by three-point bending springback test with pre-strained strips. Int J Plast 59:84–107. https://doi.org/10.1016/j.ijplas.2014.03.015

    Article  Google Scholar 

  6. Geng L, Wagoner, RH (2000) Springback Analysis with a Modified Hardening Model. SAE 2000 Transactions 109:365–375. https://doi.org/10.4271/2000-01-0768

  7. Choi J, Lee J, Bong HJ, Lee M-G, Barlat F (2017) Advanced constitutive modeling of advanced high strength steel sheets for springback prediction after double stage U-draw bending. Int J Solids Struct 151:152–164. https://doi.org/10.1016/j.ijsolstr.2017.09.030

    Article  Google Scholar 

  8. Ziegler H (1959) A modification of Prager’s hardening rule. Q Appl Math 17:55–65. https://doi.org/10.1090/qam/104405

    Article  MathSciNet  MATH  Google Scholar 

  9. Chaboche JL (1986) Time-independent constitutive theories for cyclic plasticity. Int J Plast 2:149–188. https://doi.org/10.1016/0749-6419(86)90010-0

    Article  MATH  Google Scholar 

  10. Cao J, Lee W, Cheng HS, Seniw M, Wang HP, Chung K (2009) Experimental and numerical investigation of combined isotropic-kinematic hardening behavior of sheet metals. Int J Plast 25:942–972. https://doi.org/10.1016/j.ijplas.2008.04.007

    Article  MATH  Google Scholar 

  11. Zang SL, Guo C, Thuillier S, Lee MG (2011) A model of one-surface cyclic plasticity and its application to springback prediction. Int J Mech Sci 53:425–435. https://doi.org/10.1016/j.ijmecsci.2011.03.005

    Article  Google Scholar 

  12. Yoshida F, Uemori T (2002) A model of large-strain cyclic plasticity describing the Bauschinger effect and workhardening stagnation. Int J Plast 18:661–686. https://doi.org/10.1016/S0749-6419(01)00050-X

    Article  MATH  Google Scholar 

  13. Ghaei A, Green DE, Taherizadeh A (2010) Semi-implicit numerical integration of Yoshida-Uemori two-surface plasticity model. Int J Mech Sci 52:531–540. https://doi.org/10.1016/j.ijmecsci.2009.11.018

    Article  Google Scholar 

  14. Zhang C, Lou Y, Clausmeyer T, Tekkaya AE (2021) Cyclic loading tests based on the in-plane torsion test for sheet metal. In: Daehn G, Cao J, Kinsey B et al (eds) Forming the Future. Springer International Publishing, Cham, pp 635–645

    Chapter  Google Scholar 

  15. Fincato R, Tsutsumi S, Zilio A, Mazzucco G, Salomoni V (2021) Fully implicit numerical integration of the Yoshida-Uemori two-surface plasticity model with isotropic hardening stagnation. Frat ed Integrità Strutt 15:114–126. https://doi.org/10.3221/IGF-ESIS.57.10

    Article  Google Scholar 

  16. Barlat F, Yoon SY, Lee SY, Wi MS, Kim JH (2020) Distortional plasticity framework with application to advanced high strength steel. Int J Solids Struct 202:947–962. https://doi.org/10.1016/j.ijsolstr.2020.05.014

    Article  Google Scholar 

  17. Barlat F, Gracio JJ, Lee MG, Rauch EF, Vincze G (2011) An alternative to kinematic hardening in classical plasticity. Int J Plast 27:1309–1327. https://doi.org/10.1016/j.ijplas.2011.03.003

    Article  MATH  Google Scholar 

  18. He J, Han G, Guo C (2021) Non-associated anisotropic plasticity of metal sheets based on the distortional concept. Thin-Walled Struct 161. https://doi.org/10.1016/j.tws.2021.107523

  19. Choi H, Choi S, Kang SC, Kim C, Lee MG (2021) Prediction of anisotropic strengths of steel plate after prior bending-reverse bending deformation: application of distortional hardening model. Int J Mech Sci 204:106512. https://doi.org/10.1016/j.ijmecsci.2021.106512

  20. Lee SY, Kim JM, Kim JH, Barlat F (2020) Validation of homogeneous anisotropic hardening model using non-linear strain path experiments. Int J Mech Sci 183. https://doi.org/10.1016/j.ijmecsci.2020.105769

  21. He J, Han G, Li S, Zou D (2019) To correlate the phase transformation and mechanical behavior of QP steel sheets. Int J Mech Sci 152:198–210. https://doi.org/10.1016/j.ijmecsci.2019.01.003

    Article  Google Scholar 

  22. Lee EH, Choi H, Stoughton TB, Yoon JW (2019) Combined anisotropic and distortion hardening to describe directional response with Bauschinger effect. Int J Plast 122:73–88. https://doi.org/10.1016/j.ijplas.2019.07.007

    Article  Google Scholar 

  23. Banabic D (2010) Sheet metal forming processes. Springer Berlin Heidelberg, Berlin, Heidelberg

    Book  Google Scholar 

  24. Hill R (1948) A theory of the yielding and plastic flow of anisotropic metals. Proc R Soc London Ser A Math Phys Sci 193:281–297. https://doi.org/10.1098/rspa.1948.0045

    Article  MathSciNet  MATH  Google Scholar 

  25. Barlat F, Brem JC, Yoon JW, Chung K, Dick RE, Lege DJ, Pourboghrat F, Choi SH, Chu E (2003) Plane stress yield function for aluminum alloy sheets — part 1: theory. Int J Plast 19:1297–1319. https://doi.org/10.1016/S0749-6419(02)00019-0

    Article  MATH  Google Scholar 

  26. Barlat F, Yoon JW, Cazacu O (2007) On linear transformations of stress tensors for the description of plastic anisotropy. Int J Plast 23:876–896. https://doi.org/10.1016/j.ijplas.2006.10.001

    Article  MATH  Google Scholar 

  27. Banabic D, Aretz H, Comsa DS, Paraianu L (2005) An improved analytical description of orthotropy in metallic sheets. Int J Plast 21:493–512. https://doi.org/10.1016/j.ijplas.2004.04.003

    Article  MATH  Google Scholar 

  28. Comsa D, Banabic D (2008) Plane-stress yield criterion for highly-anisotropic sheet metals. Numisheet 2008 0:43–48

  29. Xu Y, Zeng XC, Tian YQ, Xia LL, Zhang SH, Li YL (2021) Experimental study on anisotropy of mechanical properties of coldrolled dual-phase steel sheet. J Plast Eng 28:124–130

    Google Scholar 

  30. Li XQ, Dong HR, Yu CW, Wang HB, Yang YF, Song BY, Wan Z, Li DH (2020) Influence of yield criteria and hardening model on draw-bending springback prediction of DP780. J Mech Eng 56:42–55. https://doi.org/10.3901/JME.2020.12.042

    Article  Google Scholar 

  31. Uemori T, Sumikawa S, Naka T, Ma N, Yoshida F (2017) Innuence of Bauschinger effect and anisotropy on springback of aluminum alloy sheets. Mater Trans 58:921–926. https://doi.org/10.2320/matertrans.L-M2017812

    Article  Google Scholar 

  32. Chongthairungruang B, Uthaisangsuk V, Suranuntchai S, Jirathearanat S (2013) Springback prediction in sheet metal forming of high strength steels. Mater Des 50:253–266. https://doi.org/10.1016/j.matdes.2013.02.060

    Article  Google Scholar 

  33. Toros S, Polat A, Ozturk F (2012) Formability and springback characterization of TRIP800 advanced high strength steel. Mater Des 41:298–305. https://doi.org/10.1016/j.matdes.2012.05.006

    Article  Google Scholar 

  34. Liao J, Xue X, Lee MG, Barlat F, Gracio J (2014) On twist springback prediction of asymmetric tube in rotary draw bending with different constitutive models. Int J Mech Sci 89:311–322. https://doi.org/10.1016/j.ijmecsci.2014.09.016

    Article  Google Scholar 

  35. Kim H, Kim C, Barlat F, Pavlina E, Lee MG (2013) Nonlinear elastic behaviors of low and high strength steels in unloading and reloading. Mater Sci Eng A 562:161–171. https://doi.org/10.1016/j.msea.2012.11.020

    Article  Google Scholar 

  36. Chen Y, Li X, Lang L (2019) Various elastic moduli of AA6016 and their application on accurate prediction of springback. J Chinese Inst Eng Trans Chinese Inst Eng A 42:319–326. https://doi.org/10.1080/02533839.2019.1584765

    Article  Google Scholar 

  37. Choi Y, Lee J, Panicker SS, Jin HK, Panda SK, Lee MG (2020) Mechanical properties, springback, and formability of W-temper and peak aged 7075 aluminum alloy sheets: experiments and modeling. Int J Mech Sci 170. https://doi.org/10.1016/j.ijmecsci.2019.105344

  38. Lee JY, Lee MG, Barlat F, Chung KH, Kim DJ (2016) Effect of nonlinear multi-axial elasticity and anisotropic plasticity on quasi-static dent properties of automotive steel sheets. Int J Solids Struct 87:254–266. https://doi.org/10.1016/j.ijsolstr.2016.01.020

    Article  Google Scholar 

  39. Chen Z, Gandhi U, Lee J, Wagoner RH (2016) Variation and consistency of Young’s modulus in steel. J Mater Process Technol 227:227–243. https://doi.org/10.1016/j.jmatprotec.2015.08.024

    Article  Google Scholar 

  40. Morestin F, Boivin M (1996) On the necessity of taking into account the variation in the Young modulus with plastic strain in elastic-plastic software. Nucl Eng Des 162:107–116. https://doi.org/10.1016/0029-5493(95)01123-4

    Article  Google Scholar 

  41. Yoshida F, Uemori T, Fujiwara K (2002) Elastic-plastic behavior of steel sheets under in-plane cyclic tension-compression at large strain. Int J Plast 18:633–659. https://doi.org/10.1016/S0749-6419(01)00049-3

    Article  MATH  Google Scholar 

  42. Sun L, Wagoner RH (2011) Complex unloading behavior: nature of the deformation and its consistent constitutive representation. Int J Plast 27:1126–1144. https://doi.org/10.1016/j.ijplas.2010.12.003

    Article  MATH  Google Scholar 

  43. Cleveland RM, Ghosh AK (2002) Inelastic effects on springback in metals. Int J Plast 18:769–785. https://doi.org/10.1016/S0749-6419(01)00054-7

    Article  MATH  Google Scholar 

  44. Chang Y, Wang N, Wang BT, Li XD, Wang CY, Zhao KM, Dong H (2021) Prediction of bending springback of the medium-Mn steel considering elastic modulus attenuation. J Manuf Process 67:345–355. https://doi.org/10.1016/j.jmapro.2021.04.074

    Article  Google Scholar 

  45. Yoshida F, Amaishi T (2020) Model for description of nonlinear unloading-reloading stress-strain response with special reference to plastic-strain dependent chord modulus. Int J Plast 130:102708. https://doi.org/10.1016/j.ijplas.2020.102708

  46. Deng N, Kuwabara T, Korkolis YP (2015) Cruciform specimen design and verification for constitutive identification of anisotropic sheets. Exp Mech 55:1005–1022. https://doi.org/10.1007/s11340-015-9999-y

    Article  Google Scholar 

  47. Lee KJ, Lee MG (2019) Pressure and sliding velocity dependent surface asperity based friction model: application to springback simulation. IOP Conf Ser Mater Sci Eng 651:0–6. https://doi.org/10.1088/1757-899X/651/1/012079

  48. Wagner L, Wallner M, Larour P, Steineder K, Schneider R (2021) Reduction of Young’s modulus for a wide range of steel sheet materials and its effect during springback simulation. IOP Conf Ser Mater Sci Eng 1157:012031. https://doi.org/10.1088/1757-899x/1157/1/012031

  49. Lee JY, Lee JW, Lee MG, Barlat F (2012) An application of homogeneous anisotropic hardening to springback prediction in pre-strained U-draw/bending. Int J Solids Struct 49:3562–3572. https://doi.org/10.1016/j.ijsolstr.2012.03.042

    Article  Google Scholar 

  50. Choi JH, Zang SL, Lee MG, Kim JH, Barlat F (2019) Determining the coefficients of a homogeneous anisotropic hardening model for ultrathin steel sheets. Int J Mech Sci 157–158:428–438. https://doi.org/10.1016/j.ijmecsci.2019.04.050

    Article  Google Scholar 

Download references

Funding

This work was supported by the National Natural Science Foundation of China (51971050), Open Project of State Key Laboratory of Advanced Special Steel and Shanghai Key Laboratory of Advanced Ferrometallurgy of Shanghai University (SKLASS 2020–01), and the Science and Technology Commission of Shanghai Municipality (19DZ2270200).

Author information

Authors and Affiliations

  1. School of Automotive Engineering, Dalian University of Technology, No.2 Linggong Rd., Ganjingzi Dist., Dalian, 116024, China

    Baotang Wang, Ying Chang, Xiaodong Li & Shuzhou Yu

  2. State Key Laboratory of Advanced Special Steel and Shanghai Key Laboratory of Advanced Ferrometallurgy, Shanghai University, Shanghai, 200444, China

    Ying Chang

  3. School of Mechanical Engineering, Xi’an Jiaotong University, Xi’an, 710049, China

    Shunlai Zang

  4. Central Iron & Steel Research Institute (CISRI), Beijing, 100081, China

    Cunyu Wang

Authors
  1. Baotang Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ying Chang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Shunlai Zang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Xiaodong Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Shuzhou Yu
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Cunyu Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

BaoTang Wang: conceptualization, methodology, investigation, experiment and simulation, and writing—original draft; Ying Chang: conceptualization, methodology, writing—review and editing, funding acquisition, and supervision; Shunlai Zang: conceptualization, writing—review and editing; XiaoDong Li: conceptualization, result analysis, and writing—review and editing; Shuzhou Yu: experiment; CunYu Wang: methodology and experiment.

Corresponding author

Correspondence to Ying Chang.

Ethics declarations

Ethics approval

This article does not contain any studies with human participants or animals performed by any of the authors.

Consent to participate

The authors agree to the authorship order.

Consent for publication

All authors have read and agreed to the published version of the manuscript.

Competing interests

The authors declare no competing interests.

Additional information

Publisher's note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, B., Chang, Y., Zang, S. et al. Effect of complicated deformation behaviors during cold stamping on springback prediction of DP980 steel. Int J Adv Manuf Technol 126, 4997–5015 (2023). https://doi.org/10.1007/s00170-023-11453-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00170-023-11453-7

Keywords

Search

Navigation