Skip to main content
SpringerLink
Log in

The central strain analytical modeling and analysis for the plate rolling process

  • ORIGINAL ARTICLE
  • Published:
The International Journal of Advanced Manufacturing Technology Aims and scope Submit manuscript

Abstract

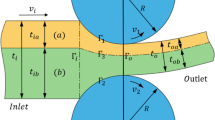
The strain after rolling plays an important role in the prediction of the microstructure and properties and plate deformation permeability. So, it is necessary to establish a more accurate theoretical strain model for the rolling process. This paper studies the modeling method of the equivalent strain based on the upper bound principle and the stream function method. The rolling deformation region is divided into three zones (inlet rigid zone, plastic zone, and outlet rigid zone) according to the kinematics. The boundary conditions of adjacent deformation zones are modified according to the characteristics of each deformation zone. A near-real kinematics admissible velocity field is established by the stream function method on this basis. The geometric boundary conditions of the deformation region are obtained. The deformation power, friction power, and velocity discontinuous power are calculated according to the redefined geometric boundary conditions. On this basis, the generalized shear strain rate intensity is calculated according to the minimum energy principle. Finally, the equivalent strain model after rolling is obtained by integrating the generalized shear strain rate in time. The plate rolling experiments of AA1060 and the numerical simulations are carried out with different rolling reductions to verify the analytic model precision of the equivalent strain. The results show that the minimum and the maximum relative equivalent strain deviation between the analytic model and the experiment is 0.52% and 9.96%, respectively. The numerical calculation and experimental results show that the model can accurately calculate the strain along the plate thickness. This model can provide an important reference for the rolling process setup and the microstructure and properties prediction.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Data availability

Data and materials will be available upon request.

Abbreviations

H :

Initial plate thickness

h :

Plate thickness after rolling

Δh :

Reduction

L :

Length of the deformation region

Г 1, Г 2 :

Velocity discontinuities

R :

Radius of the top and bottom work rolls

Φ :

Flow in the unit section

x n 1 :

Neutral point

l :

Length of deformation region

ω :

Speed of work rolls

θ :

Feed angle

γ :

Neutral angle

y 1(x):

Geometric equation of rolling contact arc

y 2(x):

Geometric equation of Г1

y 3(x):

Geometric equation of Г2

σ s :

Yield strength

k :

Shear yield strength

M :

Friction coefficient

x, y :

Cartesian coordinates

a, b :

Correction factor of the streamline

α :

The angle between the tangent of velocity discontinuity (Г1) and horizontal direction

β :

The angle between the tangent of velocity discontinuity (Г2) and horizontal direction

v 0 :

Inlet velocity

v 1 :

Outlet velocity

v x :

Horizontal velocity component

v y :

Vertical velocity component

\(\dot{\varepsilon }_{x}\) :

Strain rate along the x direction

\(\dot{\varepsilon }_{y}\) :

Strain rate along the y direction

W :

Total power

W V :

Power consumed in deformation region

W f :

Power with the friction by the work roll

W Г 1 :

Power consumed in inlet velocity discontinuities

W Г 2 :

Power consumed in outlet velocity discontinuities

Λ:

Cumulative shear strain strength

\(\dot{\Gamma }\) :

Generalized shear strain rate intensity

References

  1. Pan H, Cheng R, Du S, Xie H, Qin G (2020) Achieving high strength in micro-alloyed Mg-Al-Ca-Zn-Mn-Ce alloy sheet processed by single-pass large-strain rolling. J Mater Eng Perform 29(3):1–10. https://doi.org/10.1007/s11665-020-05188-9

    Article  Google Scholar 

  2. Zhang T, Wu YX, Gong H, Zheng XZ, Jiang SS (2014) Effects of rolling parameters of snake hot rolling on strain distribution of aluminum alloy 7075. T Nonferr Metal Soc 24(7):2150–2156. https://doi.org/10.1016/S1003-6326(14)63326-4

    Article  Google Scholar 

  3. Jiang LY, Zhao CJ, Shi JH, Yuan G, Wang XQ, Huang QX (2015) Hot rolled strip re-reddening temperature changing law during ultra-fast cooling. J Iron Steel Res Int 220(008):694–702. https://doi.org/10.1016/S1006-706X(15)30059-5

    Article  Google Scholar 

  4. Hacquin A, Montmitonnet P, Guillerault JP (1996) A steady state thermo-elastoviscoplastic finite element model of rolling with coupled thermo-elastic roll deformation. J Mater Process Technol 60(1):109–116. https://doi.org/10.1016/0924-0136(96)02315-1

    Article  MATH  Google Scholar 

  5. Hsiang SH, Lin SL (2001) Application of 3D FEM-slab method to shape rolling. Int J Mech Sci 43(5):1155–1177. https://doi.org/10.1016/S0020-7403(00)00064-3

    Article  MATH  Google Scholar 

  6. Pustovoytov D, Pesin A, Biryukova O (2018) Finite element analysis of strain gradients in aluminum alloy sheets processed by asymmetric rolling. Procedia Manufacturing 15:129–136. https://doi.org/10.1016/j.promfg.2018.07.186

    Article  Google Scholar 

  7. Bian S, Zhang XA, Li S, Zhang LA, Li W, Yan LB (2020) Numerical Simulation, Microstructure, properties of EH40 ultra-heavy plate under gradient temperature rolling. Mater Sci and Eng A. https://doi.org/10.1016/j.msea.2020.139778

    Article  Google Scholar 

  8. Schmidtchen M, Kawalla R (2016) Fast numerical simulation of symmetric flat rolling processes for inhomogeneous materials using a layer model − part I: basic theory. Steel Res Int 87(8):1065–1081. https://doi.org/10.1002/srin.201600047

    Article  Google Scholar 

  9. Jiang LY, Zhen T, Yuan G, Huang JB, Wei YY, Li H, Wang P (2020) The mechanical parameters modeling of heavy steel plate snake/gradient temperature rolling with the same roll diameters. Metall Res Technol 117(3):301. https://doi.org/10.1051/metal/2020019

    Article  Google Scholar 

  10. Zhao DW, Zhang SH, Li CM, Song HY, Wang GD (2012) Rolling with simplified stream function velocity and strain rate vector inner product. J Iron Steel Res Int 19(003):20–24. https://doi.org/10.1016/S1006-706X(12)60068-5

    Article  Google Scholar 

  11. Zhang SH, Song BN, Gao SW, Guan M, Zhou J, Chen XD, Zhao DW (2018) Upper bound analysis of a shape-dependent criterion for closing central rectangular defects during hot rolling. Appl Math Model 55:674–684. https://doi.org/10.1016/j.apm.2017.11.012

    Article  MATH  Google Scholar 

  12. Oh SI, Kobayashi S (1975) An approximate method for a three-dimensional analysis of rolling. Int J of Mech Sci 17(4):293–305. https://doi.org/10.1016/0020-7403(75)90010-7

    Article  MATH  Google Scholar 

  13. Bayoumi Laila S (1998) Flow and stresses in round–oval–round roll pass sequence. Int J Mech Sci 40(12):1223–1234. https://doi.org/10.1016/S0020-7403(98)00005-8

    Article  MATH  Google Scholar 

  14. Wang JP, Lin YT (1995) The load analysis of the plane-strain forging processes using the upper-bound stream-function elemental technique. J Mater Process Tech 47(3–4):345–359. https://doi.org/10.1016/0924-0136(95)85008-2

    Article  Google Scholar 

  15. Maity KP, Kar PK, Das NS (1996) A class of upper-bound solutions for the extrusion of square shapes from square billets through curved dies. J Mater Process Tech 62(1–3):185–190. https://doi.org/10.1016/0924-0136(95)02228-7

    Article  Google Scholar 

  16. Aksakal B, Sezek S, Can Y (2005) Forging of polygonal discs using the dual stream functions. Mater Design 26(8):643–654. https://doi.org/10.1016/j.matdes.2004.09.005

    Article  Google Scholar 

  17. Hwang YM, Hsu HH, Lee HJ (1995) Analysis of sandwich sheet rolling by stream function method. Int J Mech Sci 39(3):598–605. https://doi.org/10.1016/0020-7403(95)93522-8

    Article  MATH  Google Scholar 

  18. Hwang YM, Hsu HH (1998) Analysis of plate rolling using the dual-stream function method and cylindrical coordinates. Int J Mech Sci 40(4):371–385. https://doi.org/10.1016/S0020-7403(97)00040-4

    Article  MATH  Google Scholar 

  19. Sezek S, Aksakal B, Can Y (2008) Analysis of cold and hot plate rolling using dual stream functions. Mater Design 29(3):584–596. https://doi.org/10.1016/j.matdes.2007.03.005

    Article  Google Scholar 

  20. Ali Nuri Doğruoğlu (2001) On constructing kinematically admissible velocity fields in cold sheet rolling. J Mater Process Tech 110(3):287–299. https://doi.org/10.1016/S0924-0136(00)00897-9

    Article  Google Scholar 

  21. Liu YM, Zhang DH, Zhao DW, Sun J (2016) Analysis of vertical rolling using double parabolic model and stream function velocity field. Int J Adv Manuf Technol 82(5–8):1153–1161. https://doi.org/10.1007/s00170-015-7393-7

    Article  Google Scholar 

Download references

Funding

The authors gratefully appreciate the financial support by the National Natural Science Foundation of China under Grant 51804206, the Major Science and Technology Projects in Shanxi under Grant 20181102016.

Author information

Authors and Affiliations

  1. School of Mechanical Engineering, Taiyuan University of Science and Technology, Taiyuan, 030024, People’s Republic of China

    Lian-Yun Jiang, Yao-Yu Wei, Heng Li & Li-feng Ma

Authors
  1. Lian-Yun Jiang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yao-Yu Wei
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Heng Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Li-feng Ma
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

LJ: conceptualization; writing—original draft preparation; visualization; project administration. YW: writing—original draft preparation; visualization. HL: writing—review and editing; supervision. LM: writing—review and editing, supervision.

Corresponding author

Correspondence to Yao-Yu Wei.

Ethics declarations

Ethical approval

Not applicable.

Consent to participate

Not applicable.

Consent for publication

Not applicable.

Conflict of interest

The authors declare no competing interests.

Additional information

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jiang, LY., Wei, YY., Li, H. et al. The central strain analytical modeling and analysis for the plate rolling process. Int J Adv Manuf Technol 118, 2873–2882 (2022). https://doi.org/10.1007/s00170-021-08148-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00170-021-08148-2

Keywords

Search

Navigation