Skip to main content
SpringerLink
Log in

Thermal simulation speculation-based active coolant control onto spindle bearings

  • ORIGINAL ARTICLE
  • Published:
The International Journal of Advanced Manufacturing Technology Aims and scope Submit manuscript

Abstract

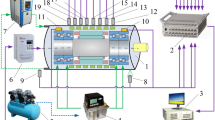
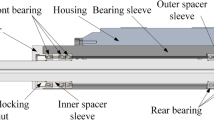
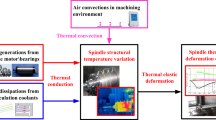
For thermal perception and control onto spindle bearings without spindle/bearing structural modifications for built-in thermal sensors, this paper proposes a thermal simulation speculation-based active coolant control strategy onto spindle bearings, for spindle accuracy guarantee. Firstly, numerical simulation technology is adopted to construct thermal collection of spindle bearings influenced by coolants. Secondly, this collection is utilized as the basis for ELM speculation modeling for bearing thermal behaviors. Eventually, the previous active coolant strategy is modified to be equipped with the model above for the speculation perception (according to the detectable spindle working parameters) and active control realization onto thermal behaviors of spindle bearings. It is verified by experiment and simulation that the thermal simulation speculation-based active coolant strategy is more advantageous than the previous strategy, in thermal stabilization and accuracy guarantee of motorized spindle unit. Besides, the power ratio between coolant heat dissipation and bearing heat generation is suggested to be 1.15:1 for a sufficient thermal balance of spindle bearings, which brings the design guidance onto cooling capacity/strategy of recirculation cooling equipment for motorized spindle unit.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

Availability of data and material

Data generated or analyzed in this study are available.

Abbreviations

ρ oil_sol /ρ oil :

Density of coolant oil or solid/density of coolant oil (kg/m3)

k oil_sol :

Thermal conductivity of coolant oil or solid (W/(m·K))

H en :

Energy content per unit mass (J)

p :

Pressure (Pa)

\( \overrightarrow{v} \)/\( \overset{=}{\tau } \) :

Velocity vector/stress tensor

S h :

Heat generation power of volumetric heat source (W)

u/ v/ w :

Coolant flowing velocity on X/Y/Z direction (m/s)

\( \nabla \bullet \left(\overset{=}{\tau}\overrightarrow{v}\right) \) :

Viscous power dissipation of flowing coolant (W)

∇ • (k ∇ T):

Heat transfer among solid, flowing coolant, and ambient air (W)

Φ b/Φ m :

Heat generation power of spindle bearing/motor (W)

n :

Spindle rotating speed (RPM)

M 0/M 1 :

Bearing frictional torque caused by bearing lubricant viscosity/applied force (Nmm)

f 0/f 1 :

Factor related to the type, structure, force, and lubrication of bearings

ν 0 :

Kinematics viscosity of lubricant (mm2/s)

F β :

Applied force load onto bearing (N)

D m :

Mean diameter of bearing (mm)

P h/P CU/P f :

Power of motor magnet/electric/mechanical loss (W)

C :

Constant value related to electrical steel grades

f :

Magnetizing frequency (s−1)

B max :

Maximum magnetic flux density (T)

t :

Thickness of silicon steel sheet (m)

ρ/ρ air/ρ coo :

Density of iron core/air/coolant (kg/m3)

γ c :

Resistivity of iron core (Ω)

I :

Current (A)

ρ C :

Resistivity of a conductor (Ω)

L :

Length of a conductor (m)

S :

Sectional area of a conductor (m2)

C ′ :

Frictional coefficient

R f/L f :

Outer radius/length of rotor (m)

ω :

Angular velocity of rotor (rad/s)

h f/n :

Coefficient of forced/natural convection heat transfer (W/(m2K))

Nu :

Nusselt number

λ :

Thermal conductivity of air (W/(m·K))

d e/l e :

Diameter/length of spindle part (m)

Re/Pr:

Reynolds number/Prandtl number of air

u air :

Flow velocity of air (m/s)

ν air :

Kinematics viscosity of air (m2/s)

P 1–4 :

Design variables 1–4 for optimization

Te/Ts :

Experimental/simulated temperature data of motorized spindle unit (°C)

T coo _ fbg(bb)/T out _ fbg(bb) :

Coolant supply/output temperature for spindle front bearing group (back bearing) (°C)

T ssb _ fbg(bb) :

Spindle shell temperature nearby front bearing group (back bearing) (°C)

T fbg(bb) :

Temperature of spindle front bearing group (back bearing) (°C)

a r/b r :

Learning parameters of SLFN rth hidden nodes

β r :

SLFN rth output weight

x :

Input vector for SLFN

G(a r, b r, x):

Activation function denoting output of rth hidden nodes ar/br with respect to input x

t :

SLFN output variable

L :

Number of SLFN hidden nodes

M :

Number of spindle thermal simulations in collection

N :

Moment number of each spindle transient thermal simulation

c coo :

Coolant special heat (J/(kg·K))

Q coo :

Coolant supply volume rate (L/min)

Φ coo :

Coolant heat dissipation (W)

References

  1. Liu T, Gao WG, Zhang DW, Zhang YF, Chang WF, Liang CM (2017) Analytical modeling for thermal errors of motorized spindle unit. Int J Mach Tools Manuf 112:53–70

    Article  Google Scholar 

  2. Chou C, DeBra DB (1990) Liquid temperature control for precision tools. CIRP Ann Manuf Technol 39:535–543

    Article  Google Scholar 

  3. Abele E, Altintas Y, Brecher C (2010) Machine tool spindle units. CIRP Ann Manuf Technol 59:781–802

    Article  Google Scholar 

  4. Cao HR, Zhang XW, Chen XF (2017) The concept and progress of intelligent spindles: a review. Int J Mach Tools Manuf 112:21–52

    Article  Google Scholar 

  5. Creighton E, Honegger A, Tulsian A, Mukhopadhyay D (2010) Analysis of thermal errors in a high-speed micro-milling spindle. Int J Mach Tools Manuf 50(4):386–393

    Article  Google Scholar 

  6. Han J, Wang LP, Yu LQ (2010) Modeling and estimating thermal error in precision machine spindles. Appl Mech Mater 34:507–511

    Article  Google Scholar 

  7. Holkup T, Cao H, Kolar P, Altintas Y, Zeleny J (2010) Thermo-mechanical model of spindles. CIRP Ann Manuf Technol 59(1):365–368

    Article  Google Scholar 

  8. Li DX, Feng PF, Zhang JF, Wu ZJ, Yu DW (2014) Calculation method of convective heat transfer coefficients for thermal simulation of a spindle system based on RBF neural network. Int J Adv Manuf Technol 70(5):1445–1454

    Article  Google Scholar 

  9. Chen DJ, Bonis M, Zhang FH, Dong S (2010) Thermal error of a hydrostatic spindle. Precis Eng 35(3):512–520

    Article  Google Scholar 

  10. Su H, Lu LH, Liang YC, Zhang Q, Sun YZ (2014) Thermal analysis of the hydrostatic spindle system by finite volume element method. Int J Adv Manuf Technol 71(9):1949–1959

    Article  Google Scholar 

  11. Liu ZF, Pan MH, Zhang AP, Zhao YS, Yang Y, Ma CY (2015) Thermal characteristic analysis of high-speed motorized spindle system based on thermal contact resistance and thermal-conduction resistance. Int J Adv Manuf Technol 76(9):1913–1926

    Article  Google Scholar 

  12. Zivkovic A, Zeljkovic M, Tabakovic S, Milojevic Z (2015) Mathematical modeling and experimental testing of high-speed spindle behavior. Int J Adv Manuf Technol 77(5):1071–1086

    Article  Google Scholar 

  13. Lee J, Kim DH, Lee CM (2015) A study on the thermal characteristics and experiments of high-speed spindle for machine tools. Int J Precis Eng Manuf 16(2):293–299

    Article  Google Scholar 

  14. Ma C, Yang J, Zhao L, Mei XS, Shi H (2015) Simulation and experimental study on the thermally induced deformations of high-speed spindle system. Appl Therm Eng 86:251–268

    Article  Google Scholar 

  15. Huang JH, Than VT, Ngo TT, Wang CC (2016) An inverse method for estimating heat sources in a high speed spindle. Appl Therm Eng 105:65–76

    Article  Google Scholar 

  16. Zheng DX, Chen WF, Li MM (2018) An optimized thermal network model to estimate thermal performances on a pair of angular contact ball bearings under oil-air lubrication. Appl Therm Eng 131:328–339

    Article  Google Scholar 

  17. Liu T, Gao WG, Tian YL, Zhang HJ, Chang WF, Mao K, Zhang DW (2015) A differentiated multi-loops bath recirculation system for precision machine tools. Appl Therm Eng 76c:54–63

    Article  Google Scholar 

  18. Liu T, Gao WG, Tian YL, Zhang DW, Zhang YF, Chang WF (2017) Power matching based dissipation strategy onto spindle heat generations. Appl Therm Eng 113:499–507

    Article  Google Scholar 

  19. Zhang YF, Wang P, Liu T, Gao WG, Chang WF, Tian YL, Zhang DW (2018) Active and intelligent control onto thermal behaviors of a motorized spindle unit. Int J Adv Manuf Technol 98:3133–3146

    Article  Google Scholar 

  20. Anderson JD (1995) Computational fluid dynamics: the basics with applications. McGraw Hill, New York

    Google Scholar 

  21. Jorgensen BR, Shin YC (1997) Dynamics of machine tool spindle/bearing systems under thermal growth. J Tribol 119(4):875–882

    Article  Google Scholar 

  22. López de Lacalle LN, Lamikiz A (2009) Machine tools for high performance machining. Springer, London

  23. Xu M, Jiang SY, Cai Y (2007) An improved thermal model for machine tool bearings. Int J Mach Tools Manuf 47(1):53–62

    Article  Google Scholar 

  24. Huang GB, Zhu QY, Siew CK (2006) Extreme learning machine: theory and applications. Neurocomputing 70(1–3):489–501

    Article  Google Scholar 

  25. Parkus H (1976) Thermoelasticity. Springer, Vienna

  26. ISO 230-3-2007. Test code for machine tools - Part 3: Determination of thermal effects (Second Edition)

Download references

Acknowledgments

The authors acknowledge the Fund of National Nature Science Foundation of China (No. 51775375), Fund of Nature Science Foundation in Tianjin of China (No. 17JCZDJC40300), and Open Fund of Jiangsu Key Laboratory of Precision and Micro-Manufacturing Technology.

Funding

The research was supported by the Fund of National Nature Science Foundation of China (No. 51775375), Fund of Nature Science Foundation in Tianjin of China (No. 17JCZDJC40300), and Open Fund of Jiangsu Key Laboratory of Precision and Micro-Manufacturing Technology.

Author information

Authors and Affiliations

  1. School of Mechanical Engineering, Hebei University of Technology, Tianjin, 300130, China

    Teng Liu, Liang Zhou & Jianjun Zhang

  2. Key Laboratory of Mechanism Theory and Equipment Design of Ministry of Education, Tianjin University, Tianjin, 300355, China

    Teng Liu, Weiguo Gao, Wenfen Chang & Dawei Zhang

  3. School of Computer Science and Technology, Civil Aviation University of China, Tianjin, 300300, China

    Yifan Zhang

  4. Beijing Precision Machinery& Engineering Research Co., Ltd., Beijing, 101312, China

    Wenfen Chang

Authors
  1. Teng Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Liang Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Weiguo Gao
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Yifan Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Wenfen Chang
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Jianjun Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Dawei Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Teng Liu is the main contributor to this paper. He finished the thermal simulation modeling of motorized spindle unit and then corrected its thermal loads by optimization method. The aim is to construct the thermal collection of spindle bearings influenced by coolants. Furthermore, he performed the contrasting experiments for this study and finished the handwriting of the manuscript as a whole.

Liang Zhou finished ELM-based speculation modeling for bearing thermal behaviors, and the previous active coolant strategy is then modified by him to be equipped with the ELM model.

Weiguo Gao gave Teng Liu the significant guidance about the thermal simulation modeling method of motorized spindle unit and finished the construction of experimental platform.

Yifan Zhang finished the data analyses about the experimental and simulation results.

Wenfen Chang provided this study with the test platform of motorized spindle unit and gave some valuable suggestions onto the experimental method.

Jianjun Zhang designed the logical structure of the whole manuscript.

Dawei Zhang gave crucial comments onto this work for improving its technical route.

Corresponding author

Correspondence to Teng Liu.

Ethics declarations

Competing interests

The authors declare that they have no competing interests.

Ethical approval

Not applicable.

Consent to participate

All authors consent to participate in the author team of this submitted manuscript.

Consent to publish

The submitted manuscript is approved by all its authors for publication.

Additional information

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, T., Zhou, L., Gao, W. et al. Thermal simulation speculation-based active coolant control onto spindle bearings. Int J Adv Manuf Technol 113, 337–350 (2021). https://doi.org/10.1007/s00170-021-06613-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00170-021-06613-6

Keywords

Search

Navigation