Non-uniform crystallinity and temperature distribution during adjacent laser-assisted tape winding process of carbon/PA12 pipes

Abstract

The non-uniform temperature and crystallinity distributions present in carbon fiber–reinforced PA12 composite pipes, produced via laser-assisted tape winding (LATW), are investigated in this paper. The width of the laser source is usually larger than the substrate width which causes multiple heating and cooling of some regions of the (neighboring) substrate and hence temperature and crystallinity gradients during the adjacent hoop winding. A kinematic-optical-thermal (KOT) model coupled with a non-isothermal crystallinity model is developed to capture the transient temperature and crystallinity distributions for growing substrate thickness and width. The predicted temperature trends are validated with thermocouple and thermal camera measurements. The substrate temperature varies in the width direction up to 52%. This will lead to extra polymer remelting and possible degradation. The maximum variation of the crystallinity degree across the width is found to be 270% which shows agreement with the trend of the measured crystallinity degree. It is found that a more realistic description of the melting behavior of the matrix is needed to obtain a more accurate prediction of the crystallinity distribution.

Nomenclature

c p	Specific heat capacity	(J kg ∘C− 1)
h	Heat transfer convection coefficient	(W m− 2 ∘C− 1)
k	Thermal conductivity	(W m− 1 ∘C− 1)
K G	Growth rate constant	(K2)
K 0	Nucleation rate constant	(s− 1)
m f	Mass fraction of the fiber reinforcement	(-)
n	Refractive index, Avrami exponent	(-)
$q^{\prime \prime }$	Absorbed heat flux	(W m− 2)
R	Universal gas constant	(J mol− 1 K− 1)
R s	Substrate radius	(m)
t	Time	(s)
t p	Thickness of prepreg	(m)
t 1/2	Isothermal crystallization half time	(s)
T	Temperature	(K)
TCC	Thermal contact conductance coefficient	(W m− 2 ∘C− 1)
$T_{g}, T_{m}, T_{\infty }$	Glass transition, melting, and Vogel temperatures	(∘C)
U	Activation energy for crystallization	(J mol− 1)
v	Winding velocity or tape feeding rate	(m s− 1)
V f	Volume fraction of the fiber reinforcement	(-)
w p	Width of prepreg	(m)
x, y, z	Spatial coordinates	(m)
𝜃	Winding angle	(∘)
κ	Crystallization rate constant	(s− 1)
ξ	Relative degree of crystallinity	(-)
ρ	Density	(kg m− 3)
ϕ 0	Relative crystallized volume for 3D spherulitic growth without impingement	(-)
$\chi _{v(\infty )}$	Crystallized volume (in equilibrium condition)	(m3)
${\Delta } H_{f}^{\circ }$	Heat of fusion of 100% crystalline polymer at the equilibrium melting temperature	(J g− 1)
${\Delta } H_{f}^{\circ }$	Integrated melting enthalpy during heating process	(J g− 1)

1 Introduction

There is a growing need for several kilometers long continuous pipes for offshore oil and gas applications such as risers, used to convey hydrocarbons from unexploited reserves to the main land. Since the structure should be self-supporting, the heavy weight is a challenge in terms of mechanical performance [1]. Continuous fiber-reinforced polymer (FRP) composites are a suitable alternative for traditional metals due to the high specific strength, and corrosion and fatigue resistance [2,3,4]. Moreover, thermoplastic composites avoid the post-process step for curing in an autoclave which is a barrier for manufacturing such long structures with thermoset composites.

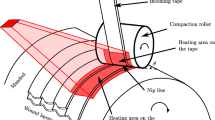
Automated tape winding (ATW) is one of the state-of-the-art processes to manufacture thermoplastic tubular structures such as the mentioned pipes and risers [1]. These tubular composite products are built layer by layer onto a mandrel or liner in the ATW processes. The prepreg tape and the laid down substrate are locally molten by a heat source before coming into contact at the nip point which can be seen schematically in Fig. 1a. To achieve the desired processing temperature at the nip line, it is very important to preheat the tape and substrate surfaces because the material is advected or the heat input is transported toward the bonding region with the tape feeding rate. The heat source in ATW processes can be a hot gas torch [5], infrared lamp [6, 7], or, recently, near-infrared (NIR) diode lasers better known as laser-assisted tape winding (LATW) [8,9,10,11,12]. In case of the adjacent hoop winding process which is used to manufacture thermoplastic pipes as seen in Fig. 1b, tapes are wound adjacently with a consistent winding angle forming one layer, and the following layer is manufactured with a different winding angle. This process is repeated until the desired composite layup is reached. In situ consolidation, which is the main mechanism to form the final product, takes place at the nip point where the melted incoming tape and substrate bond due to pressure applied by a compaction roller. The consolidation process includes several highly temperature-dependent steps such as the development of intimate contact followed by the healing of the polymeric matrix, which was studied for the automated fiber placement (AFP) and laser-assisted tape placement (LATP) processes in [13,14,15,16,17,18]. The inter-molecular diffusion or healing phenomenon describes the entanglement of polymer chains from one surface to the opposite one. Therefore, for a proper healing at the interfaces, the polymer needs to be melted to some extent in the depth of the tape and substrate [19]. The absorbed heat at the illuminated surfaces is mainly dissipated in the thickness direction due to the heat sink behavior of the roller and liner; therefore, the melting temperature can be easily achieved in the sufficient depth of the substrate and tape for a proper consolidation. There have been several studies to evaluate the in situ consolidation development during LATP of carbon-reinforced thermoplastics [14, 18, 20,21,22,23] and LATW of glass fiber/phenolic resin thermoset [16]. Also, the mechanical performance of the composite pipes was studied for various loading conditions [24,25,26]. The degree of crystallinity (DoC) is another temperature-dependent structural parameter which affects the mechanical performance of the crystalline FRP products [27,28,29,30,31,32]. The desired DoC depends on the application of the manufactured thermoplastic part. For the parts with a high interlaminar fracture toughness and large plastic deformation, a low level of DoC is required. Whereas for the parts with high tensile modulus and strength, a high DoC is desired [29, 32]. During the LATW process, multiple intensive heating and cooling cycles take place due to a localized heat input by the high-powered laser which affect the final DoC throughout the product. In the past, the non-uniform DoC distribution was predicted in the thickness direction for carbon fiber–reinforced PEEK (C/PEEK) laminates manufactured by the AFP process [33, 34].

Fig. 1

a Schematic view of the LATW process. Different substrate layers are denoted as sub-a to sub-d. b A photograph of the LATW setup and c and the operating units of the tape laying head

It has become clear that understanding and predicting the temperature evolution are key aspects in ensuring a proper consolidation and the manufacturing of high-quality parts. To illustrate this, a fitting example is found in the adjacent hoop winding studied here. Generally, the width of the laser spot is larger than the tape width to fully irradiate the incoming tape and substrate surfaces. As a consequence, some regions of the substrate layers contain extra heating and cooling cycles during adjacent placement of the incoming tape [6] leading to DoC variation across the tape width. To illustrate, the substrate layers sub-a, sub-c, and sub-d are also heated while winding the incoming tape on top of sub-b as indicated in Fig. 1a. The multiple heating and cooling of the adjacent layers can therefore cause non-uniform temperature and crystallinity distribution across the substrate width. Thus, the substrate temperature evolution together with the crystallinity behavior in the width direction needs to be measured and described properly. This is a challenging task in adjacent hoop winding and fiber placement processes because the growing-in-time thermal domain with adjacent paths needs to be considered in the process analysis.

Several studies have focused on monitoring the temperature during AFP or ATW processes where multiple tapes are deposited on top of each other [9, 11, 22, 35,36,37]. However, the critical analysis of the adjacent AFP/ATW process of fiber-reinforced polymer composites has received less attention in the literature. The temperature evolution during a continuous hoop filament winding process of thermoplastic composites, in which an infrared heat source was used, was measured and simulated in [7]. The temperature variation in the width direction was found to be negligible since the heat source width occupied one-third of the total mandrel length which provided a nearly uniform surface temperature distribution. In a second example, glass/polypropylene (G/PP) cylinders were manufactured using an automated hoop winding process using a hot gas torch in [5]. Two pyrometers were used to measure the tape and substrate temperatures just before the nip point. An almost-constant nip point temperature history was observed with a good agreement with the numerical predictions. The AFP process with adjacent placement paths was studied in [6]. The temperature evolution of prepreg slit-tape having a width of 3.2 mm was measured by using thermocouples. In addition to the experiments, a 1D finite difference (FD) model and a 3D finite element (FE) model were developed to predict the process temperature.

Considering the current literature, the temperature and crystallinity variations across the width of relatively wide substrate/tape have not been studied for the continuous laser-assisted adjacent hoop winding of thermoplastic composites. In this process, the multiple heating and cooling cycles of the substrate layers directly affect the temperature history of the material during manufacturing. The process temperature can eventually become higher than the thermal stability temperature of the material which may cause material degradation, even within a short time [38]. Therefore, the distribution and evolution of the substrate temperature have to be described and predicted properly in order to optimize the continuous LATW processes with adjacent paths. The objective of this work is to critically analyze the effect of multiple heating and cooling cycles on the temperature and crystallinity distributions during continuous LATW process with adjacent paths. To achieve this, a global kinematic-optical-thermal (KOT) model is developed. The 2D kinematic-thermal model is developed by means of an explicit finite difference method. The growing-in-time thermal domains are defined to capture the additive manufacturing of the deposited tape. A 3D optical model is used to estimate the anisotropic reflection of the laser rays which is coupled with the thermal model to provide the heat flux distribution as a surface boundary condition. The semi-crystalline PA12 was chosen for our investigation since the material is well available and currently gaining attention in the oil and gas industry [39]. During the manufacturing of C/PA12 pipes, the temperature distribution on the prepreg surfaces is measured by a thermal imaging camera. Thermocouples are used to capture the temperature evolution in the substrate due to multiple heating and cooling. The crystallinity distribution of the pipe cross section is investigated by employing a non-isothermal crystallinity model and also taking the melting kinetics into account. The predicted crystallinity distribution across the width is compared with the crystallinity of several cut-out sections of the manufactured pipe, obtained using differential scanning calorimetry (DSC).

2 Experimental

The continuous adjacent hoop winding experiments were performed by using the gantry-based laser-assisted tape placement system developed at Fraunhofer IPT. The main units are shown in Fig. 1c including the material storage, tape feed unit, cutting unit, consolidation unit with water-cooled consolidation roller and optional silicone sleeve, and the zoom-homogenization laser optics as the heating unit. The diode laser was an LDF1000-2500 by Laserline (max. laser power 2500 W, wavelengths 940 nm and 980 nm). The optical section consisted of a Zoom Homogenizer OTZ by Laserline. The prepreg material was a carbon fiber–reinforced polyamide-12 (PA12) from Evonik with a fiber volume fraction of V_f = 45% or mass fraction m_f = 55%. The thermoplastic liner was manufactured with a similar thermoplastic material, i.e., PA12, to ensure proper bonding of the first tape layer. The relative positions of the laser source, incoming tape, roller, and the substrate are depicted in Fig. 2. The reference values of the geometrical parameters in Fig. 2 are presented in Table 1 and were used in the KOT model. The constant tape feeding rate, i.e., linear winding velocity, laser power, consolidation force, and tape tension were v = 200 mm/s, P = 1650 W, 100 N, and 5 N, respectively. The laser source had a top-hat power distribution. A total of 3 composite parts were manufactured with a thickness of 5 layers and a length of 150 mm. Layers 1, 2, and 5 were wound on top of each other, while layers 3 and 4 were wound with an offset of half a tape width compared with layers 1 and 2, as schematically shown in Fig. 3.

Fig. 2

Schematic view of the geometry used for the optical model (reproduced with permission from [44])

Fig. 3

a A view of the thermocouple embedded in the substrate. The locations of the DSC samples extracted across the substrate width, i.e., from the left, center, and right zones. b The corresponding schematic view of the thermocouple location during winding of each layer which is shown separately for layers 1 to 4

Table 1 Reference values used in the LATW process

The trajectory of the tape on the liner was a helical path which defined the gap between the adjacent layers accordingly. To avoid possible overlaps at the tape edges, the helix pitch should be a bit larger than the as-received prepreg width since the tape width expands during the heating and consolidation phases [20, 40]. The tape laying head moved in lateral (x-) direction with a distance being equal to the tape width (w) for each full rotation. Hence, the winding angle was calculated based on the following equation [5]:

$$ \theta=\pm \arctan \left( \frac{2\pi R_{s}}{w_{p}} \right) $$

(1)

where the R_s was the substrate radius and w_p was the prepreg width. The corresponding stacking sequence of the cylinder wall layup was determined as [86.8/ − 86.8/86.8/ − 86.8/86.8] for R_s = 2.5 mm and w_p = 20 mm.

2.1 Temperature measurements

K-Type wire thermocouples of the Omega 5TC series with an accuracy of 1.5 ∘C were used to provide contact temperature measurement at the plies interfaces through the substrate thickness (Fig. 3a). The thermocouples were insulated with PFA (perfluoroalkoxy alkanes) tapes and had a diameter of 0.13 mm. The stripped leads of the thermocouples were connected to a Graphtec GL220 data logger capable of the simultaneous recording of 10 signals with a frequency of 10 Hz. In each trial, 3 thermocouples (TC1-TC3) were used to study the temperature distribution in thickness and width direction. After winding each layer, the whole system was stopped to install the thermocouples on the newly formed substrate. Therefore, the temperature of the system reached room temperature before winding of the next layer. The thermocouple tips were placed manually at 2 to 3 mm away from the tape edge in the width direction (x-direction); therefore, the exact positions was kept within a tolerance of a few millimeters during the manual installation. In terms of measurement location with respect to depositing tape width, the TC1 had an offset of half a tape as schematically demonstrated in Fig. 3b. When the thermocouples were positioned on the top surface of the substrate, e.g., TC1 during winding of layer 1 as seen in Fig. 3a, the temperature measurements may not be reliable because the laser light directly hits the thermocouple. This can lead to a significant temperature increase in the thermocouple which may not represent the actual substrate temperature. Therefore, the temperature evolution on the surface was captured by employing a thermal camera.

The thermal camera mounted on the tape winding head with a fixed distance of 326 mm to the nip point was a Pyroview 160L compact+ by DIAS Infrared. It exhibited a measurement frequency of 35 Hz, an image resolution of 160 × 120 pixels, and a maximum measurement deviation of 2%. The temperature obtained by this non-contact device was extracted by the software Pyrosoft Professional by DIAS Infrared assuming an emission coefficient of 0.9 and an ambient temperature of 20 ∘C based on previously performed calibrations. Characteristic temperature values for incoming tape, substrate, and nip point were evaluated as the average value in a rectangular box with a size of 6 × 3 pixels (tape/substrate) and 8 × 2 pixels (nip point), respectively. The tape and substrate boxes were located with a distance of approximately 15 mm from the nip point (see Fig. 4a).

Fig. 4

a A snapshot of the thermal imaging camera and the extraction of characteristic values from the infrared thermal imaging camera. The adjacent heating zones (4 mm) on the left and right hand sides of the heating zone are shown as strips in a. b Top-hat laser irradiation distribution along length and width of the deposited tape

2.2 DSC test for crystallization measurement

Differential scanning calorimetry (DSC) tests were performed with a TA Instruments Discovery 250. The samples were extracted across the substrate width of row 2 as shown in Fig. 3a for left, central, and right zones. Three trials of sample were extracted for repeat-ability purposes which makes 9 samples in total with an average mass of 9 mg each. The final crystallinity across the substrate width after winding of 5 layers was obtained by integrating the total melting enthalpy (compensating for any cold crystallization) upon a first heating cycle using the TA Trios software. The samples were heated from room temperature up to 210 ∘C with a heating rate of 10 ∘/min. The mass fraction of the fiber reinforcement (m_f) was subtracted from the total sample mass in order to correctly determine the crystallinity using [41]:

$$ \chi_{v} = \frac{\Delta H_{c}}{\Delta H_{f}^{\circ}\left( 1-m_{f}\right)} $$

(2)

where ${\Delta } H_{f}^{\circ }= {209.3}$ J g^− 1 [42, 43] was the heat of fusion of 100% crystalline neat PA12 at the equilibrium melting temperature, and ΔH_c was the integrated melting enthalpy during heating. Finally, a peak crystallization temperature of 151 ∘C was obtained by cooling the sample back to room temperature at 20 ∘C/min.

3 Kinematic-optical-thermal (KOT) model coupled with the crystallinity model

3.1 Optical model

The optical model was based on the work carried out by Reichardt et al. [44] in which a non-specular ray-tracing approach was utilized. The varying incident angle of the incoming rays due to the substrate and tape cylindrical curvature was considered in the model assuming a winding angle of 90∘. Moreover, the anisotropic reflection of the laser rays caused by the fibers was modelled to obtain the heat flux distribution. The optical model consisted of a macro-model launching a set of collimated rays from the laser position with uniform constant intensity across the width and length of the laser spot which did not consider the top-hat distribution as shown in Fig. 4b. The laser source was modeled with N₀ = 10,000 light rays from the laser position using Sobol sampling. In the optical macro-model, the location where each ray directly hit on the tape, substrate, or roller was calculated. The curved surfaces were approximated using a finite number of triangular mesh elements. The interactions between a specific coming ray and the tape or substrate geometry were described using the optical micro-model. The reflected and absorbed energy together with reflection directions were calculated at the material surface. The anisotropic reflection behavior of the composite surface was described using a bidirectional reflectance distribution function (BRDF). The reflected light was modeled by generating new rays which were forwarded to the macro-model. This iterative process was terminated after a set number of reflections defined by the user. The total number of reflections was set to 2 in the present study. Since the cylindrical liner was a single curved surface, the curved surface was unfolded and the heat flux distribution was demonstrated in the unfolded 2D Cartesian domain. To do so, the absorbed light was collected to the nearest square bins of 1 mm² where the incoming or reflected ray incident point fell in. The location of the bins in the winding direction was defined based on the arc-distance to the nip line. The output of the optical model was a 2D heat flux field $q^{\prime \prime }_{i}$ (laser power per unit area) applied to the substrate and tape surface. This information was then forwarded to the thermal model as a heat flux boundary condition to calculate the temperature distribution.

3.2 Heat transfer model

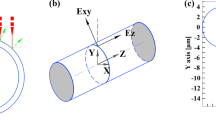
The substrate computational domain was defined as a cross-sectional slice of the substrate and liner with a Cartesian coordinate system as shown in Fig. 5. In this domain, the liner rotated and the tape laying head moved laterally along the centerline of the liner axis. Therefore, the computational domain was assumed to rotate with the liner and the thermal domain of the substrate was defined to grow both in thickness (z-direction) and width direction (x-direction). The tape temperature distribution was calculated with the same approach as the substrate domain. However, the incoming tape thickness and the corresponding thermal boundary conditions were assumed constant for all layers as also observed previously [5]. A schematic view of the 2D model in width and through-thickness directions is given in Fig. 6 together with the considered control volumes for the substrate and tape. The corresponding governing equation for the 2D transient heat conduction thermal domain is as follows [45]:

$$ \rho c_{p} \frac{\partial T}{\partial t} = \frac{\partial}{\partial x} \left( k_{x} \frac{\partial T} {\partial x} \right) + \frac{\partial}{\partial z} \left( k_{z} \frac{\partial T} {\partial z} \right) $$

(3)

where ρ, c_p, k_x, and k_z were the density, specific heat capacity, thermal conductivity in width, and through-thickness direction, respectively. The thermal properties of the used materials are listed in Table 2. The prepreg tape properties were considered temperature dependent. The density of the PA12 matrix was also a function of absolute crystallinity which was assumed constant (χ= 12%) in the process to avoid extra complexity to the model. The polymer conductivity depended on the the crystallization onset temperature which was also assumed constant (T_c = 162 ∘C). The conductivity and density of the prepreg were derived by the rule of mixture. The thermal degradation temperature of PA12 is determined at 350 ∘C [46]. The in-plane heat transfer rate due to conduction in the winding direction is much lower than the relative velocity of the laser source and heating surface [19]. It was therefore assumed that the in-plane heat conduction in winding direction was neglected in the present study. An explicit control volume-based finite difference (CV/FD) scheme [47] was used to solve Eq. 3. A relatively small time step was used (Δt ≈ 5 ms) to have a stable solution of the explicit solver. For each layer of the substrate and the incoming tape, 4 and 21 control volumes were defined in the thickness and width direction, respectively. A total of 5 control volumes were defined in the through-thickness direction for the liner having a thickness of 5 mm.

Fig. 5

Thermal model approach in width and thickness direction. v is the winding velocity and 𝜃 is the winding angle, i.e., the angle of velocity direction and liner axis

Fig. 6

A schematic view of the computational thermal model in width and thickness direction at the a heating region (t1–t2) and b consolidation (t2–t3) and cooling regions (t3–t1). Tape also had the same computational domain except that the liner was removed and instead convection boundary condition was applied as the roller heat loss effect

Table 2 Overview of prepreg and liner thermal properties. χ is the absolute crystallinity of the PA12 assumed 12% on average in this process. T_c = 162 ∘C is the crystallization onset temperature for PA12 [60, 61]

The substrate and tape computational domains were initially located at t = t1 (refer to Fig. 5), just at the beginning of the heated region and with an initial ambient temperature. As the substrate domain rotated in the same direction as the liner, the surface of the substrate (S1) and tape (S4) were irradiated by the laser and the heat fluxes were calculated by the optical model during t = t1 − t2 ($\scriptstyle -k\nabla T = \scriptstyle q^{\prime \prime }_{i}$). The corresponding computational domains in the heating region are illustrated in Fig. 6a. As explained in Fig. 1a, extra heating zones on the left and right sides of the substrate (S2 and S3 as seen in Fig. 5) were also heated in addition to the region where the incoming tape was deposited. The air convection boundary condition (−k∇T=h_a[T_surr−T(t)]) was defined on the surfaces S1 − S4, where h_a was the air heat transfer coefficient and T_surr was the surrounding (ambient) temperature. The heat transfer between the roller and tape was modeled as a convective boundary condition on the S5 surface (−k∇T=h_tr[T_roller−T(t)]) where h_tr was the heat transfer coefficient at the tape-roller interface and T_roller was the roller temperature. Since the roller was water-cooled, a lower value of T_roller = 25 ∘C was used compared to an air-cooled roller with a temperature of 50 ∘C [48].

The tape temperature was calculated in a separated domain (Fig. 6a) prior to the substrate to provide the tape temperature for the substrate at the nip point. At the nip point (t = t2), the substrate thermal domain grew in the thickness direction equal to the tape thickness (Fig. 6b). At the interface of the tape and the substrate at t = t2, the nodal temperatures was updated based on the averaged temperature of the tape and substrate. From t = t2 to t = t3, the consolidated substrate lost heat to the roller. The roller thermal effect was simulated by the convection heat loss on the S6 surface (−k∇T=h_r[T_roller−T(t)]) where h_r was the heat transfer coefficient at the substrate-roller interface. The length (C = 46 mm) and duration (C/v = 0.23 s) of the roller contact area depended on the roller indentation (I = 10 mm) into the liner surface (refer to Table 1).

Finally, the air convection heat loss was applied after t = t3 on the substrate top surface (S7) until the thermal domain reached the heating region again at t = t1. The liner was considered a physical body instead of a convection boundary condition for the substrate model. By this assumption, the heat loss distribution to the liner in the thickness and width direction was predicted with higher accuracy compared to convection heat loss. A thermal contact conductance between the liner and substrate was utilized with a value of TCC_m = 4000 W m^− 2∘C^− 1 which was in the range of the reported values in [49].

The coefficients needed for the explained boundary conditions and the domain mesh sizes are provided in Table 3. The mesh size variation in the thickness direction was considered in the formulation. In the model, a perfect bonding between the rest of the layers was assumed since thermal contact resistance between the layers is negligible [49].

Table 3 Overview of reference values for numerical parameters in the thermal simulation

3.3 Kinematic model

The kinematic model for the hoop winding process is schematically shown in Fig. 7 for adjacent winding of three tapes (rows 1, 2, and 3) in the x-direction with three layers (layers 1, 2, and 3) in the z-direction. The winding velocity was defined as a vector sum of the lateral tape laying head velocity and liner linear rotational velocity. The lateral velocity value was calculated as vcos𝜃 = 11.16 mm/s, and the linear rotational velocity was defined by vsin𝜃 = 199.69 mm/s as shown in Fig. 5. The duration for one full rotation of the liner is then $\frac {2\pi R_{s}}{vsin\theta } = {2}$s. The discussed time-dependent boundary condition on the top surface of substrate in the Section 3.2 was therefore directly dependent on the liner rotational velocity.

Fig. 7

Global numerical strategy of hoop winding for manufacturing a cylinder with a thickness of 5 layers and a width of 3 tapes. The deposition of the incoming tape is visualized at each 360∘ of winding in the growing computational model. Each figure represents the geometry of the computational domain for one full rotation. The schematics do not represent the actual size of computational domain

In Fig. 7, the growing computational thermal domain of the substrate is demonstrated during the process. At t = 2s, the deposition of the tape at row 1 is illustrated corresponding to the start of the process for each layer. At t = 4s, the next tape was placed adjacent to the first tape after one full rotation of the liner. Winding continued until the tape laying head reached the end of the pipe length. Then, the process stopped due to the thermocouple installation and the system reached the ambient temperature and then tape laying head started to wind the second layer as shown in Fig. 7. This process continued until all tapes were wound to reach the desired layup of the pipe which consisted of 5 layers as aforementioned.

3.4 Crystallization model

The predicted temperature distribution was forwarded to a non-isothermal crystallization model. The crystallization model was not fully coupled to the KOT model, e.g., to take into account latent heat release, as this would overcomplicate our selected approach. In this work, the model developed by Nakamura et al. [50] was employed, as it allows a relatively simple description of the evolution of the crystallinity under non-isothermal conditions. The relative degree of crystallinity (DoC) ξ was calculated based on the Avrami analytical theory [50, 51]:

$$ \xi(t)=\frac{\chi_{v}(t)}{\chi_{v\infty}}=1-exp(-\phi_{0}(t)) $$

(4)

where χ_v was the crystallized volume at time t and $\chi _{v\infty }$ was the crystallized volume in equilibrium conditions which was defined as the maximum value of crystallinity. Here, ϕ₀(t) was the expected relative crystallized volume if no impingement occurs for 3D spherulitic growth [52] and defined as:

$$ \phi_{0}(t)= \left( -{{\int}_{0}^{t}} \kappa(T)dt \right)^{n} $$

(5)

where κ was the temperature-dependent crystallization rate constant and the Avrami constant, n, was a measure for the nucleation and growth mechanism, e.g., n = 3 for spherulitic growth and heterogeneous nucleation. By substituting Eq. 5 into Eq. 4, the differential form of the Nakamura model can be achieved, which is convenient for computational implementation:

$$ \frac{d\xi(t)}{dt} = n\kappa(T)(1-\xi) (-log(1-\xi) )^{(n-1)/n} $$

(6)

Rate constant κ is conveniently related to the isothermal crystallization half time t_1/2, at which ξ(t_1/2) = 0.5, according to:

$$ \kappa(T)= (ln2)^{1/n} \frac{1}{t_{1/2}(T)} $$

(7)

The crystallization rate can be expressed in terms of the crystallization half-time using the classical Hoffman–Lauritzen theory. For PA12, isothermal crystallization experiments were used to express the t_1/2 of the pure polymer [53, 54].

$$ \frac{1}{t_{1/2}} = K_{0} \times exp \left( \!-\frac{U}{R(T-T_{\infty})} \right) \times exp \left( \!-\frac{K_{G}(T+T_{m})}{2T^{2} (T_{m}-T)} \right) $$

(8)

where U was the activation energy for crystallization, R was the universal gas constant, T_g was the glass transition temperature, and T_m was the equilibrium melting temperature while $T_{\infty }$ was the so-called Vogel temperature. The experimentally fitted parameters, i.e., K_G and K₀, were the growth rate constant and nucleation rate constant, respectively. All the required values were taken from [53] as U = 6270 J mol^− 1, R = 8.314 J mol^− 1K^− 1, $T_{\infty }=T_{g}-30K$, T_g = 60 ∘C, T_m = 190 ∘C, K_G = 109,258 K², and $K_{0}={8639}\textit {s}^{-1}$. The data in the literature concerning neat PA12 of type PA 2200 indicated an Avrami exponent was taken approximately as 2.82 [53, 54] suggesting a mixture of 2D and 3D crystal growth. Note that Eq. 6 was used between T_g and T_m to describe the non-isothermal crystallization growth. In this work, the influence of the fiber content in the prepreg tape on the crystallization behavior of PA12 is not taken into account. The model parameters were verified by comparing the modeled and the experimentally obtained peak crystallization temperature from DSC. Good agreement was obtained since a thermal profile with a constant cooling rate of 20 ∘C/min yielded a computed peak crystallization temperature of 151 ∘C while experimentally a value of 148 ∘C was shown.

During the LATW process, the temperature reaches well above melting temperature quite frequently. Thus, it is needed to describe the crystallization kinetics during the melting phase as studied in [33, 55, 56]. To simplify the melting kinetics, it was assumed that when the temperature was higher than T_m, the DoC was set to 1%, i.e., almost all the crystals were melted instantaneously. Although this was an extreme assumption, i.e., polymers typically show a melting trajectory with a peak temperature T_m, the basic trends could be predicted as illustrated in [33].

4 Results and discussions

4.1 KOT model output

The normalized absorbed heat flux by the substrate and tape surface along the winding direction is plotted in Fig. 8. The normalization was done based on the power intensity of the laser source which was 0.91 W mm^− 2. It is seen that the lengths of the heated regions were 35 mm and 70 mm for the substrate and tape, respectively. The substrate, tape, and roller received approximately 46.6%, 31.1%, and 13.6% of the total incident energy, respectively. The laser orientation was more perpendicular to the substrate surface than the tape; therefore, a higher heat flux was predicted for the substrate according to Fresnel’s law [44]. The magnitude of the heat flux considerably reduced near the nip point region for the tape due to the shadowing effect as well as the rapid reduction in the incident angle of the direct hit. The shadow region which is not irradiated by the laser may be present prior to the nip point depending on the local geometry as well as the position of the laser source [20, 48, 57].

Fig. 8

The substrate and tape averaged heat flux across the width as a function of distance to the nip point in the heating region. After 70 mm, the tape heat flux dropped to 0

The predicted temperature distribution in the thickness and width directions for the liner and the substrate is plotted in Fig. 9 during winding of rows 1 to 3 for layer 2 at the nip point, i.e., when the tape was deposited on the substrate. The substrate reached the maximum temperature as the substrate surface was fully irradiated by the laser source. The thermal contact resistance effect at the liner/layer 1 interface was visible from the large temperature gradient. The effect of adjacent heating is seen at the already deposited tape edges by the high temperature values. At the indicated left (point P2) and right zones (point P18), the substrate temperature reached a higher temperature than at the central zones (point P10) due to the adjacent heating. Since the laser spot width, i.e., 28 mm, was larger than the tape width, i.e., 20 mm, the sides of adjacent rows were also heated for 4 mm, as clearly seen in Fig. 9b and c.

Fig. 9

Temperature distribution at the nip point during winding a row 1/layer 2, b row 2/layer 2, and c row 3/layer 2

By unfolding the cylindrical domain, the tape and substrate surface temperature distributions in the winding and width directions are depicted in Fig. 10. The surface temperature of row 2 during winding of rows 1 to 3 of layer 2 is presented by three contour plots. The heating region (t1 to t2), consolidation region (t2 to t3), and cooling region (t3 to t1) are annotated accordingly. The temperature non-uniformity in the width direction of the heating region was more pronounced up to 530 ∘C compared to the consolidating and cooling regions. During winding of row 1, only the left zone (point P2) was heated as shown in Fig. 10a (top). During winding of row 2, all the zones (points P2, P10, and P18) were heated at the same time. The temperatures of left (point P2) and right (point P18) zones were higher than the central zone (point P10) during winding of row 3 as shown in Fig. 10a (bottom). The tape temperature distribution in the width direction was found to be almost constant throughout the process as shown in Fig. 10b with a maximum temperature of 400 ∘C at the nip point.

Fig. 10

The row 2 surface temperature distribution during winding of rows 1 to 3 of layer 2 indicating the heating, consolidation, and cooling regions. b The incoming tape surface temperature during heating phase

4.2 Surface temperature

The surface temperature history measured by the thermal imaging camera was used to get an insight into the inline surface temperature during the process and also verify the predictions presented in Section 4.1. Once the winding process was started, the tape accelerated to the intended feed rate, i.e., run-in phase. After this transition period, the temperature distribution reached a steady-state phase since all the geometrical, optical, and thermal parameters were constant during winding of a specific layer. Therefore, the temperature history was averaged based on 3 winding experiments in the steady-state duration with the assigned standard deviation as shown in Fig. 11.

Fig. 11

Comparison of the thermal imaging camera measurements with the model predictions across the substrate width during winding layer 5

The measured temperature distributions across the substrate width are plotted for two locations prior to the nip point, i.e., 20 mm and 30 mm away from the nip point in Fig. 11. The corresponding predicted temperature distribution included the entirety of row 2 and 4 mm of row 1 and 3 to cover the laser width spot, i.e., around 28 mm which can be also seen in Fig. 4a with the annotated adjacent heating zones. The temperature non-uniformity was clearly observed with a higher temperature on the left zone of row 2 (25–29 mm) and a part of row 1 (21–25 mm). However, the central zone (29–41 mm) and right zone (41–45 mm) of row 2 and part of row 3 (45–49 mm) had almost the same temperature according to the model predictions. Relatively lower temperatures were measured at the sides of the laser spot, i.e., 21–22 mm and 48–49 mm in Fig. 11, which was considered mainly due to the top-hat laser power distribution used in the experiments as depicted in Fig. 4b. In general, the developed KOT process model captured the experimentally observed phenomena quite well. The centerline temperature at 20 mm prior to the nip point was found to be approximately 75 ∘C higher than the temperature at 30 mm prior to the nip point. The scatter in the predicted temperature distribution was due to the scatter in the heat flux distribution obtained from the optical model as seen in Fig. 8. The KOT model overpredicted the temperature at the left zone as compared with the measured surface temperature. This was due to the fact that a uniform power distribution was employed in the KOT model, whereas it was a sort of top-hat distribution for the laser source.

4.3 Interface temperature

In addition to the temperature non-uniformity on the substrate surface, the temperature distribution was also studied through the thickness to understand and explain the thermal history more elaborately. The temperature history of the computational nodes across the substrate width was a straightforward way to quantify the temperature non-uniformity as a function of time and eventually compare with the thermocouple measurements. During winding of layer 4, one temperature peak, i.e., single-peak behavior, was observed as shown in Fig. 12 by the thermocouples TC1–TC3. The TC1 was heated during winding of row 1 (0–2 s), while TC2 and TC3 were heated during winding of row 2 (2–4 s). Considering the width of row 2 in Fig. 9, the temperature histories were predicted based on the location of point P10 which represents the central zone. On the other hand, two temperature peaks, i.e., double-peak behavior, were observed in the temperature history of TC1–TC3 during winding of layer 5 as seen in Fig. 13. The TC1 was heated two times during winding of rows 2 and 3 (2–6 s), while TC2 and TC3 were heated during winding of rows 1 and 2 (0–4 s). The double-peak behavior was due to the shift of layer 5 with respect to layer 4 in the axial winding direction as explained in Section 2. The corresponding predictions for the left (point P2) and right (point P18) zones were compared with TC2/TC3 and TC1, respectively. The shaded area for the measured temperature by the thermocouples covered the standard deviation of the three trials in Figs. 12 and 13. It is seen that the thermoplastic liner acted as an insulator which resulted in a relatively slower cooling after the peak temperature for TC1 than TC2 and TC3. It is also seen that the experimentally observed trends for the single- and double-peak behaviors of the temperature evolution were captured quite well with the developed KOT model. The discrepancies between the measured and predicted temperature values might be due to the uncertainties in the thermocouple locations during the winding experiments, the simplification of the winding angle, and/or the model parameters which were taken from literature.

Fig. 12

Comparing the temperature history of the thermocouple measurements with the predictions for single-peak behavior of TC1 to 3 during winding of layer 5. The experimental shaded area includes the information of the standard deviation of three trials

Fig. 13

Comparing the temperature history of the thermocouple measurements with the predictions for double-peak behavior of TC1 to 3 during winding of layer 5. The experimental shaded area includes the information of the standard deviation of three trials

The predicted single- and double-peak behaviors for the temperature histories are summarized in Fig. 14 based on the maximum temperature distribution for row 2 during the winding of layer 4. Here, the maximum temperature was reported at the layer 1/layer 2 interface for each control volume node used in the KOT model. For the nodes on the left zone of row 2, i.e., 0 to 4 mm, two temperature peaks (approximately 150 ∘C and 210 ∘C) were predicted during winding of rows 1 and 2. The second temperature peak was higher by approximately 60 ∘C than the first temperature peak. In the central zone, i.e., 5 to 14 mm, the single temperature peak behavior was predicted with a peak temperature of approximately 165 ∘C during winding of row 2. Two temperature peaks were also the case for the right zone, i.e., 15 to 20 mm with a value of 165 ∘C for the first peak and 195 ∘C for the second peak. However, the second temperature peak of the right zone was found to be lower compared to the left zone because the left zone was heated at the layer 3/layer 4 interface while for the right zone this was at the layer 4/layer 5. Therefore, less heat was conducted to the layer 1/layer 2 interface at the right zone since it was more into the depth as illustrated at the top of Fig. 14. The peak temperatures at both the 4- and 16-mm locations were found to be lower than the average of the left and right zones, respectively. This was due to the heat conduction in the width direction toward the relatively colder central zone.

Fig. 14

Temperature peaks predicted across the width of row 2 at layer 1/layer 2 interface during winding of layer 4

In Fig. 15, the predicted temperature peaks for all the interfaces from liner/layer 1 to layer 4/layer 5 are plotted during winding of layer 5 from left to right. The temperature of single peaks dropped approximately from 420 ∘C at the layer 4 surface to 105 ∘C at the interface of liner/layer 1. On the left zone of all interfaces, the second peaks were always higher than the first peaks except for the corner node at 0 mm. This was also the case for the right zone except at the layer 4/layer 5 interface where the second peaks were lower than the first peaks. The second peaks in the right zone took place only after the deposition of the incoming tape. Since the calculated deposited tape temperature at the nip line of 400 ∘C was lower than the temperature of the heated substrate surface, i.e., 420 ∘C, the value of the second peaks dropped for the layer 4/layer 5 and layer 3/layer 4 interfaces at the right zone.

Fig. 15

Predicted temperature peaks across the width of row 2 at various interfaces during winding rows 1 to 3 of layer 5 in the left to right direction

4.4 Crystallinity evolution

An insight on the DoC development was gained by employing the predicted temperature history in the non-isothermal crystallinity model. The temperature histories and corresponding crystallinity evolution of points P2, P10, and P18 of row 2 at layer 1/layer 2 interfaces are shown in Fig. 16 during winding of layers 2–5. The PA12 polymer crystallizes between T_g and T_m with various growth rates [53, 58] which is shown as the shaded area in Fig. 16.

Fig. 16

Temperature history of computational nodes at the layer 1/layer 2 interface during winding of layers 2 to 5 for three zones of the row 2 with respect to the crystallization window shown as the shaded area. The PA12 is thermally stable below 350 ∘C [46]

The temperature of point P2 was found to be higher than T_m for two times while winding row 1 of layers 2 and 3. This was the same case also for points P10 and P18 during winding of row 2 (note the large overlap between both points); however, the point P2 was remelted for three more times during the second heating of layers 2 to 4. In addition, point P18 was heated above T_m also for three times during winding of row 3. Therefore, points P2 and P18 were remelted for 5 times in total and point P10 only for 2 times.

It is worth mentioning that the temperature can reach above the thermal degradation or stability temperature as depicted in Fig. 16 due to multiple heatings. The temperature of point P2 was found to be above the stability temperature for about 0.19 s and this was approximately 0.068 s for points P10 and P18.

A closer look at the crystallinity evolution is provided in Fig. 17 as an exemplary result for the interface between layers 1 and 2. Only the relevant temperatures above T_g are considered; therefore, the cumulative time above T_g for each point is shown. The plotted temperature range on the y-axis was limited to temperatures that displayed relatively high crystal growth rates [53]. The temperature of point P2 was above T_m during the second heating for all the layers for a certain time period. Hence, for point P2, it is assumed that the DoC reached the minimum value of 1% at the end of winding of each layer and the crystals started to grow again during cooling phase. Therefore, only the last cooling cycle of point P2 contributed to the final DoC, i.e., 51–60 s. For point P18, a slightly different history was recorded and the re-crystallization took place after winding of layer 4 and during layer 5. Although, the point P10 re-crystallized during three consecutive layers of 3 to 5, almost the same DoC was predicted as point P18. This was due to the slower cooling rate after the second peak for point P18 than point P10 within the crystallization window. The temperature of initial sharp cooling was way above T_m for point 18 and the subsequent moderate cooling fell in the crystallization window while for point P10 the sharp cooling after the nip point was within the crystallization window, resulting in slower growth of crystals which was captured by the implemented crystallization model.

Fig. 17

Temperature and crystallinity evolution history of points a P2, b P10, and c P18 at the interface of the layer 1/layer 2

The resulting crystallization distribution of row 2 is visualized in Fig. 18 at the end of each layer which gives a global understanding of how the crystals were developed as a function of winding layers. The DoC variations in the through-thickness direction with the highest DoC close to the liner were 14% (0.08 to 0.07) and 875% (0.78 to 0.08) at the end of winding layers 2 and 5, respectively. Thus, the DoC variation in the through the thickness direction was found to be considerably larger as the number of wound layers increased. The winding of the subsequent layers annealed the first layer which allowed the crystals to grow from DoC = 0.08 at the end of winding layer 2 up to DoC = 0.78 at the end of winding layer 5 at x = 15.5 mm. Besides, the liner was pure thermoplastic acting as a thermal barrier leading to lower cooling rate and therefore higher DoC.

Fig. 18

The cross-sectional distribution of the crystallinity degree of the row 2 after winding of layers 2–5

In the width direction, however, the maximum DoC variation for layers 1 and 5 was approximately 270% (0.78 to 0.21) and 167% (0.08 to 0.03) at the end of winding layer 5, respectively. The maximum DoCs were predicted at x = 4.5 mm and x = 15.5 mm across the substrate width. At the end of winding layer 5, the averaged DoC of the left and right zones were 0.12 and 0.14, respectively. For the central zone, the mean DoC was lower and equaled to 0.1 as shown in Fig. 18. This suggests that the double heating increased the relative DoC level in general.

The measured DoC for left, central, and right zones of the row 2 are depicted in Fig. 19. In order to compare the predicted DoC with the measured one, the average DoC of the calculation nodes within each zone as annotated in 18 was calculated. Reasonable agreement is seen regarding the trend of average crystallinity distribution through the investigated zones as the central zone had the least DoC = 0.53 and the right side had the highest DoC = 0.58 based on the performed DSC analysis. On the other hand, a discrepancy can be observed between the overall predicted and experimental values. As the input parameters for the used crystallization model were verified experimentally, we further investigated the influence of the programmed melting behavior. The measured DoC were in between two extreme cases, one where no melting took place and one case where melting of all crystals was set once the temperature reached above the melting temperature (current situation). The experimental values from DSC were closer to the case without any melting. It is likely that, during the LATW process, the amount of melting is very low due to the rapid heating rates and short durations above the melting temperature. Also, it is known that incomplete melting of crystals increases the rate of crystallization during subsequent cooling as the (partially molten) crystals act as nucleating agents, increasing the final crystallinity in a layer [59]. The consequence of incomplete melting on crystallization during cooling shows the importance of the melting behavior during LATW process, which needs to be considered for a more realistic crystallinity prediction.

Fig. 19

A comparison between measured and predicted average DoC for each investigated zone considering two extreme melting behaviors for the crystallinity model

5 Conclusion

The temperature and crystallization evolution during the LATW process with adjacent hoop pattern were investigated both experimentally and numerically for manufacturing of C/PA12 pipes. A numerical KOT model was developed considering the substrate mass growth both in thickness and in-plane directions. Besides, the anisotropic reflections of laser rays were modeled leading to an accurate prediction of absorbed heat flux on the substrate and tape surfaces. The crystallinity distribution was predicted by forwarding the KOT model to a non-isothermal crystallization model taking the melting kinetics into account. The temperate history was well captured during manufacturing of three small pipes by means of thermocouples in the through-thickness direction. The temperature distributions on the substrate surface were obtained by utilizing a thermal imaging camera. The KOT model was validated by comparing the temperature predictions with the experimentally measured temperature.

Multiple heating and cooling histories at the edges of the substrate were captured by the temperature measurements and predictions which resulted in significant temperature gradients for the substrate in the width direction. The edges of the substrate were heated two times which resulted in a temperature increase of approximately 50 ∘C at the edges as compared with the central region of the substrate. The non-uniform temperature distribution caused a non-uniform distribution of the degree of crystallinity across the width of substrate. It was found that the layers close to the liner had a higher degree of crystallinity up to 0.78 due to the annealing effect during winding of subsequent layers. The maximum crystallinity variations in the width and through-thickness directions were found to be of 270% and 875% at the end of winding of layer 5, respectively. A comparison between the measured and predicted degree of crystallinity across the width of the substrate was made with agreements in the trends. In this work, the rate of melting was overestimated. It is likely that limited melting occurred due to the high heating rates and short melting times throughout the process. It was shown that the melting behavior should be considered in more detail for a more realistic prediction. It was observed that complex temperature and crystallinity distributions were obtained even with constant process parameters during adjacent hoop winding of tapes. Therefore, the heat flux distribution on the substrate needs to be optimized by creating a near-uniform laser power distribution instead of top-hat distribution with the same laser spot width as the prepreg width to minimize the temperature and crystallinity gradients across the wound tape. The developed KOT model paves the road toward an accurate process design tool for reliable manufacturing of continuous thermoplastic pipes with high and uniform quality. The accuracy of the KOT model can be further improved by taking different winding angles into account causing a change to the illuminated substrate geometry, which is considered a future work.