Ensemble transfer learning for refining stability predictions in milling using experimental stability states

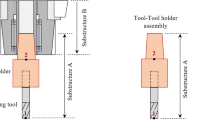
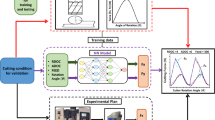
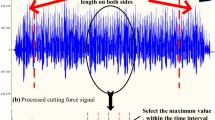
Abstract

A new approach for updating model-based stability chart predictions in milling based on experimental data is presented. The approach utilizes Deep Neural Networks (DNNs), which are pre-trained with simulated data that is generated by predicting machine dynamics through receptance coupling and evaluating stability through an analytical stability model. The weights in the DNN are fine-tuned by re-training the networks with a small experimental dataset containing only a few dozen samples. Target is to match network predictions with the experimentally observed stability states acquired under different cutting conditions. The presented approach avoids measurement or model-based estimation of cutting force coefficients as well as the measurement of tooltip dynamics or extensive model parameter identification, making it an attractive approach for industrial applications. In an experimental validation, where stability charts for various engagement conditions and different tool clamping lengths are predicted, a good match between predictions and experimental stability limits is achieved. It is shown that an ensemble learning method, where predictions of multiple networks are combined, can improve prediction accuracy. Furthermore, it is demonstrated that the new approach requires approximately five times fewer experimental samples than previously proposed model-free machine learning approaches to reach the same prediction accuracy on a test set.