Skip to main content

Advertisement

SpringerLink
Log in

A bi-objective model for a multi-echelon supply chain design considering efficiency and customer satisfaction: a case study in plastic parts industry

  • ORIGINAL ARTICLE
  • Published:
The International Journal of Advanced Manufacturing Technology Aims and scope Submit manuscript

Abstract

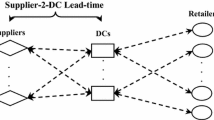
One of the fundamental challenges of today’s manufacturing systems is the contradiction between cost efficiency and customer satisfaction. Finding a good balance between good customer satisfaction and supply chain efficiency is a critical problem in the supply chain management. To achieve this goal, a bi-objective mathematical model is suggested in this paper to maximize the efficiency of network and also customer satisfaction. This multi-period and multi-product supply chain network design model consists of suppliers, factories, distribution centers (DCs), and customers. The proposed bi-objective mixed-integer non-linear programming (MINLP) model is a member of the NP-hard class of optimization problems. Hence, two well-known multi-objective metaheuristic algorithms namely, Non-dominated Sorting Genetic Algorithm II (NSGA-II) and Non-dominated Ranked Genetic Algorithm (NRGA) are employed to solve the proposed model. The author uses Taguchi method for tuning the parameters of algorithms in order to achieve better performances. Moreover, a case study in the plastic industry is performed to collect data from the north region of Iran. Some well-known multi-objective metrics such as analysis of variance (ANOVA) is used to measure the performance of the proposed framework. Finally, results demonstrate the efficiency of the proposed framework.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Pham T, Yenradee P (2017) Optimal supply chain network design with process network and BOM under uncertainties: a case study in toothbrush industry. Comput Ind Eng 108:177–191

    Article  Google Scholar 

  2. Cheraghalipour A, Paydar MM, Hajiaghaei-keshteli M (2017) An integrated approach for collection center selection in reverse logistics. Int J Eng Trans A Basics 30(7):1005–1016

    Google Scholar 

  3. Sarrafha K, Rahmati SHA, Niaki STA, Zaretalab A (2015) A bi-objective integrated procurement, production, and distribution problem of a multi-echelon supply chain network design: a new tuned MOEA. Comput Oper Res 54:35–51

    Article  MathSciNet  MATH  Google Scholar 

  4. Randall TR, Morgan RM, Morton AR (2003) Efficient versus responsive supply chain choice: an empirical examination of influential factors. J Prod Innov Manag 20(6):430–443

    Article  Google Scholar 

  5. Altiparmak F, Gen M, Lin L, Paksoy T (2006) A genetic algorithm approach for multi-objective optimization of supply chain networks. Comput Ind Eng 51(1):196–215

    Article  Google Scholar 

  6. Xu J, Liu Q, Wang R (2008) A class of multi-objective supply chain networks optimal model under random fuzzy environment and its application to the industry of Chinese liquor. Inf Sci 178(8):2022–2043

    Article  MATH  Google Scholar 

  7. Azaron A, Brown KN, Tarim SA, Modarres M (2008) A multi-objective stochastic programming approach for supply chain design considering risk. Int J Prod Econ 116(1):129–138

    Article  Google Scholar 

  8. Wang F, Lai X, Shi N (2011) A multi-objective optimization for green supply chain network design. Decis Support Syst 51(2):262–269

    Article  Google Scholar 

  9. Almaktoom AT, Krishnan KK, Wang P, Alsobhi S (2014) Assurance of system service level robustness in complex supply chain networks. Int J Adv Manuf Technol 74(1–4):445–460

    Article  Google Scholar 

  10. Almaktoom AT, Krishnan KK, Wang P, Alsobhi S (2016) Cost efficient robust global supply chain system design under uncertainty. Int J Adv Manuf Technol 85(1–4):853–868

    Article  Google Scholar 

  11. Farahani RZ, Rezapour S, Drezner T, Fallah S (2014) Competitive supply chain network design: an overview of classifications, models, solution techniques and applications. Omega 45:92–118

    Article  Google Scholar 

  12. Eskandarpour M, Dejax P, Miemczyk J, Péton O (2015) Sustainable supply chain network design: an optimization-oriented review. Omega 54:11–32

    Article  Google Scholar 

  13. Ghaderi H, Pishvaee MS, Moini A (2016) Biomass supply chain network design: an optimization-oriented review and analysis. Ind Crop Prod 94:972–1000

    Article  Google Scholar 

  14. Ghomi-Avili M, Jalali Naini SG, Tavakkoli-Moghaddam R, Jabbarzadeh A (2017) A network design model for a resilient closed-loop supply chain with lateral transshipment. Int J Eng 30(3):374–383

    Google Scholar 

  15. Karabakal N, Günal A, Ritchie W (2000) Supply-chain analysis at Volkswagen of America. Interfaces (Providence) 30(4):46–55

    Article  Google Scholar 

  16. Verter V, Dasci A (2002) The plant location and flexible technology acquisition problem. Eur J Oper Res 136(2):366–382

    Article  MATH  Google Scholar 

  17. Yeh W-C (2005) A hybrid heuristic algorithm for the multistage supply chain network problem. Int J Adv Manuf Technol 26(5–6):675–685

    Article  Google Scholar 

  18. Choi J, Lee H, Heo S, Lee J (2006) A mathematical programming for supply chain network design, in 2006 SICE-ICASE International Joint Conference, pp 170–174

  19. Lee J-H, Moon I-K, Park J-H (2010) Multi-level supply chain network design with routing. Int J Prod Res 48(13):3957–3976

    Article  MATH  Google Scholar 

  20. Jabbarzadeh A, Fahimnia B, Seuring S (2014) Dynamic supply chain network design for the supply of blood in disasters: a robust model with real world application. Transport Res E Log Transport Rev 70:225–244

    Article  Google Scholar 

  21. Anne KR, Chedjou JC, Kyamakya K (2009) Bifurcation analysis and synchronisation issues in a three-echelon supply chain. Int J Log Res Appl 12(5):347–362

    Article  Google Scholar 

  22. Ramezani M, Bashiri M, Tavakkoli-Moghaddam R (2013) A robust design for a closed-loop supply chain network under an uncertain environment. Int J Adv Manuf Technol 66(5–8):825–843

    Article  MATH  Google Scholar 

  23. Khalili-Damghani K, Tavana M, Amirkhan M (2014) A fuzzy bi-objective mixed-integer programming method for solving supply chain network design problems under ambiguous and vague conditions. Int J Adv Manuf Technol 73(9–12):1567–1595

    Article  Google Scholar 

  24. Dubey R, Gunasekaran A, Childe SJ (2015) The design of a responsive sustainable supply chain network under uncertainty. Int J Adv Manuf Technol 80(1–4):427–445

    Article  Google Scholar 

  25. Varsei M, Polyakovskiy S (2017) Sustainable supply chain network design: a case of the wine industry in Australia. Omega 66:236–247

    Article  Google Scholar 

  26. Özceylan E, Demirel N, Çetinkaya C, Demirel E (2016) A closed-loop supply chain network design for automotive industry in Turkey. Comput Ind Eng 113:727–745 https://doi.org/10.1016/j.cie.2016.12.022

  27. de Keizer M, Groot JJ, Bloemhof J, van der Vorst JGAJ (2014) Logistics orchestration scenarios in a potted plant supply chain network. Int J Log Res Appl 17(2):156–177

    Article  Google Scholar 

  28. Benyoucef L, Xie X, Tanonkou GA (2013) Supply chain network design with unreliable suppliers: a Lagrangian relaxation-based approach. Int J Prod Res 51(21):6435–6454

    Article  Google Scholar 

  29. Yi P, Huang M, Guo L, Shi T (2016) A retailer oriented closed-loop supply chain network design for end of life construction machinery remanufacturing. J Clean Prod 124:191–203

    Article  Google Scholar 

  30. Dubey R, Gunasekaran A (2015) Retracted article: Sustainable supply chain network design: a case of Indian company. Int J Log Res Appl 18(5):1–23

    Google Scholar 

  31. Zhang L, Zhou Y (2012) A new approach to supply chain network equilibrium models. Comput Ind Eng 63(1):82–88

    Article  Google Scholar 

  32. Taxakis K, Papadopoulos C (2016) A design model and a production–distribution and inventory planning model in multi-product supply chain networks. Int J Prod Res 54(21):6436–6457

    Article  Google Scholar 

  33. Farrokh M, Azar A, Jandaghi G, Ahmadi E (2017) A novel robust fuzzy stochastic programming for closed loop supply chain network design under hybrid uncertainty. Fuzzy Sets Syst (in press https://doi.org/10.1016/j.fss.2017.03.019)

  34. Deb K, Pratap A, Agarwal S, Meyarivan T (2002) A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans Evol Comput 6(2):182–197

    Article  Google Scholar 

  35. Al Jadaan O, Rao CR, Rajamani L (2008) Non-dominated ranked genetic algorithm for solving multi-objective optimization problems: NRGA. J Theor Appl Inf Technol 4(1):60–67

    Google Scholar 

  36. Rahmati SHA, Hajipour V, Niaki STA (2013) A soft-computing Pareto-based meta-heuristic algorithm for a multi-objective multi-server facility location problem. Appl Soft Comput J 13(4):1728–1740

    Article  Google Scholar 

  37. Karimi N, Zandieh M, Karamooz HR (2010) Bi-objective group scheduling in hybrid flexible flowshop: a multi-phase approach. Expert Syst Appl 37(6):4024–4032

    Article  Google Scholar 

  38. Taguchi G (1986) Introduction to quality engineering: designing quality into products and processes, Illustrate. The Organization, White Plains

    Google Scholar 

  39. Maghsoudlou H, Kahag MR, Niaki STA, Pourvaziri H (2016) Bi-objective optimization of a three-echelon multi-server supply-chain problem in congested systems: modeling and solution. Comput Ind Eng 99:41–62

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Industrial Engineering, K. N. Toosi University of Technology, Pardis St. Molasadra Ave., Vanak Sq, Tehran, 19395-1999, Iran

    Seyed Babak Ebrahimi

Authors
  1. Seyed Babak Ebrahimi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Seyed Babak Ebrahimi.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ebrahimi, S.B. A bi-objective model for a multi-echelon supply chain design considering efficiency and customer satisfaction: a case study in plastic parts industry. Int J Adv Manuf Technol 95, 3631–3649 (2018). https://doi.org/10.1007/s00170-017-1437-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00170-017-1437-0

Keywords

Search

Navigation