Abstract
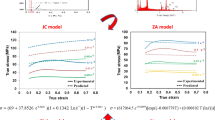
This work presents description and comparison of internal and state variable models of flow stress in varying processing conditions. Three models were analyzed. The first one is based on dislocation theory and describing the mechanical behavior of f.c.c. polycrystalline structures. The second and third models are standard and modified Sellars’ flow stress models. Models were adapted for two commercial codes based on finite element method: QForm7 and Forge 2005. The compression test of 45 grade steel with instant changes of strain rate was simulated. Calculated compression force and flow stress were compared with the experimental data from plastometric tests. The forging process was simulated by QForm7. Results obtained by both internal and modified Sellars’ models confirm their high accuracy for analysis and prediction of the flow stress under the varying deformation conditions.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
References
Kocks UF (1976) Laws for work-hardening and low-temperature creep. J Eng Mater Technol 98:76–85. doi:10.1115/1.3443340
Roberts W (1984) Dynamic changes that occur during hot working and their significance regarding microstructural development and hot workability. In: Krauss G (ed) Deformation, processing and structure, ASM, Metals Park OH, pp 109–184
Yoshie A, Morikawa H, Onoe Y (1987) Formulation of static recrystallization of austenite in hot rolling process of steel plate. Trans ISIJ 27:425–431
Bergström Y (1969/70) Dislocation model for the stress-strain behaviour of polycrystalline α-Fe with special emphasis on the variation of the densities of mobile and immobile dislocations. Mater Sci Eng 5:193–200
Estrin Y, Mecking H (1984) A unified phenomenogical description of work hardening and creep based on one parameter models. Acta Metall 29:57–70. doi:10.1016/0001-6160(84)90202-5
Kocks UF, Mecking H (2003) Physics and phenomenology of strain hardening: the FCC case. Prog Mater Sci 48:171–273. doi:10.1016/S0079-6425(02)00003-8
Estrin Y, Tóth LS, Molinari A, Bréchet Y (1998) A dislocation-based model for all hardening stages in large strain deformation. Acta Mater 46:5509–5522. doi:10.1016/S1359-6454(98)00196-7
Roters F, Raabe D, Gottstein G (2000) Work hardening in heterogeneous alloys—a microstructural approach based on three internal state variables. Acta Mater 48:4181–4189. doi:10.1016/S1359-6454(00)00289-5
Van Houtte P, Van Bael A, Seefeldt M (2007) The application of multiscale modelling for the prediction of plastic anisotropy and deformation textures. Mater Sci Forum 550:13–22. doi:10.4028/www.scientific.net/MSF.550.13
Sandström R, Lagneborg R (1975) A model for hot working occurring by recrystallization. Acta Metall 23:387–398. doi:10.1016/0001-6160(75)90132-7
Roucoules C, Pietrzyk M, Hodgson PD (2003) Analysis of work hardening and recrystallization during the hot working of steel using a statistically based internal variable model. Mater Sci Eng A 339:1–9. doi:10.1016/S0921-5093(02)00120-X
Ordon J, Kuziak R, Pietrzyk M (2000) History dependent constitutive law for austenitic stainless steels. In: Pietrzyk M, Kusiak J, Majta J, Hartley P, Pillinger I (eds.) Proceedings of metal forming 2000, Krakow, pp 747–753
Estrin Y (1996) Dislocation density-related constitutive modeling. In: Krausz AS, Krausz K (eds) Unified constitutive law of plastic deformation. Academic, San Diego, pp 69–106
Svyetlichnyy DS (2005) The coupled model of a microstructure evolution and a flow stress based on the dislocation theory. ISIJ Int 45:1187–1193. doi:10.2355/isijinternational.45.1187
Svyetlichnyy DS (2009) Modification of coupled model of microstructure evolution and flow stress: experimental validation. Mater Sci Technol 25:981–988. doi:10.1179/174328408X317084
Svyetlichnyy DS, Majta J, Nowak J (2013) A flow stress for the deformation under varying condition—internal and state variable models. Mater Sci Eng A 576:140–148. doi:10.1016/j.msea.2013.04.007
Taylor GI (1934) The mechanism of plastic deformation of crystals. Part I. Theoretical. Proc Roy Soc A 145:362–387. doi:10.1098/rspa.1934.0106
Sellars CM (1990) Modelling microstructural development during hot rolling. J Mater Sci Technol 6:1072–1081. doi:10.1179/mst.1990.6.11.1072
Qian M, Guo ZX (2004) Cellular automata simulation of microstructural evolution during dynamic recrystallization of an HY-100 steel. Mater Sci Eng A 365:180–185. doi:10.1016/j.msea.2003.09.025
Svyetlichnyy DS (2010) Modelling of the microstructure: from classical cellular automata approach to the frontal one. Comput Mater Sci 50:92–97. doi:10.1016/j.commatsci.2010.07.011
Svyetlichnyy DS (2012) Simulation of microstructure evolution during shape rolling with the use of frontal cellular automata. ISIJ Int 52:559–568. doi:10.2355/isijinternational.52.559
Svyetlichnyy DS (2012) Reorganization of cellular space during the modeling of the microstructure evolution by frontal cellular automata. Comput Mater Sci 60:153–162. doi:10.1016/j.commatsci.2012.03.029
Davenport SB, Silk NJ, Sparks CN, Sellars CM (2000) Development of constitutive equations for modelling of hot rolling. Mater Sci Technol 16:539–546. doi:10.1179/026708300101508045
Sellars CM, Tegart WJ, Mc G (1966) La relation entre la resistance et la structure dans la deformation a chaud. Mem Sci Rev Metall 63:731–746
Malinowski Z (2001) Analysis of temperature fields in the tools during forging of axially symmetrical parts. Arch Metall 46:93–118
Malinowski Z, Rywotycki M (2009) Modeling of the strand and mold temperature in the continuous steel caster. Arch Civ Mech Eng 9:59–73. doi:10.1016/S1644-9665(12)60060-0
Bíró T, Csizmadia J (2012) Recent technique for thermal-fatigue simulation of heat-resistant steels. Mech Eng 56:105–110. doi:10.3311/pp.me.2012-2.05
Shida S (1968) Effect of carbon content, temperature and strain rate on compressive flow-stress of carbon steel (Resistance to deformation of carbon steels at elevated temperature, 1st report). J JSTP 9:127–132
Perig AV, Golodenko NN (2014) CFD 2D simulation of viscous flow during ECAE through a rectangular die with parallel slants. Int J Adv Manuf Technol 74:943–962. doi:10.1007/s00170-014-5827-2
Stebunov S, Biba N, Ovchinnikov A, Smelev V (2007) Application of QForm forging simulation system for prediction of microstructure of aluminium forged parts. Comp Meth Mater Sci 7:1–5
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Svyetlichnyy, D., Nowak, J., Biba, N. et al. Flow stress models for deformation under varying condition—finite element method simulation. Int J Adv Manuf Technol 87, 543–552 (2016). https://doi.org/10.1007/s00170-016-8506-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00170-016-8506-7