Skip to main content
SpringerLink
Log in

Makespan minimization in a job shop with a BPM using simulated annealing

  • ORIGINAL ARTICLE
  • Published:
The International Journal of Advanced Manufacturing Technology Aims and scope Submit manuscript

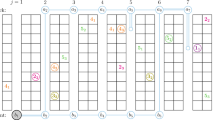
Abstract

A scheduling problem commonly observed in the metal working industry has been studied in this research effort. A job shop equipped with one batch processing machine (BPM) and several unit-capacity machines has been considered. Given a set of jobs, their process routes, processing requirements, and size, the objective is to schedule the jobs such that the makespan is minimized. The BPM can process a batch of jobs as long as its capacity is not exceeded. The batch processing time is equal to the longest processing job in the batch. If no batches were to be formed, the scheduling problem under study reduces to the classical job shop problem with makespan objective, which is known to be nondeterministic polynomial time-hard. A network representation of the problem using disjunctive and conjunctive arcs, and a simulated annealing (SA) algorithm are proposed to solve the problem. The solution quality and run time of SA are compared with CPLEX, a commercial solver used to solve the mathematical formulation and with four dispatching rules. Experimental study clearly highlights the advantages, in terms of solution quality and run time, of using SA to solve large-scale problems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Pinedo M (2002) Scheduling theory, algorithms, and systems, Secondth edn. Prentice-Hall, Upper Saddle River

    MATH  Google Scholar 

  2. Mason SJ, Fowler JW (2000) Maximizing delivery performance in semiconductor wafer fabrication facilities. Simul Conf Proc 2:1458–1463, o.2

    Google Scholar 

  3. Mason SJ, Fowler JW, Carlyle WM, Montgomery DC (2005) Heuristics for minimizing total weighted tardiness in complex job shops. Int J Prod Res 43(10):1943–1963

    Article  MATH  Google Scholar 

  4. Gupta AK, Sivakumar AI (2006) Job shop scheduling techniques in semiconductor manufacturing. Int J Adv Manuf Technol 27(11–12):1163–1169

    Article  Google Scholar 

  5. Ovacik IM, Uzsoy R (1997) Decomposition methods for complex factory scheduling problems. Kluwer, Boston

    Book  Google Scholar 

  6. Fang L, Luh PB, Chen H (2000) Improving the Lagrangian relaxation approach for large job-shop scheduling. 39th IEEE Conference on Decision and Control; Dec 12–15 2000; Sydney, NSW: Institute of Electrical and Electronics Engineers Inc.

  7. Mason SJ, Fowler JW, Carlyle WM (2002) A modified shifting bottleneck heuristic for minimizing total weighted tardiness in complex job shops. J Sched 5(3):247–262

    Article  MathSciNet  MATH  Google Scholar 

  8. Mönch L, Driessel R (2005) A distributed shifting bottleneck heuristic for complex job shops. Comput Ind Eng 49(3):363–380

    Article  Google Scholar 

  9. Uzsoy R, Wang CS (1997) Decomposition procedures for global scheduling of complex job shops. Proceedings of the 1997 21st IEEE/CPMT International Electronics Manufacturing Technology (IEMT) Symposium; Oct 13–15 1997; Austin, TX, USA: IEEE, Piscataway, NJ, USA

  10. Demirkol E, Mehta S, Uzsoy R (1997) A computational study of shifting bottleneck procedures for shop scheduling problems. J Heuristics 3(2):111–137

    Article  MATH  Google Scholar 

  11. Uzsoy R, Wang CS (2000) Performance of decomposition procedures for job shop scheduling problems with bottleneck machines. Int J Prod Res 38(6):1271–1286

    Article  MATH  Google Scholar 

  12. Sun T, Luh PB, Liu M (2006) Lagrangian relaxation for complex job shop scheduling. Proceedings of the 2006 IEEE International Conference on Robotics and Automation, ICRA 2006; May 15–19 2006; Orlando, FL, USA: Institute of Electrical and Electronics Engineers Inc., Piscataway, NJ 08855–1331, USA

  13. Kaskavelis CA, Caramanis MC (1998) Efficient Lagrangian relaxation algorithms for industry size job-shop scheduling problems. IIE Trans (Inst Ind Eng) 30(11):1085–1097

    Google Scholar 

  14. Pfund ME, Balasubramanian H, Fowler JW, Mason SJ, Rose O (2008) A multi-criteria approach for scheduling semiconductor wafer fabrication facilities. J SCHED 11(1):29–47

    Article  MATH  Google Scholar 

  15. Damodaran P and Rojas M (2011). Mathematical formulation to minimize makespan in a job shop with a batch processing machine. Ninth LACCEI Latin American and Caribbean Conference (LACCEI'2011), Engineering for a Smart Planet. http://www.laccei.org/LACCEI2011-Medellin/…/PE166_Rojas.pdf. Accessed 25 Jan 2012

  16. Kirkpatrick S, Gelatt CD, Vecchi MP (1983) Optimization by simulated annealing. Science 220:671–680

    Article  MathSciNet  MATH  Google Scholar 

  17. Cerny V (1985) A thermodynamical approach to the traveling salesman problem: an efficient simulation algorithm. J Optim Theory Appl 45:41–51

    Article  MathSciNet  MATH  Google Scholar 

  18. Yamada T, Nakano R (1996) Job shop scheduling by simulated annealing combined with deterministic local search, meta-heuristics: theory and applications. Kluwer, MA, pp 237–248

    Google Scholar 

  19. Fattahi P, Mehrabad MS, Jolai F (2007) Mathematical modeling and heuristic approaches to flexible job shop scheduling problems. J Intell Manuf 18(3):331–342

    Article  Google Scholar 

  20. Chung SH, Tai YT, Pearn WL (2008) Minimising makespan on parallel batch processing machines with non-identical ready time and arbitrary job sizes. Int J Prod Res. doi:10.1080/00207540802010807

  21. Yao AC (1980) New algorithms for bin packing. J ACM 27(2):207–227

    Article  MATH  Google Scholar 

  22. Askin R, Standridge C (1993) Modeling and analysis of manufacturing systems. Wiley, New York, 451 p

    MATH  Google Scholar 

  23. Beasley JE (1990). Set of 82 JSP test instances. OR-library: http://people.brunel.ac.uk/~mastjjb/jeb/orlib/files/jobshop1.txt. Accessed 30 June 2009

  24. Panwalkar SS, Iskander W (1977) A survey of scheduling rules. Oper Res 25:45–61

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Departamento de Ingeniería Industrial, Universidad del Norte, Km. 5 Vía Puerto Colombia, Barranquilla, Colombia

    Miguel Rojas-Santiago

  2. Industrial and Systems Engineering, Northern Illinois University, Dekalb, IL, 60115, USA

    Purushothaman Damodaran

  3. Department of Technology, Northern Illinois University, Dekalb, IL, 60115, USA

    Shanthi Muthuswamy

  4. Departamento de Ingeniería de Producción, Universidad EAFIT, Carrera 49 #7 sur 50, Medellín, Colombia

    Mario C. Vélez-Gallego

Authors
  1. Miguel Rojas-Santiago
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Purushothaman Damodaran
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Shanthi Muthuswamy
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Mario C. Vélez-Gallego
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Miguel Rojas-Santiago.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Rojas-Santiago, M., Damodaran, P., Muthuswamy, S. et al. Makespan minimization in a job shop with a BPM using simulated annealing. Int J Adv Manuf Technol 68, 2383–2391 (2013). https://doi.org/10.1007/s00170-013-4858-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00170-013-4858-4

Keywords

Search

Navigation