Abstract
With Bertrand-Nash mill-price competition, travel costs proportional to distance squared, and three firms on an interval, the equilibrium locations of the peripheral firms are further from the center than is socially optimal. If there is a central intersection, with four (or more) finite roadway segments radiating outward from the center (a small city spread along two intersecting roadways), and with one firm at the center and one on each radial segment, then the equilibrium locations of the peripheral firms are closer to the center than is socially optimal. Extensions include competition with spatial price discrimination, a more complicated system of intersecting roadways, and more than one firm on each roadway segment.
Similar content being viewed by others
Notes
For Bertrand-Nash mill-pricing models with linear transportation costs, see also the duopoly-line-segment models in part of d’Aspremont et al. (1979) and (Anderson et al. (1992), pp. 293–297), and the multi-firm and many-firm models (using circles, line segments, and infinite lines) of (Vickrey (1964), pp. 334–336, 1999, pp. 960–962), Salop (1979), Mulligan (1996), and Capozza and Van Order (1980). In Hotelling (1929), each firm moves toward the center if firms are not closer than (0.25, 0.75). However, d’Aspremont et al. (1979) show that a Bertrand-Nash equilibrium in mill prices does not exist once firms are closer than this (see also Vickrey 1964, p. 327), unless both firms are at the center and charge zero prices. Thus, no subgame-perfect Nash equilibrium in locations exists either.
Many authors have Bertrand-Nash mill pricing and transportation costs proportional to distance squared, including the duopoly-line-segment models in (d’Aspremont et al. (1979), pp. 1148–1149), (Anderson et al. (1992), pp. 298–299); Lambertini (1994); Lambertini (1997), Tabuchi and Thisse (1995), Meza and Tombak (2009), Matsumura and Matsushima (2009), Egger and Egger (2010) and Braid (2011), and the multi-firm and many-firm models in Neven (1987), (Anderson et al. (1992), pp. 299–301), Brenner (2005), Eaton and Wooders (1985), and Economides (1989).
With linear transportation costs, nonexistence presumably also applies if firms are on intersecting finite line segments. Bertrand-Nash mill-pricing models with linear transportation costs and networks of intersecting roadways include Fik (1991), Fik and Mulligan (1991), and Braid (1993), which assume exogenous firm locations, and Sect. 6 of Mulligan (1996), which presents an analysis with endogenous locations.
This is in fact similar to an exercise performed in Fik (1991). There is a complicated network of roadways, and the total length of all roadway segments (not the length of each segment) is held constant as the number of segments becomes large.
For example, with five firms, the socially optimal locations on a unit interval are (0.1, 0.3, 0.5, 0.7, 0.9), but the equilibrium locations are (0.104, 0.329, 0.500, 0.671, 0.896).
DeGraba (1987) also considers a national firm that charges different prices in different cities. This pricing assumption is not very relevant to my paper, since it would require that the central store can charge different mill prices to consumers living on different roadway segments.
My Sects. 3–4 can be used to extend DeGraba (1987) in a way not considered at all in his paper. My Proposition 2 (which has \(n = 2\)) can be interpreted as a national firm at location 0 in the middle of a line-segment product space of length 2, competing with one firm on each side in a single city. Suppose there are \(m = n/2\) cities (for any even \(n\)). My Proposition 3 can be interpreted as a national firm at location 0 competing with local firms on each side in \(m = 2\) cities (a total of four local firms), if the national firm is constrained to set a single mill price for both cities. Proposition 4 can be interpreted in an analogous way. Propositions 1 and 5, which present the socially optimal locations and compare them to the equilibrium locations, are applicable here.
See also Hurter and Lederer (1985), Lederer and Hurter (1986), MacLeod et al. (1988), Sect. 4 of Hamilton et al. (1989), (Anderson et al. (1992), pp. 325–330), Gupta (1992), Sect. 3 of Yu (2007), Braid (2008), and Heywood and Ye (2009). I use “firm” instead of “store,” since spatial price discrimination is more likely to be used by a firm that pours concrete or delivers a bulky item than a restaurant or a store where a consumer eats a meal or carries the goods home.
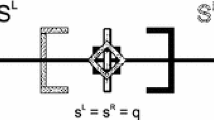
It is useful to recall from Sect. 4 that with three roadway segments and a single intersection, and with a single store at the center, the equilibrium has \(a = b = 8/13 = 0.6154\).
If \(R = 1\), then \(a = b = 0.6207\), so an increase in \(R\) does not always decrease the equilibrium value of a, something that is also shown in the second model below.
Models of spatial competition with mill pricing usually assume that \(\alpha = 1\) or \(\alpha = 2\) because these are the most convenient to work with. I am not aware of empirical evidence, but for shopping trips, a value of \(\alpha \) significantly greater than 1 is likely to be most realistic when consumers must walk (particularly if they have to carry something home).
For example, see Hsu (1983), who considers spatial monopoly with a general population density function that might be negative exponential.
See also (Fujita and Thisse (2002), Chapter 7).
References
Anderson SP (1988) Equilibrium existence in the linear model of spatial competition. Economica 55:479–491
Anderson SP, de Palma A, Thisse J-F (1992) Discrete choice theory of product differentiation. M.I.T Press, Cambridge
Ben-Akiva M, de Palma A, Thisse J-F (1989) Spatial competition with differentiated products. Reg Sci Urban Econ 19:5–19
Braid RM (1989) Retail competition along intersecting roadways. Reg Sci Urban Econ 19:107–112
Braid RM (1993) Spatial price competition with consumers on a plane, at intersections, and along main roadways. J Reg Sci 33:187–205
Braid RM (2008) Spatial price discrimination and the locations of firms with different product selections or product varieties. Econ Lett 98:342–347
Braid RM (2011) Bertrand-Nash mill pricing and the locations of two firms with partially overlapping product selections. Pap Reg Sci 90:197–211
Brenner S (2005) Hotelling games with three, four, and more players. J Reg Sci 45:851–864
Caplin AS, Nalebuff BJ (1991) Aggregation and imperfect competition: on the existence of equilibrium. Econometrica 59:25–59
Capozza DR, Van Order R (1980) Unique equilibria, pure profits, and efficiency in location models. Am Econ Rev 70:1046–1053
d’Aspremont C, Gabszewicz JJ, Thisse J-F (1979) On Hotelling’s ‘stability in competition’. Econometrica 47:1145–1150
DeGraba PJ (1987) The effects of price restrictions on competition between national and local firms. Rand J Econ 18:333–347
de Palma A, Ginsburgh Y, Papageorgiou YY, Thisse J-F (1985) The principle of minimum differentiation holds under sufficient heterogeneity. Econometrica 53:767–781
Eaton BC, Wooders MH (1985) Sophisticated entry in a model of spatial competition. Rand J Econ 16:282–297
Economides N (1986) Minimal and maximal product differentiation in Hotelling’s duopoly. Econ Lett 21:67–71
Economides N (1989) Symmetric equilibrium existence and optimality in differentiated product markets. J Econ Theory 47:178–194
Economides N (1993) Hotelling’s ‘main street’ with more than two competitors. J Reg Sci 33:303–319
Egger H, Egger P (2010) The trade and welfare effects of mergers in space. Reg Sci Urban Econ 40:210–220
Fik TJ (1991) Price competition and node-linkage association. Pap Reg Sci 70:53–69
Fik TJ, Mulligan GF (1991) Spatial price competition: a network approach. Geogr Anal 23:79–89
Fujita M, Thisse J-F (2002) Economics of agglomeration: cities, industrial location, and regional growth. Cambridge University Press, Cambridge
Gupta B (1992) Sequential entry and deterrence with competitive spatial price discrimination. Econ Lett 38:487–490
Hamilton JH, Thisse J-F, Weskamp A (1989) Spatial discrimination: Bertrand versus Cournot in a model of location choice. Reg Sci Urban Econ 19:87–102
Heywood JS, Ye G (2009) Mixed oligopoly and spatial price discrimination with foreign firms. Reg Sci Urban Econ 39:592–601
Hoover EM (1937) Spatial price discrimination. Rev Econ Stud 4:182–191
Hotelling H (1929) Stability in competition. Econ J 39:41–57
Hsu S-K (1983) Pricing in an urban spatial monopoly: a general analysis. J Reg Sci 23:165–175
Hurter AP, Lederer PJ (1985) Spatial duopoly with discriminatory pricing. Reg Sci Urban Econ 15:541–553
Lambertini L (1994) Equilibrium locations in the unconstrained Hotelling game. Econ Notes 23:438–446
Lambertini L (1997) Unicity of the equilibrium in the unconstrained Hotelling model. Reg Sci Urban Econ 27:785–798
Lederer PJ, Hurter AP (1986) Competition of firms: discriminatory pricing and location. Econometrica 54:623–640
Lerner A, Singer H (1937) Some notes on duopoly and spatial competition. J Political Econ 45:145–186
MacLeod B, Norman G, Thisse J-F (1988) Price discrimination and equilibrium in monopolistic competition. Int J Ind Organ 6:429–446
Matsumura T, Matsushima N (2009) Cost differentials and mixed strategy equilibria in a Hotelling model. Ann Reg Sci 43:215–234
Meza S, Tombak M (2009) Endogenous location leadership. Int J Ind Organ 27:687–707
Mulligan GF (1996) Myopic spatial competition: boundary effects and network solutions. Pap Reg Sci 75:155–176
Neven DJ (1987) Endogenous sequential entry in a spatial model. Int J Ind Organ 5:419–434
Osborne MJ, Pitchik C (1987) Equilibrium in Hotelling’s model of spatial competition. Econometrica 55:911–922
Salop SC (1979) Monopolistic competition with outside goods. Bell J Econ 10:141–156
Tabuchi T, Thisse J-F (1995) Asymmetric equilibria in spatial competition. Int J Ind Organ 13:213–227
Vickrey WS (1964) Microstatics. Harcourt, Brace and World, New York
Vickrey WS (1999) Spatial competition, monopolistic competition, and optimum product diversity. Int J Ind Organ 17:953–963
Yu C-M (2007) Price and quantity competition yield the same location equilibria in a circular market. Pap Reg Sci 86:643–655
Acknowledgments
I would like to thank two anonymous referees for helpful comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
In this “Appendix”, condensed from one in the previous version of the paper, I consider the validity of the Bertrand-Nash equilibrium in mill prices in Sect. 3, and then the validity of the subgame-perfect Nash equilibrium in locations in Sect. 4. I focus on the case \(n = 4\), but in the next paragraph I consider \(n = 2\), and at the end I consider \(n>4\). Differences from the model in DeGraba (1987), in addition to those mentioned in Sect. 5, are discussed below.
It is well known that everything is fine in the case \(n = 2\) (this is a special case of Caplin and Nalebuff 1991). It is very helpful that the demand curve for store 1 (and each other store) as a function of its own price is a straight line all the way from its vertical intercept to its horizontal intercept, even in cases where (for example) store 0 (in the middle) sells to some consumers to the left of store 1, or where store 1 sells to all consumers to the left of and some to the right of store 0. As will be seen below, the demand curve facing a store can be more complicated if \(n>2\).
Suppose now that \(n = 4\), which is the case of primary interest in this paper. The revenues (and profits) of store 0, as a function of the prices of all stores and the locations of the four peripheral stores, are given by substituting \(n = 4\) into (3).
Substituting \(n = 4\) into (5), we have \(2(3a + b)P_{0} - bP_{1}-3aP_{2} = tab(3b + a)\). From this equation and Eqs. (7) and (9), the following Bertrand-Nash equilibrium mill price functions are derived.
Since (20) is a strictly concave function of \(P_{0}\), (6) is a strictly concave function of \(P_{1}\), and (8) is a strictly concave function of \(P_{2}\), the (local) second-order conditions are satisfied for all stores if they are choosing the prices (21)–(23).
According to (15) with \(n = 4\), the Nash equilibrium values of a and b are \(a = b = 5/9\). I now fix b at 5/9 and check whether (or not) a pure-strategy Bertrand-Nash equilibrium in mill prices exists for various values of a in the unit interval [0, 1] that are not necessarily equal to 5/9.
The number of consumers served by store 1 is given by \(1 -z_{1}\), which equals the term in square brackets in (6) (since \(z_{1}\) is given by (1)), which yields the equation.
This is a linear function of \(P_{1}\), and thus (ignoring the complication described in the next paragraph for the time being), the profits of store 1 as a function of its own price would seem to be a strictly concave function, from the vertical intercept (the value of \(P_{1}\) for which the number of consumers is 0) down to the horizontal intercept (\(P_{1}= 0\)), for any value of a, given that \(b = 5/9\).
The complicating feature of the analysis is that, with some values of a, and with b fixed at 5/9, there may be a positive value of \(P_{1}\) for which (24) gives \(1 - z_{1} = 1\) (or \(z_{1} = 0\)), so the market area of store 1 is the line segment it is located on, but no more. I denote this value of \(P_{1}\) by \(P_{1u}(a, b, n)\) for general values of b and n, and by \(P_{1u}\)(a, 5/9, 4) for the case here. In DeGraba (1987), for any value of n (including his main case \(n = 2\), and the case \(n>2\) in his extensions section), the demand curve is continuous, but it has a kink and becomes vertical for prices below this (from \(P_{1} =P_{1u}(a, b, n)\) down to \(P_{1}= 0)\), since the quantity demanded from a local firm can never be greater than 1 in his model. In my model, something very different happens for some values of a. For \(n = 4\) and \(b = 5/9\), and if \(0\le P_{1}<P_{1u}(a, 5/9, 4)\), then \(z_{1} < 0\), so the profits of store 1 are no longer given by \(\pi _{1} = (1 - z_{1})P_{1}\), which is the formula in the text just before (6), and thus are no longer given by (6). Whenever \(z_{1} < 0\), store 1 sells to all consumers on its own segment of length 1, plus consumers in [\(0, z_{1}\)] on each of the other three segments. There is a kink in the demand curve for store 1 at this price, and, for \(P_{1} <P_{1u}(a, 5/9, 4)\), demand is only 1/3 as steep as it is for higher prices. It is possible (see Appendix of previous version of paper) to derive the equation \(2P_{1}- P_{0} = ta[(2/3) - a]\). Assuming \(P_{0}\) is fixed at its equilibrium value, given by (22), this is easily solved for \(P_{1}= P_{1v}(a, 5/9, 4)\), the profit-maximizing price for store 1 if store 1 is on this low-price segment of the demand curve. A similar complication exists for any \(n>2\). Note the difference between DeGraba 1987, where (as pointed out above) there is a “downward kink” for any value of n, and my model, where there is an “upward kink” if \(n>2\).
If \(a = b = 5/9\), then, using (21), (22), \(P_{1} = P_{1}(5/9, 5/9, 4) = (155/243)(t)\) and \(P_{0} = P_{0}(5/9, 5/9, 4) = (115/243)(t)\), in agreement with Proposition 3. As \(P_{1}\) decreases, starting from \(P_{1}(5/9, 5/9, 4)\), the profits of store 1 decrease monotonically to 0 at \(P_{1}= 0\), so store 1 maximizes its profits by choosing \(P_{1}= P_{1}(5/9, 5/9, 4) = (155/243)(t)\). Everything works out nicely, and the Bertrand-Nash equilibrium in prices described by (21)–(23) is exactly correct.
Suppose now that \(a = 1/3\) (and \(b = 5/9\)). It can be shown (see Appendix of previous version of paper) that everything works out nicely (just as it did when \(a = 5/9\)), and once again the Bertrand-Nash equilibrium in prices described by (21)–(23) is exactly correct.
However, suppose that \(a = 2/9\). It can be shown (see Appendix of previous version of paper) that store 1 reaches its maximum profits, for the given location pattern (and for the given \(P_{0})\), by choosing \(P_{1}= P_{1v}(2/9, 5/9, 4)\). In this case, therefore, things do not work out neatly, and the pure-strategy Bertrand-Nash equilibrium in prices described by (21)–(23) is not valid.
More generally, for \(n = 4\), and with three of the peripheral stores at their equilibrium locations (\(b = 5/9\)), the Bertrand-Nash equilibrium in mill prices described in Sect. 3, and by (21)–(23), is valid if the distance of store 1 from the central intersection is \(a>a^{*}\), but not if \(a<a^{*}\), for some \(a^{*}\) such that \(2/9<a^{*}<1/3\). In fact, \(a^{*}\) is just very slightly greater than 1/4.
Consider existence of a subgame-perfect Nash equilibrium. Anderson (1988) states what must be shown for the simpler case of spatial duopoly. First, I confine attention to pure strategies (see pp. 480, 482, and fn. 2 of Anderson 1988). In my model with \(n = 4\), in order to show that the set of locations stated in Proposition 3 (\(a = b = 5/9\)) is a part of a pure-strategy subgame-perfect Nash equilibrium, it is necessary to show that if three of the peripheral stores are at their equilibrium locations, \(b = 5/9\), then a pure-strategy Bertrand-Nash equilibrium in mill prices exists for any location of store 1 (i.e., for any value of a in the interval [0, 1]) and that the resultant profits of store 1 are higher if \(a = 5/9\) than for any other value of a in [0, 1]. However, in my model with \(n = 4,\) this works only if the location space for each peripheral store is restricted to [\(a^{*}, 1\)], where \(a^{*}\approx 1/4,\) because only for these values of a does a pure-strategy Bertrand-Nash equilibrium in mill prices exist (given that \(b = 5/9\)), as discussed above.
Some spatial duopoly models (Osborne and Pitchik (1987); Anderson (1988)) consider “the case when the strategy space is enlarged to include mixed strategies at the price stage” (Anderson 1988, p. 480). (Anderson (1988), p. 490) states “as long as the mixed-strategy price equilibrium is unique in terms of payoffs, the location game is now well defined. If there is an equilibrium to this game, it may well be such that mixed strategies are never played at equilibrium.” The second sentence applies to my model for \(n = 4\), since at \(a = b = 5/9\) there is a pure-strategy Nash equilibrium in prices. I have not derived mixed-strategy Nash equilibria in prices when \(b = 5/9\) and \(0<a <a^{*}\). As observed by (Anderson (1988), p. 489), Osborne and Pitchik (1987) have solved their case only by using very complicated computer simulations. Their equilibrium locations are in the region where there is no pure-strategy Nash equilibrium in prices. In my case with \(n = 4\), and with \(b = 5/9\), it is only if a is much less than 5/9 that it is necessary to resort to mixed-strategy price equilibria, and the mixed-strategy profits of store 1 for these values of a are almost certainly much less than the pure-strategy equilibrium profits when \(a = 5/9\). If this is indeed true, then if mixed-price strategies are allowed, the subgame-perfect Nash equilibrium in Proposition 3 (with \(a = b = 5/9\)) is valid if the location space for each peripheral store is the whole interval [0, 1].
Consider \(n>4\). For a sufficiently large \(n\), and for the equilibrium value of \(b\), given by (15), a pure-strategy Bertrand-Nash equilibrium in prices might fail to exist even if a assumes its equilibrium value, given by (15). In fact, this is almost certainly the case in the limit that \(n\) goes to infinity, which is the case considered in Proposition 4. However (see Appendix of previous version of paper) this potential problem does not exist at all with the model in footnote 7.