Abstract
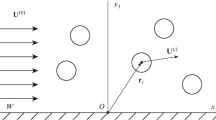
The motion of a heavy finite-size tracer is numerically calculated in a two-dimensional shear-driven cavity. The particle motion is computed using a discontinuous Galerkin-finite-element method combined with a smoothed profile method resolving all scales, including the flow in the lubrication gap between the particle and the boundary. The centrifugation of heavy particles in the recirculating flow is counteracted by a repulsion from the shear-stress surface. The resulting limit cycle for the particle motion represents an attractor for particles in dilute suspensions. The limit cycles obtained by fully resolved simulations as a function of the particle size and density are compared with those obtained by one-way coupling using the Maxey–Riley equation and an inelastic collision model for the particle–boundary interaction, solely characterized by an interaction-length parameter. It is shown that the one-way coupling approach can faithfully approximate the true limit cycle if the interaction length is selected depending on the particle size and its relative density.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
References
Brenner, C.E.: Fundamentals of Multiphase Flow. Cambridge University Press, Cambridge (2005)
Geurts, B.J., Clercx, H., Uijttewaal, W. (eds.): Particle-Laden Flow: From Geophysical to Kolmogorov Scales. Springer, Berlin (2007)
Crowe, C.T., Schwarzkopf, J.D., Sommerfeld, M., Tsuji, Y.: Multiphase Flows with Droplets and Particles. CRC Press, Boca Raton (2011)
Seetharaman, S.: Treatise on Process Metallurgy Process Phenomena. Elsevier, Amsterdam (2013)
Liu, L., Zheng, H., Williams, L., Zhang, F., Wang, R., Hertzberg, J., Shandas, R.: Development of a custom-designed echo particle image velocimetry system for multi-component hemodynamic measurements: system characterization and initial experimental results. Phys. Med. Biol. 53, 1397 (2008)
Merzkirch, W.: Flow Visualization. Elsevier, Amsterdam (2012)
Muldoon, F.H., Kuhlmann, H.C.: Coherent particulate structures by boundary interaction of small particles in confined periodic flows. Phys. D 253, 40 (2013)
de Motta, J.C.B., Breugem, W.P., Gazanion, B., Estivalezes, J.L., Vincent, S., Climent, E.: Numerical modelling of finite-size particle collisions in a viscous fluid. Phys. Fluids 25, 083302 (2013)
Lecoq, N., Anthore, R., Cichocki, B., Szymczak, P., Feuillebois, F.: Drag force on a sphere moving towards a corrugated wall. J. Fluid Mech. 513, 247 (2004)
Tan, J., Luo, K., Fan, J.: Three-dimensional particle-resolved direct numerical simulation study of behaviors of a particle settling near a vertical wall. Powder Technol. 275, 290 (2015)
Swan, J.W., Brady, J.F.: Particle motion between parallel walls: hydrodynamics and simulation. Phys. Fluids 22, 103301 (2010)
Breugem, W.P.: A second-order accurate immersed boundary method for fully resolved simulations of particle-laden flows. J. Comput. Phys. 231, 4469 (2012)
Nakayama, Y., Kim, K., Yamamoto, R.: Direct simulation of flowing colloidal dispersions by smoothed profile method. Adv. Powder Technol. 21, 206 (2010)
Yamamoto, R., Nakayama, Y., Kim, K.: A method to resolve hydrodynamic interactions in colloidal dispersions. Comput. Phys. Commun. 169, 301 (2005)
Costa, P., Boersma, B.J., Westerweel, J., Breugem, W.P.: Collision model for fully resolved simulations of flows laden with finite-size particles. Phys. Rev. E 92, 053012 (2015)
Hofmann, E., Kuhlmann, H.C.: Particle accumulation on periodic orbits by repeated free surface collisions. Phys. Fluids 23, 072106 (2011)
Mukin, R.V., Kuhlmann, H.C.: Topology of hydrothermal waves in liquid bridges and dissipative structures of transported particles. Phys. Rev. E 88, 053016 (2013)
Kuhlmann, H.C.: Thermocapillary Convection in Models of Crystal Growth. Springer, Berlin (1999)
Schwabe, D., Tanaka, S., Mizev, A., Kawamura, H.: Particle accumulation structures in time-dependent thermocapillary flow in a liquid bridge under microgravity conditions. Microgravity Sci. Technol. 18, 117 (2006)
Nakayama, Y., Yamamoto, R.: Simulation method to resolve hydrodynamic interactions in colloidal dispersions. Phys. Rev. E 71, 036707 (2005)
Nakayama, Y., Kim, K., Yamamoto, R.: Hydrodynamic effects in colloidal dispersions studied by a new efficient direct simulation. Flow Dyn. 832, 245 (2006)
Yamamoto, R., Kim, K., Nakayama, Y.: Strict simulations of non-equilibrium dynamics of colloids. Colloid Surf. A 311, 42 (2007)
Jafari, S., Yamamoto, R., Rahnama, M.: Lattice-Boltzmann method combined with smoothed-profile method for particulate suspensions. Phys. Rev. E 83, 026702 (2011)
Kim, K., Nakayama, Y., Yamamoto, R.: A smoothed profile method for simulating charged colloidal dispersions. Comput. Phys. Commun. 169, 104 (2005)
Kim, K., Yamamoto, R.: Efficient simulations of charged colloidal dispersions: a density functional approach. Macromol. Theor. Simul. 14, 278 (2005)
Kim, K., Nakayama, Y., Yamamoto, R.: Direct numerical simulations of electrophoresis of charged colloids. Phys. Rev. Lett. 96, 208302 (2006)
Nakayama, Y., Kim, K., Yamamoto, R.: Simulating (electro) hydrodynamic effects in colloidal dispersions: smoothed profile method. Eur. Phys. J. E 26, 361 (2008)
Yamamoto, R., Nakayama, Y., Kim, K.: Smoothed profile method to simulate colloidal particles in complex fluids. Int. J. Mod. Phys. C 20, 1457 (2009)
Luo, X., Beskok, A., Karniadakis, G.E.: Modeling electrokinetic flows by the smoothed profile method. J. Comput. Phys. 229, 3828 (2010)
Kang, S., Suh, Y.K.: Direct simulation of flows with suspended paramagnetic particles using one-stage smoothed profile method. J. Fluid Struct. 27, 266 (2011)
Hesthaven, J.S., Warburton, T.: Nodal Discontinuous Galerkin Methods: Algorithms, Analysis, and Applications. Springer, Berlin (2007)
Luo, X., Maxey, M.R., Karniadakis, G.E.: Smoothed profile method for particulate flows: error analysis and simulations. J. Comput. Phys. 228, 1750 (2009)
Romanò, F., Kuhlmann, H.C.: Smoothed profile method for momentum and heat transfer in particulate flows. Int. J. Numer. Methods Fluids 83, 485 (2017)
Karniadakis, G.E., Israeli, M., Orszag, S.A.: High-order splitting methods for the incompressible Navier–Stokes equations. J. Comput. Phys. 97, 414 (1991)
Maxey, M.R., Riley, J.J.: Equation of motion for a small rigid sphere in a nonuniform flow. Phys. Fluids 26, 883 (1983)
Taylor, G.I., Green, A.E.: Mechanism of the production of small eddies from large ones. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 158, 499 (1937)
Domesi, S., Kuhlmann, H.C.: PAS project report 2002. Tech. rep., ZARM (2002)
Romanò, F., Kuhlmann, H.C.: Numerical investigation of the interaction of a finite-size particle with a tangentially moving boundary. Int. J. Heat Fluid Flow 62, 75 (2016)
Schwabe, D., Frank, S.: Particle accumulation structures (PAS) in the toroidal thermocapillary vortex of a floating-zone model for a step in planet formation? Adv. Space Res. 23, 1191 (1999)
Brenner, H.: The slow motion of a sphere through a viscous fluid towards a plane surface. Chem. Eng. Sci. 16, 242 (1961)
Acknowledgements
Open access funding provided by TU Wien (TUW).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by S. Balachandar.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Romanò, F., Kuhlmann, H.C. Particle–boundary interaction in a shear-driven cavity flow. Theor. Comput. Fluid Dyn. 31, 427–445 (2017). https://doi.org/10.1007/s00162-017-0430-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00162-017-0430-4