Skip to main content
SpringerLink
Log in

Long-lasting effect of initial configuration in gravitational spreading of material fronts

  • Original Article
  • Published:
Theoretical and Computational Fluid Dynamics Aims and scope Submit manuscript

Abstract

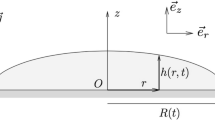
We present the results from laboratory experiments and fully resolved simulations pertaining to finite-release turbulent density flows with a non-axisymmetric initial shape. First, we demonstrate that the effects of the initial shape influence the current’s evolution well into the long-time phase which would corresponds to the inertial self-similar phase in the case of planar or axisymmetric configurations. Then, we identify the physical mechanisms responsible for this dependence and propose a new model capable of capturing the dynamics of such releases. Finally, we show that this dependence on the initial configuration is robust for various types of gravity currents over a wide range of parameters such as Reynolds number, density ratio, and aspect ratio.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Hoult D.P.: Oil spreading in the sea. Annu. Rev. Fluid Mech. 4, 341 (1972)

    Article  Google Scholar 

  2. Britter R.E.: Atmospheric dispersion of dense gases. Annu. Rev. Fluid Mech. 21, 317 (1989)

    Article  Google Scholar 

  3. Gröbelbauer H.P., Fanneløp T.K., Britter R.E.: The propagation of intrusion fronts of high density ratio. J. Fluid Mech. 250, 669 (1993)

    Article  Google Scholar 

  4. Doyle J., Carlson J.M.: Power laws, highly optimized tolerance, and generalized source coding. Phys. Rev. Lett. 84, 5656 (2000)

    Article  Google Scholar 

  5. Meiburg E., Kneller B.: Turbidity currents and their deposits. Annu. Rev. Fluid Mech. 42, 135 (2010)

    Article  Google Scholar 

  6. Faillettaz J., Louchet F., Grasso J.R.: Two-threshold model for scaling laws of noninteracting snow avalanches. Phys. Rev. Lett. 93, 208001 (2004)

    Article  Google Scholar 

  7. Hopfinger E.J.: Snow avalanche motion and related phenomena. Annu. Rev. Fluid Mech. 15, 47 (1983)

    Article  Google Scholar 

  8. Hall F.F., Neff W.D., Frazier T.V.: Wind shear observations in thunderstorm density currents. Nature 264, 408 (1976)

    Article  Google Scholar 

  9. Simpson J.E.: Gravity currents in the laboratory, atmosphere and oceans. Annu. Rev. Fluid Mech. 14, 213 (1982)

    Article  Google Scholar 

  10. Huppert H.E.: Gravity currents: a personal perspective. J. Fluid Mech. 554, 299 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  11. von Karman R.: The engineer grapples with nonlinear problems. Bull. Am. Math. Soc. 46, 615 (1940)

    Article  Google Scholar 

  12. Benjamin T.B.: Density currents and related phenomena. J. Fluid Mech. 31, 209 (1968)

    Article  MATH  Google Scholar 

  13. Hallworth M.A., Huppert H.E., Ungarish M.: Axisymmetric gravity currents in a rotating system: experimental and numerical investigations. J. Fluid Mech. 447, 1 (2001)

    Article  MATH  Google Scholar 

  14. Huq P.: The role of aspect ratio on entrainment rates of instantaneous, axisymmetric finite volume releases of density fluid. J. Hazard. Mater. 49, 89 (1996)

    Article  Google Scholar 

  15. Huppert H.E., Simpson J.E.: The slumping of gravity currents. J. Fluid Mech. 99, 785 (1980)

    Article  Google Scholar 

  16. Cantero M., Lee J., Balachandar S., García M.: On the front velocity of gravity currents. J. Fluid Mech. 586, 1 (2007)

    Article  MATH  Google Scholar 

  17. Zemach T., Ungarish M.: Gravity currents in non-rectangular cross-section channels: analytical and numerical solutions of the one-layer shallow-water model for high-Reynolds-number propagation. Phys. Fluids 25, 026601 (2013)

    Article  Google Scholar 

  18. Rottman J.W., Simpson J.E.: Density currents produced by instantaneous releases of a heavy fluid in a rectangular channel. J. Fluid Mech. 135, 95 (1983)

    Article  Google Scholar 

  19. Klemp J.B., Rotunno R., Skamarock W.C.: On the dynamics of density currents in a channel. J. Fluid Mech. 269, 169 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  20. Cantero M., Balachandar S., García M., Bock D.: Turbulent structures in planar gravity currents and their influence on the flow dynamics. J. Geophys. Res. Oceans 113, C08018 (2008)

    Article  Google Scholar 

  21. Lighthill J.: Waves in Fluids. Cambridge University Press, Cambridge (1978)

    MATH  Google Scholar 

  22. Sachdev P.L.: Shock Waves and Explosions. Chapman & Hall/CRC, London (2004)

    Book  MATH  Google Scholar 

  23. Ungarish M.: An Introduction to Gravity Currents and Intrusions. CRC Press, Boca Raton (2009)

    Book  MATH  Google Scholar 

  24. Cantero M., Balachandar S., Garcia M.: High-resolution simulations of cylindrical density currents. J. Fluid Mech. 590, 437 (2007)

    Article  MATH  Google Scholar 

  25. Simpson J.E.: Effect of the lower boundary on the head of a gravity current. J. Fluid Mech. 53, 759 (1972)

    Article  Google Scholar 

  26. La Rocca M., Adduce C., Sciortino G., Pinzon A.B.: Experimental and numerical simulation of three-dimensional gravity currents on smooth and rough bottom. Phys. Fluids 20, 106603 (2008)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical and Aerospace Engineering, University of Florida, Gainesville, FL, 32611, USA

    Nadim Zgheib & S. Balachandar

  2. Université de Toulouse, INPT, UPS, UMR 552, IMFT, Allée Camille Soula, 31400, Toulouse, France

    Nadim Zgheib & Thomas Bonometti

  3. CNRS, IMFT, 31400, Toulouse, France

    Thomas Bonometti

Authors
  1. Nadim Zgheib
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Thomas Bonometti
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. S. Balachandar
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Thomas Bonometti.

Additional information

Communicated by Tim Colonius.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zgheib, N., Bonometti, T. & Balachandar, S. Long-lasting effect of initial configuration in gravitational spreading of material fronts. Theor. Comput. Fluid Dyn. 28, 521–529 (2014). https://doi.org/10.1007/s00162-014-0330-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00162-014-0330-9

Keywords

Search

Navigation