Skip to main content

Advertisement

SpringerLink
Log in

A simple equilibrium model for shallow-cumulus-topped mixed layers

  • Original Article
  • Published:
Theoretical and Computational Fluid Dynamics Aims and scope Submit manuscript

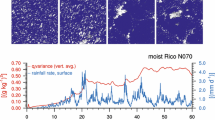
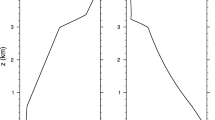
Abstract

A new equilibrium model for shallow-cumulus-topped mixed layers is presented. A variant on the w * closure for the shallow-cumulus mass flux is applied that retains the convective area-fraction in its formulation. As opposed to being constant, the fraction is explicitly modeled using a statistical closure as a function of the saturation deficit and humidity variance at cloud base. As a consequence, important new interactions are introduced between the convective transport, humidity, and depth of the mixed layer. This mechanism, which we call the mass-flux humidity feedback, helps determine the character of the equilibrium state such that the mixed-layer top is maintained close to the cloud-base height. Due to the strong sensitivity of the mass flux to the area fraction, the latter thus acts as a regulator or valve mechanism on moist convective transport. As a consequence, the mixed-layer model is able to explain the robustness of many aspects of the shallow-cumulus boundary layer that is typically found in observations and large-eddy simulations (LESs). The model is evaluated for a single-LES case as well as for global climatology obtained from a 40-year reanalysis of meteorological data by the European Centre for Medium-range Weather Forecasts (ECMWF). LES characteristics of convective mass flux, cloud fraction, humidity variance, cloud-base height, and surface fluxes of heat and humidity are reproduced. The solution on reanalysis fields reproduces the spatial structure of mixed-layer temperature and humidity and their associated surface fluxes in the subtropical Atlantic and Pacific trade wind regions. Furthermore, the spatial structure of the convective area-fraction matches that of synoptic surface observations of frequency of occurrence of shallow cumulus. Particularly striking is the smooth onset of the convective area-fraction and mass flux along the trade-wind trajectory that is reproduced, from zero to typical trade-wind values. The cumulus onset represents the necessity for shallow-cumulus mass flux to occur in order to close the mixed-layer budgets of heat, moisture, and mass, as a response to the changing magnitude of large-scale subsidence and free tropospheric humidity along the trajectory. Finally, the mass flux model is implemented in an intermediate-complexity tropical climate model to study its behavior when fully interactive with the larger-scale flow. A climate run then shows that the model is stable, due to the mass-flux humidity feedback acting to keep the shallow-cumulus boundary layer close to its equilibrium state for long, climatological timescales.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Albrecht B.A., Betts A.K., Schubert W.H., Cox S.K. (1979): A model of the thermodynamic structure of the Trade-wind boundary layer. Part I: Theoretical formulation and sensitivity tests. J. Atmos. Sci. 36, 73–89

    Article  ADS  Google Scholar 

  2. Albrecht B.A., Bretherton C.S., Johnson D., Schubert W.H., Frisch A.S. (1995): The Atlantic stratocumulus transition experiment—ASTEX. Bull. Am. Meteorol. Soc. 76, 889–904

    Article  ADS  Google Scholar 

  3. Anthes R.A., Keyser D. (1979): Tests of a fine-mesh model over Europe and the United States. Mon. Wea. Rev. 107, 963–984

    Article  Google Scholar 

  4. Augstein E., Riehl H., Ostapoff F., Wagner V. (1973): Mass and energy transports in an undisturbed Atlantic trade-wind flow. Mon. Wea. Rev. 101, 101–111

    Google Scholar 

  5. Augstein E., Schmidt H., Wagner V. (1974): The vertical structure of the atmospheric planetary boundary layer in undisturbed Trade winds over the Atlantic Ocean. Bound. Layer Meteorol. 6, 129–150

    Article  ADS  Google Scholar 

  6. Berg L.K., Stull R.B. (2004): Parameterization of joint frequency distributions of potential temperature and water vapor mixing ratio in the daytime convective boundary layer. J. Atmos. Sci. 61, 813–828

    Article  ADS  Google Scholar 

  7. Betts A.K. (1973): Non-precipitating cumulus convection and its parameterization. Q. J. R. Meteorol. Soc. 99, 178–196

    Article  ADS  Google Scholar 

  8. Betts A.K. (1976): Modeling subcloud layer structure and interaction with a shallow cumulus layer. J. Atmos. Sci. 33, 2363–2382

    Google Scholar 

  9. Betts A.K., Ridgway W. (1989): Climatic equilibrium of the atmospheric convective boundary layer over the tropical ocean. J. Atmos. Sci. 46, 2621–2641

    Article  ADS  Google Scholar 

  10. Bretherton C.S., Wyant M.C. (1997): Moisture transport, lower-tropospheric stability, and decoupling of cloud-topped boundary layers. J. Atmos. Sci. 54, 148–167

    Article  ADS  Google Scholar 

  11. Bretherton C.S., McCaa J.R., Grenier H. (2004): A new parameterization for shallow cumulus convection and its application to marine subtropical cloud-topped boundary layers. Part I: description and 1D results. Mon. Wea. Rev. 132, 864–882

    Article  Google Scholar 

  12. Brown A.R., Chlond A., Golaz C., Khairoutdinov M., Lewellen D.C., Lock A.P., MacVean M.K. Moeng C-H., Neggers R.A.J., Siebesma A.P., Stevens B. (2002): Large-eddy simulation of the diurnal cycle of shallow cumulus convection over land. Q. J. R. Meteorol. Soc. 128, 1075–1094

    Article  ADS  Google Scholar 

  13. Cheinet S. (2004): A multiple mass flux parameterization for the surface-generated convection. Part II: Cloudy cores. J. Atmos. Sci. 61, 1093–1113

    Article  ADS  Google Scholar 

  14. Cuijpers H., Duynkerke P.G. (1993): Large-eddy simulation of trade-wind cumulus clouds. J. Atmos. Sci. 50, 3894–3908

    Article  ADS  Google Scholar 

  15. Cuijpers H., Bechtold P. (1995): A simple parameterization of cloud water related variables for use in boundary layer models. J. Atmos. Sci. 52, 2486–2490

    Article  ADS  Google Scholar 

  16. Deardorff J.W. (1970): Convective velocity and temperature scales for the unstable planetary boundary layer and for Rayleigh convection. J. Atmos. Sci. 27, 1211–1212

    Article  ADS  Google Scholar 

  17. Garratt J.R. (1977): Review of drag coefficients over oceans and continents. Mon. Wea. Rev. 105, 915–929

    Article  Google Scholar 

  18. Grant A.L.M. (2001): Cloud-base fluxes in the cumulus-capped boundary layer. Q. J. Roy. Meteorol. Soc. 127, 407–422

    Article  ADS  Google Scholar 

  19. Grant A.L.M., Brown A.R. (1999): A similarity hypothesis for shallow-cumulus transports. Q. J. R. Meteorol. Soc. 125, 1913–1936

    Article  ADS  Google Scholar 

  20. Holland J.Z., Rasmusson E.M. (1973): Measurement of atmospheric mass, energy and momentum budgets over a 500-kilometer square of tropical ocean. Mon. Wea. Rev. 101, 44–55

    Google Scholar 

  21. Lenderink G., Siebesma P., Cheinet S., Irons S., Jones C.G., Marquet P., Müller F., Olmeda D., Calvo J., Sanchez E., Soares P.M.M. (2004): The diurnal cycle of shallow cumulus clouds over land: a single column model intercomparison study. Q. J. R. Meteorol. Soc. 130, 3339–3364

    Article  ADS  Google Scholar 

  22. Lilly D.K. (1968): Models of cloud-topped mixed layers under a strong inversion. Q. J. R. Meteorol. Soc. 84, 292–309

    Google Scholar 

  23. Neelin J.D., Zeng N. (2000): A quasi-equilibrium tropical circulation model–formulation. J. Atmos. Sci. 57, 1741–1766

    Article  ADS  Google Scholar 

  24. Neggers R.A.J., Siebesma A.P., Lenderink G., Holtslag A.A.M. (2004): An evaluation of mass flux closures for diurnal cycles of shallow cumulus. Mon. Wea. Rev. 132, 2525–2538

    Article  Google Scholar 

  25. Neggers, R.A.J., Stevens, B., Neelin, J.D.: Variance scaling in shallow cumulus topped mixed layers. Q. J. R. Meteorol. Soc. August 2006 (submitted)

  26. Neggers, R.A.J., Neelin, J.D., Stevens, B.: Impact mechanisms of shallow cumulus convection on tropical climate dynamics. J. Clim. July 2006 (accepted pending minor revisions)

  27. Nicholls S., LeMone M.A. (1980): The fair weather boundary layer in GATE: the relationship of subcloud fluxes and structure to the distribution and enhancement of cumulus clouds. J. Atmos. Sci. 37, 2051–2067

    Article  ADS  Google Scholar 

  28. Nitta T., Esbensen S. (1974): Heat and moisture budget analyses using BOMEX data. Mon. Wea. Rev. 102, 17–28

    Article  Google Scholar 

  29. Norris J.R. (1998): Low cloud type over the ocean from surface observations. Part II: geographical and seasonal variations. J. Clim. 11, 383–403

    Article  ADS  Google Scholar 

  30. Ooyama K. (1971): A theory on parameterization of cumulus convection. J. Meteorol. Soc. Jpn. 49, 744–756

    Google Scholar 

  31. Riehl H., Yeh C., Malkus J.S., LaSeur N.E. (1951): The northeast trade of the Pacific Ocean. Q. J. R. Meteor. Soc. 77, 598–626

    Google Scholar 

  32. Schubert W.H. (1976): Experiments with Lilly’s cloud-topped mixed layer model. J. Atmos. Sci. 33, 436–446

    Article  ADS  Google Scholar 

  33. Siebesma A.P., Cuijpers (1995): Evaluation of parametric assumptions for shallow cumulus convection. J. Atmos. Sci. 52, 650–666

    Article  ADS  Google Scholar 

  34. Siebesma A.P., Bretherton C.S., Brown A., Chlond A., Cuxart J., Duynkerke P.G., Jiang H., Khairoutdinov M., Lewellen D., Moeng C.-H., Sanchez E., Stevens B., Stevens D.E. (2003): A large eddy simulation intercomparison study of shallow cumulus convection. J. Atmos. Sci. 60, 1201–1219

    Article  ADS  Google Scholar 

  35. Siebesma A.P., Jakob C., Lenderink G., Neggers R.A.J., Teixeira J., Van Meijgaard E., Calvo J., Chlond A., Grenier H., Jones C., Koehler M., Kitagawa H., Marquet P., Lock A.P., Muller F., Olmeda D., Severijns C. (2004): Cloud representation in general-circulation models over the northern Pacific Ocean: a EUROCS intercomparison study. Q. J. R. Meteorol. Soc. 130, 1–23

    Article  Google Scholar 

  36. Sommeria G., Deardorff J.W. (1977): Subgrid-scale condensation in models of non-precipitating clouds. J. Atmos. Sci. 34, 344–355

    Article  ADS  Google Scholar 

  37. Stevens, B.: Boundary layer concepts for simplified models of tropical dynamics. Theor. Comput. Fluid Dyn. (in press) (2006)

  38. Stevens B., Ackerman A.S., Albrecht B.A., Brown A.R., Chlond A., Cuxart J., Duynkerke P.G., Lewellen D.C., MacVean M.K., Neggers R.A.J., Sanchez E., Siebsema A.P., Stevens D.E. (2001): Simulations of Trade-wind cumuli under a strong inversion. J. Atmos. Sci. 58, 1870–1891

    Article  ADS  Google Scholar 

  39. Stull R.B. (1988): An introduction to boundary layer meteorology. Kluwer, Dordrecht

    MATH  Google Scholar 

  40. Yanai M., Esbensen S., Cho J.H. (1973): Determination of bulk properties of tropical cloud clusters from large-scale heat and moisture budgets. J. Atmos. Sci. 30, 611–627

    Article  ADS  Google Scholar 

  41. Yin B., Albrecht B.A. (2000): Spatial variability of atmospheric boundary layer structure over the eastern equatorial Pacific. J. Clim. 13, 1574–1592

    Article  ADS  Google Scholar 

Download references

Author information

Author notes

  1. Roel Neggers

    Present address: European Centre for Medium-range Weather Forecasts (ECMWF), Shinfield Park, Reading, Berkshire, RG2 9AX, UK

Authors and Affiliations

  1. Department of Atmospheric and Oceanic Sciences, University of California at Los Angeles (UCLA), Los Angeles, CA, USA

    Roel Neggers, Bjorn Stevens & J. David. Neelin

Authors
  1. Roel Neggers
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Bjorn Stevens
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. J. David. Neelin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Roel Neggers.

Additional information

Communicated by R. Klein.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Neggers, R., Stevens, B. & Neelin, J.D. A simple equilibrium model for shallow-cumulus-topped mixed layers. Theor. Comput. Fluid Dyn. 20, 305–322 (2006). https://doi.org/10.1007/s00162-006-0030-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00162-006-0030-1

Keywords

PACS

Search

Navigation