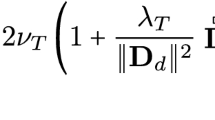Skip to main content
SpringerLink
Log in

An explicit algebraic Reynolds stress and heat flux model for incompressible turbulence: Part I Non-isothermal flow

  • Published:
Theoretical and Computational Fluid Dynamics Aims and scope Submit manuscript

Abstract

Tensor representation theory is used to derive an explicit algebraic model that consists of an explicit algebraic stress model (EASM) and an explicit algebraic heat flux model (EAHFM) for two-dimensional (2-D) incompressible non-isothermal turbulent flows. The representation methodology used for the heat flux vector is adapted from that used for the polynomial representation of the Reynolds stress anisotropy tensor. Since the methodology is based on the formation of invariants from either vector or tensor basis sets, it is possible to derive explicit polynomial vector expansions for the heat flux vector. The resulting EAHFM is necessarily coupled with the turbulent velocity field through an EASM for the Reynolds stress anisotropy. An EASM has previously been derived by Jongen and Gatski [10]. Therefore, it is used in conjunction with the derived EAHFM to form the explicit algebraic model for incompressible 2-D flows. This explicit algebraic model is analyzed and compared with previous formulations including its ability to approximate the commonly accepted value for the turbulent Prandtl number. The effect of pressure-scrambling vector model calibration on predictive performance is also assessed. Finally, the explicit algebraic model is validated against a 2-D homogeneous shear flow with a variety of thermal gradients.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Adumitroaie, V., Taulbee, D.B. and Givi, P.: Explicit algebraic scalar-flux models for turbulent reacting flows. AIChE Journal 43, 1935–1946 (1997)

  2. Corrsin, S.: Limitations of gradient transport models in random walks and in turbulence. Turbulent Diffusion in Environmental Pollution, Advances in Geophysics. F.N. Frenkiel, R.E. Munn (Eds.), Vol. 18A, pp. 25–60 (1974)

  3. Daly, B.J., Harlow, F.H.: Transport equations in turbulence. Physics of Fluids 13, 2634–2649 (1970)

  4. Gatski, T.B., Speziale, C.G.: On explicit algebraic stress models for complex turbulent flows. Journal of Fluid Mechanics 254, 59–78 (1993)

  5. Gatski, T.B., Jongen, T.: Nonlinear eddy viscosity and algebraic stress models for solving complex turbulent flows. Progress in Aerospace Science 36, 655–682 (2000)

  6. Gibson, M.M.: An algebraic stress and heat-flux model for turbulent shear flow with streamline curvature. International Journal of Heat and Mass Transfer 21, 1609–1617 (1978)

  7. Girimaji, S.S.: Fully explicit and self-consistent algebraic Reynolds stress model. Theoretical and Computational Fluid Dynamics 8, 387–402 (1996)

  8. Girimaji, S.S., Balachandar, S.: Analysis and modeling of buoyancy-generated turbulence using numerical data. International Journal of Heat and Mass Transfer 41, 915–929 (1998)

  9. Jones, W.P., Musonge, P.: Closure of the Reynolds-stress and scalar flux equations. Physics of Fluids 31, 3589–3604 (1988)

  10. Jongen, T., Gatski T.B.: General explicit algebraic stress relations and best approximation for three-dimensional flows. International Journal of Engineering Science 36, 739–763 (1998)

  11. Launder, B.E.: Heat and Mass Transfer. In Topics in Physics. P. Bradshaw (Ed.), pp. 231–287, Springer-Verlag, New York (1978)

  12. Mellor, G.L., Yamada, T.: A hierarchy of turbulence closure models for planetary boundary layers. Journal of Atmospheric Sciences 31, 1791–1806 (1974)

  13. Pope, S.B.: A more general effective viscosity hypothesis. Journal of Fluid Mechanics 72, 331-340 (1975)

  14. Rivlin, R.S., Ericksen, J.L.: Stress-deformation relations for isotropic materials. Archive of Rational Mechanics and Analysis 4, 323-425 (1955)

  15. Rodi, W.: The prediction of free turbulent boundary layers by use of a two equation model of turbulence. PhD thesis, University of London, London, UK (1972)

  16. Rodi, W.: A new algebraic relation for calculating the Reynolds stresses. ZAMM 56, 219–221 (1976)

  17. Rogers, M.M., Moin, P., Reynolds, W.C.: The structure and modeling of the hydrodynamic and passive scalar fields in homogeneous turbulent shear flow. Department of Mechanical Engineering. Report TF-25, Stanford University, Stanford, California, USA (1986)

  18. Rogers, M.M., Mansour, N.N., Reynolds, W.C.: An algebraic model for the turbulent flux of a passive scalar. Journal of Fluid Mechanics 203, 77–101 (1989)

  19. Shabany, Y., Durbin, P.A.: Explicit algebraic scalar flux approximation. AIAA Journal 35, 985–989 (1997)

  20. So, R.M.C., Sommer, T.P.: A near-wall eddy conductivity model for fluids with different Prandtl numbers. Journal of Heat Transfer 116, 844–854 (1994)

  21. So, R.M.C., Sommer, T.P.: An explicit algebraic heat-flux model for the temperature field. International Journal of Heat and Mass Transfer 39, 455–465 (1996)

  22. So, R.M.C., Speziale, C.G.: A review of turbulent heat transfer modeling. Annual Review of Heat Transfer-X, C.L. Tien (Ed.), Begell House, Inc., New York, pp. 177–219 (1999)

  23. So, R.M.C., Zhao, C.Y., Gatski, T.B.: Predicting buoyant shear flows using anisotropic dissipation rate models. Journal of Flow, Turbulence and Combustion 63, 193–221 (1999)

  24. So, R.M.C., Vimala, P., Jin, L.H., Zhao, C.Y., Gatski, T.B.: An explicit algebraic stress model for homogeneous buoyant shear flows. Theoretical and Computational Fluid Dynamics 15, 283–302 (2002)

  25. So, R.M.C., Jin, L.H., Gatski, T.B.: An explicit algebraic Reynolds stress and heat flux model for incompressible turbulence: Part II Buoyant flow. Theoretical and Computational Fluid Dynamics, this issue – DOI 10.1007/s00162-004-0123-7 (2004)

  26. Sommer, T.P., So, R.M.C.: Wall-bounded buoyant turbulent flow and its modeling. International Journal of Heat and Mass Transfer 39, 3595–3606 (1996)

  27. Sommer, T.P., So, R.M.C., Zhang, J.: Modeling non-equilibrium and history effects of homogeneous turbulence in a stably stratified medium. Special Issue of the International Journal of Heat and Fluid Flow 18, 29–37 (1997)

  28. Spencer, A.J.M.: Theory of Invariants. In Continuum Physics, A.C. Eringen (Ed.), Academic Press, New York (1971)

  29. Speziale, C.G., Sarkar, S., Gatski, T.B.: Modelling the pressure-strain correlation of turbulence: an invariant dynamical systems approach. Journal of Fluid Mechanics 227, 245–272 (1991)

  30. Taulbee, D.B.: An improved algebraic Reynolds stress model and corresponding nonlinear stress model. Physics of Fluids A 4, 2555–2561 (1992)

  31. Ying, R., Canuto, V.M.: Turbulence modeling over two-dimensional hills using an algebraic Reynolds stress expression, Boundary-Layer Meteorology 77, 69–99 (1996)

  32. Wallin, S., Johansson, A.V.: An explicit algebraic Reynolds stress model for incompressible and compressible turbulent flows. Journal of Fluid Mechanics 403, 89–132 (2000)

  33. Wikstrom, P.M., Wallin, S., Johansson, A.V.: Derivation and investigation of a new explicit algebraic model for the passive scalar flux. Physics of Fluids 12, 688–702 (2000)

  34. Zhao, C.Y., So, R.M.C.: A geometry independent near-wall heat flux model for fluids with different Prandtl numbers. International Journal of Transport Phenomena 4, 1–16 (2002)

  35. Zhao, C.Y., So, R.M.C., Gatski, T.B.: Turbulence modeling effects on the prediction of equilibrium states of buoyant shear flows. Theoretical and Computational Fluid Dynamics 14, 399–422 (2001)

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, The Hong Kong Polytechnic University, Hung Hom, Kowloon, Hong Kong, P.R. China

    R.M.C. So

  2. Department of Engineering Mechanics, Tsinghua University, Beijing, 100084, P.R. China

    L.H. Jin

  3. Computational Modeling and Simulation Branch, NASA Langley Research Center, Hampton, VA, 23681-2199, USA

    T.B. Gatski

Authors
  1. R.M.C. So
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. L.H. Jin
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. T.B. Gatski
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to R.M.C. So.

Additional information

Communicated by

S. Thangam

Dedicated to the memory of the late Professor Charles G. Speziale of Boston University

Rights and permissions

Reprints and permissions

About this article

Cite this article

So, R., Jin, L. & Gatski, T. An explicit algebraic Reynolds stress and heat flux model for incompressible turbulence: Part I Non-isothermal flow. Theoret Comput Fluid Dynamics 17, 351–376 (2004). https://doi.org/10.1007/s00162-004-0122-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00162-004-0122-8

Keywords

Search

Navigation