Skip to main content
SpringerLink
Log in

Consistent tangent operator for an exact Kirchhoff rod model

  • Original Article
  • Published:
Continuum Mechanics and Thermodynamics Aims and scope Submit manuscript

Abstract

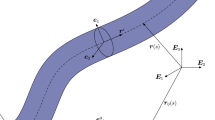
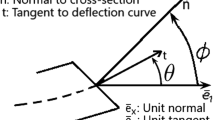
In the paper, it is considered an exact spatial Kirchhoff rod structural model. The configuration space for this model that has dimension 4 is obtained considering an ad hoc split of the rotation operator that implicitly enforces the constraints on the directors. The tangent stiffness operator, essential for the nonlinear numerical simulations, has been studied. It has been obtained as second covariant gradient of the internal energy functional for the considered structural model that preserves symmetry for any configuration, either equilibrated or not. The result has been reached evaluating the Levi-Civita connection for the tangent space of the configuration manifold. The results obtained extend to the case of Kirchoff -Love rods those presented by Simo (Comput Methods Appl Mech Eng 49:55–70, 1985) for Timoshenko rods. Given the different structure of the tangent spaces in this case, it has been necessary to introduce a specific metric that accounts for the rotation of the intrinsic triad due to the change of the position of the centroid axis of the rod.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Andreaus U., Dell’Isola F., Porfiri M.: Piezoelectric passive distributed controllers for beam flexural vibrations. JVC/ J. Vib. Control 10(5), 625–659 (2004)

    Article  MATH  Google Scholar 

  2. Antmann S.S.: Nonlinear Problem of Elasticity. Springer, New York (1995)

    Book  Google Scholar 

  3. Altenbach H., Eremeyev V.A.: On the effective stiffness of plates made of hyperelastic materials with initial stress. Int. J. Non-Linear Mech. 45(10), 976–981 (2010)

    Article  ADS  Google Scholar 

  4. Alessandroni S., Dell’Isola F., Porfiri M.: A revival of electric analogs for vibrating mechanical systems aimed to their efficient control by PZT actuators. Int. J. Solid Struct. 39(20), 5295–5324 (2002)

    Article  MATH  Google Scholar 

  5. Alibert J.-J., Seppecher P., Dell’Isola F.: Truss modular beams with deformation energy depending on higher displacement gradients. Math. Mech. Solids 8(1), 51–73 (2003)

    Article  MATH  MathSciNet  Google Scholar 

  6. Argyris J.: An excursion into large rotations. Comput. Methods Appl. Mech. Eng. 32, 85–155 (1982)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  7. Atluri S.N., Cazzani A.: Rotations in computational solid mechanics. Arch. Comput. Methods Eng. 2, 49–138 (1995)

    Article  MathSciNet  Google Scholar 

  8. Bergou M., Wardetzky M., Robinson S., Audoly B., Grinspun E.: Discrete elastic rod. ACM Trans. Graph. 27(3), 63–16312 (2008)

    Article  Google Scholar 

  9. Bersani A.M., Giorgio I., Tomassetti G.: Buckling of an elastic hemispherical shell with an obstacle. Contin. Mech. Thermodyn. 25(2), 443–467 (2013)

    Article  MathSciNet  ADS  Google Scholar 

  10. Betsch P., Steinmann P.: Frame-indifferent beam finite elements based upon the geometrically exact beam theory. Int. J. Numer. Meth. Eng. 54, 1775–1788 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  11. Birsan M., Altenbach H., Sadowski T., Eremeyev V.A., Pietras D.: Deformation analysis of functionally graded beams by the direct approach. Compos. Part B Eng. 43(3), 1315–1328 (2012)

    Article  Google Scholar 

  12. Crisfield M.A., Jelenic G.: Objectivity of strain measures in the geometrically exact three-dimensional beam theory and its finite-element implementation. Proc. R. Soc. Lond. 455, 1125–1147 (1999)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  13. Crisfield M.A.: Non-linear Finite Element Analysis of Solids and Structures, vol. 2, Advanced Topics. Wiley, New York (2000)

    Google Scholar 

  14. Cazzani A.: On the dynamics of a beam partially supported by an elastic foundation: an exact solution-set. Int. J. Struct. Stab. Dyn. 13, 1350045 (2013). doi:10.1142/S0219455413500454

    Article  MathSciNet  Google Scholar 

  15. Cuomo, M., Greco, L. : Isogeometric analysis of space rods: Considerations on stress locking. In ECCOMAS, pp. 1–19 (2012)

  16. Dell’Isola F., Vidoli S.: Continuum modeling of piezoelectromechanical truss beam: An application to vibration damping. Arch. Appl. Mech. 68(1), 1–19 (1998)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  17. Dell’Isola F., Porfiri M., Vidoli S.: Piezo-electromechanical (PEM) structures: Passive vibration control using distributed piezoelectric transducers. Comptes Rendus Mecanique 331(1), 69–76 (2003)

    Article  MATH  ADS  Google Scholar 

  18. Dell’Isola F., Seppecher P.: The relationship between edge contact forces, double forces and interstitial working allowed by principle of virtual power. Comptes Rendus De Lacademie des Sciences Serie II Fascicule B-Mecanique Physique Astronomie 321(8), 303–308 (1995)

    MATH  Google Scholar 

  19. Del Vescovo, D., Giorgio, I.: Dynamic problems for metamaterials: review of existing models and ideas for further research. Int. J. Eng. Sci, doi:10.1016/j.ijengsci.2014.02.002

  20. Dell’Isola F., Seppecher P., Madeo A.: How conctact interactions may depend on the shape of Cauchy cuts in Nth gradient continua: Approach “à à la D’Alambert”. Zeitschrift für Angewandte Mathematik und Physik 63(6), 1119–1141 (2012)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  21. Eremeyev V.A., Pietraszkiewicz W.: Local symmetry group in the general theory of elastic shell. J. Elast. 85(2), 125–152 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  22. Eremeyev V.A., Pietraszkiewicz W.: Phase transitions in thermoelastic and thermoviscoelastic shells. Arch. Mech. 61(1), 41–67 (2009)

    MATH  MathSciNet  Google Scholar 

  23. Eremeyev V.A., Pietraszkiewicz W.: The nonlinear theory of elastic shells with phase transitions. J. Elast. 74(1), 67–86 (2004)

    Article  MATH  MathSciNet  Google Scholar 

  24. Eremeyev V.A., Pietraszkiewicz W.: Thermomechanics of shells undergoing phase transition. J. Mech. Phys. 59(7), 1395–1412 (2011)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  25. Eugster, S.R., Hesch, C., Betsch, P., Glocker, Ch.: Director-based beam finite elements relying on the geometrically exact beam theory formulated in skew coordinates. Int. J. Numer. Meth. Eng. doi:10.1002/nme.4586

  26. Echter R., Oesterle B., Bischoff M.: A hierarchic family of isogeometric shell finite elements. Comput. Methods Appl. Mech. Eng. 254, 170–180 (2013)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  27. Ferretti, M., Madeo, A., Dell’Isola, F., Boisse, P.: Modeling the onset of shear boundary layers in fibrous composite reinforcements by second gradient theory. Zeitschrift für Angewandte Mathematik und Physik. doi:10.1007/s00033-013-0347-8

  28. Fox D.D., Simo J.C.: A drill rotation formulation for geometrically exact shells. Comput. Methods Appl. Mech. Eng. 98, 329–343 (1992)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  29. Giorgio I., Culla A., Del Vescovo D.: Multimode vibration control using several piezoelectric transducers shunted with a multiterminal network. Arch. Appl. Mech. 79, 859–879 (2009)

    Article  MATH  ADS  Google Scholar 

  30. Greco L., Cuomo M.: B-spline interpolation for Kirchhoff-Love space rod. Comput. Methods Appl. Mech. Eng. 256, 251–269 (2012)

    Article  MathSciNet  ADS  Google Scholar 

  31. Greco L., Cuomo M.: An implicit G 1 multi patch B-spline interpolation for Kirchhoff love space rod. Comput. Methods Appl. Mech. Eng. 269, 173–197 (2014)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  32. Ibrahimbegovic A.: On the geometrically exact formulation of structural mechanics and its applications to dynamics, control and optimization. Comptes-Rendus Mecanique 331, 383–394 (2003)

    Article  MATH  ADS  Google Scholar 

  33. Ibrahimbegovic A.: Stress resultant geometrically nonlinear shell theory with drilling rotations—Part I. A consistent formulation. Comput. Methods Appl. Mech. Eng. 118, 265–284 (1994)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  34. Ibrahimbegovic A., Frey F.: Stress resultant geometrically nonlinear shell theory with drilling rotations - Part II. Computational aspects. Comput. Methods Appl. Mech. Eng. 118, 285–308 (1994)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  35. Jelenic G., Saje M.: A kinematically exact space finite strain beam model—finite element formulation by generalized virtual work principle. J. Appl. Math. Phys. 120, 131–161 (1995)

    MATH  MathSciNet  Google Scholar 

  36. Jelenic G., Crisfield M.A.: Geometrically exact 3D beam theory: Implementation of a strain-invariant finite element for static and dynamics. Comput. Meth. Appl. Mech. Eng. 171, 141–171 (1999)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  37. Langer J., Singer D.A.: Lagrangian aspect of the Kirchhoff elastic rod. SIAM Rev. 38(4), 605–618 (1996)

    Article  MATH  MathSciNet  Google Scholar 

  38. Luongo A., Pignataro M.: Multiple interaction and localization phenomenon in postbuckling of compressed thin-walled members. AIAA J. 26(11), 1395–1402 (1988)

    Article  MATH  ADS  Google Scholar 

  39. Luongo A., Pignataro M.: On the perturbation analysis of interactive buckling in nearly symmetric structures. Int. J. Solids Struct. 29(6), 721–733 (1992)

    Article  MATH  Google Scholar 

  40. Luongo A.: Perturbation methods for nonlinear autonomous discrete-time dynamic systems. Nonlinear Dyn. 10(4), 317–331 (1996)

    Article  MathSciNet  Google Scholar 

  41. Luongo A., Di Egidio A., Paolone A.: Multiple scale bifurcation analysis for finite-dimensional autonomous systems. Recent Res. Dev. Sound Vib. 1, 161–201 (2002)

    Google Scholar 

  42. Luongo A.: Mode localization in dynamics and buckling of linear imperfect continuous structures. Nonlinear Dynamics 25(1-3), 133–156 (2001)

    Article  MATH  MathSciNet  Google Scholar 

  43. Luongo A., D’Annibale F.: Bifurcation analysis of damped visco-elastic planar beams under simultaneous gravitational and follower forces. Int. J. Modern Phys. B 26(25), 1246015-1–1246015-6 (2012)

    Article  ADS  Google Scholar 

  44. Luongo A., D’Annibale F.: Double zero bifurcation of non-linear viscoelastic beams under conservative and non-conservative loads. Int. J. Non-Linear Mech. 55, 128–139 (2013)

    Article  ADS  Google Scholar 

  45. Maurini C., Pouget J., Dell’Isola F.: On a model of layered piezoelectric beams including transverse stress effect. Int. J. Solid Struct. 41(16-17), 4473–4502 (2004)

    Article  MATH  Google Scholar 

  46. Paolone A., Vasta M., Luongo A.: Flexural-torsional bifurcations of a cantilever beam under potential and circulatory forces: Part I Nonlinear model and stability analysis. Int. J. Non-Linear Mech. 41(4), 586–594 (2006)

    Article  ADS  Google Scholar 

  47. Pietraszkiewicz W., Eremeyev V.A., Konopinska V.: Extended non-linear relations of elastic shells undergoing phase transitions. Z. Angew. Math. Mech. (ZAMM) 87(2), 150–159 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  48. Paolone A., Vasta M., Luongo A.: Flexural-torsional bifurcations of a cantilever beam under potential and circulatory forces: Part II Post-critical analysis. Int. J. Non-Linear Mech. 41(4), 595–604 (2006)

    Article  ADS  Google Scholar 

  49. Porfiri M., Dell’Isola F., Santini E.: Modeling and design of passive electric networks interconnecting piezoelectric transducers for distributed vibration control. Int. J. Appl. Electromagn. Mech. 21(2), 69–87 (2005)

    Google Scholar 

  50. Porfiri M., Dell’Isola F., Mascioli F.M.F.: Circuit analog of beam and its application to multimodal vibration damping, using piezoelectric transducers. Int. J. Circuit Theory Appl. 32(4), 167–198 (2004)

    Article  MATH  Google Scholar 

  51. Reissner E.: On finite deformations of space-curved beams. J. Appl. Math. Phys. 32, 734–744 (1981)

    Article  MATH  Google Scholar 

  52. Rodrigues O.: Des lois géométriques qui régissent les déplacements d’un systéme solide dans l’espace et de la variation des coornnées provenant de ces déplacements considéres indépendment des causes qui peuvent les produire. J. Math. Pures Appl. 5, 380–440 (1840)

    Google Scholar 

  53. Simo J.C.: A finite beam formulation, The three dimensional dynamic I. Comput. Methods Appl. Mech. Eng. 49, 55–70 (1985)

    Article  MATH  ADS  Google Scholar 

  54. Simo J.C., Vu-Quoc L.: A three-dimensional finite strain rod model, Part II: Computational aspects. Comput. Methods Appl. Mech. Eng. 58, 79–116 (1986)

    Article  MATH  ADS  Google Scholar 

  55. Smolenski WM: Statically and kinematically exact nonlinear theory of rods and its numerical verification. Comput. Methods Appl. Mech. Eng. 178, 89–113 (1999)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  56. Simo J.C., Vu-Quoc L.: On the dynamics in space of rods undergoing large motions. A geometrically exact approach. Comput. Methods Appl. Mech. Eng. 66, 125–161 (1988)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  57. Simo J.C., Fox D.D., Hughes T.J.R.: Formulations of finite elasticity with independent rotations. Comput. Methods Appl. Mech. Eng. 95, 277–288 (1992)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  58. Simo J.C.: The (symmetric) Hessian for geometrically nonlinear models in solids mechanics: Intrinsic definition and geometric interpretation. Comput. Methods Appl. Mech. Eng. 96, 189–200 (1992)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  59. Simo J.C., Marsden J.E., Krishnaprasad P.S.: The Hamiltonian structure of nonlinear elasticity: The material and convective representations of solid, rods, and plates. Arch. Ration. Mech. Anal. 104(2), 125–183 (1988)

    Article  MATH  MathSciNet  Google Scholar 

  60. Simo J.C., Fox D.D.: On a stress resultant geometrically exact shell model. Part I: Formulation and optimal parametrization. Comput. Methods Appl. Mech. Eng. 72, 267–304 (1989)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  61. Simo J.C., Fox D.D., Rifai M.S.: On a stress resultant geometrically exact shell model. Part II: the linear theory; Computational aspects. Comput. Methods Appl. Mech. Eng. 58, 79–116 (1989)

    Article  MathSciNet  Google Scholar 

  62. Vidoli S., Dell’Isola F.: Modal coupling in one-dimensional electromechanical structured continua. Acta Mech. 141(1), 37–50 (2000) Tuesday, April 29, 2014 at 4:34 pm

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. University of Catania, Catania, Italy

    L. Greco & M. Cuomo

Authors
  1. L. Greco
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. Cuomo
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. Cuomo.

Additional information

Communicated by Francesco dell'Isola and Giuseppe Piccardo.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Greco, L., Cuomo, M. Consistent tangent operator for an exact Kirchhoff rod model. Continuum Mech. Thermodyn. 27, 861–877 (2015). https://doi.org/10.1007/s00161-014-0361-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00161-014-0361-x

Keywords

Search

Navigation