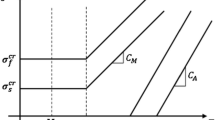
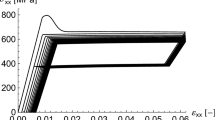
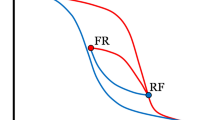
Abstract
A constitutive modeling approach for shape memory alloy (SMA) wire by taking into account the microstructural phase inhomogeneity and the associated solid–solid phase transformation kinetics is reported in this paper. The approach is applicable to general thermomechanical loading. Characterization of various scales in the non-local rate sensitive kinetics is the main focus of this paper. Design of SMA materials and actuators not only involve an optimal exploitation of the hysteresis loops during loading–unloading, but also accounts for fatigue and training cycle identifications. For a successful design of SMA integrated actuator systems, it is essential to include the microstructural inhomogeneity effects and the loading rate dependence of the martensitic evolution, since these factors play predominant role in fatigue. In the proposed formulation, the evolution of new phase is assumed according to Weibull distribution. Fourier transformation and finite difference methods are applied to arrive at the analytical form of two important scaling parameters. The ratio of these scaling parameters is of the order of 106 for stress-free temperature-induced transformation and 104 for stress-induced transformation. These scaling parameters are used in order to study the effect of microstructural variation on the thermo-mechanical force and interface driving force. It is observed that the interface driving force is significant during the evolution. Increase in the slopes of the transformation start and end regions in the stress–strain hysteresis loop is observed for mechanical loading with higher rates.
Similar content being viewed by others
References
Boyd J.G., Lagoudas D.C.: A thermodynamic constitutive model for shape memory materials. Part I. The monolithic shape memory alloy. Int. J. Plast. 12(6), 805–842 (1996)
Goo R.C., Lexcellent C.: Micromechanics-based modeling of two-way memory effect of a single crystalline shape memory alloy. Acta Mater. 45, 727–737 (1997)
Brocca M., Brinson L.C., Bazant Z.P.: Three-dimensional constitutive shape memory alloy based on microplane model. J. Mech. Phys. Solids 50, 1051–1077 (2002)
Siredey N., Patoor E., Bervellier M., Aberhardt E.: Constitutive equations for pollycrystalline thermoelastic shape memory alloys. Part I. Intragrannular interactions and behavior of the grain. Int. J. Solids Struct. 36, 4289–4315 (1999)
Ball J.M., Cartensen C.: Compatibility conditions for microstructures and the austenite–martensite transitions. Mater. Sci. Eng. A 273, 231–236 (1999)
Bhattacharya K.: Microstructure of Martensite. Oxford University Press, NY, USA (2003)
James R.D., Hane K.F.: Martensite Transformations and shape memory materials. Acta Mater. 48, 197–222 (2000)
Zhu J.J., Lew K.M.: Describing the morphology of 2H martensite using group theory. Part I. Theory. Mech. Adv. Mater. Struct. 11(3), 197–225 (2004)
Abeyaratne R., Chu C., James R.D.: Kinetics of materials with wiggly energies: the evolution of twinning microstructure in a Cu–Al–Ni shape memory alloys. Phil. Mag. 73, 457–496 (1996)
Artemev A., Wang Y., Khachaturyan A.G.: Three-dimensional phase field model and simulation of martensitic transformation in multilayer systems under applied stress. Acta Mater. 48, 2503–2518 (2000)
Ichitsubo T., Tanaka K., Koiwa M., Yamazaki Y.: Kinetics to cubic tetragonal transformation under external field by the time dependent Ginzburg–Landau approach. Phys. Rev. B 62, 5435 (2000)
Brinson L.C.: One dimensional constitutive behaviour of shape memory alloys: thermomechanical derivation with non-constant material functions. J. Intell. Mater. Syst. Struct. 4(2), 229–242 (1993)
Liang, C.: The constitutive modeling of shape memory alloy. Ph.D. thesis, Virginia Tech. (1990)
Niclaeys C., Zineb T.B., Chirani S.A., Patoor E.: Determination of interaction energy in the martensitic state. Int. J. Plast. 18, 1619–1647 (2002)
Falk F., Kanopka P.: Three-dimensional Landau theory describing the martensitic phase transformation of shape memory alloys. J. Phys. Condens. Mater. 2, 61–77 (1990)
Mahapatra D.R., Melnik R.V.N.: Finite element analysis of phase transformation dynamics in shape memory alloys with a consistent Landau–Ginzburg free energy model. Mech. Adv. Mater. Struct. 13, 443–445 (2006)
Van P.: The Ginzburg–Landau equation as a consequence of the second law. Continuum Mech. Thermodyn. 17, 165–169 (2005)
Rajagopal K.R., Srinivasa A.R.: On the thermomechanics of shape memory wires. ZAMP 50, 459–496 (1999)
Brenardini D.: Model of hysteresis in the framework of thermomechanics with internal variables. Phys. B 306, 132–136 (2001)
Brenardini D., Pence T.J.: Model for one-variant shape memory materials based on dissipation functions. Int. J. Nonlinear Mech. 37, 1299–1317 (2002)
Brenardini D., Pence T.J.: Uniaxial modelling of multivariant shape memory materials with internal sublooping using dissipation functions. Meccanica 40, 339–364 (2005)
Buravalla V.R., Khandelwal A.: Differential and integrated form consistency in 1-D phenomenological models for shape memory alloy constitutive behaviour. Int. J. Solids Struct. 44, 4369–4381 (2006)
Buravalla V.R., Khandelwal A.: A correction to the Brinson’s evolution kinetics for shape memory alloys. J. Intell. Mater. Syst. Struct. 19(1), 43–46 (2008)
Shaw J.A., Kyriakides S.: Thermomechanical aspects of NiTi. J. Mech. Phys. Solids 43(8), 1243–1281 (1995)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by T. Pence
Rights and permissions
About this article
Cite this article
Jha, V.K., Roy Mahapatra, D. Constitutive modeling of shape memory alloy wire with non-local rate kinetics. Continuum Mech. Thermodyn. 21, 1–15 (2009). https://doi.org/10.1007/s00161-009-0091-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00161-009-0091-7