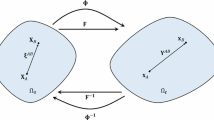
Abstract
The mathematical and physical analysis of magnetoelastic phenomena is a topic of ongoing research. Different formulae have been proposed to describe the magnetic forces in macroscopic systems. We discuss several of these formulae in the context of rigid magnetized bodies. In case the bodies are in contact, we consider formulae both in the framework of macroscopic electrodynamics and via a multiscale approach, i.e., in a discrete setting of magnetic dipole moments. We give mathematically rigorous proofs for domains of polygonal shape (as well as for more general geometries) in two and three space dimensions. In an accompanying second article, we investigate the formulae in a number of numerical experiments, where we focus on the dependence of the magnetic force on the distance between the bodies and on the case when the two bodies are in contact. The aim of the analysis as well as of the numerical simulation is to contribute to the ongoing debate about which formula describes the magnetic force between macroscopic bodies best and to stimulate corresponding real-life experiments.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Bobbio S. (2000). Electrodynamics of Materials: Forces, Stresses and Energies in Solids and Fluids. Academic, San Diego
Brown W.F. (1966). Magnetoelastic Interactions. Springer, Berlin
Döring W. (1968). Das elektromagnetische Feld, Vol. 2 of Einführung in die theoretische Physik. Walter de Gruyter&Co., Berlin
DeSimone A. and Podio-Guidugli P. (1996). On the continuum theory of deformable ferromagnetic solids. Arch. Ration. Mech. Anal. 136: 201–233
Eringen A.C. and Maugin G.A. (1990). Electrodynamics of Continua. Springer, New York
Egorov Yu.V. and Shubin M.A. (1998). Foundations of the Classical Theory of Partial Differential Equations. Springer, Berlin
Landau L.D., Lifschitz E.M.: Electrodynamics of continuous media, Vol. 8 of Course of theoretical physics, second edition. Pergamon, Oxford. Second Russian edition revised by Lifshitz and L.P. Pitaevskiĭ (1984)
Müller S. and Schlömerkemper A. (2002). Discrete-to-continuum limit of magnetic forces. C.R. Acad. Sci. Paris, Ser. I 335: 393–398
Popović N., Praetorius D., Schlömerkemper A.: Analysis and numerical simulation of magnetic forces between rigid polygonal bodies. Part II: Numerical simulation. Max Planck Institute for Mathematics in the Sciences, Leipzig, Preprint 64/2006, to appear in Contin. Mech. Thermodyn.
Popović N., Praetorius D. and Schlömerkemper A. (2005). Magnetic force formulae for magnets at small distances. PAMM Proc. Appl. Math. Mech. 5: 631–632
Schlömerkemper A.: About solutions of Poisson’s equation with transition condition in non-smooth domains. Max Planck Institute for Mathematics in the Sciences, Leipzig, Preprint 53/2006, to appear in Z. Anal. Anwend (2007)
Schlömerkemper A.: Lattice approximation of a surface integral and convergence of a singular lattice sum. Max Planck Institute for Mathematics in the Sciences, Leipzig, Preprint 86/2005, to appear in Asymptot. Anal (2007)
Schlömerkemper A.: Magnetic forces in discrete and continuous systems. PhD thesis, University of Leipzig, Leipzig (2002)
Schlömerkemper A. (2005). Mathematical derivation of the continuum limit of the magnetic force between two parts of a rigid crystalline material. Arch. Ration. Mech. Anal. 176: 227–269
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by A. DeSimone
Rights and permissions
About this article
Cite this article
Popović, N., Praetorius, D. & Schlömerkemper, A. Analysis and numerical simulation of magnetic forces between rigid polygonal bodies. Part I: Analysis. Continuum Mech. Thermodyn. 19, 67–80 (2007). https://doi.org/10.1007/s00161-007-0046-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00161-007-0046-9
Keywords
- Magnetostatics
- Magnetic force formulae
- Potential theory
- Partial differential equations
- Lattice-to-continuum limit