Abstract
Inductive sensors play a pivotal role in online oil debris detection and fault diagnosis. Inductive rotary coils are generally used in debris detection but lack high particle detection sensitivity. This paper proposes a shape optimization method to improve detection sensitivity and enhance sensor performance. The relative coil density is introduced as a shape parameter to quantify the geometry of the rotary coil and is decoupled from the coil size and wire arrangement. The signal formulas of arbitrarily shaped rotary coils are derived based on the relative coil density and reveal the effect of several coil parameters. This study provides general optimization methods for enhancing performance for application to microparticle inductance and resistance detection. To illustrate the benefit of the coil optimization method, the optimal coil shapes of various application cases are numerically designed and discussed. This optimization framework can be easily generalized to other application scenarios of rotary coils requiring optimization of magnetic field distribution.













Similar content being viewed by others
Abbreviations
- \({\varvec{r}}\), \(\widetilde{{\varvec{r}}}\) :
-
The position vectors of arbitrary point in coil space and characteristic detection point
- \({R}_{p}({\varvec{r}})\), \({L}_{p}({\varvec{r}})\) :
-
The resistance and inductance changes when the passing debris is at position \({\varvec{r}}\)
- \({\varvec{h}}\left({\varvec{r}}\right)\), \({\varvec{a}}({\varvec{r}})\) :
-
The magnetic strength and magnetic vector potential applied by a coil loaded with the direct unit current at \({\varvec{r}}\)
- \({\mu }_{0}\) :
-
Vacuum permeability \(\mu_{0} \, = \,4\pi \, \times \,10^{ - 7} \,H/m\)
- \({\eta }_{R}, {\eta }_{L}\) :
-
The coil basic inductance and resistance, \( \begin{array}{*{20}c} {\eta _{R} = R_{p} /R_{c} \eta _{L} = L_{p} /L_{c} } \\ \end{array} \)
- \({{\varvec{D}}}_{1}\) :
-
3D-local cylindrical coordinate space
- \({{\varvec{D}}}_{2}\) :
-
2D-local Cartesian coordinate space
- \(\widehat{{\varvec{\theta}}}\) :
-
The unit angular direct vector round z-axis
- \({{\varvec{\Omega}}}_{{\varvec{E}}}\) , \({{\varvec{\Omega}}}_{{\varvec{C}}}\) , \({\boldsymbol{ }\boldsymbol{ }\boldsymbol{\Omega }}_{{\varvec{F}}},\boldsymbol{ }\boldsymbol{ }{{\varvec{\Omega}}}_{{\varvec{O}}}\) :
-
The empty region, the region filled with coil wires, the region of flow path, and the design region
- \({\varvec{C}}\left({\varvec{r}}\right)\), \(C({\varvec{r}})\) :
-
The coil vector density at \({\varvec{r}}\) and the coil scalar density at \({\varvec{r}}\)
- \(C_{\max }\) :
-
The maximum coil density when coil wires are tightly wound
- \(c\left({\varvec{r}}\right)\) :
-
The relative coil density \(c({\varvec{r}})\)
- \({R}_{c}\left(c\right)\),\({ L}_{c}\left(c\right)\) :
-
The resistance and inductance of empty coil
- \(\omega \) :
-
Angular frequency of the excitation field
- \(\epsilon ,\beta \) :
-
Normalized \({R}_{2}\) and \(H\), namely, \(\frac{{R}_{2}}{P}\) and \(\frac{L}{P}\)
- \(\gamma ,\xi \) :
-
Normalized \(r\) and \(z\), namely, \(\frac{r}{P}\) and \(\frac{z}{P}\)
- \({v}_{p}\) :
-
Particle volume
- \({L}_{c}, {R}_{c}\) :
-
Empty-coil inductance and resistance
- \(\chi \) :
-
Magnetic susceptibility in an alternating magnetic field
- \(L\) :
-
Half of the winding length along the coil axis
- \({l}_{w}\) :
-
Total length of coil wire
- \({\sigma }_{m}\) :
-
Conductivity of metal
- \({\delta }_{m}\) :
-
Skin-depth of metal wire
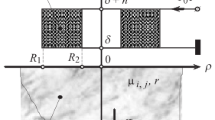
- \({R}_{1}{, R}_{2}\) :
-
Inner radius and outer radius of the coil
References
Du L, Zhe J (2011) A high throughput inductive pulse sensor for online oil debris monitoring. Tribol Int 44(2):175–179. https://doi.org/10.1016/J.TRIBOINT.2010.10.022
Encica L, Member S, Makarovic J, Lomonova EA, Vandenput AJ, Member S (2006) Space mapping optimization of a cylindrical voice coil actuator. IEEE Trans Ind Applicat. https://doi.org/10.1109/TIA.2006.882672
Fan B, Li B, Feng S, Mao J, Xie YB (2017) Modeling and experimental investigations on the relationship between wear debris concentration and wear rate in lubrication systems. Tribol Int 109:114–123. https://doi.org/10.1016/J.TRIBOINT.2016.12.015
Feng S, Yang L, Qiu G, Luo J, Li R, Mao J (2019) An inductive debris sensor based on a high-gradient magnetic field. IEEE Sens J 19(8):2879–2886. https://doi.org/10.1109/JSEN.2018.2890687
Grosz A, Paperno E (2012) Analytical optimization of low-frequency search coil magnetometers. IEEE Sens J 12(8):2719–2723. https://doi.org/10.1109/JSEN.2012.2202179
Hidaka Y, Sato T, Igarashi H (2014) Topology optimization method based on on-off method and level set approach. IEEE Trans Magn 50(2):617–620. https://doi.org/10.1109/TMAG.2013.2285379
Hiratsuka K, Muramoto K (2005) Role of wear particles in severe–mild wear transition. Wear 259(1–6):467–476. https://doi.org/10.1016/J.WEAR.2005.02.102
Jia F, Liu Z, Zaitsev M, Hennig J, Korvink JG (2014) Design multiple-layer gradient coils using least-squares finite element method. Struct Multidiscip Optim 49(3):523–535. https://doi.org/10.1007/S00158-013-0992-8/FIGURES/9
Jia R, Ma B, Zheng C, Ba X, Wang L, Du Q, Wang K (2019) Comprehensive improvement of the sensitivity and detectability of a large-aperture electromagnetic wear particle detector. Sensors 19(14):3162. https://doi.org/10.3390/S19143162
Li H, Wang K, Huang L, Li J, Yang X (2015) Coil structure optimization method for improving coupling coefficient of wireless power transfer. Conf Proc-IEEE Appl Power Electron Conf Expos-APEC. https://doi.org/10.1109/APEC.2015.7104704
Li Q, Chen W, Liu S, Tong L (2016) Structural topology optimization considering connectivity constraint. Struct Multidiscip Optim 54(4):971–984. https://doi.org/10.1007/S00158-016-1459-5/FIGURES/21
Li T, Wang S, Zio E, Shi J, Yang Z (2019) Aliasing signal separation for superimposition of inductive debris detection using CNN-based DUET. 2019 14th IEEE Conf Indus Electron Applicat (ICIEA) 8:211–215
Ma L, Zhang H, Qiao W, Han X, Zeng L, Shi H (2020) Oil metal debris detection sensor using ferrite core and flat channel for sensitivity improvement and high throughput. IEEE Sens J 20(13):7303–7309. https://doi.org/10.1109/JSEN.2019.2962698
Ostad-Ali-Askari K, Shayannejad M, Eslamian S, Zamani F, Shojaei N, Navabpour B, Majidifar Z, Sadri A, Ghasemi-Siani Z, Nourozi H, Vafaei O, Homayouni S-M-A (2017) Deficit irrigation : optimization models. Handbook Drought Water Scarcity. https://doi.org/10.1201/9781315226774-18
Palagani Y, Mohanarangam K, Shim JH, Choi JR (2019) Wireless power transfer analysis of circular and spherical coils under misalignment conditions for biomedical implants. Biosens Bioelectron 141:111283. https://doi.org/10.1016/J.BIOS.2019.04.051
Qian M, Ren Y, Zhao G, Feng Z (2021) Ultrasensitive inductive debris sensor with a two-stage autoasymmetrical compensation circuit. IEEE Trans Ind Electron 68(9):8885–8893. https://doi.org/10.1109/TIE.2020.3018066
Reed MA, Scott WR (2013) Coil optimization method for electromagnetic induction systems. IEEE Sens J. https://doi.org/10.1109/JSEN.2013.2270135
Reed MA, Scott WR (2014) Optimization of planar coils for electromagnetic induction systems. Int Geosci Remote Sens Symp (IGARSS). https://doi.org/10.1109/IGARSS.2014.6947009
Shi H, Zhang H, Wang W, Wang M, Zeng L (2019) Research on a novel method for detection of wear debris in hydraulic oil. Yi Qi Yi Biao Xue Bao/chin J Sci Instrum 40(9):44–51. https://doi.org/10.19650/j.cnki.cjsi.J1905360
Sun J, Wang L, Li J, Li F, Li J, Lu H (2021) Online oil debris monitoring of rotating machinery: a detailed review of more than three decades. Mech Syst Signal Process 149:107341. https://doi.org/10.1016/J.YMSSP.2020.107341
Svanberg K, Werme M (2006) Topology optimization by a neighbourhood search method based on efficient sensitivity calculations. Int J Numer Meth Eng 67(12):1670–1699. https://doi.org/10.1002/NME.1677
Tomasi D (2001) Stream function optimization for gradient coil design. Magn Reson Med. https://doi.org/10.1002/1522-2594
Wang M, Shi H, Zhang H, Huo D, Xie Y, Su J (2020) Improving the detection ability of inductive micro-sensor for non-ferromagnetic wear Debris. Micromachines 11(12):1108. https://doi.org/10.3390/MI11121108
Xue B, Zhang X, Xu Y, Li Y, Zhang H, Yu C (2021) Sparse signal recovery based on adaptive algorithms for debris detector. AIP Adv 11(6):065131. https://doi.org/10.1063/5.0050715
Zeng L, Wang W, Rogers F, Zhang H, Zhang X, Yang D (2020) A high sensitivity micro impedance sensor based on magnetic focusing for oil condition monitoring. IEEE Sens J 20(7):3813–3821. https://doi.org/10.1109/JSEN.2019.2958872
Zhang X, Zeng L, Zhang H, Huang S (2019) Magnetization model and detection mechanism of a microparticle in a harmonic magnetic field. IEEE/ASME Trans Mechatron 24(4):1882–1892. https://doi.org/10.1109/tmech.2019.2928704
Acknowledgements
The authors are grateful for the support from Shandong Provincial Key Research and Development Plan (No. 2021CXGC010702), National Natural Science Foundation of China (No. 51909047).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Replication of results
All the results in this research are obtained using Python codes. The source code and research data can be available from the corresponding author with reasonable requests.
Additional information
Responsible Editor: Yoojeong Noh
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Xue, B., Yu, C., Hua, G. et al. Arbitrary-cross-section rotary inductive coils for microparticle detection: analytical modeling, optimization and design. Struct Multidisc Optim 66, 154 (2023). https://doi.org/10.1007/s00158-023-03606-9
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00158-023-03606-9