Abstract
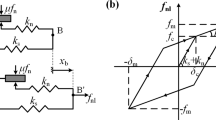
The hexagonal periodic structure of the honeycomb is a magic product of nature and shows great mechanical potential. In this work, a type of metamaterial vibration isolator with a honeycomb structure is proposed. The strain, deformation, and natural frequency of the vibration isolator are calculated by the two-dimensional plane finite element model and the simulation accuracies are validated by the experiments. As the design of the metamaterial vibration isolator involves time-consuming finite-element simulation, a multi-fidelity sequential optimization approach based on feasible region analysis (MF-FA) is proposed. In the proposed method, the refined and coarse mesh models are developed as the high- and low-fidelity models, and a two-phase multi-fidelity updating strategy is carried out. In the first phase, sample points are added to the constraint boundary to find the feasible solution quickly, in the second phase, the quality of the feasible optimization solution is gradually improved in the feasible region until it converges to the global optimal solution. Finally, the optimized metamaterial vibration isolator is manufactured and its superiority is validated. Results illustrate that the proposed approach can obtain a desirable optimum, whose natural frequency error between the experimental and the expected value is improved by 12.67% compared with the initial design.

















Similar content being viewed by others
References
Aridogan U, Basdogan I (2015) A review of active vibration and noise suppression of plate-like structures with piezoelectric transducers. J Intell Mater Syst Struct 26:1455–1476
Dong H, Song B, Wang P, Huang S (2015) Multi-fidelity information fusion based on prediction of kriging. Struct Multidiscip Optim 51:1267–1280
Fan HG, Yang LJ, Tian YC, Wang ZW (2020) Design of metastructures with quasi-zero dynamic stiffness for vibration isolation. Compos Struct 243:112244
Feldstein A, Lazzara D, Princen N, Willcox K (2020) Multifidelity data fusion: application to blended-wing-body multidisciplinary analysis under uncertainty. AIAA J 58:889–906
Han Z, Zimmerman R, Görtz S (2012) Alternative cokriging method for variable-fidelity surrogate modeling. AIAA J 50:1205–1210
Hassan AKS, Abdel-Malek HL, Mohamed AS, Elqenawy AE (2017) Space mapping surrogate-based microwave circuit design centering using a new statistical technique. Int J Numer Model El 30:e2108
Hu J, Zhou Q, McKeand A, Xie T, Choi SK (2021) A model validation framework based on parameter calibration under aleatory and epistemic uncertainty. Struct Multidiscip Optim 63(2):645–660
Ibrahim RA (2008) Recent advances in nonlinear passive vibration isolators. J Sound Vib 314:371–452
Koziel S, Bekasiewicz A (2018) Implicit space mapping for variable-fidelity EM-driven design of compact circuits. IEEE Microw Wirel Co 28:275–277
Le Gratiet L, Garnier J (2014) Recursive co-kriging model for design of computer experiments with multiple levels of fidelity. Int J Uncertain Quantif 4:365–386
Ma G, Sheng P (2016) Acoustic metamaterials: from local resonances to broad horizons. Sci Adv 2:e1501595
Mikhailov VP, Bazinenkov AM (2017) Active vibration isolation platform on base of magnetorheological elastomers. J Magn Magn Mater 431:266–268
Moscatelli M, Ardito R, Driemeier L, Comi C (2019) Band-gap structure in two- and three-dimensional cellular locally resonant materials. J Sound Vib 454:73–84
Park C, Haftka RT, Kim NH (2017) Remarks on multi-fidelity surrogates. Struct Multidiscip Optim 55:1029–1050
Pellegrini R, Iemma U, Leotardi C, Campana EF, Diez M (2016) Multi-fidelity adaptive global metamodel of expensive computer simulations, 2016 IEEE Congress on Evolutionary Computation (CEC). Publishing, pp 4444–4451
Plummer J (2015) Architectured materials snapping metamaterials. Nat Mater 14:962–962
Qian J, Yi J, Cheng Y, Liu J, Zhou Q (2020a) A sequential constraints updating approach for kriging surrogate model-assisted engineering optimization design problem. Eng Comput 36:993–1009
Qian J, Yi J, Zhang J, Cheng Y, Liu J (2020b) An entropy weight-based lower confidence bounding optimization approach for engineering product design. Appl Sci 10(10):3554
Rafsanjani A, Akbarzadeh A, Pasini D (2015) Snapping mechanical metamaterials under tension. Adv Mater 27:5931–5935
Rivin EI (2003) Passive vibration isolation. ASME Press, New York
Rokita T, Friedmann PP (2018) Multifidelity cokriging for high-dimensional output functions with application to hypersonic airloads computation. AIAA J 56:3060–3070
Shan S, Kang SH, Raney JR, Wang P, Fang L, Candido F, Lewis JA, Bertoldi K (2015) Multistable architected materials for trapping elastic strain energy. Adv Mater 27:4296–4301
Simonovic AM, Jovanovic MM, Lukic NS, Zoric ND, Stupar SN, Ilic SS (2016) Experimental studies on active vibration control of smart plate using a modified PID controller with optimal orientation of piezoelectric actuator. J Vib Control 22:2619–2631
Snowdon JC (1979) Vibration isolation: use and characterization. J Acoust Soc Am 66:1245–1274
Sun G, Li G, Stone M, Li Q (2010) A two-stage multi-fidelity optimization procedure for honeycomb-type cellular materials. Comput Mater Sci 49:500–511
Sun G, Li G, Li Q (2012) Variable fidelity design based surrogate and artificial bee colony algorithm for sheet metal forming process. Finite Elem Anal Des 59:76–90
Sun S, Song B, Wang P, Dong H, Chen X (2019) Shape optimization of underwater wings with a new multi-fidelity bi-level strategy. Struct Multidiscip Optim 61:319–341
Toman UT, Hassan A-KS, Owis FM, Mohamed AS (2019) Blade shape optimization of an aircraft propeller using space mapping surrogates. Adv Mech Eng 11:1687814019865071
Yan G, Zou HX, Wang S, Zhao LC, Gao QH, Tan T, Zhang WM (2020) Large stroke quasi-zero stiffness vibration isolator using three-link mechanism. J Sound Vib 478:115344
Zhonghua H, Chenzhou X, ZHANG L, ZHANG Y, ZHANG K, Wenping S (2020) Efficient aerodynamic shape optimization using variable-fidelity surrogate models and multilevel computational grids. Chin J Aeronaut 33:31–47
Zhou Q, Jiang P, Shao X, Hu J, Cao L, Wan L (2017) A variable fidelity information fusion method based on radial basis function. Adv Eng Inform 32:26–39
Zhou Q, Cao L, Zhou H, Huang X (2018) Prediction of angular distortion in the fiber laser keyhole welding process based on a variable-fidelity approximation modeling approach. J Intell Manuf 29:719–736
Zhou Q, Wu Y, Guo Z, Hu J, Jin P (2020) A generalized hierarchical co-Kriging model for multi-fidelity data fusion. Struct Multidiscip Optim 62:1885–1904
Funding
This work has been supported by the National Key Research and Development Program of China (Grant Number: 2018YFB1106705) and the National Natural Science Foundation of China (NSFC) under Grant No. 51805179 and No. 51721092.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Replication of results
The code could be downloaded from the website: https://pan.baidu.com/s/17qOCO_ny0HbjyXJlnGifww by using the code deeu.
Additional information
Responsible Editor: Palaniappan Ramu
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
ESM 1
(PDF 732 kb)
Rights and permissions
About this article
Cite this article
Qian, J., Cheng, Y., Zhang, A. et al. Optimization design of metamaterial vibration isolator with honeycomb structure based on multi-fidelity surrogate model. Struct Multidisc Optim 64, 423–439 (2021). https://doi.org/10.1007/s00158-021-02891-6
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00158-021-02891-6