Skip to main content
SpringerLink
Log in

Structural reliability analysis via dimension reduction, adaptive sampling, and Monte Carlo simulation

  • Research Paper
  • Published:
Structural and Multidisciplinary Optimization Aims and scope Submit manuscript

Abstract

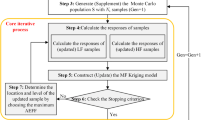
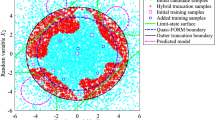
An improved reliability method, i.e., AL-AS-GPR-MCS, is developed taking advantage of active subspace (AS)-based dimension reduction technique, Gaussian process regression (GPR) surrogate model, active learning (AL)-based sampling strategy, and Monte Carlo simulation (MCS). In this method, the AL sampling strategy and the AS-based dimension reduction are incorporated into the GPR construction, allowing that the newly added sample in each iteration can be employed simultaneously to update the identified AS of original high-dimensional space and to refine the low-dimensional GPR model over the discovered AS. The failure probability is then estimated by the MCS using the constructed GPR model. In order to verify the versatility of the proposed method, four numerical examples are investigated, involving reliability analyses of both explicit performance functions and shear frame structures with implicit performance functions. It is revealed that satisfactory accuracy enhancement and computational cost savings are achieved by the AL-AS-GPR-MCS, since it is capable of discovering the latent AS of the original high-dimensional space which alleviates the curse of dimensionality, and refining the low-dimensional GPR construction within the discovered AS by the AL sampling strategy. Therefore, the proposed method is a powerful and promising tool for dealing with structural reliability problems with strong nonlinearities and high stochastic dimensions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  • Aas K, Czado C, Frigessi A, Bakken H (2009) Pair-copula constructions of multiple dependence. Insur Math Econ 44:182–198

    MathSciNet  MATH  Google Scholar 

  • Au SK, Beck JL (2001) Estimation of small failure probabilities in high dimensions by subset simulation. Probab Eng Mech 16(4):263–277

    Google Scholar 

  • Bect J, Ginsbourger D, Li L, Picheny V, Vazquez E (2012) Sequential design of computer experiments for the estimation of a probability of failure. Stat Comput 22(3):773–793

    MathSciNet  MATH  Google Scholar 

  • Bellman RE, Dreyfus SE (2015) Applied dynamic programming. Princeton university press

  • Bichon BJ, Eldred MS, Swiler LP, Mahadevan S, McFarland JM (2008) Efficient global reliability analysis for nonlinear implicit performance functions. AIAA J 46(10):2459–2468

    Google Scholar 

  • Coleman KD, Lewis A, Smith RC, Williams B, Morri M, Khuwaileh B (2019) Gradient-free construction of active subspaces for dimension reduction in complex models with applications to neutronics. SIAM/ASA J Uncertain Quantif 7(1):117–142

    MathSciNet  MATH  Google Scholar 

  • Constantine PG, Dow E, Wang Q (2014) Active subspace methods in theory and practice: applications to kriging surfaces. SIAM J Sci Comput 36(4):A1500–A1524

    MathSciNet  MATH  Google Scholar 

  • Constantine PG, Emory M, Larsson J, Iaccarino G (2015) Exploiting active subspaces to quantify uncertainty in the numerical simulation of the HyShot II scramjet. J Comput Phys 302:1–20

    MathSciNet  MATH  Google Scholar 

  • Deng J, Gu D, Li X, Yue ZQ (2005) Structural reliability analysis for implicit performance functions using artificial neural network. Struct Saf 27(1):25–48

    Google Scholar 

  • Der Kiureghian A, Dakessian T (1998) Multiple design points in first and second-order reliability. Struct Saf 20(1):37–49

    Google Scholar 

  • Ditlevsen O, Madsen HO (1996) Structural reliability methods. Wiley, New York

    Google Scholar 

  • Echard B, Gayton N, Lemaire M (2011) AK-MCS: an active learning reliability method combining Kriging and Monte Carlo simulation. Struct Saf 33(2):145–154

    Google Scholar 

  • Echard B, Gayton N, Lemaire M, Relun N (2013) A combined importance sampling and Kriging reliability method for small failure probabilities with time-demanding numerical models. Reliab Eng Syst Saf 111:232–240

    Google Scholar 

  • Engelund S, Rackwitz R (1993) A benchmark study on importance sampling techniques in structural reliability. Struct Saf 12(4):255–276

    Google Scholar 

  • Goodhue DL, Lewis W, Thompson R (2012) Does PLS have advantages for small sample size or non-normal data? MIS Quart Manage Inf Syst 36:981–1001

    Google Scholar 

  • Guimarães H, Matos JC, Henriques AA (2018) An innovative adaptive sparse response surface method for structural reliability analysis. Struct Saf 73:12–28

    Google Scholar 

  • Hino H, Wakayama K, Murata N (2013) Entropy-based sliced inverse regression. Comput Stat Data Anal 67:105–114

    MathSciNet  MATH  Google Scholar 

  • Huang X, Chen J, Zhu H (2016) Assessing small failure probabilities by AK-SS: an active learning method combining Kriging and Subset Simulation. Struct Saf 59:86–95

    Google Scholar 

  • Jiang Z, Li J (2017) High dimensional structural reliability with dimension reduction. Struct Saf 69:35–46

    Google Scholar 

  • Kaymaz I (2005) Application of kriging method to structural reliability problems. Struct Saf 27(2):133–151

    Google Scholar 

  • Kroetz HM, Tessari RK, Beck AT (2017) Performance of global metamodeling techniques in solution of structural reliability problems. Adv Eng Softw 114:394–404

    Google Scholar 

  • Lewis A, Smith R, Williams B (2016) Gradient free active subspace construction using Morris screening elementary effects. Comput Math Appl 72(6):1603–1615

    MathSciNet  MATH  Google Scholar 

  • Li J (2015) Probability density evolution method: background, significance and recent developments. Probab Eng Mech 44:111–117

    Google Scholar 

  • Li J, Chen J (2009) Stochastic dynamics of structures. John Wiley & Sons

  • Li B, Wang S (2007) On directional regression for dimension reduction. J Am Stat Assoc 102:997–1008

    MathSciNet  MATH  Google Scholar 

  • Li M, Wang Z (2019) Deep learning for high-dimensional reliability analysis. Mech Syst Signal Process. https://doi.org/10.1016/j.ymssp.2019.106399

  • Li J, Chen J, Sun W, Peng Y (2012) Advances of the probability density evolution method for nonlinear stochastic systems. Probab Eng Mech 28:132–142

    Google Scholar 

  • Li W, Lin G, Li B (2016) Inverse regression-based uncertainty quantification algorithms for high-dimensional models: theory and practice. J Comput Phys 321:259–278

    MathSciNet  MATH  Google Scholar 

  • Li DQ, Zheng D, Cao ZJ, Tang XS, Qi XH (2019) Two-stage dimension reduction method for meta-model based slope reliability analysis in spatially variable soils. Struct Saf 81:101872

    Google Scholar 

  • Liu H, Ong YS, Cai J (2018) A survey of adaptive sampling for global metamodeling in support of simulation-based complex engineering design. Struct Mutltidiscip Opt 57(1):393–416

    Google Scholar 

  • Ma F, Zhang H, Bockstedte A, Foliente GC, Paevere P (2004) Parameter analysis of the differential model of hysteresis. J Appl Mech Trans ASME 71(3):342–349

    MATH  Google Scholar 

  • Nelsen RB (2007) An introduction to copulas. Springer Science & Business Media

  • Pan Q, Dias D (2017) An efficient reliability method combining adaptive support vector machine and Monte Carlo simulation. Struct Saf 67:85–95

    Google Scholar 

  • Peng Y, Ghanem R, Li J (2013) Generalized optimal control policy for stochastic optimal control of structures. Structural Control and Health Monitoring, 20:67–89

  • Plessix RE (2006) A review of the adjoint-state method for computing the gradient of a functional with geophysical applications. Geophys J Int 167(2):495–503

    Google Scholar 

  • Rackwitz R (2001) Reliability analysis-a review and some perspective. Struct Saf 23(4):365–395

    Google Scholar 

  • Saltelli A, Ratto M, Andres T, Campolongo F, Cariboni J, Gatelli D et al (2008) Global sensitivity analysis: the primer. John Wiley & Sons

  • Seila AF (1982) Simulation and the Monte Carlo method. Taylor & Francis

  • Su G, Peng L, Hu L (2017) A Gaussian process-based dynamic surrogate model for complex engineering structural reliability analysis. Struct Saf 68:97–109

    Google Scholar 

  • Tripathy R, Bilionis I, Gonzalez M (2016) Gaussian processes with built-in dimensionality reduction: applications to high-dimensional uncertainty propagation. J Comput Phys 321:191–223

    MathSciNet  MATH  Google Scholar 

  • Wen Z, Yin W (2013) A feasible method for optimization with orthogonality constraints. Math Program 142(1–2):397–434

    MathSciNet  MATH  Google Scholar 

  • Williams CK, Rasmussen CE (2006) Gaussian processes for machine learning. MIT press Cambridge, MA

    MATH  Google Scholar 

  • Wold S, Sjöström M, Eriksson L (2001) PLS-regression: a basic tool of chemometrics. Chemometr Intell Lab Syst 58(2):109–130

    Google Scholar 

  • Xiu D, Em Karniadakis G (2003) The Wiener-Askey polynomial chaos for stochastic differential equations. SIAM J Sci Comput 24(2):619–644

    MathSciNet  MATH  Google Scholar 

  • Xu J, Wang D (2019) Structural reliability analysis based on polynomial chaos, Voronoi cells and dimension reduction technique. Reliab Eng Syst Saf 185:329–340

    Google Scholar 

  • Xu J, Zhu S (2019) An efficient approach for high-dimensional structural reliability analysis. Mech Syst Signal Process 122:152–170

    Google Scholar 

  • Zhang X, Pandey MD (2013) Structural reliability analysis based on the concepts of entropy, fractional moment and dimensional reduction method. Struct Saf 43:28–40

    Google Scholar 

  • Zhao YG, Ono T (2001) Moment methods for structural reliability. Struct Saf 23(1):47–75

    Google Scholar 

  • Zhou T, Li AQ (2019) Seismic fragility assessment of highway bridges using D-vine copulas. Bull Earthquake Engin 17:927–955

    Google Scholar 

  • Zhou T, Peng Y (2020) Adaptive Bayesian quadrature based statistical moments estimation for structural reliability analysis. Reliab Eng Syst Saf 198:106902

    Google Scholar 

  • Zhou T, Li AQ, Wu YF (2018) Copula-based seismic fragility assessment of base-isolated structures under near-fault forward-directivity ground motions. Bull Earthq Eng 16:5671–5696

    Google Scholar 

  • Zhou T, Peng Y, Li J (2019) An efficient reliability method combining adaptive global metamodel and probability density evolution method. Mech Syst Signal Process 131:592–616

    Google Scholar 

Download references

Funding

The supports of the National Key R&D Program of China (Grant No. 2017YFC0803300), the National Natural Science Foundation of China (Grant Nos. 51678450, 51878505, and 51725804), the Committee of Science and Technology of Shanghai China (Grant No. 18160712800), and the Ministry of Science and Technology of China (Grant No. SLDRCE19-B-26) are highly appreciated.

Author information

Authors and Affiliations

  1. State Key Laboratory of Disaster Reduction in Civil Engineering, Tongji University, Shanghai, 200092, People’s Republic of China

    Tong Zhou & Yongbo Peng

  2. College of Civil Engineering, Tongji University, Shanghai, 200092, People’s Republic of China

    Tong Zhou

  3. Shanghai Institute of Disaster Prevention and Relief, Tongji University, Shanghai, 200092, People’s Republic of China

    Yongbo Peng

Authors
  1. Tong Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yongbo Peng
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yongbo Peng.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Replication of results

The details of the proposed methodology and of the specific values of the parameters considered have been provided in the paper. Hence, we are confident that the results can be reproduced. Readers interested in the source code are encouraged to contact the authors by e-mail.

Additional information

Responsible Editor: Xiaoping Du

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhou, T., Peng, Y. Structural reliability analysis via dimension reduction, adaptive sampling, and Monte Carlo simulation. Struct Multidisc Optim 62, 2629–2651 (2020). https://doi.org/10.1007/s00158-020-02633-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00158-020-02633-0

Keywords

Search

Navigation