Skip to main content
SpringerLink
Log in

Multidisciplinary design of a guided flying vehicle using simplex nondominated sorting genetic algorithm II

  • RESEARCH PAPER
  • Published:
Structural and Multidisciplinary Optimization Aims and scope Submit manuscript

Abstract

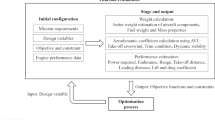
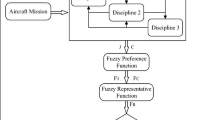
This paper presents design of a typical Guided Flying Vehicle (GFV) using the multidisciplinary design optimization (MDO). The main objectives of this multi-disciplinary design are maximizing the payload’s weight as well as minimizing the miss distance. The main disciplines considered for this design include aerodynamics, dynamic, guidance, control, structure, weight and balance. This design of GFV is applied to three and six Degree of Freedom (DOF) to show comparison of simulation results. The hybrid scheme of optimization algorithm is based on Nelder-Mead Simplex optimization algorithm and Nondominated Sorting Genetic Algorithm II (NSGA II), called Simplex-NSGA II. This scheme is implemented for finding an optimal solution through the MDO. The Simplex-NSGA II method is a heuristic optimization algorithm that applies to multi-objective functions and the results are then compared with the most famous algorithms, like Nondominated Sorting Genetic Algorithm II (NSGA II) and Multi-Objective Particle Swarm Optimization (MOPSO). Simulation results demonstrate the superior performance of the Simplex-NSGA II over NSGA II and MOPSO. Also, it is used in this study in order to achieve an optimal solution using MDO in both 3DOF and 6DOF simulations of GFV to reach desirable performance index.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

References

  • Anderson MB (1998) Design of a missile interceptor using genetic algorithms, Doctoral dissertation, Auburn University

  • Balesdent M, Bérend N, Dépincé P, Chriette A (2012) A survey of multidisciplinary design optimization methods in launch vehicle design. Struct Multidiscip Optim 45:619–642

    Article  MathSciNet  MATH  Google Scholar 

  • Bayley DJ, Hartfield RJ (2007) Design optimization of space launch vehicles for minimum cost using a genetic algorithm. In AIAA 43rd AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, AIAA, paper, vol. 5852. 2007

  • Bayley DJ, Hartfield RJ, Burkhalter JE, Jenkins RM (2008) Design optimization of a space launch vehicle using a genetic algorithm. J Spacecr Rocket 45:733–740

    Article  Google Scholar 

  • Blake WB (1998) Missile Datcom: User's Manual-1997 FORTRAN 90 Revision (No. AFRL-VA-WP-TR-1998–3009). AIR FORCE RESEARCH LAB WRIGHT-PATTERSON AFB OH AIR VEHICLES DIRECTORATE

  • Coello CAC, Pulido GT, Lechuga MS (2004) Handling multiple objectives with particle swarm optimization. IEEE Transactions on evolutionary computation, 8(3), pp.256–279.

  • Deb K, Pratap A, Agarwal S, Meyarivan T (2002) A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans Evol Comput 6:182–197. doi:10.1109/4235.996017

    Article  Google Scholar 

  • Ebrahimi M, Farmani MR, Roshanian J (2011) Multidisciplinary design of a small satellite launch vehicle using particle swarm optimization. Struct Multidiscip Optim 44:773–784

    Article  Google Scholar 

  • Eugene LF (2001) Tactical missile design. AIAA Education Series.

  • Fourie PC, Groenwold AA (2002) The particle swarm optimization algorithm in size and shape optimization. Struct Multidiscip Optim 23:259–267

    Article  Google Scholar 

  • Hemsch MJ, Nielsen JN (1986) Tactical missile aerodynamics, NASA Ames Research Senter, CA, United States

  • Li X, Wang D (2009) Design of Guidance and Control law for aerial guided bomb [J]. Aero Weapon 3:5

    Google Scholar 

  • Liu Z, Chen G (2010) Uncontrolled flying simulation of guided bomb [J]. J Xi’an Technol Univ 3:16

    Google Scholar 

  • Nebro AJ, Durillo JJ, Coello CAC (2013) Analysis of leader selection strategies in a multi-objective particle swarm optimizer. In Evolutionary Computation (CEC), 2013 IEEE Congress on (pp. 3153–3160). IEEE

  • Pourtakdoust SH, Zandavi SM (2016) A Hybrid Simplex Non-dominated Sorting Genetic Algorithm for Multi-Objective Optimization. Int J Swarm Intel Evol Comput 5:138. doi:10.4172/2090-4908.1000138

  • Pradhan PM, Panda G (2012) Solving multiobjective problems using cat swarm optimization. Expert Syst Appl 39:2956–2964. doi:10.1016/j.eswa.2011.08.157

    Article  Google Scholar 

  • Rafique AF, Zeeshan Q, Linshu H (2008) Conceptual design of small satellite launch vehicle using hybrid optimization. In: Sivasundaram S (ed) Seventh international conference on mathematical problems in engineering, aerospace and sciences. Cambridge Scientific Publishers Ltd, Cambridge, pp 681–697

    Google Scholar 

  • Rafique AF, He LS, Zeeshan Q (2009) Multidisciplinary design of air-launched satellite launch vehicle using particle swarm optimization. In: Anderssen RS, Braddock RD, Newham LTH (eds) 18th world IMACS congress and MODSIM09 international congress on modelling and simulation. Modelling and Simulation Society of Australia and New Zealand and International Association for Mathematics and Co. Citeseer, Canberra, pp 418–424

    Google Scholar 

  • Rao SS (1996) Engineering optimization: theory and practice. New Delhi: New Age Internation (P) Limited, Puiblishers

  • Roskam J (1995) Airplane flight dynamics and automatic flight controls. DARcorporation

  • Schott JR (1995) Fault tolerant design using single and multicriteria genetic algorithm optimization. DTIC Document

  • Schutte JF, Groenwold AA (2003) Sizing design of truss structures using particle swarms. Struct Multidiscip Optim 25:261–269

    Article  Google Scholar 

  • Sierra MR, Coello Coello CA (2005) March. Improving PSO-based multi-objective optimization using crowding, mutation and e-dominance. In Evolutionary multi-criterion optimization (Vol. 3410, pp. 505–519). Berlin, Germany: Springer

  • Siouris GM (2004) Missile guidance and control systems. Springer Science & Business Media

  • Sobieski I (1993) Multidisciplinary design optimization: attempt at definition. In: Industry university workshop on multidisciplinary aircraft design. pp 23–48

  • Venter G, Sobieszczanski-Sobieski J (2003) Particle swarm optimization. AIAA J 41:1583–1589

    Article  Google Scholar 

  • Wang J, Lv S, Zhang M, Guo R (2012) The design and simulation of the control system for a guided rocket [J]. J Proj Rocket Missiles Guid 1:18

    Google Scholar 

  • Xiaozhong X, Chuanjie S (2004) Optimization design for the ballistics of simply guided bombs. Acta Armamentarii 25:376–378

    Google Scholar 

  • Zhang Q, Zhou A, Zhao S Suganthan PN, Liu W, & Tiwari S, (2008). Multiobjective optimization test instances for the CEC 2009 special session and competition. University of Essex, Colchester, UK and Nanyang technological University, Singapore, special session on performance assessment of multi-objective optimization algorithms, technical report, 264

  • Zitzler E, Thiele L (1999) Multiobjective evolutionary algorithms: a comparative case study and the strength Pareto approach. Evol Comput IEEE Trans 3:257–271. doi:10.1109/4235.797969

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Information Technologies, University of Sydney, Sydney, Australia

    Seid Miad Zandavi

  2. Department of Aerospace Engineering, Sharif University of Technology, Tehran, Iran

    Seid H. Pourtakdoust

Authors
  1. Seid Miad Zandavi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Seid H. Pourtakdoust
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Seid Miad Zandavi.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zandavi, S.M., Pourtakdoust, S.H. Multidisciplinary design of a guided flying vehicle using simplex nondominated sorting genetic algorithm II. Struct Multidisc Optim 57, 705–720 (2018). https://doi.org/10.1007/s00158-017-1776-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00158-017-1776-3

Keywords

Search

Navigation