Skip to main content
SpringerLink
Log in

An immersed boundary approach for shape and topology optimization of stationary fluid-structure interaction problems

  • RESEARCH PAPER
  • Published:
Structural and Multidisciplinary Optimization Aims and scope Submit manuscript

Abstract

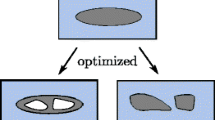
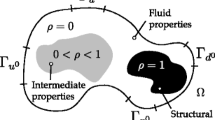
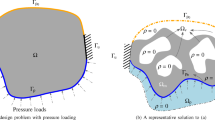
This paper presents an approach to shape and topology optimization of fluid-structure interaction (FSI) problems at steady state. The overall approach builds on an immersed boundary method that couples a Lagrangian formulation of the structure to an Eulerian fluid model, discretized on a deforming mesh. The geometry of the fluid-structure boundary is manipulated by varying the nodal parameters of a discretized level set field. This approach allows for topological changes of the fluid-structure interface, but free-floating volumes of solid material can emerge in the course of the optimization process. The free-floating volumes are tracked and modeled as fluid in the FSI analysis. To sense the isolated solid volumes, an indicator field described by linear, isotropic diffusion is computed prior to analyzing the FSI response of a design. The fluid is modeled with the incompressible Navier-Stokes equations, and the structure is assumed linear elastic. The FSI model is discretized by an extended finite element method, and the fluid-structure coupling conditions are enforced weakly. The resulting nonlinear system of equations is solved monolithically with Newton’s method. The design sensitivities are computed by the adjoint method and the optimization problem is solved by a gradient-based algorithm. The characteristics of this optimization framework are studied with two-dimensional problems at steady state. Numerical results indicate that the proposed treatment of free-floating volumes introduces a discontinuity in the design evolution, yet the method is still successful in converging to meaningful designs.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22

Similar content being viewed by others

References

  • Allaire G, Jouve F, Toader A (2002) A level-set method for shape optimization. C.R Math 334 (12):1125–1130

    Article  MathSciNet  MATH  Google Scholar 

  • Allaire G, Jouve F, Toader AM (2004) Structural optimization using sensitivity analysis and a level-set method. J Comput Phys 194(1):363–393

    Article  MathSciNet  MATH  Google Scholar 

  • Allaire G, Dapogny C, Frey P (2014) Shape optimization with a level set based mesh evolution method. Comput Methods Appl Mech Eng 282:22–53

    Article  MathSciNet  Google Scholar 

  • Allen M, Maute K (2004) Reliability based optimization of aeroelastic structures. Struct Multidiscip Optim 24:228–242

    Article  Google Scholar 

  • Allen M, Maute K (2005) Reliability-based shape optimization of structures undergoing fluid structure interaction phenomena. Comput Methods Appl Mech Eng 194:3472–3495

    Article  MATH  Google Scholar 

  • Amestoy P, Duff I, L’Excellent JY (2000) Multifrontal parallel distributed symmetric and unsymmetric solvers. Comput Methods Appl Mech Eng 184(24):501–520

    Article  MATH  Google Scholar 

  • Annavarapu C, Hautefeuille M, Dolbow JE (2012) A robust nitsches formulation for interface problems. Comput Methods Appl Mech Eng 225228(0):44–54

    Article  MathSciNet  MATH  Google Scholar 

  • Arora D, Behr M, Pasquali M (2004) A tensor-based measure for estimating blood damage. Artif Organs 28:1002–1115

    Article  Google Scholar 

  • Bazilevs Y, Takizawa K, Tezduyar TE (2013) Computational Fluid-Structure Interaction: Methods and applications Wiley; 1 edition (February 11, 2013)

  • Bendsøe M (1989) Optimal shape design as a material distribution problem. Struct Multidiscip Optim 1 (4):193–202

    Article  Google Scholar 

  • Brampton C, Kim HA, Cuningham J (2012) Level set topology optimisation of aircraft wing considering aerostructural interaction. In: 12th AIAA Aviation Technology, Integration, and Opterations (ATIO) Conference and 14th AIAA/ISSM Multidisciplinary Analysis and Optimization Conference, Indianapolis, IN, September 17 - 19

  • Burger M, Osher SJ (2005) A survey in mathematics for industry a survey on level set methods for inverse problems and optimal design. Euro Jnl of Appl Math 16:263–301

    Article  MathSciNet  MATH  Google Scholar 

  • Butler R, Lillico M, Banerjee J, Guo S (1995) Optimum design of high aspect ratio wings subject to aeroelastic constraints. In: Structures, Structural Dynamics, and Materials and Co-located Conferences, American Institute of Aeronautics and Astronautics

  • Christiansen AN (2014) Combined shape and topology optimization. PhD thesis, Technical University of Denmark

  • Coffin P, Maute K (2015) A level-set method for steady-state and transient natural convection problems. Structural and Multidisciplinary Optimization 1–21

  • Dapogny C (2014) Shape optimization, level set methods on unstructured meshes and mesh evolution. PhD thesis, Thèse de lUniversité Paris VII

  • van Dijk N, Maute K, Langelaar M, Keulen F (2013) Level-set methods for structural topology optimization: A review. Structural and Multidisciplinary Optimization 1–36

  • Dillinger J, Abdalla M, Klimmek T, Gurdal Z (2013) Static aeroelastic stiffness optimization and investigation of forward swept composite wings. In: 10th World Congress on Structural and Multidisplinary Optimization. May 19 - 24, Orlando, Florida

  • Dunning P, Stanford B, Kim H (2014) Coupled aerostructural topology optimization using a level set method for 3d aircraft wings. Structural and Multidisciplinary Optimization 1–20

  • Dunning P, Stanford B, Kim HA (2015) Coupled aerostructural topology optimization using level set method for 3d aircraft wings. Struct Multidiscip Optim 51:1113–1132

  • Gasbarri P, Chiwiacowsky LD, de Campos Velho H (2009) A hybrid multilevel approach for aeroelastic optimization of composite wing-box. Struct Multidiscip Optim 39(6):607–624

    Article  MathSciNet  MATH  Google Scholar 

  • Gern FH, Gundlach JF, Ko A, Naghshineh-Pour A, Sulaeman E, Tetrault PA, Grossman B, Kapania RK, Mason WH, Schetz JA, Haftka R (1999). In: Multidisciplinary design optimization of a transonic commercial transport with a strut-braced wing 1999 World Aviation Congress, San Franciso, CA, October 19 - 21

  • Ghazlane I, Carrier G, Dumont A, Marcelet M, Désidéri JA (2011) Aerostructural optimization with the adjoint method. In: EUROGEN 2011, Capua, Italy, September 14 - 15

  • Gomes AA, Suleman A (2008) Topology optimization of a reinforced wing box for enhanced roll maneuvers. AIAA J 46:548–556

    Article  Google Scholar 

  • Griffith BE (2012) Immersed boundary model of aortic heart valve dynamics with physiological driving and loading conditions. Int J Numer Methods Biomed Eng 28(3):317–345

    Article  MathSciNet  MATH  Google Scholar 

  • Gumbert CR, Hou GJW, Newman PA (2001) Simultaneous aerodynamic analysis and design optimization (saado) for a 3-d flexible wing. In: Proceedngs of the 39th Aerospace Science Meeting and Exhibit, January 8-11, 2001, Reno, NV, AIAA 2001- 1107

  • Guo S (2007) Aeroelastic optimization of an aerobatic aircraft wing structure. Aerosp Sci Technol 11(5):396–404

    Article  MATH  Google Scholar 

  • Guo S, Cheng W, Cui D (2005) Optimization of composite wing structures for maximum flutter speed. In: 46th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics & Materials Conference, Austin, TX, April 21 - 25

  • Hansbo P, Hermansson J, Svedberg T (2004) Nitsches method combined with space-time finite elements for ale fluid-structure interaction problems. Comput Methods Appl Mech Engrg 193:4195–4206

    Article  MathSciNet  MATH  Google Scholar 

  • Hart JD (2002) Fluid-structure interaction in the aortic heart valve a three-dimensional computational analysis. PhD thesis, Technische Universiteit Eindhoven

  • Hsu MC, Kamensky D, Bazilevs Y, Sacks M, Hughes T (2014) Fluidstructure interaction analysis of bioprosthetic heart valves: significance of arterial wall deformation. Comput Mech 54(4):1055–1071

    Article  MathSciNet  MATH  Google Scholar 

  • James K, Martins J (2010) Topology optimization using a level set method with an arbitrary structured mesh. In: 51st AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Orlando, FL, April 12 - 16

  • Jenkins N, Maute K (2015) Level set topology optimization of stationary fluid-structure interaction problems. Struct Multidiscip Optim 52:179–195

    Article  MathSciNet  Google Scholar 

  • Kamensky D, Hsu MC, Schillinger D, Evans JA, Aggarwal A, Bazilevs Y, Sacks MS, Hughes TJ (2015) An immersogeometric variational framework for fluidstructure interaction: Application to bioprosthetic heart valves. Comput Methods Appl Mech Eng 284(0):1005–1053

    Article  MathSciNet  Google Scholar 

  • Kreissl S, Maute K (2011) Topology optimization for unsteady flow. Int J Numer Methods Eng 87:1229–1253

    MathSciNet  MATH  Google Scholar 

  • Krog L, Tucker A, Rollema G (2002) Application of topology, sizing and shape optimization methods to optimal design of aircraft components. In: 3 rd Altair UK HyperWorks Users Conference

  • Krog L, Tucker A, Kemp M, Boyd R (2004) Topology optimization of aircraft wing box ribs. In: 10th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, August 30 - September 1, Albany, New York

  • Liu S, Li Q, Chen W, Tong L, Cheng G (2015) An identification method for enclosed voids restriction in manufacturability design for additive manufacturing structures. Front Mech Eng 10(2):126–137

    Article  Google Scholar 

  • Lund E, Moller H, Jakobsen LA (2001) Shape design optimization of steady fluid-structure interaction problems with large displacements. In: 42cd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference and Exhibit. April 16-19

  • Luo Z, Tong L, Wang MY, Wang S (2007) Shape and topology optimization of compliant mechanisms using a parameterization level set method. J Comput Phys 227(1):680–705

    Article  MathSciNet  MATH  Google Scholar 

  • Makhija D, Maute K (2014) Numerical instabilities in level set topology optimization with the extended finite element method. Struct Multidiscip Optim 49(2):185–197

    Article  MathSciNet  Google Scholar 

  • Martins J, Alonso J, Reuther J (2005) A coupled-adjoint sensitivity analysis method for high-fidelity aero-structural design. Optim Eng 6(1):33–62

    Article  MATH  Google Scholar 

  • Martins J RRA, Alonso JJ, Reuther JJ (2004) High-fidelity aerostructural design optimization of a supersonic business jet. J Aircr 41(3)

  • Maute K, Reich G (2006) Integrated multidisciplinary topology optimization approach to adaptive wing design. AIAA J Aircr 43(1):253–263

    Article  Google Scholar 

  • Maute K, Nikbay M, Farhat C (2001) Coupled analytical sensitivity analysis and optimization of three-dimensional nonlinear aeroelastic systems. AIAA J 39(11):2051–2061

    Article  MATH  Google Scholar 

  • Maute K, Nikbay M, Farhat C (2003) Sensitivity analysis and design optimization of three-dimensional nonlinear aeroelastic systems by the adjoint method. Int J Numer Methods Eng 56(6):911–933

    Article  MATH  Google Scholar 

  • Mayer U, Popp A, Gerstenberger A, Wall W (2010) 3d fluidstructure-contact interaction based on a combined xfem fsi and dual mortar contact approach. Comput Mech 46(1):53–67

    Article  MathSciNet  MATH  Google Scholar 

  • Morbiducci U, Ponzini R, Nobili M, Massai D, Montevecchi FM, Bluestein D, Redaelli A (2015) Blood damage safety of prosthetic heart valves. shear-induced platelet activation and local flow dynamics: A fluidstructure interaction approach. J Biomech 42:1952–1960

    Article  Google Scholar 

  • Munk D, Vio G, Steven G (2015) Aerothermoelastic structural topology optimisation for a hypersonic transport aircraft wing. In: 11th World Congress on Structural and Mutlidisciplinary Optimization. June 7 - 12, Sydney, Australia

  • Osher SJ, Sethian JA (1988) Fronts propagating with curvature dependent speed: algorithms based on Hamilton-Jacobi formulations. J Comput Phys 79:12—49

    Article  MathSciNet  MATH  Google Scholar 

  • Picelli R, Vicente WM, Pavanello R, van Keulan F (2015) Topology optimization considering design-dependent stokes flow loads. In: 11th World Congress on Structural and Multidisciplinary Optimization. Sydney Australia, June 7 - 12

  • Pingen G, Waidmann M, Evgrafov A, Maute K (2010) A parametric level-set approach for topology optimization of flow domains. Struct Multidiscip Optim 41(1):117–131

    Article  MathSciNet  MATH  Google Scholar 

  • Sala M, Stanley KS, Heroux MA (2008) On the design of interfaces to sparse direct solvers. ACM Trans Math Softw 34(2):9:1–9:22

    MathSciNet  MATH  Google Scholar 

  • Schleupen A, Maute K, Ramm E (2000) Adaptive fe-procedures in shape optimization. Struct Multidiscip Optim 19:282–302

    Article  Google Scholar 

  • Sigmund O, Maute K (2013) Topology optimization approaches: A comparative review. Struct Multidiscip Optim 48(6):1031–1055

    Article  MathSciNet  Google Scholar 

  • Sobieszczanski-Sobieski J, Haftka R (1997) Multidisciplinary aerospace design optimization: survey of recent developments. Struct Optim 14(1):1–23

    Article  Google Scholar 

  • Stanford B (2008) Aeroelastic analysis and optimization of membrane micro air vehicle wings. PhD thesis, University of Florida

  • Stanford B, Beran P (2013) Aerothermoelastic topology optimization with flutter and buckling metrics. Struct Multidiscip Optim 48(1):149–171

    Article  MathSciNet  MATH  Google Scholar 

  • Stanford B, Ifju P (2009) Aeroelastic topology optimization of membrane structures for micro air vehicles. Struct Multidiscip Optim 38(3):301–316

    Article  Google Scholar 

  • Svanberg K (2002) A class of globally convergent optimization methods based on conservative convex separable approximations. SIAM J on Optim 12(2):555–573

    Article  MathSciNet  MATH  Google Scholar 

  • Terada K, Asai M, Yamagishi M (2003) Finite cover method for linear and non-linear analyses of heterogeneous solids. Int J Numer Methods Eng 58(9):1321–1346

    Article  MATH  Google Scholar 

  • Tezduyar TE, Mittal S, Ray SE, Shih R (1992) Incompressible flow computations with stabilized bilinear and linear equal-order-interpolation velocity-pressure elements. Comput Methods Appl Mech Eng 95:221–242

    Article  MATH  Google Scholar 

  • Tran AB, Yvonnet J, He QC, Toulemonde C, Sanahuja J (2011) A multiple level set approach to prevent numerical artifacts in complex microstructures with nearby inclusions within xfem. Int J Numer Methods Eng 85(11):1436–1459

    Article  MATH  Google Scholar 

  • Vasava P, Jalali P, Dabagh M, Kolari PJ (2012) Finite element modelling of pulsatile blood flow in idealized model of human aortic arch: Study of hypotension and hypertension. Comput Math Methods Med 861837:1748–6718

    MathSciNet  MATH  Google Scholar 

  • Villanueva CH, Maute K (2014) Density and level set-xfem schemes for topology optimization of 3-d structures. Comput Mech 54(1):133–150

    Article  MathSciNet  MATH  Google Scholar 

  • Wang MY, Wang X, Guo D (2003) A level set method for structural topology optimization. Comput Methods Appl Mech Eng 192(1–2):227–246

    Article  MathSciNet  MATH  Google Scholar 

  • Wang S, Wang M (2006) Radial basis functions and level set method for structural topology optimization. Int J Numer Methods Eng 65(12):2060–2090

    Article  MathSciNet  MATH  Google Scholar 

  • Yoon GH (2010) Topology optimization for stationary fluid–structure interaction problems using a new monolithic formulation. Int J Numer Methods Eng 82(5):591–616

    Article  MATH  Google Scholar 

  • Yoon GH (2014) Stress-based topology optimization method for steady-state fluidstructure interaction problems. Comput Methods Appl Mech Eng 278(0):499–523

    Article  Google Scholar 

  • Zhou M, Rozvany GIN (1991) The COC algorithm, part II: Topological, geometrical and generalized shape optimization. Comput Methods Appl Mech Eng 89(1–3):309–336

    Article  Google Scholar 

Download references

Acknowledgments

The authors acknowledge the support of the National Science Foundation under grant CMMI 1235532. The opinions and conclusions presented in this paper are those of the authors and do not necessarily reflect the views of the sponsoring organization.

Author information

Authors and Affiliations

  1. Department of Aerospace Engineering Sciences, University of Colorado at Boulder, 429 UCB, Boulder, CO, 80309, USA

    Nicholas Jenkins & Kurt Maute

Authors
  1. Nicholas Jenkins
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Kurt Maute
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Kurt Maute.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jenkins, N., Maute, K. An immersed boundary approach for shape and topology optimization of stationary fluid-structure interaction problems. Struct Multidisc Optim 54, 1191–1208 (2016). https://doi.org/10.1007/s00158-016-1467-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00158-016-1467-5

Keywords

Search

Navigation