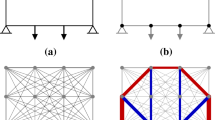
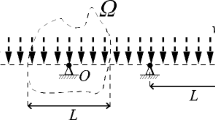
Abstract
Beghini et al. (Struct Multidisc Optim 50:49–64, 2014) have published a very interesting paper arriving to practically the same nearly optimal solutions for the so named “bridge problem” that the writers published a year before, but using an alternative and remarkable approach to the problem. In spite of this general agreement, the writers think that some details of the paper can be improved and there are results that can be given a clear and meaningful interpretation, thanks to an old and practically unknown theorem on optimal slenderness.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Beghini A, Beghini LL, Baker WF (2014) On the layout of a least weight single span structure with uniform load. Struct Multidisc Optim 50:49–64. doi:10.1007/s00158-013-1030-6
Cervera Bravo J, Vázquez Espí C, Vázquez Espí M (2014) Two near-optimal layouts for truss-like bridge structures bearing uniform weight between supports. J Struct Eng 140:04013093–1-04013093-7. doi:10.1061/(ASCE)ST.1493-541X.0000905
Cervera J (2010) Concebir y analizar estructuras. UPM, Madrid, http://oa.upm.es/189, versión 3.0. http://oa.upm.es/3691
Fernández Cabo JL (1998) Estructura: tamaño, forma y proporciõn. PhD thesis, Escuela Técnica Superior de Arquitectura, Madrid., http://oa.upm.es/14488/
Hemp W (1973) Optimum structures. Clarendon, Oxford
McConnel RE (1974) Least-weight framework for loads across span. J Eng Mech Div Proc ASCE 100:885–901
Michell AGM (1904) The limits of economy of materials in frame-structures. Philos Mag 8(47):589–597
Pichugin AV, Tyas A, Gilbert M (2012) On the optimality of Hemp’s arch with vertical hangers. Struct Multidiscip Optim 46:17–25. doi:10.1007/s00158-012-0769-5
Rozvany GIN, Prager W (1979) A new class of structural optimization problems: optimal archgrids. Comput Methods Appl Mech Eng 19(1):127–150
Sokół T (2014) Multiload–truss topology optimization using the adaptive ground structure approach. In: Łodygowski T, Rakowski J, Litewka P (eds) Recent Advances in Computational Mechanics. CRC Press, London , pp 9–16
Vázquez Espí M, Cervera Bravo J (2011) On the solution of the three forces problem and its application in optimal designing of a class of symmetric plane frameworks of least weight. Struct Multidisc Optim 44:723–727. doi:10.1007/s00158-011-0702-3
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Cervera Bravo, J., Vázquez Espí, C. & Vázquez Espí, M. On the layout of a least weight single span structure with uniform load. Struct Multidisc Optim 52, 1223–1228 (2015). https://doi.org/10.1007/s00158-015-1290-4
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00158-015-1290-4