Abstract
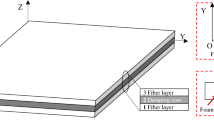
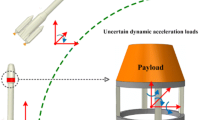
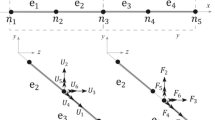
A new two-stage stochastic partial differential equation (PDE)-constrained optimization methodology is developed for the active vibration control of structures in the presence of uncertainties in mechanical loads. The methodology relies on the two-stage stochastic optimization formulation with an embedded first-order black-box PDE-constrained optimization procedure. The PDE-constrained optimization procedure utilizes a first-order active-set algorithm with a conjugate gradient method. The objective function is determined through solution of the governing PDEs and its gradient is computed using automatic differentiation with hyper-dual numbers. The developed optimization methodology is applied to the problem of post-impact vibration control (via applied electromagnetic field) of an electrically conductive carbon fiber reinforced composite plate subjected to an uncertain, or stochastic, impact load. The corresponding governing PDEs consist of a nonlinear coupled system of equations of motion and Maxwell’s equations. The conducted computational study shows that the obtained two-stage optimization solution allows for a significant suppression of vibrations caused by the randomized impact load in all impact load scenarios. Also, the effectiveness of the developed methodology is illustrated in the case of a deterministic impact load, where the two-stage strategy enables one to practically eliminate post-impact vibrations.






Similar content being viewed by others
References
Atkinson KE, Han W, Stewart DE (2009) Numerical solutions of ordinary differential equations. Wiley, New Jersey
Barakati A, Zhupanska OI (2012a) Analysis of the effects of a pulsed electromagnetic field on the dynamic response of electrically conductive composites. Appl Math Model 36:6072–6089
Barakati A, Zhupanska OI (2012b) Thermal and mechanical response of a carbon fiber reinforced composite to a transverse impact and in-plane pulsed electromagnetic loads. J Eng Mater Technol 134(3):031–004
Barakati A, Zhupanska OI (2013) Influence of the electric current waveform on the dynamic response of the electrified composites. Int J Mech Mater Des 9(1):11–20
Barakati A, Zhupanska OI (2014) Mechanical response of electrically conductive laminated composite plates in the presence of an electromagnetic field. Compos Struct 113:298–307
Bellman RE, Kalaba RE (1965) Modern analytic and computational methods in science and mathematics. Elsevier, New York
Birge JR, Louveaux F (2011) Introduction to Stochastic Programming, 2nd. Springer, New York
Chernikov D, Krokhmal P, Zhupanska OI (2015) Vibration mitigation in composite plates using an electromagnetic field. In: Proceedings of the 56th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics & Materials Conference, Kissimmee, FL, p to appear
Conti S, Held H, Pach M, Rumpf M, Schultz R (2009) Shape optimization under uncertainty & mdash;a stochastic programming perspective, vol 19, pp 1610–1632
Eringen AC (1989) Theory of electromagnetic elastic plates. Int J Eng Sci 27:363–375
Fike JA, Alonso JJ (2011) The development of hyper-dual numbers for exact second-derivative calculations. In: 49th AIAA Aerospace Sciences Meeting, vol 886
Gibson R (2010) A review of recent research on mechanics of multifunctional composite materials and structures. Compos Struct 92(12):2793–2810
Hager WW, Zhang H (2005) A new conjugate gradient method with guaranteed descent and an efficient line search. SIAM J Optim 16(1):170–192
Hager WW, Zhang H (2006) A new active set algorithm for box constrained optimization. SIAM J Optim 17(2):526–557
Hasanyan D, Librescu L, Ambur D (2006) Buckling and postbuckling of magnetoelastic flat plates carrying an electric current. Int J Solids Struct 43:4971–4996
Hasanyan DJ, Piliposyan GT (2001) Modelling and stability of magnetosoft ferromagnetic plates in a magnetic field. Proceedings of the Royal Society A 457:2063–2077
Herzog R, Kunisch K (2010) Algorithms for pde-constrained optimization. GAMM-Mitteilungen 33(2):163–176
Higuchi M, Kawamura R, Tanigawa Y (2007) Magneto-thermo-elastic stresses induced by a transient magnetic field in a conducting solid circular cylinder. Int J Solids Struct 44:5316–5335
Kall P, Mayer J (2005) Stochastic linear programming. Models theory, and computation. Springer
Kang BS, Choi WS, Park GJ (2001) Structural optimization under equivalent static loads transformed from dynamic loads based on displacement. Computers & Structures 79(2):145–154
Kantor IL, Solodovnikov AS (1989) Hypercomplex numbers: an elementary introduction to algebras. Springer-Verlag, New York
Martins JRRA, Sturdza P, Alonso JJ (2001) The connection between the complex-step derivative approximation and algorithmic differentiation. In: 39th Aerospace Sciences Meeting and Exhibit, vol 921, p 2001
Martins JRRA, Sturdza P, Alonso JJ (2003) The complex-step derivative approximation. ACM Trans Math Softw 29(3):245– 262
Maugin GA (1988) Continuum mechanics of electromagnetic solids. North-Holland, Amsterdam
Min S, Kikuchi N, Park YC, Kim S, Chang S (1999) Optimal topology design of structures under dynamic loads. Structural optimization 17(2–3):208–218
Moon FC (1984) Magnetosolid mechanics. Wiley, New York
Newmark NM (1959) A method of computation for structural dynamics. Journal of the Engineering Mechanics Division Proceedings of the ASCE 85:67–97
Piponi D (2004) Automatic differentiation, c++ templates, and photogrammetry. Journal of Graphics Tools 9(4):41–55
Prékopa A (1995) Stochastic programming. Kluwer Academic Publishers
Rall LB (1986) The arithmetic of differentiation. Math Mag 59(5):275–282
Rudnicki M (2002) Eigenvalue solutions for free motion of electroconductive plate in magnetic field. Int J Eng Sci 40:93–107
Shapiro A, Dentcheva D, Ruszczyński A (2009) Lectures on stochastic programming: modeling and theory. SIAM Philadelphia, PA
Squire W, Trapp G (1998) Using complex variables to estimate derivatives of real functions. SIAM Rev 40(1):110–112
Zhang X, Kang Z (2014) Dynamic topology optimization of piezoelectric structures with active control for reducing transient response. Comput Methods Appl Mech Eng 281:200–219
Zhupanska OI, Sierakowski RL (2007) Effects of an electromagnetic field on the mechanical response of composites. J Compos Mater 41(5):633–652
Zhupanska OI, Sierakowski RL (2011) Electro-thermo-mechanical coupling in carbon fiber polymer matrix composites. Acta Mech 218(3–4):219–232
Acknowledgments
Olesya Zhupanska and Dmitry Chernikov would like to acknowledge the support of DARPA, N66001-11-1-4133 (Disclaimer: Any opinions, findings, and conclusions or recommendations expressed in this publication are those of the authors and do not necessarily reflect the views of DARPA). Dmitry Chernikov is grateful for the support from the AFRL Mathematical Modeling and Optimization Institute during Summer 2013 and Summer 2014. Pavlo Krokhmal would like to acknowledge AFOSR grant FA9550-12-1-0142 and the U.S. Dept of Air Force grant FA8651-12-2-0010.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Chernikov, D., Krokhmal, P., Zhupanska, O.I. et al. A two-stage stochastic PDE-constrained optimization approach to vibration control of an electrically conductive composite plate subjected to mechanical and electromagnetic loads. Struct Multidisc Optim 52, 337–352 (2015). https://doi.org/10.1007/s00158-015-1238-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00158-015-1238-8