Skip to main content
SpringerLink
Log in

A framework of model validation and virtual product qualification with limited experimental data based on statistical inference

  • RESEARCH PAPER
  • Published:
Structural and Multidisciplinary Optimization Aims and scope Submit manuscript

Abstract

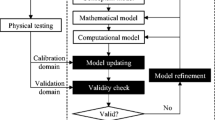
Virtual testing is a recent engineering development trend to design, evaluate, and test new engineered products. This research proposes a framework of virtual testing based on statistical inference for new product development comprising of three successive steps: (i) statistical model calibration, (ii) hypothesis test for validity check and (iii) virtual qualification. Statistical model calibration first improves the predictive capability of a computational model in a calibration domain. Next, the hypothesis test is performed with limited observed data to see if a calibrated model is sufficiently predictive for virtual testing of a new product design. An area metric and the u-pooling method are employed for the hypothesis test to measure the degree of mismatch between predicted and observed results while considering statistical uncertainty in the area metric due to the lack of experimental data. Once the calibrated model becomes valid, the virtual qualification process can be executed with a qualified model for new product developments. The qualification process builds a design decision matrix to aid in rational decision-making for product design alternatives. The effectiveness of the proposed framework is demonstrated through the case study of a tire tread block.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

Abbreviations

D :

critical value of area metric

e :

observation error

L :

likelihood function

l :

number of the known variables

p :

number of the unknown variables

q :

number of the controllable variables

U m :

area metric

y :

observed model

α :

significance level for a hypothesis test

β :

known model variable vector

δ :

prediction error

ζ :

operation variable vector

Θ :

hyper-parameter vector

θ :

unknown model variable vector

μ :

friction coefficient

υ :

pressure exponential parameter

φ :

contact pressure

ψ :

predicted model

References

  • AIAA, P.T.C (1998) Guide for the verification and validation of computational fluid dynamic simulations, AIAA Guide

  • ASME, P.T.C (2006) Guide for verification and validation in computational solid mechanics, ASME, New York

  • Babuska I, Oden JT (2004) Verification and validation in computational engineering and science: basic concepts. Comput Methods Appl Mech 193(36–38):4057–4066

  • Campbell K (2006) Statistical calibration of computer simulations. Reliab Eng Syst Saf 91(10–11):1358–1363

    Article  Google Scholar 

  • Chen W, Tsui K, Wang S (2008) A design-driven validation approach using Bayesian prediction models. J Mech Des 140(2):021101

    Article  Google Scholar 

  • Chen W, Baghdasaryan L, Buranathiti T, Cao J (2004) Model validation via uncertainty propagation. AIAA J 42:1406–1415

    Article  Google Scholar 

  • Cho JC, Jung BC (2007) Prediction of tread pattern wear by an explicit finite element model. Tire Sci Technol 35(4):276–299

    Article  Google Scholar 

  • Choi JH, Lee WH, Park JJ, Youn BD (2008) A study on robust design optimization of layered plate bonding process considering uncertainties. Struct Multidiscip Optim 35(6):531–540

  • Datta, B. N (2005) Finite element model updating and partial eigenvalue assignment in structural dynamics: recent developments on computational methods, Math Model Anal, pp. 15–27

  • Ferson S, Oberkampf WL, Ginzburg L (2008) Model validation and predictive capability for the thermal challenge problem. Comput Methods Appl Mech Eng 197(29–32):2408–2430

    Article  MATH  Google Scholar 

  • Higdon D, Nakhleh C, Gattiker J, Williams B (2008) A Bayesian calibration approach to the thermal problem. Comput Methods Appl Mech Eng 197(29–32):2431–2441

    Article  MATH  Google Scholar 

  • Hills RG, Truncano TG (2002) Statistical validation of engineering and scientific models: a maximum likelihood based metric, SAND2001–1783. Sandia National Labs, Albuquerque

    Book  Google Scholar 

  • Hofstetter K, Grohs C, Eberhardsteiner J, Mang HA (2006) Sliding behaviour of simplified tire tread patterns investigated by means of FEM. Comput Struct 84(17–18):1151–1163

    Article  Google Scholar 

  • Jung BC, Lee D, Youn BD (2009) Optimal design of constrained-layer damping structures considering material and operational condition variability. AIAA J 47(12):2985–2995

  • Kennedy MC, O’Hagan A (2002) Bayesian calibration of computer models. J R Stat Soc Ser B 63(3):425–464

    Article  MathSciNet  Google Scholar 

  • Kennedy MC, O’Hagan A (2001) Bayesian calibration of computer models. J R Stat Soc 63:425–464

    Article  MATH  MathSciNet  Google Scholar 

  • Liu F, Bayarri MJ, Berger JO, Paulo R, Sacks J (2008) A Bayesian analysis of the thermal challenge problem. Comput Methods Appl Mech Eng 197(29–32):2457–2466

    Article  MATH  Google Scholar 

  • Modarres, M., Kaminskiy, M., and Krivtsov, V (1999) Reliability engineering and risk analysis; a practical guide, CRC Press

  • Oberkampf WL, Trucano TG, Hirsch C (2004) Verification, validation, and predictive capability in computational engineering and physics. Appl Mech Rev 57:345

    Article  Google Scholar 

  • Oberkampf WL, Barone MF (2006) Measures of agreement between computation and experiment: validation metrics. J Comput Phys 217:5–36

    Article  MATH  Google Scholar 

  • Roache PJ (1998) Verification of codes and calculations. AIAA J 36(5):696–702

    Article  Google Scholar 

  • Thacker BH, Doebling SW, Hemez FM, Anderson MC, Pepin JE, Rodriguez EA (2004) Concepts of model verification and validation, Technical report, LA-14167. Los Alamos National Lab, Los Alamos

    Book  Google Scholar 

  • Trucano TG, Swiler LP, Igusa T, Oberkampf WL, Pilch M (2006) Calibration, validation, and sensitivity analysis: what’s what. Reliab Eng Syst Saf 91(10–11):1331–1357

    Article  Google Scholar 

  • Xi Z, Hu C, Youn BD (2012) A comparative study of probability estimation methods for reliability analysis. Struct Multidiscip Optim 45(1):33–52

  • Xiong Y, Chen W, Tsui K, Apley DW (2009) A better understanding of model updating strategies in validating engineering models. Comput Methods Appl Mech Eng 198(15–16):1327–1337

    Article  MATH  Google Scholar 

  • Youn BD, Xi Z, Wang P (2008) Eigenvector dimension reduction (EDR) method for sensitivity-free probability analysis. Struct Multidiscip Optim 37(1):13–28

    Article  MATH  MathSciNet  Google Scholar 

  • Youn BD, Jung BC, Xi ZM, Kim SB, Lee WR (2011) A hierarchical framework for statistical model calibration in engineering product development. Comput Methods Appl Mech Eng 200:1421–1431. doi:10.1016/j.cma.2010.12.012

  • Wang P, Youn, B. D., Xi Z., Kloess A. (2009) Bayesian reliability analysis with evolving, insufficient, and subjective data sets. J Mech Des 131(11):111008

  • Zhang R, Mahadevan S (2003) Bayesian methodology for reliability model acceptance. Reliab Eng Syst Saf 80:95–103

    Article  Google Scholar 

Download references

Acknowledgments

This work was partially supported by a grant from the Energy Technology Development Program (2010101010027B) and International Collaborative R&D Program (0420-2011-0161) of Korea Institute of Energy Technology Evaluation and Planning (KETEP), funded by the Korean government’s Ministry of Knowledge Economy, the National Research Foundation of Korea (NRF) grant (No. 2011–0022051) funded by the Korea government, the Basic Research Project of Korea Institute of Machinery and Materials (Project Code : SC1000) supported by a grant from Korea Research Council for Industrial Science & Technology, and the Institute of Advanced Machinery and Design at Seoul National University (SNU-IAMD).

Author information

Authors and Affiliations

  1. Department of System Dynamics, Korea Institute of Machinery and Materials, Daejeon, 305-343, South Korea

    Byung C. Jung

  2. Department of Mechanical and Aerospace Engineering, Seoul National University, Seoul, 151-742, South Korea

    Jungho Park, Hyunseok Oh, Jisun Kim & Byeng D. Youn

Authors
  1. Byung C. Jung
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jungho Park
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Hyunseok Oh
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Jisun Kim
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Byeng D. Youn
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Byeng D. Youn.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jung, B.C., Park, J., Oh, H. et al. A framework of model validation and virtual product qualification with limited experimental data based on statistical inference. Struct Multidisc Optim 51, 573–583 (2015). https://doi.org/10.1007/s00158-014-1155-2

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00158-014-1155-2

Keywords

Search

Navigation