Skip to main content
SpringerLink
Log in

Topology optimization using an explicit interface representation

  • RESEARCH PAPER
  • Published:
Structural and Multidisciplinary Optimization Aims and scope Submit manuscript

Abstract

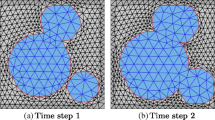
We introduce the Deformable Simplicial Complex method to topology optimization as a way to represent the interface explicitly yet being able to handle topology changes. Topology changes are handled by a series of mesh operations, which also ensures a well-formed mesh. The same mesh is therefore used for both finite element calculations and shape representation. In addition, the approach unifies shape and topology optimization in a complementary optimization strategy. The shape is optimized on the basis of the gradient-based optimization algorithm MMA whereas holes are introduced using topological derivatives. The presented method is tested on two standard minimum compliance problems which demonstrates that it is both simple to apply, robust and efficient.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

Notes

  1. Presented at the 10th World Congress on Structural and Multidisciplinary Optimization in 2013.

  2. CHOLMOD is the default solver for sparse symmetric positive definite linear systems in MATLAB.

References

  • Allaire G, Jouve F, Toader AM (2004) Structural optimization using sensitivity analysis and a level-set method. J Comput Phys 194(1):363–393

    Article  MATH  MathSciNet  Google Scholar 

  • Allaire G, Dapogny C, Frey P (2011) Topology and geometry optimization of elastic structures by exact deformation of simplicial mesh. Compt Rendus Math 349(17–18):999–1003

    Article  MATH  MathSciNet  Google Scholar 

  • Allaire G, Dapogny C, Frey P (2013) A mesh evolution algorithm based on the level set method for geometry and topology optimization. Struct Multidiscip Optim 1–5

  • Ambrosio L, Buttazzo G (1993) An optimal design problem with perimeter penalization. Calc Var 1(1):55–69

    Article  MATH  MathSciNet  Google Scholar 

  • Amstutz S (2010) A penalty method for topology optimization subject to a pointwise state constraint. ESAIM: Control Optim Calc Var 16:523–544

    Article  MATH  MathSciNet  Google Scholar 

  • Arnout S, Firl M, Bletzinger KU (2012) Parameter free shape and thickness optimisation considering stress response. Struct Multidiscip Optim 45(6):801–814

    Article  MATH  Google Scholar 

  • Bærentzen JA, Gravesen J, Anton F, Aanæs H (2012) Guide to computational geometry processing: foundations, algorithms, and methods. Springer, London

    Book  Google Scholar 

  • Bærentzen JA, Revall Frisvad J, Aanæs H (2013) Geometry and linear algebra (GEL) library. http://www2.imm.dtu.dk/projects/GEL/

  • Bendsøe MP, Sigmund O (1999) Material interpolation schemes in topology optimization. Arch Appl Mech 69(9–10):635–654

    Google Scholar 

  • Bletzinger KU, Maute K (1997) Towards generalized shape and topology optimization. Eng Optim 29(1–4):201–216

    Article  Google Scholar 

  • Céa J, Garreau S, Guillaume P, Masmoudi M (2000) The shape and topological optimizations connection. Comput Methods Appl Mech Eng 188(4):713–726

    Article  MATH  Google Scholar 

  • Chen Y, Davis TA, Hager WW, Rajamanickam S (2008) Algorithm 887: cholmod, supernodal sparse cholesky factorization and upyear/downyear. ACM Trans Math Softw 35(3):22:1–22:14

    Article  MathSciNet  Google Scholar 

  • Cheng S, Dey T, Shewchuk J (2012) Delaunay mesh generation. Chapman & Hall/CRC Computer and Information Science. CRC Press INC, Boca Raton

    Google Scholar 

  • Davis TA, Hager WW, Duff IS (2013) Suite sparse. http://www.cise.ufl.edu/research/sparse/SuiteSparse/

  • Ding Y (1986) Shape optimization of structures: a literature survey. Comput Struct 24(6):985–1004

    Article  MATH  Google Scholar 

  • Eschenauer HA, Kobelev VV, Schumacher A (1994) Bubble method for topology and shape optimization of structures. Struct Multidiscip Optim 8:42–51

    Article  Google Scholar 

  • Feijóo RA, Novotny AA, Taroco E, Padra C (2003) The topological derivative for the poisson’s problem. Math Model Methods Appl Sci 13(12):1825–1844

    Article  MATH  Google Scholar 

  • Ha SH, Cho S (2008) Level set based topological shape optimization of geometrically nonlinear structures using unstructured mesh. Comput Struct 86(13–14):1447–1455

    Article  Google Scholar 

  • Kim DH, Lee SB, Kwank BM, Kim HG, Lowther D (2008) Smooth boundary topology optimization for electrostatic problems through the combination of shape and topological design sensitivities. IEEE Trans Magn 44(6):1002–1005

    Article  Google Scholar 

  • Le C, Bruns T, Tortorelli D (2011) A gradient-based, parameter-free approach to shape optimization. Comput Methods Appl Mech Eng 200(9–12):985–996

    Article  MATH  MathSciNet  Google Scholar 

  • Maute K, Ramm E (1995) Adaptive topology optimization. Struct Optim 10:100–112

    Article  Google Scholar 

  • Misztal MK, Bærentzen JA (2012) Topology adaptive interface tracking using the deformable simplicial complex. ACM Trans Graph 31(3):24

    Article  Google Scholar 

  • Misztal MK, Bridson R, Erleben K, Bærentzen JA, Anton F (2010) Optimization-based fluid simulation on unstructured meshes. In: 7th workshop on virtual reality interaction and physical simulation VRIPHYS, p 10

  • Misztal MK, Erleben K, Bargtei A, Fursund J, Christensen BB, Bærentzen JA, Bridson R (2012) Multiphase flow of immiscible fluids on unstructured moving meshes. In: Proceedings of the ACM SIGGRAPH/Eurographics Symposium on Computer Animation, Eurographics Association, Aire-la-Ville, Switzerland, SCA ’12, pp 97–106

  • Mohammadi B, Pironneau FO (2001) Applied shape optimization for fluids. Oxford University Press, Oxford

    MATH  Google Scholar 

  • Osher SJ, Fedkiw RP (2002) Level set methods and dynamic implicit surfaces, 1st edn. Springer, New York

    Google Scholar 

  • Sokolowski J, Zochowski A (1999) On the topological derivative in shape optimization. SIAM J Control Optim 37(4):1251–1272

    Article  MATH  MathSciNet  Google Scholar 

  • Sokołowski J, Zolésio J (1992) Introduction to shape optimization: shape sensitivity analysis. Springer series in computational mathematics. Springer-Verlag, New York

    Book  Google Scholar 

  • Svanberg K (1987) The method of moving asymptotes—a new method for structural optimization. Int J Numer Methods Eng 24(2):359–373

    Article  MATH  MathSciNet  Google Scholar 

  • Wang M, Wang X, Guo D (2003) A level set method for structural topology optimization. Comput Methods Appl Mech Eng 192(1):227–246

    Article  MATH  Google Scholar 

  • Xia Q, Shi T, Liu S, Wang MY (2012) A level set solution to the stress-based structural shape and topology optimization. Comput Struct 90–91:55–64

    Article  Google Scholar 

  • Yamasaki S, Nomura T, Kawamoto A, Sato K, Nishiwaki S (2011) A level set-based topology optimization method targeting metallic waveguide design problems. Int J Numer Methods Eng 87(9):844–868

    Article  MATH  MathSciNet  Google Scholar 

Download references

Acknowledgments

The authors appreciate the support from the Villum Foundation through the grant: “NextTop”

Author information

Authors and Affiliations

  1. Department of Applied Mathematics and Computer Science, Technical University of Denmark, Matematiktorvet, B.303B, 2800 Kgs., Lyngby, Denmark

    Asger Nyman Christiansen, Morten Nobel-Jørgensen & Jakob Andreas Bærentzen

  2. Department of Mechanical Engineering, Technical University of Denmark, Nils Koppels Allé, B.404, 2800 Kgs, Lyngby, Denmark

    Niels Aage & Ole Sigmund

Authors
  1. Asger Nyman Christiansen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Morten Nobel-Jørgensen
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Niels Aage
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Ole Sigmund
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Jakob Andreas Bærentzen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Asger Nyman Christiansen.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Christiansen, A.N., Nobel-Jørgensen, M., Aage, N. et al. Topology optimization using an explicit interface representation. Struct Multidisc Optim 49, 387–399 (2014). https://doi.org/10.1007/s00158-013-0983-9

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00158-013-0983-9

Keywords

Search

Navigation