Skip to main content
SpringerLink
Log in

Parametric structural optimization with dynamic knot RBFs and partition of unity method

  • Research Paper
  • Published:
Structural and Multidisciplinary Optimization Aims and scope Submit manuscript

Abstract

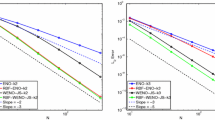
An efficient algorithm is presented for solving optimization problem of geometrical domains in which elliptic boundary value problems are defined. The surface of the domain is implicitly described through a level set function and the moving boundary is determined by the time-dependent dynamic knots of the radial basis functions (RBFs). A method of Partition of Unity (POU) is leveraged to calculate the solution, which divides the domain into some smaller overlapping local sub-domains and reconstructs them into the global surface with less numerical cost. Apart from the convergence properties, numerical results are given and discussed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  • Allaire G, Jouve F, Toader A-M (2004) Structural optimization using sensitivity analysis and a level-set method. J Comput Phys 194(1):363–393

    Article  MathSciNet  MATH  Google Scholar 

  • Allaire G, Jouve F (2008) Minimum stress optimal design with the level set method. Eng Anal Bound Elem 32(11):909–918

    Article  MATH  Google Scholar 

  • Bendsøe MP (1989) Optimal shape design as a material distribution problem. Struct Multidisc Optim 1:193–202

    Article  Google Scholar 

  • Bendsøe MP, Kikuchi N (1988) Generating optimal topologies in structural design using a homogenization method. Comput Methods Appl Mech Eng 71:197–224

    Article  Google Scholar 

  • Bendsøe MP, Sigmund O (2003) Topology optimization: theory, methods and applications, 2nd edn. Springer, Berlin

    Google Scholar 

  • Buhmann MD (2004) Radial basis functions: theory and implementations. In: Cambridge monographs on applied and computational mathematics, vol 12. Cambridge University Press, New York

    Google Scholar 

  • Cheng AD, Golberg MA, Kansa EJ, Zammito G (2003) Exponential convergence and h-c multiquadric collection method for partial differential equations. Numer Methods Partial Differ Equ 19:571–594

    Article  MathSciNet  MATH  Google Scholar 

  • Ho HS, Lui BFY, Wang MY (2011) Parametric shape and topology optimization with radial basis functions and partition of unity method. Optim Methods Softw 26(4–5):533–553

    Article  MathSciNet  MATH  Google Scholar 

  • Griebel M, Schweitzer MA (2000) A particle-partition of unity method for the solution of elliptic, parabolic, and hyperbolic pdes. SIAM J Sci Comput 22:853–890

    Article  MathSciNet  MATH  Google Scholar 

  • Lui BFY, Wang MY, Xia Q (2007) Parametric shape and topology optimization via radial basis functions, partition of unity and level set method. In: Proceedings of 5th China–Japan–Korea joint symposium on optimization of structural and mechanical systems. Jeju, Korea

    Google Scholar 

  • Luo Z, Wang MY, Wang SY, Wei P (2007) A level set-based parameterization method for structural shape and topology optimization. Int J Numer Methods Eng 76(1):1–26

    Article  MathSciNet  Google Scholar 

  • Ohtake Y, Belyaev A, Alexa M, Turk G, Seidel HP (2003) Multi-level partition of unity implicits. In: Proceedings of ACM SIGGRAPH 2007 (SESSION: Surfaces), pp 463–470

  • Rozvany GIN, Zhou M, Birker T (1992) Generalized shape optimization without homogenization. Struct Multidisc Optim 4(3–4):250–252

    Google Scholar 

  • Tobor I, Reuter P, Schlick C (2004a) Efficient reconstruction of large scattered geometric datasets using the partition of unity and radial basis functions. J WSCG (12):467–474

  • Tobor I, Reuter P, Schlick C (2004b) Multi-scale reconstruction of implicit surfaces with attributes from large unorganized point sets. In: Proceedings of shape modeling applications, pp 19–30

  • Wang SY, Wang MY (2006) Radial basis functions and level set method for structural topology optimization. Int J Numer Methods Eng 65:2060–2090

    Article  MATH  Google Scholar 

  • Wang MY, Wang XM, Guo DM (2003) A level set method for structural topology optimization. Comput Methods Appl Mech Eng 192:227–246

    Article  MATH  Google Scholar 

  • Wei P, Wang MY (2006) Parametric structural shape and topology optimization method with radial basis functions and level-set method. In: Proceedings of IDETC/CIE, pp 19–30

  • Wu X, Wang MY, Xia Q (2005) Implicit fitting and smoothing using radial basis functions with partition of unity. In: Proceedings of the ninth international conference (2005) on computer aided design and computer graphics, pp 139–148

  • Xie YM, Steven GP (1993) A simple evolution procedure for structural optimization. Comput Struct 49(5):885–896

    Article  Google Scholar 

  • Xie YM, Steven GP (1997) Evolutionary structural optimization. Springer, New York

    Book  MATH  Google Scholar 

  • Xing XH, Wang MY, Lui BFY (2007) Parametric shape and topology optimization with moving knots radial basis functions and level set methods. In: Proceedings of the 7th WCSMO, pp 1928–1936

Download references

Acknowledgement

This research work is supported by the Research Grants Council of Hong Kong SAR (Project No. CUHK417309).

Author information

Authors and Affiliations

  1. Department of Electrical Engineering, The Hong Kong Polytechnic University, Hunghom, Kowloon, Hong Kong

    Hon Shan Ho

  2. Department of Mechanical and Automation Engineering, The Chinese University of Hong Kong, Shatin, NT, Hong Kong

    Michael Yu Wang & Mingdong Zhou

Authors
  1. Hon Shan Ho
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Michael Yu Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Mingdong Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Michael Yu Wang.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Ho, H.S., Wang, M.Y. & Zhou, M. Parametric structural optimization with dynamic knot RBFs and partition of unity method. Struct Multidisc Optim 47, 353–365 (2013). https://doi.org/10.1007/s00158-012-0848-7

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00158-012-0848-7

Keywords

Search

Navigation