Skip to main content
SpringerLink
Log in

A simple and effective inverse projection scheme for void distribution control in topology optimization

  • RESEARCH PAPER
  • Published:
Structural and Multidisciplinary Optimization Aims and scope Submit manuscript

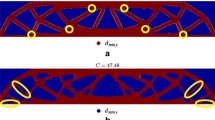
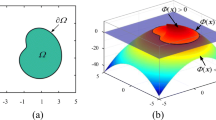
Abstract

The ability to control both the minimum size of holes and the minimum size of structural members are essential requirements in the topology optimization design process for manufacturing. This paper addresses both requirements by means of a unified approach involving mesh-independent projection techniques. An inverse projection is developed to control the minimum hole size while a standard direct projection scheme is used to control the minimum length of structural members. In addition, a heuristic scheme combining both contrasting requirements simultaneously is discussed. Two topology optimization implementations are contributed: one in which the projection (either inverse or direct) is used at each iteration; and the other in which a two-phase scheme is explored. In the first phase, the compliance minimization is carried out without any projection until convergence. In the second phase, the chosen projection scheme is applied iteratively until a solution is obtained while satisfying either the minimum member size or minimum hole size. Examples demonstrate the various features of the projection-based techniques presented.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Bendsøe MP (1989) Optimal shape design as a material distribution problem. Struct Optim 1(4):193–202

    Article  Google Scholar 

  • Bendsøe MP, Sigmund O (2003) Topology optimization: theory, methods and applications. Springer, New York

    Google Scholar 

  • Borrvall T, Petersson J (2001) Topology optimization using regularized intermediate density control. Comput Methods Appl Mech Eng 190(37):4911–4928

    Article  MATH  MathSciNet  Google Scholar 

  • Bourdin B (2001) Filters in topology optimization. Int J Numer Methods Eng 50(9):2143–2158

    Article  MATH  MathSciNet  Google Scholar 

  • Carbonari RC, Silva ECN, Paulino GH (2007) Topology optimization design of functionally graded bimorph-type piezoeletric actuators. Smart Mater Struc 16(6):2605–2620

    Article  Google Scholar 

  • Carbonari RC, Silva ECN, Paulino GH (2009) Multi-actuated functionally graded piezoelectric micro-tools design: a multiphysics topology optimization approach. Int J Numer Methods Eng. doi:10.1002/nme.2403

  • Chang K-H, Tang P-S (2001) Integration of design and manufacturing for structural shape optimization. Adv Eng Softw 32(7):555–567

    Article  MATH  Google Scholar 

  • Guest JK (2009) Imposing maximum length scale in topology optimization. Struct Multidisc Optim. doi:10.1007/s00158-008-0250-7

  • Guest JK, Prévost JH, Belytschko T (2004) Achieving minimum length scale in topology optimization using nodal design variables and projection functions. Int J Numer Methods Eng 61(2):238–254

    Article  MATH  Google Scholar 

  • Guo X, Gu YX (2004) A new density-stiffness interpolation scheme for topology optimization of continuum structures. Eng Comput 21(1):9–22

    Article  MATH  Google Scholar 

  • Ishii K, Aomura S (2004) Topology optimization for the extruded three dimensional structure with constant cross section. JSME Int J, Series A, 47(2):198–206

    Article  Google Scholar 

  • Matsui K, Terada K (2004) Continuous approximation for material distribution for topology optimization. Int J Numer Methods Eng 59(14):1925–1944

    Article  MATH  MathSciNet  Google Scholar 

  • Nitsopoulos I, Lauber B (2007) Overview on optimization methods, FE-DESIGN GmbH, TOSCA Structure. ANSA and META International Congress, June 14–15,2002. http://www.fe-design.com

  • Rozvany GIN (2001a) Topology optimization in structural mechanics. Editorial. Struct Multidisc Optim 21(2):89

    Article  Google Scholar 

  • Rozvany GIN (2001b) Aims, scope, methods, history and unified terminology of computer-aided topology optimization in structural mechanics. Struct Multidisc Optim 21(2):90–108

    Article  Google Scholar 

  • Sigmund O (1997) On the design of compliant mechanisms using topology optimization. Mechan Struct Mach 25(4):493–524

    Article  Google Scholar 

  • Sigmund O (2001) Design of multiphysics actuators using topology optimization—part II: two-material structures. Comput Methods Appl Mech Eng 190(49–50):6605–6627

    Article  Google Scholar 

  • Sigmund O (2007) Morphology-based black and white filters for topology optimization. Struct Multidisc Optim 33(4–5):401–424

    Article  Google Scholar 

  • Wang MY, Wang S (2005) Bilateral filtering for structural topology optimization. Int J Numer Methods Eng 63(13):1911–1938

    Article  MATH  Google Scholar 

  • Zhou M, Rozvany GIN (1991) The COC algorithm, part II: topological, geometry and generalized shape optimization. Comput Methods Appl Mech Eng 89(1):197–224

    Article  Google Scholar 

  • Zhou M, Shyy YK, Thomas HL (2001) Checkerboard and minimum member size control in topology optimization. Struct Multidisc Optim 21(2):152–158

    Article  Google Scholar 

  • Zuo K-T, Chen L-P, Zhang Y-Q, Yang J (2006) Manufacturing- and machining-based topology optimization. Int J Adv Manuf Technol 27(5–6):531–536

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Escola de Engenharia Civil, Universidade Federal de Goiás, Av. Universitária, 1488, Qd. 86, Setor Universitário, Goiânia, GO, 74605-220, Brazil

    S. R. M. Almeida

  2. Department of Civil and Environmental Engineering, University of Illinois at Urbana-Champaign, Newmark Laboratory, 205 North Mathews Avenue, Urbana, IL, 61801, USA

    G. H. Paulino

  3. Department of Mechatronics and Mechanical Systems Engineering, Escola Politécnica da Universidade de São Paulo, Av. Professor Mello Moraes, 2231, São Paulo, SP, 05508-900, Brazil

    E. C. N. Silva

Authors
  1. S. R. M. Almeida
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. G. H. Paulino
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. E. C. N. Silva
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to G. H. Paulino.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Almeida, S.R.M., Paulino, G.H. & Silva, E.C.N. A simple and effective inverse projection scheme for void distribution control in topology optimization. Struct Multidisc Optim 39, 359–371 (2009). https://doi.org/10.1007/s00158-008-0332-6

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00158-008-0332-6

Keywords

Search

Navigation