Abstract
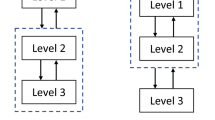
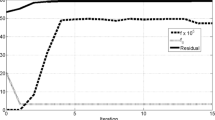
Several decomposition methods have been proposed for the distributed optimal design of quasi-separable problems encountered in Multidisciplinary Design Optimization (MDO). Some of these methods are known to have numerical convergence difficulties that can be explained theoretically. We propose a new decomposition algorithm for quasi-separable MDO problems. In particular, we propose a decomposed problem formulation based on the augmented Lagrangian penalty function and the block coordinate descent algorithm. The proposed solution algorithm consists of inner and outer loops. In the outer loop, the augmented Lagrangian penalty parameters are updated. In the inner loop, our method alternates between solving an optimization master problem and solving disciplinary optimization subproblems. The coordinating master problem can be solved analytically; the disciplinary subproblems can be solved using commonly available gradient-based optimization algorithms. The augmented Lagrangian decomposition method is derived such that existing proofs can be used to show convergence of the decomposition algorithm to Karush–Kuhn–Tucker points of the original problem under mild assumptions. We investigate the numerical performance of the proposed method on two example problems.
Similar content being viewed by others
References
Alexandrov NM, Lewis RM (2002) Analytical and computational aspects of collaborative optimization for multidisciplinary design. AIAA J 40(2):301–309
Allison JT, Kokkalaras M, Zawislak MR, Papalambros PY (2005) On the use of analytical target cascading and collaborative optimization for complex system design. In: Proceedings of the 6th world congress on structural and multidisciplinary optimization, Rio de Janeiro, Brazil
Arora JS, Chahande AI, Paeng J (1991) Multiplier methods for engineering optimization. Int J Numer Methods Eng 32(7):1485–1525
Balling RJ, Sobieszczanski-Sobieski J (1996) Optimization of coupled systems: a critical overview of approaches. AIAA J 34(1):6–17
Bazaraa MS, Sherali HD, Shetty CM (1993) Nonlinear programming: theory and algorithms. Wiley, New York
Bertsekas DP (1982) Constrained optimization and lagrange multiplier methods. Academic, New York
Bertsekas DP (2003) Nonlinear programming, 2nd edn. Athena Scientific, Belmont, Massachusetts (2nd printing)
Bertsekas DP, Tsitsiklis JN (1989) Parallel and distributed computation. Prentice-Hall, Englewood Cliffs, NJ
Bezdek JC, Hathaway R (2002) Some notes on alternating optimization. Lect Notes Comput Sci 2275:288–300
Braun RD (1996) Collaborative optimization: an architecture for large-scale distributed design. Ph.D. thesis, Stanford University
Braun RD, Moore AA, Kroo IM (1997) Collaborative approach to launch vehicle design. J Spacecr Rockets 34:478–486
Cramer EJ, Dennis JE, Frank PD, Lewis RM, Shubin GR (1994) Problem formulation for multidisciplinary optimization. SIAM J Optim 4(4):754–776
DeMiguel AV, Murray W (2000) An analysis of collaborative optimization methods. In: Eight AIAA/USAF/NASA/ISSMO symposium on multidisciplinary analysis and optimization, AIAA Paper 00-4720
DeMiguel AV, Murray W (2006) A local convergence analysis of bilevel decomposition algorithms. Optim Eng 7:99–133
Fortin M, Glowinski R (1983) Augmented lagrangian methods: application to the numerical solution of boundary-value problems. North-Holland, Amsterdam, the Netherlands
Gill PE, Murray W, Wright MH (1981) Practical optimization. Academic, London, UK
Golinski J (1970) Optimal synthesis problems solved by means of nonlinear programming and random methods. J Mech 5:287–309
Haftka RT, Watson LT (2005) Multidisciplinary design optimization with quasiseparable subsystems. Optim Eng 6:9–20
Holmström K, Göran AO, Edvall MM (2004) User’s guide for TOMLAB 4.2. Tomlab Optimization Inc., San Diego CA. http://tomlab.biz (website date of access: 23 November 2006)
Kim HM (2001) Target cascading in optimal system design. Ph.D. thesis, University of Michigan
Kokkolaras M, Fellini R, Kim HM, Michelena NF, Papalambros PY (2002) Extension of the target cascading formulation to the design of product families. Struct Multidiscipl Optim 24(4):293–301
Liu B, Haftka RT, Watson LT (2004) Global–local structural optimization using response surfaces of local optimization margins. Struct Multidiscipl Optim 27(5):352–359
Michalek JJ, Papalambros PY (2005a) An efficient weighting update method to achieve acceptable inconsistency deviation in analytical target cascading. ASME J Mech Des 127:206–214
Michalek JJ, Papalambros PY (2005b) Technical brief: weights, norms, and notation in analytical target cascading. ASME J Mech Des 127:499–501
Michelena N, Kim HM, Papalambros PY (1999) A system partitioning and optimization approach to target cascading. In: Proceedings of the 12th international conference on engineering design, Munich, Germany
Michelena NF, Park H, Papalambros PY (2003) Convergence properties of analytical target cascading. AIAA J 41(5):897–905
Sobieski IP, Kroo I (2000) Collaborative optimization using response surface estimation. AIAA J 38(10):1931–1938
Sobieszczanski-Sobieski J (1988) Optimization by decomposition: a step from hierarchic to non-hierarchic systems. In: 2nd NASA Air Force symposium on recent advances in multidisciplinary analysis and optimization, Hampton, Virginia, NASA-CP 3031
Sobieszczanski-Sobieski J, Agte JS, Sandusky Jr RR (2000) Bilevel integrated system synthesis. AIAA J 38(1):164–172
Sobieszczanski-Sobieski J, Altus TD, Phillips M, Sandusky Jr RR (2003) Bilevel integrated system synthesis for concurrent and distributed processing. AIAA J 41(10):1996–2003
Tosserams S (2004) Analytical target cascading: Convergence improvement by subproblem post-optimality sensitivities. Master’s thesis, Eindhoven University of Technology, The Netherlands, SE-420389
Tosserams S, Etman LFP, Papalambros PY, Rooda JE (2006) An augmented lagrangian relaxation for analytical target cascading using the alternating direction method of multipliers. Struct Multidiscipl Optim 31(3):176–189. DOI 10.1007/s00158-005-0579-0
Tzevelekos N, Kokkolaras M, Papalambros PY, Hulshof MF, Etman LFP, Rooda JE (2003) An empirical local convergence study of alternative coordination schemes in analytical target cascading. In: Proceedings of the 5th world congress on structural and multidisciplinary optimization, Lido di Jesolo, Venice, Italy
Wagner TC (1993) A general decomposition methodology for optimal system design. Ph.D. thesis, Univerisy of Michigan, Ann Arbor
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Tosserams, S., Etman, L.F.P. & Rooda, J.E. An augmented Lagrangian decomposition method for quasi-separable problems in MDO. Struct Multidisc Optim 34, 211–227 (2007). https://doi.org/10.1007/s00158-006-0077-z
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00158-006-0077-z